18.1平行四边形 同步训练题(Word版 含答案)
文档属性
| 名称 | 18.1平行四边形 同步训练题(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 424.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 00:00:00 | ||
图片预览



文档简介
18.1平行四边形 同步训练题
1.已知在四边形ABCD中,AB=3,CD=5,M,N分别是AD,BC的中点,则线段MN的取值范围是( )
A.1<MN<4 B.1<MN≤4 C.2<MN<8 D.2<MN≤8
2.如图,?ABCD的周长为16cm,AB≠AD,AC和BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长是( )
A.10cm B.8m C.6m D.4cm
3.如图,在平行四边形ABCD中,E,F是对角线BD上不同的两点,连接AE,CE,AF,CF.下列条件中,不能得出四边形AECF一定是平行四边形的为( )
A.BE=DF B.AE=CF C.AF∥CE D.∠BAE=∠DCF
4.如图,在△ABC中,AD是角平分线,AE是中线,CF⊥AD于点F,AC=5,AB=13,则EF的长为( )
A. B. C.3 D.4
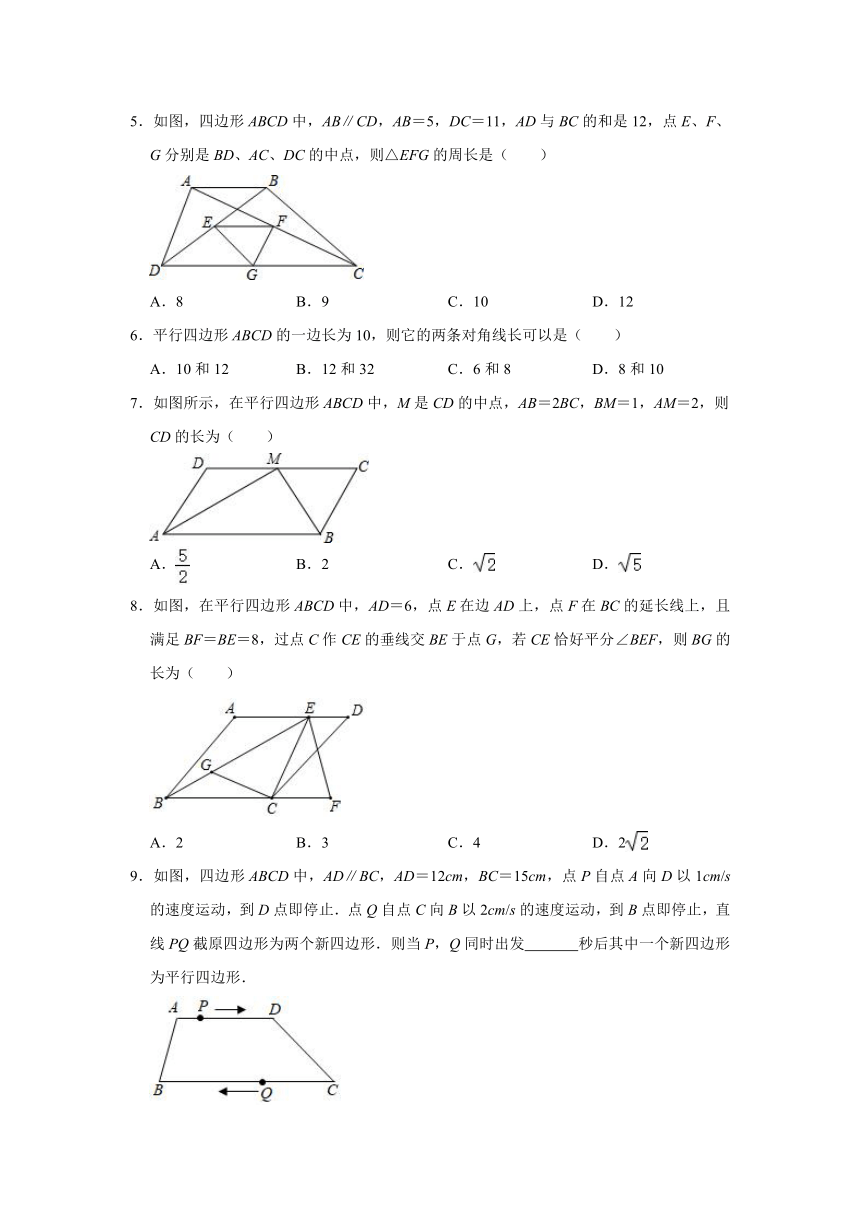
5.如图,四边形ABCD中,AB∥CD,AB=5,DC=11,AD与BC的和是12,点E、F、G分别是BD、AC、DC的中点,则△EFG的周长是( )
A.8 B.9 C.10 D.12
6.平行四边形ABCD的一边长为10,则它的两条对角线长可以是( )
A.10和12 B.12和32 C.6和8 D.8和10
7.如图所示,在平行四边形ABCD中,M是CD的中点,AB=2BC,BM=1,AM=2,则CD的长为( )
A. B.2 C. D.
8.如图,在平行四边形ABCD中,AD=6,点E在边AD上,点F在BC的延长线上,且满足BF=BE=8,过点C作CE的垂线交BE于点G,若CE恰好平分∠BEF,则BG的长为( )
A.2 B.3 C.4 D.2
9.如图,四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截原四边形为两个新四边形.则当P,Q同时出发 秒后其中一个新四边形为平行四边形.
10.如图所示,在平行四边形ABCD中,AB=3,BC=4,∠B=60°,E是BC的中点,EF⊥AB于点F,则△DEF的面积为 平方单位.
11.如图,在平行四边形ABCD中,BE平分∠ABC,CF⊥BE,连接AE,G是AB的中点,连接GF,若AE=4,则GF= .
12.如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为 .
13.平行四边形ABCD中,∠ABC的平分线将AD边分成的两部分的长分别为2和3,则平行四边形ABCD的周长是
.
14.如图,点D、E分别为△ABC的边AB、AC的中点,同时,点F在DE上,且∠AFB=90°,已知AB=5,BC=8,那么EF的长为 .
15.在Rt△ABC中,∠ACB=90°,AE,BD是角平分线,CM⊥BD于M,CN⊥AE于N,若AC=6,BC=8,则MN= .
16.已知A(1,1),B(4,3),C(6,﹣2),在平面直角坐标找一点D,使以A、B、C、D四点的四边形为平行四边形,则D点的坐标是 .
17.如图,平行四边形ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,CF=1,则AB的长是 .
18.如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于G,AB=6,则AG= .
19.如图,△ABC中,AB=7,AC=11,AD平分∠BAC,BD⊥AD,E是BC的中点,那么DE=
20.如图,四边形ABCD中,AD∥BC,AD=8cm,BC=12cm,M是BC上一点,且BM=9cm,点E从点A出发以1cm/s的速度向点D运动,点F从点C出发,以3cm/s的速度向点B运动,当其中一点到达终点,另一点也随之停止,设运动时间为t,则当以A、M、E、F为顶点的四边形是平行四边形时,t=
21.如图,在?ABCD中,E为BC边上一点,且AB=AE.
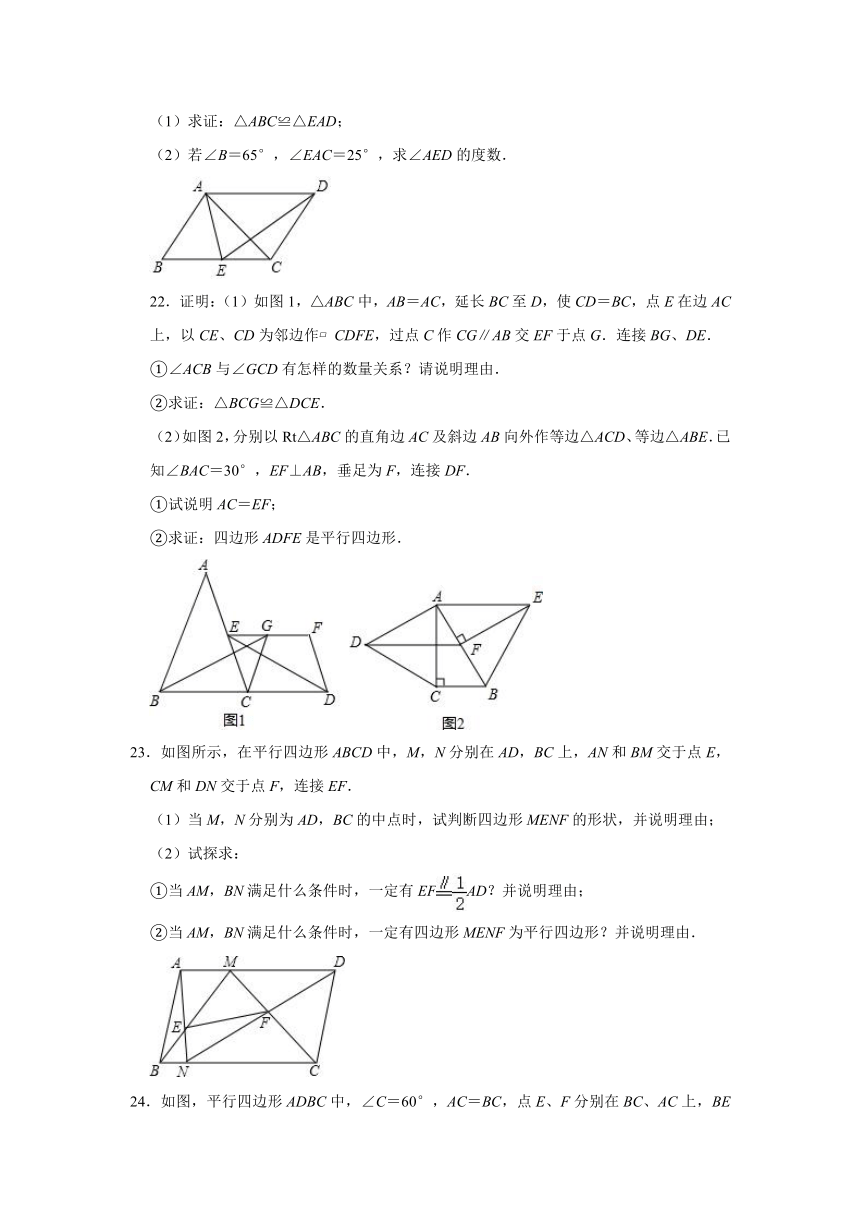
(1)求证:△ABC≌△EAD;
(2)若∠B=65°,∠EAC=25°,求∠AED的度数.
22.证明:(1)如图1,△ABC中,AB=AC,延长BC至D,使CD=BC,点E在边AC上,以CE、CD为邻边作?CDFE,过点C作CG∥AB交EF于点G.连接BG、DE.
①∠ACB与∠GCD有怎样的数量关系?请说明理由.
②求证:△BCG≌△DCE.
(2)如图2,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
①试说明AC=EF;
②求证:四边形ADFE是平行四边形.
23.如图所示,在平行四边形ABCD中,M,N分别在AD,BC上,AN和BM交于点E,CM和DN交于点F,连接EF.
(1)当M,N分别为AD,BC的中点时,试判断四边形MENF的形状,并说明理由;
(2)试探求:
①当AM,BN满足什么条件时,一定有EFAD?并说明理由;
②当AM,BN满足什么条件时,一定有四边形MENF为平行四边形?并说明理由.
24.如图,平行四边形ADBC中,∠C=60°,AC=BC,点E、F分别在BC、AC上,BE=CF,AE=BF交于点G.
(1)求∠EGB的度数;
(2)连接DG,求证:DG=AG+BG.
25.如图,在△ABC中,AD是∠BAC的平分线,BE=EC,过点E作GH⊥AD分别交AC和AD、AB的延长线于点H、F、G.求证:AC﹣AB=2BG.
26.如图,在四边形ABCD中,AB=CD,E,F分别是BC,AD的中点,延长BA和CD分别与EF的延长线交于K,H.求证:∠BKE=∠CHE.
27.如图,△ABC中,M为BC的中点,AD为∠BAC的平分线,BD⊥AD于D.
(1)求证:DM=(AC﹣AB);
(2)若AD=6,BD=8,DM=2,求AC的长.
参考答案
1.解:连接BD,过M作MG∥AB交BD于G,连接NG.如图所示:
∵M是边AD的中点,AB=3,MG∥AB,
∴MG是△ABD的中位线,
∴BG=GD,MG=AB=,
∵N是BC的中点,BG=GD,CD=5,
∴NG是△BCD的中位线,
∴NG=CD=,
在△MNG中,由三角形三边关系可知NG﹣MG<MN<MG+NG,
即<MN<,
∴1<MN<4,
当MN=MG+NG,即MN=4时,四边形ABCD是梯形,
故线段MN长的取值范围是1<MN≤4.
故选:B.
2.解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OB=OD,
又∵OE⊥BD,
∴OE是线段BD的中垂线,
∴BE=DE,
∴AE+ED=AE+BE,
∵?ABCD的周长为16cm,
∴AB+AD=8cm,
∴△ABE的周长=AB+AD=AB+AE+BE=8cm,
故选:B.
3.解:如图,连接AC与BD相交于O,
在?ABCD中,OA=OC,OB=OD,
要使四边形AECF为平行四边形,只需证明得到OE=OF即可;
A、若BE=DF,则OB﹣BE=OD﹣DF,即OE=OF,故本选项不符合题意;
B、若AE=CF,则无法判断OE=OE,故本选项符合题意;
C、AF∥CE能够利用“角角边”证明△AOF和△COE全等,从而得到OE=OF,故本选项不符合题意;
D、由∠BAE=∠DCF,从而推出△DFC≌△BEA,然后得出∠DFC=∠BEA,∴∠CFE=∠AEF,∴FC∥AE,由全等可知FC=AE,所以四边形AECF是平行四边形;故本选项不符合题意;
故选:B.
4.解:延长CF交AB于G,如图所示:
∵AD是△ABC的角平分线,
∴∠GAF=∠CAF,
在△AGF和△ACF中,,
∴△AGF≌△ACF(ASA),
∴AG=AC=5,GF=CF,
则BG=AB﹣AG=13﹣5=8.
又∵AE是△ABC的中线,
∴BE=CE,
∴EF是△BCG的中位线,
∴EF=BG=4.
故选:D.
5.解:连接AE,并延长交CD于K,
∵AB∥CD,
∴∠BAE=∠DKE,∠ABD=∠EDK,
∵点E、F、G分别是BD、AC、DC的中点.
∴BE=DE,
在△AEB和△KED中,,
∴△AEB≌△KED(AAS),
∴DK=AB,AE=EK,EF为△ACK的中位线,
∴EF=CK=(DC﹣DK)=(DC﹣AB),
∵EG为△BCD的中位线,
∴EG=BC,
又FG为△ACD的中位线,
∴FG=AD,
∴EG+GF=(AD+BC),
∵AD+BC=12,AB=5,DC=11,即DC﹣AB=6,
∴EG+GF=6,FE=3,
∴△EFG的周长是6+3=9.
故选:B.
6.解:
∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
A、∵AC=10,BD=12,
∴OA=5,OD=6,
∵6﹣5<10<6+5,
∴此时能组成三角形,故本选项符合题意;
B、∵AC=12,BD=32,
∴OA=6,OD=16,
∵16﹣6=10,
∴此时不能组成三角形,故本选项不符合题意;
C、∵AC=6,BD=8,
∴OA=3,OD=4,
∵3+4<10,
∴此时不能组成三角形,故本选项不符合题意;
D、∵AC=8,BD=10,
∴OA=4,OD=5,
∵4+5<10,
∴此时不能组成三角形,故本选项不符合题意;
故选:A.
7.解:∵M为CD中点,
∴CM=DM=CD=AB=BC=AD,
∴∠DAM=∠DMA,∠CBM=∠CMB,
∵∠C+∠D=180°,
∴∠C=2∠DMA,∠D=2∠CMB
∴∠DMA+∠CMB=(∠C+∠D)=90°,
∴∠AMB=180°﹣(∠DMA+∠CMB)=90°,
即△MAB为直角三角形,
∵BM=1,AM=2,
∴CD=AB=,
故选:D.
8.解:如图,延长EF,GC两条线相交于点H,过点G作GP∥EF交BC于点P,
∵四边形ABCD是平行四边形,
∴BC=AD=6,
∵BF=BE=8,
∴CF=BF﹣BC=2,
∵CE平分∠BEF,
∴∠GEC=∠HEC,
∵CE⊥GC,
∴∠ECG=∠ECH=90°,
在△ECG和△ECH中,
,
∴△ECG≌△ECH(ASA),
∴CG=CH,
∵GP∥EF,
∴∠PGC=∠FHC,
在△PCG和△FCH中,
,
∴△PCG≌△FCH(ASA),
∴CP=CF=2,
∴BP=BF﹣PF=8﹣4=4,
∵BF=BE,
∴∠BEF=∠BFE,
∵GP∥EF,
∴∠BGP=∠BEF,∠BPG=∠BFE,
∴∠BGP=∠BPG,
∴BG=BP=4.
故选:C.
9.解:根据题意有AP=t,CQ=2t,PD=12﹣t,BQ=15﹣2t.
①∵AD∥BC,
∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15﹣2t,
解得t=5.
∴t=5s时四边形APQB是平行四边形;
②AP=tcm,CQ=2tcm,
∵AD=12cm,BC=15cm,
∴PD=AD﹣AP=12﹣t,
∵AD∥BC,
∴当PD=QC时,四边形PDCQ是平行四边形.
即:12﹣t=2t,
解得t=4s,
∴当t=4s时,四边形PDCQ是平行四边形.
综上所述,当P,Q同时出发4或5秒后其中一个新四边形为平行四边形.
故答案是:4或5.
10.解:如图,延长DC和FE交于点G,
在平行四边形ABCD中,AB∥CD,
∴∠B=∠ECG,
∵E为BC的中点,
∴BE=CE=BC=×4=2,
在△BEF和△CEG中,
,
∴△BEF≌△CEG(ASA),
∴BF=CG,
∵∠B=60°,
∴∠FEB=30°,
∴BF=BE=1,
∴EF=,
∵CG=BF=1,CD=AB=3,
∴DG=CD+CG=3+1=4,
∵EF⊥AB,AB∥CD,
∴DG⊥FG,
∴S△DEF=EF?DG=××4=2.
故答案为:2.
11.解:在平行四边形ABCD中,AB∥CD,
∴∠ABE=∠BEC.
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠CBE=∠BEC,
∴CB=CE.
∵CF⊥BE,
∴BF=EF.
∵G是AB的中点,
∴GF是△ABE的中位线,
∴GF=AE,
∵AE=4,
∴GF=2.
故答案为2.
12.解:∵BN平分∠ABC,BN⊥AE,
∴∠NBA=∠NBE,∠BNA=∠BNE,
在△BNA和△BNE中,
.
∴△BNA≌△BNE(ASA),
∴BA=BE,
∴△BAE是等腰三角形,
同理△CAD是等腰三角形,
∴点N是AE中点,点M是AD中点(三线合一),
∴MN是△ADE的中位线,
∵BE+CD=AB+AC=19﹣BC=19﹣7=12,
∴DE=BE+CD﹣BC=5,
∴MN=DE=.
故答案是:.
13.解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,AD∥BC,
∴∠AEB=∠CBE,
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
∵∠ABC的平分线分对边AD为2和3两部分,
如果AE=2,则四边形周长为14;
如果AE=3,则AB=AC=3,AD=BC=5,
∴?ABCD的周长为16;
∴?ABCD的周长为14或16.
故答案为:14或16.
14.解:∵DE是△ABC的中位线,
∴DE=BC=4.
∵∠AFB=90°,D是AB的中点,
∴DF=AB=2.5,
∴EF=DE﹣DF=4﹣2.5=1.5.
故答案为:1.5.
15.解:延长CM交AB于G,延长CN交AB于H,
∵∠ACB=90°,AC=6,BC=8,
∴AB=10,
在△BMC和△BMG中,
,
∴△BMC≌△BMG,
∴BG=BC=8,CM=MG,
∴AG=2,
同理,AH=AC=6,CN=NH,
∴GH=4,
∴MN=GH=2,
故答案为:2.
16.解:∵两组对边分别平行的四边形是平行四边形,∴可以分以下三种情况分别求出D点的坐标:
①当AB∥CD,AC∥BD时,D点的坐标为(9,0);
②当AD∥BC,AC∥BD时,D点的坐标为(﹣1,6);
③当AB∥CD,AD∥BC时,D点的坐标为(3,﹣4).
故D点坐标为(9,0)或(﹣1,6)或(3,﹣4);
故答案为:(9,0)或(﹣1,6)或(3,﹣4).
17.解:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=CD,
∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE=CD,
即D为CE中点,
∵EF⊥BC,
∴∠EFC=90°,
∵AB∥CD,
∴∠DCF=∠ABC=60°,
∴∠CEF=30°,
∴CE=2CF=2,
∴AB=1;
故答案为:1.
18.解:过E作EM∥AB与GC交于点M,
∴△EMF≌△DGF,
∴EM=GD,
∵DE是中位线,
∴CE=AC,
又∵EM∥AG,
∴△CME∽△CGA,
∴EM:AG=CE:AC=1:2,
又∵EM=GD,
∴AG:GD=2:1.
∵AB=6,
∴AD=3,
∴AG=,
故答案为:2
19.解:延长BD交AC于H,
在△ADB和△ADH中,
,
∴△ADB≌△ADH,
∴AH=AB=7,BD=DH,
∴HC=AC﹣AH=4,
∵BD=DH,BE=EC,
∴DE=CH=2,
故答案为:2.
20.解:①当点F在线段BM上,AE=FM时,以A、M、E、F为顶点的四边形是平行四边形,
则有t=9+3t﹣12,解得t=,
②当F在线段CM上,AE=FM时,以A、M、E、F为顶点的四边形是平行四边形,
则有t=12﹣9﹣3t,解得t=,
综上所述,t=或s时,以A、M、E、F为顶点的四边形是平行四边形.
故答案为:或
21.(1)证明:∵在平行四边形ABCD中,AD∥BC,BC=AD,
∴∠EAD=∠AEB,
又∵AB=AE,
∴∠B=∠AEB,
∴∠B=∠EAD,
在△ABC和△EAD中,
,
∴△ABC≌△EAD(SAS).
(2)解:∵AB=AE,
∴∠B=∠AEB,
∴∠BAE=50°,
∴∠BAC=∠BAE+∠EAC=50°+25°=75°,
∵△ABC≌△EAD,
∴∠AED=∠BAC=75°.
22.证明:(1)①∠ACB=∠GCD.
理由:∵AB=AC,
∴∠ABC=∠ACB,
∵CG∥AB,
∴∠ABC=∠GCD,
∴∠ACB=∠GCD;
②∵四边形CDFE是平行四边形,
∴∠CEG=∠ACB,∠CGE=∠GCD,
∴∠CEG=∠CGE,
∴CE=CG,
∵∠ACB+∠ECG=∠ECG+∠GCD,
即∠BCG=∠ECD,
在△BCG和△DCE中,
∵,
∴△BCG≌△DCE(SAS);
(2)①∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABE是等边三角形,EF⊥AB,
∴∠AEF=30°
∴AE=2AF,且AB=2AF,
∴AF=CB,
而∠ACB=∠AFE=90°,
在Rt△AFE和Rt△BCA中,
∵,
∴△AFE≌△BCA(HL),
∴AC=EF;
②由①知道AC=EF,
而△ACD是等边三角形,
∴∠DAC=60°
∴EF=AC=AD,且AD⊥AB,
而EF⊥AB,
∴EF∥AD,
∴四边形ADFE是平行四边形.
23.(1)解:四边形MENF是平行四边形.
理由如下:在平行四边形ABCD中,AD=BC,
∵M,N分别为AD,BC的中点,
∴AM=AD,CN=BC,
∴AM=CN,
又∵AD∥BC,
∴四边形ANCM是平行四边形,
∴AN∥CM,
同理可得BM∥DN,
∴四边形MENF是平行四边形;
(2)解:①当AM=BN时,一定有EFAD.
理由如下:∵AM=BN,
∴DM=NC,
在△AEM和△NEB中
∵,
∴△AEM≌△NEB(ASA),
∴ME=BE,
同理可得出:DF=NF,
∴EF是△AND的中位线,
∴EFAD;
②当AM+BN=AD时,四边形MENF为平行四边形.
理由如下:在平行四边形ABCD中,AD=BC,
∵AM+BN=AD,BN+CN=BC,
∴AM=CN,
又∵AD∥BC,
∴四边形ANCM是平行四边形,
∴AN∥CM,
同理可得BM∥DN,
∴四边形MENF是平行四边形.
24.(1)解:∠C=60°,AC=BC,
∴△ABC是等边三角形,
∴∠ABC=∠C=60°,
∵在△ABE和△BCF中,
,
∴△ABE≌△BCF(SAS),
∴∠BAE=∠FBC,
∴∠BGE=∠ABG+∠BAE=∠ABG+∠FBC=∠ABC=60°;
(2)证明:延长GE至点H,使GH=GB,如图,
∵∠BGE=60°,
∴△BGH为等边三角形,
∴BG=BH=GH,∠GBH=60°,
∵四边形ADBC是平行四边形,
∴△ABD是等边三角形,
∴AB=BD,∠ABD=60°,
∵∠ABH=∠GBH+∠ABG,∠DBG=∠ABD+∠ABG,
∴∠ABH=∠DBG,
∵在△DBG和△ABH中,
,
∴△DBG≌△ABH(SAS),
∴DG=AH,
而AH=AG+GH,
∴DG=AG+BG.
25.证明:作EM∥AG,BN∥AC,
∵AD是∠BAC的角平分线,
∴∠GAF=∠CAF,
∵GH⊥AD,
∴∠AFG=∠AFH,
在△AGF与△AHF中,
,
∴△AGF≌△AHF(ASA),
∴AG=AH,∠G=∠AHF,
∵EM∥AG,BE=EC,
∴AM=MC,∠G=∠MEH,
∴∠MEH=∠AHF,
∴EM=HM,
∵EM是△ABC的中位线,
∴EM=AB,
∴HM=AB,
∵MC﹣MH=HC,
∴AC﹣AB=HC,
∴AC﹣AB=2HC,
∵BN∥AC,
∴∠NBE=∠ECH,∠BNG=∠AHG,
在△BEN与△CEH中,
,
∴△BEN≌△CEH(AAS),
∴BN=CH,
∵∠BNG=∠AHG,
∴∠G=∠BNG,
∴BG=BN,
∴BG=CH,
∴AC﹣AB=2BG.
26.证明:连接BD,取BD的中点I,连接IE,IF,
∵E,F分别是BC,AD的中点,
∴IE,IF分别是△ABD,△BDC的中位线,
∴IE∥CD,IE=CD,IF∥AB,IF=AB,
∵AB=CD,
∴IE=IF,
∵IE∥CD,IF∥AB,
∴∠IFE=∠BKE,∠IEF=∠CHE,
∵IF=IE,
∴∠IFE=∠IEF,
∴∠BKE=∠CHE.
27.解:(1)证明:延长BD交AC于E,
∵AD⊥BD,
∴∠ADB=∠ADE=90°,
∵AD为∠BAC的平分线,
∴∠BAD=∠EAD,
在△BAD和△EAD中,
,
∴△BAD≌△EAD(SAS),
∴AB=AE,BD=DE,
∵M为BC的中点,
∴DM=CE=(AC﹣AB);
(2)∵在Rt△ADB中,∠ADB=90°,AD=6,BD=8,
∴由勾股定理得:AE=AB==10,
∵DM=2,DM=CE,
∴CE=4,
∴AC=10+4=14.
1.已知在四边形ABCD中,AB=3,CD=5,M,N分别是AD,BC的中点,则线段MN的取值范围是( )
A.1<MN<4 B.1<MN≤4 C.2<MN<8 D.2<MN≤8
2.如图,?ABCD的周长为16cm,AB≠AD,AC和BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长是( )
A.10cm B.8m C.6m D.4cm
3.如图,在平行四边形ABCD中,E,F是对角线BD上不同的两点,连接AE,CE,AF,CF.下列条件中,不能得出四边形AECF一定是平行四边形的为( )
A.BE=DF B.AE=CF C.AF∥CE D.∠BAE=∠DCF
4.如图,在△ABC中,AD是角平分线,AE是中线,CF⊥AD于点F,AC=5,AB=13,则EF的长为( )
A. B. C.3 D.4
5.如图,四边形ABCD中,AB∥CD,AB=5,DC=11,AD与BC的和是12,点E、F、G分别是BD、AC、DC的中点,则△EFG的周长是( )
A.8 B.9 C.10 D.12
6.平行四边形ABCD的一边长为10,则它的两条对角线长可以是( )
A.10和12 B.12和32 C.6和8 D.8和10
7.如图所示,在平行四边形ABCD中,M是CD的中点,AB=2BC,BM=1,AM=2,则CD的长为( )
A. B.2 C. D.
8.如图,在平行四边形ABCD中,AD=6,点E在边AD上,点F在BC的延长线上,且满足BF=BE=8,过点C作CE的垂线交BE于点G,若CE恰好平分∠BEF,则BG的长为( )
A.2 B.3 C.4 D.2
9.如图,四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截原四边形为两个新四边形.则当P,Q同时出发 秒后其中一个新四边形为平行四边形.
10.如图所示,在平行四边形ABCD中,AB=3,BC=4,∠B=60°,E是BC的中点,EF⊥AB于点F,则△DEF的面积为 平方单位.
11.如图,在平行四边形ABCD中,BE平分∠ABC,CF⊥BE,连接AE,G是AB的中点,连接GF,若AE=4,则GF= .
12.如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为 .
13.平行四边形ABCD中,∠ABC的平分线将AD边分成的两部分的长分别为2和3,则平行四边形ABCD的周长是
.
14.如图,点D、E分别为△ABC的边AB、AC的中点,同时,点F在DE上,且∠AFB=90°,已知AB=5,BC=8,那么EF的长为 .
15.在Rt△ABC中,∠ACB=90°,AE,BD是角平分线,CM⊥BD于M,CN⊥AE于N,若AC=6,BC=8,则MN= .
16.已知A(1,1),B(4,3),C(6,﹣2),在平面直角坐标找一点D,使以A、B、C、D四点的四边形为平行四边形,则D点的坐标是 .
17.如图,平行四边形ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,CF=1,则AB的长是 .
18.如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于G,AB=6,则AG= .
19.如图,△ABC中,AB=7,AC=11,AD平分∠BAC,BD⊥AD,E是BC的中点,那么DE=
20.如图,四边形ABCD中,AD∥BC,AD=8cm,BC=12cm,M是BC上一点,且BM=9cm,点E从点A出发以1cm/s的速度向点D运动,点F从点C出发,以3cm/s的速度向点B运动,当其中一点到达终点,另一点也随之停止,设运动时间为t,则当以A、M、E、F为顶点的四边形是平行四边形时,t=
21.如图,在?ABCD中,E为BC边上一点,且AB=AE.
(1)求证:△ABC≌△EAD;
(2)若∠B=65°,∠EAC=25°,求∠AED的度数.
22.证明:(1)如图1,△ABC中,AB=AC,延长BC至D,使CD=BC,点E在边AC上,以CE、CD为邻边作?CDFE,过点C作CG∥AB交EF于点G.连接BG、DE.
①∠ACB与∠GCD有怎样的数量关系?请说明理由.
②求证:△BCG≌△DCE.
(2)如图2,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
①试说明AC=EF;
②求证:四边形ADFE是平行四边形.
23.如图所示,在平行四边形ABCD中,M,N分别在AD,BC上,AN和BM交于点E,CM和DN交于点F,连接EF.
(1)当M,N分别为AD,BC的中点时,试判断四边形MENF的形状,并说明理由;
(2)试探求:
①当AM,BN满足什么条件时,一定有EFAD?并说明理由;
②当AM,BN满足什么条件时,一定有四边形MENF为平行四边形?并说明理由.
24.如图,平行四边形ADBC中,∠C=60°,AC=BC,点E、F分别在BC、AC上,BE=CF,AE=BF交于点G.
(1)求∠EGB的度数;
(2)连接DG,求证:DG=AG+BG.
25.如图,在△ABC中,AD是∠BAC的平分线,BE=EC,过点E作GH⊥AD分别交AC和AD、AB的延长线于点H、F、G.求证:AC﹣AB=2BG.
26.如图,在四边形ABCD中,AB=CD,E,F分别是BC,AD的中点,延长BA和CD分别与EF的延长线交于K,H.求证:∠BKE=∠CHE.
27.如图,△ABC中,M为BC的中点,AD为∠BAC的平分线,BD⊥AD于D.
(1)求证:DM=(AC﹣AB);
(2)若AD=6,BD=8,DM=2,求AC的长.
参考答案
1.解:连接BD,过M作MG∥AB交BD于G,连接NG.如图所示:
∵M是边AD的中点,AB=3,MG∥AB,
∴MG是△ABD的中位线,
∴BG=GD,MG=AB=,
∵N是BC的中点,BG=GD,CD=5,
∴NG是△BCD的中位线,
∴NG=CD=,
在△MNG中,由三角形三边关系可知NG﹣MG<MN<MG+NG,
即<MN<,
∴1<MN<4,
当MN=MG+NG,即MN=4时,四边形ABCD是梯形,
故线段MN长的取值范围是1<MN≤4.
故选:B.
2.解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OB=OD,
又∵OE⊥BD,
∴OE是线段BD的中垂线,
∴BE=DE,
∴AE+ED=AE+BE,
∵?ABCD的周长为16cm,
∴AB+AD=8cm,
∴△ABE的周长=AB+AD=AB+AE+BE=8cm,
故选:B.
3.解:如图,连接AC与BD相交于O,
在?ABCD中,OA=OC,OB=OD,
要使四边形AECF为平行四边形,只需证明得到OE=OF即可;
A、若BE=DF,则OB﹣BE=OD﹣DF,即OE=OF,故本选项不符合题意;
B、若AE=CF,则无法判断OE=OE,故本选项符合题意;
C、AF∥CE能够利用“角角边”证明△AOF和△COE全等,从而得到OE=OF,故本选项不符合题意;
D、由∠BAE=∠DCF,从而推出△DFC≌△BEA,然后得出∠DFC=∠BEA,∴∠CFE=∠AEF,∴FC∥AE,由全等可知FC=AE,所以四边形AECF是平行四边形;故本选项不符合题意;
故选:B.
4.解:延长CF交AB于G,如图所示:
∵AD是△ABC的角平分线,
∴∠GAF=∠CAF,
在△AGF和△ACF中,,
∴△AGF≌△ACF(ASA),
∴AG=AC=5,GF=CF,
则BG=AB﹣AG=13﹣5=8.
又∵AE是△ABC的中线,
∴BE=CE,
∴EF是△BCG的中位线,
∴EF=BG=4.
故选:D.
5.解:连接AE,并延长交CD于K,
∵AB∥CD,
∴∠BAE=∠DKE,∠ABD=∠EDK,
∵点E、F、G分别是BD、AC、DC的中点.
∴BE=DE,
在△AEB和△KED中,,
∴△AEB≌△KED(AAS),
∴DK=AB,AE=EK,EF为△ACK的中位线,
∴EF=CK=(DC﹣DK)=(DC﹣AB),
∵EG为△BCD的中位线,
∴EG=BC,
又FG为△ACD的中位线,
∴FG=AD,
∴EG+GF=(AD+BC),
∵AD+BC=12,AB=5,DC=11,即DC﹣AB=6,
∴EG+GF=6,FE=3,
∴△EFG的周长是6+3=9.
故选:B.
6.解:
∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
A、∵AC=10,BD=12,
∴OA=5,OD=6,
∵6﹣5<10<6+5,
∴此时能组成三角形,故本选项符合题意;
B、∵AC=12,BD=32,
∴OA=6,OD=16,
∵16﹣6=10,
∴此时不能组成三角形,故本选项不符合题意;
C、∵AC=6,BD=8,
∴OA=3,OD=4,
∵3+4<10,
∴此时不能组成三角形,故本选项不符合题意;
D、∵AC=8,BD=10,
∴OA=4,OD=5,
∵4+5<10,
∴此时不能组成三角形,故本选项不符合题意;
故选:A.
7.解:∵M为CD中点,
∴CM=DM=CD=AB=BC=AD,
∴∠DAM=∠DMA,∠CBM=∠CMB,
∵∠C+∠D=180°,
∴∠C=2∠DMA,∠D=2∠CMB
∴∠DMA+∠CMB=(∠C+∠D)=90°,
∴∠AMB=180°﹣(∠DMA+∠CMB)=90°,
即△MAB为直角三角形,
∵BM=1,AM=2,
∴CD=AB=,
故选:D.
8.解:如图,延长EF,GC两条线相交于点H,过点G作GP∥EF交BC于点P,
∵四边形ABCD是平行四边形,
∴BC=AD=6,
∵BF=BE=8,
∴CF=BF﹣BC=2,
∵CE平分∠BEF,
∴∠GEC=∠HEC,
∵CE⊥GC,
∴∠ECG=∠ECH=90°,
在△ECG和△ECH中,
,
∴△ECG≌△ECH(ASA),
∴CG=CH,
∵GP∥EF,
∴∠PGC=∠FHC,
在△PCG和△FCH中,
,
∴△PCG≌△FCH(ASA),
∴CP=CF=2,
∴BP=BF﹣PF=8﹣4=4,
∵BF=BE,
∴∠BEF=∠BFE,
∵GP∥EF,
∴∠BGP=∠BEF,∠BPG=∠BFE,
∴∠BGP=∠BPG,
∴BG=BP=4.
故选:C.
9.解:根据题意有AP=t,CQ=2t,PD=12﹣t,BQ=15﹣2t.
①∵AD∥BC,
∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15﹣2t,
解得t=5.
∴t=5s时四边形APQB是平行四边形;
②AP=tcm,CQ=2tcm,
∵AD=12cm,BC=15cm,
∴PD=AD﹣AP=12﹣t,
∵AD∥BC,
∴当PD=QC时,四边形PDCQ是平行四边形.
即:12﹣t=2t,
解得t=4s,
∴当t=4s时,四边形PDCQ是平行四边形.
综上所述,当P,Q同时出发4或5秒后其中一个新四边形为平行四边形.
故答案是:4或5.
10.解:如图,延长DC和FE交于点G,
在平行四边形ABCD中,AB∥CD,
∴∠B=∠ECG,
∵E为BC的中点,
∴BE=CE=BC=×4=2,
在△BEF和△CEG中,
,
∴△BEF≌△CEG(ASA),
∴BF=CG,
∵∠B=60°,
∴∠FEB=30°,
∴BF=BE=1,
∴EF=,
∵CG=BF=1,CD=AB=3,
∴DG=CD+CG=3+1=4,
∵EF⊥AB,AB∥CD,
∴DG⊥FG,
∴S△DEF=EF?DG=××4=2.
故答案为:2.
11.解:在平行四边形ABCD中,AB∥CD,
∴∠ABE=∠BEC.
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠CBE=∠BEC,
∴CB=CE.
∵CF⊥BE,
∴BF=EF.
∵G是AB的中点,
∴GF是△ABE的中位线,
∴GF=AE,
∵AE=4,
∴GF=2.
故答案为2.
12.解:∵BN平分∠ABC,BN⊥AE,
∴∠NBA=∠NBE,∠BNA=∠BNE,
在△BNA和△BNE中,
.
∴△BNA≌△BNE(ASA),
∴BA=BE,
∴△BAE是等腰三角形,
同理△CAD是等腰三角形,
∴点N是AE中点,点M是AD中点(三线合一),
∴MN是△ADE的中位线,
∵BE+CD=AB+AC=19﹣BC=19﹣7=12,
∴DE=BE+CD﹣BC=5,
∴MN=DE=.
故答案是:.
13.解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,AD∥BC,
∴∠AEB=∠CBE,
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
∵∠ABC的平分线分对边AD为2和3两部分,
如果AE=2,则四边形周长为14;
如果AE=3,则AB=AC=3,AD=BC=5,
∴?ABCD的周长为16;
∴?ABCD的周长为14或16.
故答案为:14或16.
14.解:∵DE是△ABC的中位线,
∴DE=BC=4.
∵∠AFB=90°,D是AB的中点,
∴DF=AB=2.5,
∴EF=DE﹣DF=4﹣2.5=1.5.
故答案为:1.5.
15.解:延长CM交AB于G,延长CN交AB于H,
∵∠ACB=90°,AC=6,BC=8,
∴AB=10,
在△BMC和△BMG中,
,
∴△BMC≌△BMG,
∴BG=BC=8,CM=MG,
∴AG=2,
同理,AH=AC=6,CN=NH,
∴GH=4,
∴MN=GH=2,
故答案为:2.
16.解:∵两组对边分别平行的四边形是平行四边形,∴可以分以下三种情况分别求出D点的坐标:
①当AB∥CD,AC∥BD时,D点的坐标为(9,0);
②当AD∥BC,AC∥BD时,D点的坐标为(﹣1,6);
③当AB∥CD,AD∥BC时,D点的坐标为(3,﹣4).
故D点坐标为(9,0)或(﹣1,6)或(3,﹣4);
故答案为:(9,0)或(﹣1,6)或(3,﹣4).
17.解:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=CD,
∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE=CD,
即D为CE中点,
∵EF⊥BC,
∴∠EFC=90°,
∵AB∥CD,
∴∠DCF=∠ABC=60°,
∴∠CEF=30°,
∴CE=2CF=2,
∴AB=1;
故答案为:1.
18.解:过E作EM∥AB与GC交于点M,
∴△EMF≌△DGF,
∴EM=GD,
∵DE是中位线,
∴CE=AC,
又∵EM∥AG,
∴△CME∽△CGA,
∴EM:AG=CE:AC=1:2,
又∵EM=GD,
∴AG:GD=2:1.
∵AB=6,
∴AD=3,
∴AG=,
故答案为:2
19.解:延长BD交AC于H,
在△ADB和△ADH中,
,
∴△ADB≌△ADH,
∴AH=AB=7,BD=DH,
∴HC=AC﹣AH=4,
∵BD=DH,BE=EC,
∴DE=CH=2,
故答案为:2.
20.解:①当点F在线段BM上,AE=FM时,以A、M、E、F为顶点的四边形是平行四边形,
则有t=9+3t﹣12,解得t=,
②当F在线段CM上,AE=FM时,以A、M、E、F为顶点的四边形是平行四边形,
则有t=12﹣9﹣3t,解得t=,
综上所述,t=或s时,以A、M、E、F为顶点的四边形是平行四边形.
故答案为:或
21.(1)证明:∵在平行四边形ABCD中,AD∥BC,BC=AD,
∴∠EAD=∠AEB,
又∵AB=AE,
∴∠B=∠AEB,
∴∠B=∠EAD,
在△ABC和△EAD中,
,
∴△ABC≌△EAD(SAS).
(2)解:∵AB=AE,
∴∠B=∠AEB,
∴∠BAE=50°,
∴∠BAC=∠BAE+∠EAC=50°+25°=75°,
∵△ABC≌△EAD,
∴∠AED=∠BAC=75°.
22.证明:(1)①∠ACB=∠GCD.
理由:∵AB=AC,
∴∠ABC=∠ACB,
∵CG∥AB,
∴∠ABC=∠GCD,
∴∠ACB=∠GCD;
②∵四边形CDFE是平行四边形,
∴∠CEG=∠ACB,∠CGE=∠GCD,
∴∠CEG=∠CGE,
∴CE=CG,
∵∠ACB+∠ECG=∠ECG+∠GCD,
即∠BCG=∠ECD,
在△BCG和△DCE中,
∵,
∴△BCG≌△DCE(SAS);
(2)①∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABE是等边三角形,EF⊥AB,
∴∠AEF=30°
∴AE=2AF,且AB=2AF,
∴AF=CB,
而∠ACB=∠AFE=90°,
在Rt△AFE和Rt△BCA中,
∵,
∴△AFE≌△BCA(HL),
∴AC=EF;
②由①知道AC=EF,
而△ACD是等边三角形,
∴∠DAC=60°
∴EF=AC=AD,且AD⊥AB,
而EF⊥AB,
∴EF∥AD,
∴四边形ADFE是平行四边形.
23.(1)解:四边形MENF是平行四边形.
理由如下:在平行四边形ABCD中,AD=BC,
∵M,N分别为AD,BC的中点,
∴AM=AD,CN=BC,
∴AM=CN,
又∵AD∥BC,
∴四边形ANCM是平行四边形,
∴AN∥CM,
同理可得BM∥DN,
∴四边形MENF是平行四边形;
(2)解:①当AM=BN时,一定有EFAD.
理由如下:∵AM=BN,
∴DM=NC,
在△AEM和△NEB中
∵,
∴△AEM≌△NEB(ASA),
∴ME=BE,
同理可得出:DF=NF,
∴EF是△AND的中位线,
∴EFAD;
②当AM+BN=AD时,四边形MENF为平行四边形.
理由如下:在平行四边形ABCD中,AD=BC,
∵AM+BN=AD,BN+CN=BC,
∴AM=CN,
又∵AD∥BC,
∴四边形ANCM是平行四边形,
∴AN∥CM,
同理可得BM∥DN,
∴四边形MENF是平行四边形.
24.(1)解:∠C=60°,AC=BC,
∴△ABC是等边三角形,
∴∠ABC=∠C=60°,
∵在△ABE和△BCF中,
,
∴△ABE≌△BCF(SAS),
∴∠BAE=∠FBC,
∴∠BGE=∠ABG+∠BAE=∠ABG+∠FBC=∠ABC=60°;
(2)证明:延长GE至点H,使GH=GB,如图,
∵∠BGE=60°,
∴△BGH为等边三角形,
∴BG=BH=GH,∠GBH=60°,
∵四边形ADBC是平行四边形,
∴△ABD是等边三角形,
∴AB=BD,∠ABD=60°,
∵∠ABH=∠GBH+∠ABG,∠DBG=∠ABD+∠ABG,
∴∠ABH=∠DBG,
∵在△DBG和△ABH中,
,
∴△DBG≌△ABH(SAS),
∴DG=AH,
而AH=AG+GH,
∴DG=AG+BG.
25.证明:作EM∥AG,BN∥AC,
∵AD是∠BAC的角平分线,
∴∠GAF=∠CAF,
∵GH⊥AD,
∴∠AFG=∠AFH,
在△AGF与△AHF中,
,
∴△AGF≌△AHF(ASA),
∴AG=AH,∠G=∠AHF,
∵EM∥AG,BE=EC,
∴AM=MC,∠G=∠MEH,
∴∠MEH=∠AHF,
∴EM=HM,
∵EM是△ABC的中位线,
∴EM=AB,
∴HM=AB,
∵MC﹣MH=HC,
∴AC﹣AB=HC,
∴AC﹣AB=2HC,
∵BN∥AC,
∴∠NBE=∠ECH,∠BNG=∠AHG,
在△BEN与△CEH中,
,
∴△BEN≌△CEH(AAS),
∴BN=CH,
∵∠BNG=∠AHG,
∴∠G=∠BNG,
∴BG=BN,
∴BG=CH,
∴AC﹣AB=2BG.
26.证明:连接BD,取BD的中点I,连接IE,IF,
∵E,F分别是BC,AD的中点,
∴IE,IF分别是△ABD,△BDC的中位线,
∴IE∥CD,IE=CD,IF∥AB,IF=AB,
∵AB=CD,
∴IE=IF,
∵IE∥CD,IF∥AB,
∴∠IFE=∠BKE,∠IEF=∠CHE,
∵IF=IE,
∴∠IFE=∠IEF,
∴∠BKE=∠CHE.
27.解:(1)证明:延长BD交AC于E,
∵AD⊥BD,
∴∠ADB=∠ADE=90°,
∵AD为∠BAC的平分线,
∴∠BAD=∠EAD,
在△BAD和△EAD中,
,
∴△BAD≌△EAD(SAS),
∴AB=AE,BD=DE,
∵M为BC的中点,
∴DM=CE=(AC﹣AB);
(2)∵在Rt△ADB中,∠ADB=90°,AD=6,BD=8,
∴由勾股定理得:AE=AB==10,
∵DM=2,DM=CE,
∴CE=4,
∴AC=10+4=14.
