第二章 相交线与平行线 单元测试 卷(Word版含解析)
文档属性
| 名称 | 第二章 相交线与平行线 单元测试 卷(Word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 198.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 00:00:00 | ||
图片预览


文档简介
第二章 相交线与平行线 单元测试卷
一.选择题
1.在同一平面内,过直线上一点作已知直线的垂线,能作( )
A.1条 B.2条 C.3条 D.无数条
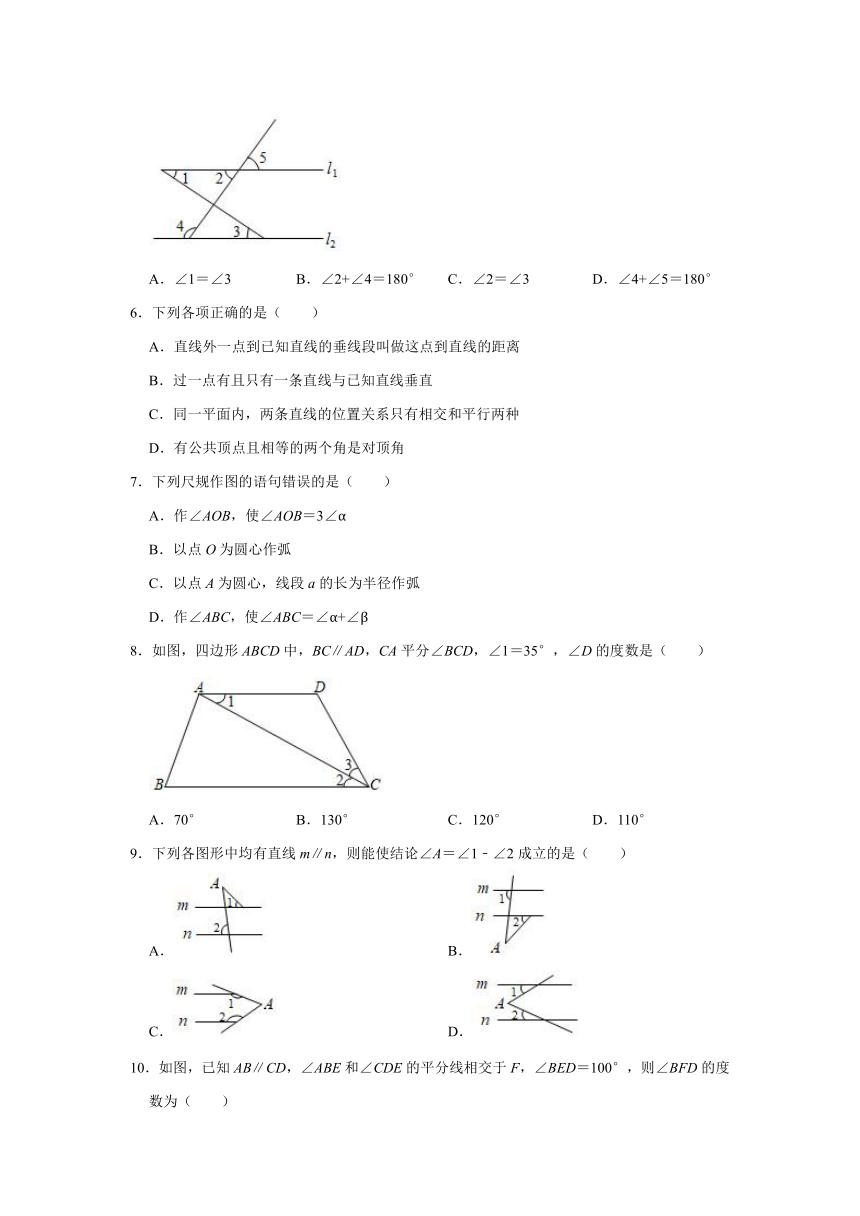
2.如图,小明画了两条直线AB,CD相交于点O,则∠1和∠2是( )
A.对顶角 B.同位角 C.内错角 D.邻补角
3.如图,点E、F分别是AB、CD上的点,点G是BC的延长线上一点,且∠B=∠DCG=∠D,则下列判断不一定成立的是( )
A.AB∥CD B.AD∥BG
C.∠B=∠AEF D.∠BEF+∠EFC=180°
4.如图图形中,∠1和∠2不是同位角的是( )
A. B.
C. D.
5.如图,下列条件中,不能判定l1∥l2的是( )
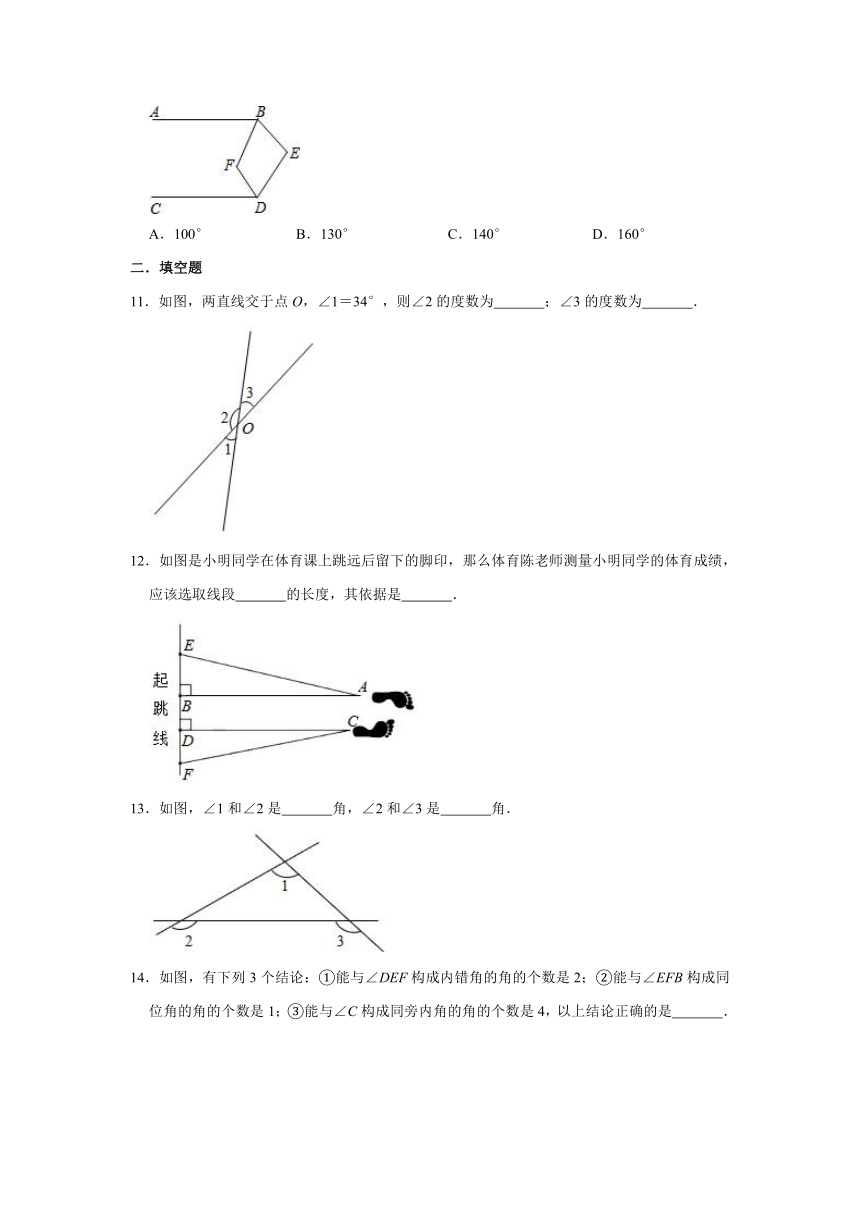
A.∠1=∠3 B.∠2+∠4=180° C.∠2=∠3 D.∠4+∠5=180°
6.下列各项正确的是( )
A.直线外一点到已知直线的垂线段叫做这点到直线的距离
B.过一点有且只有一条直线与已知直线垂直
C.同一平面内,两条直线的位置关系只有相交和平行两种
D.有公共顶点且相等的两个角是对顶角
7.下列尺规作图的语句错误的是( )
A.作∠AOB,使∠AOB=3∠α
B.以点O为圆心作弧
C.以点A为圆心,线段a的长为半径作弧
D.作∠ABC,使∠ABC=∠α+∠β
8.如图,四边形ABCD中,BC∥AD,CA平分∠BCD,∠1=35°,∠D的度数是( )
A.70° B.130° C.120° D.110°
9.下列各图形中均有直线m∥n,则能使结论∠A=∠1﹣∠2成立的是( )
A. B.
C. D.
10.如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠BED=100°,则∠BFD的度数为( )
A.100° B.130° C.140° D.160°
二.填空题
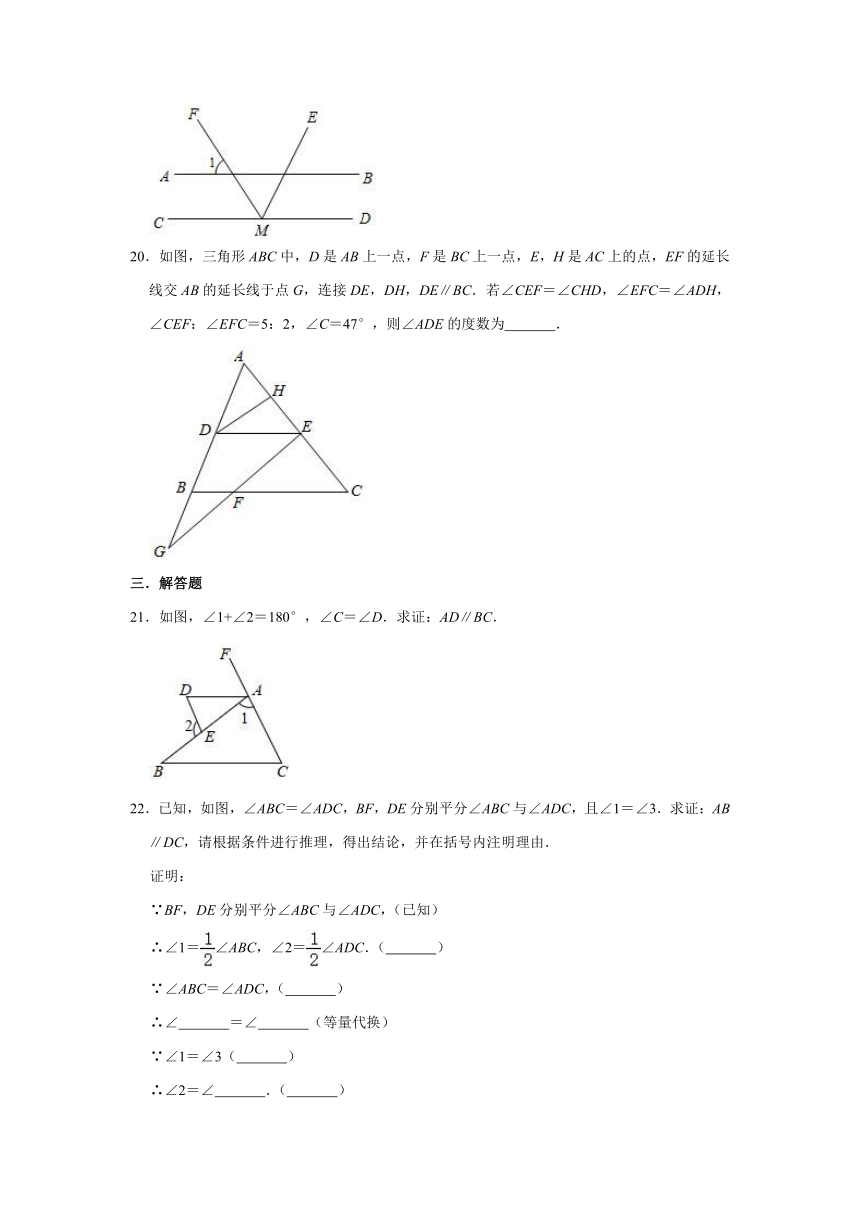
11.如图,两直线交于点O,∠1=34°,则∠2的度数为 ;∠3的度数为 .
12.如图是小明同学在体育课上跳远后留下的脚印,那么体育陈老师测量小明同学的体育成绩,应该选取线段 的长度,其依据是 .
13.如图,∠1和∠2是 角,∠2和∠3是 角.
14.如图,有下列3个结论:①能与∠DEF构成内错角的角的个数是2;②能与∠EFB构成同位角的角的个数是1;③能与∠C构成同旁内角的角的个数是4,以上结论正确的是 .
15.如图,∠A=70°,O是AB上一点,直线OD与AB所夹的∠BOD=78°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转 .
16.将一块三角板ABC(∠BAC=90°,∠ABC=30°)按如图方式放置,使A,B两点分别落在直线m,n上.对于给出的四个条件:①∠1=25.5°,∠2=55°30';②∠2=2∠1;③∠1+∠2=90°;④∠ACB=∠1+∠2;⑤∠ABC=∠2﹣∠1.能判断直线m∥n的有 .(填序号)
17.将一副三角板(∠A=30°)按如图所示方式摆放,使得AB∥EF,则∠1等于 度.
18.如图,已知AB∥CE,∠B=50°,CE平分∠ACD,则∠ACD= °
19.如图,AB∥CD,点M为CD上一点,MF平分∠CME.若∠1=57°,则∠EMD的大小为 度.
20.如图,三角形ABC中,D是AB上一点,F是BC上一点,E,H是AC上的点,EF的延长线交AB的延长线于点G,连接DE,DH,DE∥BC.若∠CEF=∠CHD,∠EFC=∠ADH,∠CEF:∠EFC=5:2,∠C=47°,则∠ADE的度数为 .
三.解答题
21.如图,∠1+∠2=180°,∠C=∠D.求证:AD∥BC.
22.已知,如图,∠ABC=∠ADC,BF,DE分别平分∠ABC与∠ADC,且∠1=∠3.求证:AB∥DC,请根据条件进行推理,得出结论,并在括号内注明理由.
证明:
∵BF,DE分别平分∠ABC与∠ADC,(已知)
∴∠1=∠ABC,∠2=∠ADC.( )
∵∠ABC=∠ADC,( )
∴∠ =∠ (等量代换)
∵∠1=∠3( )
∴∠2=∠ .( )
∴ ∥ .( )
23.如图,AB∥CD,∠FGB=154°,FG平分∠EFD,求∠AEF的度数.
24.如图,将一张上、下两边平行(即AB∥CD)的纸带沿直线MN折叠,EF为折痕.
(1)试说明∠1=∠2;
(2)已知∠2=40°,求∠BEF的度数.
25.已知:如图,AB∥DE,CM平分∠BCE,CN⊥CM.求证:∠B=2∠DCN.
26.如图,直线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值.
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
参考答案
一.选择题
1.解:在同一平面内,过直线上一点作已知直线的垂线,能作1条.
故选:A.
2.解:由对顶角的定义可知,∠1和∠2是对顶角,
故选:A.
3.解:A、∵∠B=∠DCG=∠D,
∴AB∥DC,AD∥BG,正确,故本选项不符合题意;
B、∵∠B=∠DCG=∠D,
∴AB∥DC,AD∥BG,正确,故本选项不符合题意;
C、根据AB∥DC,AD∥BG不能推出EF∥BC,所以不能推出∠B=∠AEF,错误,故本选项符合题意;
D、∵AB∥CD,
∴∠BEF+∠EFC=180°,正确,故本选项不符合题意;
故选:C.
4.解:∵选项B中∠1和∠2是由四条直线组成,
∴∠1和∠2不是同位角.
故选:B.
5.解:A、∵∠1=∠3,
∴直线l1∥l2,故此选项不合题意;
B、∵∠2+∠4=180°,
∴直线l1∥l2,故此选项不合题意;
C、∠2=∠3,不能得出直线l1∥l2,故此选项符合题意;
D、∵∠2=∠5,4+∠5=180°,
∴4+∠2=180°,
∴直线l1∥l2,故此选项不合题意.
故选:C.
6.解:A、从直线外一点到这条直线的垂线段的长度叫做点到直线的距离,故此选项错误,不合题意;
B、在同一平面内,经过一点能画一条且只能画一条直线与已知直线垂直,故此选项错误,不合题意;
C、同一平面内,两条直线的位置关系只有相交和平行两种,正确,符合题意;
D、有公共顶点且相等的两个角不一定是对顶角,故此选项错误,不合题意.
故选:C.
7.解:A、作一个角等于已知角的倍数是常见的尺规作图,正确;
B、画弧既需要圆心,还需要半径,缺少半径长,错误.
C、以点A为圆心,线段a的长为半径作弧,正确;
D、作∠ABC,使∠ABC=∠α+∠β,正确
故选:B.
8.解:∵BC∥AD,
∴∠1=∠2=35°,
又∵CA平分∠BCD,
∴∠2=∠3=35°,
则∠BCD=70°,
∴∠D=180°﹣∠BCD=180°﹣70°=110°.
故选:D.
9.解:A、∵m∥n,
∴∠2=∠1+∠A,
∴∠A=∠2﹣∠1,不符合题意;
B、∵m∥n,
∴∠1=∠2+∠A,
∴∠A=∠1﹣∠2,符合题意;
C、∵m∥n,
∴∠1+∠2+∠A=360°,
∴∠A=360°﹣∠2﹣∠1,不符合题意;
D、∵m∥n,
∴∠A=∠1+∠2,不符合题意;
故选:B.
10.解:连接BD,
∵AB∥CD,
∴∠ABD+∠CDB=180°,
∴∠ABE+∠E+∠CDE=180°+180°=360°,
∴∠ABE+∠CDE=360°﹣100°=260°,
又∵BF、DF平分∠ABE和∠CDE,
∴∠FBE+∠FDE=130°,
∴∠BFD=360°﹣100°﹣130°=130°.
故选:B.
二.填空题
11.解:∵∠1=34°,∠1+∠2=180°,
∴∠2=180°﹣∠1=180°﹣34°=146°,
∵∠1与∠3是对顶角,∠1=34°,
∴∠3=∠1=34°.
故答案为:146°,34°.
12.解:小明同学的体育成绩,应该选取线段CD的长度.依据为:垂线段最短.
故答案为:CD,垂线段最短.
13.解:如图所示,∠1和∠2是直线a,c被直线b所截而成的同位角,∠2和∠3是直线a,b被直线c所截而成的同旁内角.
故答案为:同位,同旁内.
14.解:①能与∠DEF构成内错角的角的个数有2个,即∠EFA和∠EDC,故正确;
②能与∠EFB构成同位角的角的个数只有1个:即∠FAE,故正确;
③能与∠C构成同旁内角的角的个数有5个:即∠CDE,∠B,∠CED,∠CEF,∠A,故错误;
所以结论正确的是①②.
故答案为:①②.
15.解:∵OD∥AC,
∴∠BOD'=∠A=70°,
∴∠DOD'=78°﹣70°=8°.
故答案是:8°
16.解:①∵∠1=25.5°+∠ABC=55.5°=∠2=55°30',所以,m∥n;
②没有指明∠1的度数,当∠1≠30°,∠2≠∠1+30°,不能判断直线m∥n,故∠2=2∠1,不能判断直线m∥n;
③∠1+∠2=90°,不能判断直线m∥n;
④∠ACB=∠1+∠2,不能判断直线m∥n;
⑤∠ABC=∠2﹣∠1,判断直线m∥n;
故答案为:①⑤
17.解:∵将一副三角板(∠A=30°)按如图所示方式摆放,使得AB∥EF,
∴∠E=∠EDB=45°,∠B=60°,
∴∠1=45°+60°=105°.
故答案为:105.
18.解:∵AB∥CE,∠B=50°,
∴∠ECD=∠B=50°,
∵CE平分∠ACD,
∴∠ACD=2∠ECD=2×50°=100°,
故答案为:100.
19.解:∵AB∥CD,
∴∠CMF=∠1=57°,
∵MF平分∠CME,
∴∠CME=2∠CMF=114°.
又∵∠CME+∠EMD=180°,
∴∠EMD=180°﹣∠CME=180°﹣114°=66°.
故答案为:66.
20.解:∵∠CEF=∠CHD,
∴DH∥GE,
∴∠ADH=∠G,
∵∠EFC=∠ADH,
∵∠BFG=∠EFC,
∴∠G=∠BFG,
∴∠ABC=∠G+∠BFG=2∠EFC,
∵∠CEF:∠EFC=5:2,∠C=47°,
∴∠EFC=38°,
∴∠ABC=76°,
∵DE∥BC,
∴∠ADE=∠ABC=76°,
故答案为:76°.
三.解答题
21.证明:∵∠1+∠2=180°,∠2+∠AED=180°,
∴∠1=∠AED,
∴DE∥AC,
∴∠D=∠DAF,
∵∠C=∠D,
∴∠DAF=∠C,
∴AD∥BC.
22.证明:∵BF,DE分别平分∠ABC与∠ADC,(已知)
∴∠1=∠ABC,∠2=∠ADC.(角平分线的定义)
∵∠ABC=∠ADC,(已知)
∴∠1=∠2,(等量代换)
∵∠1=∠3,(已知)
∴∠2=∠3.(等量代换)
∴AB∥DC.(内错角相等,两直线平行)
故答案为:角平分线的定义;已知;1,2;已知;3,等量代换;AB,DC,内错角相等,两直线平行.
23.解:∵AB∥CD,∠FGB=154°,
∴∠GFD=180°﹣∠FGB=180°﹣154°=26°,
∵FG平分∠EFD,
∴∠EFD=2∠GFD=2×26°=52°,
∵AB∥CD,
∴∠AEF=∠EFD=52°.
24.解:(1)∵AB∥CD,∴∠MEB=∠MFD,
∵A′E∥C′F,
∴∠MEA′=∠MFC′,
∴∠MEA′﹣∠MEB=∠MFC′﹣∠MFD,
即∠1=∠2;
(2)由折叠知,∠C′FN==70°,
∵A′E∥C′F,
∴∠A′EN=∠C′FN=70°,
∵∠1=∠2,
∴∠BEF=70°+40°=110°.
25.证明:∵AB∥DE,
∴∠B+∠BCE=180°,∠B=∠BCD,
∵CM平分∠BCE,
∴∠1=∠2,
∵CN⊥CM,
∴∠2+∠3=90°,∠1+∠4=90°,
∴∠3=∠4,
∵∠3+∠4=∠BCD,
∴∠B=2∠DCN.
26.解:(1)∵CB∥OA,
∴∠AOC=180°﹣∠C=180°﹣100°=80°,
∵OE平分∠COF,
∴∠COE=∠EOF,
∵∠FOB=∠AOB,
∴∠EOB=∠EOF+∠FOB=∠AOC=×80°=40°;
(2)∵CB∥OA,
∴∠AOB=∠OBC,
∵∠FOB=∠AOB,
∴∠FOB=∠OBC,
∴∠OFC=∠FOB+∠OBC=2∠OBC,
∴∠OBC:∠OFC=1:2,是定值;
(3)在△COE和△AOB中,
∵∠OEC=∠OBA,∠C=∠OAB,
∴∠COE=∠AOB,
∴OB、OE、OF是∠AOC的四等分线,
∴∠COE=∠AOC=×80°=20°,
∴∠OEC=180°﹣∠C﹣∠COE=180°﹣100°﹣20°=60°,
故存在某种情况,使∠OEC=∠OBA,此时∠OEC=∠OBA=60°.
一.选择题
1.在同一平面内,过直线上一点作已知直线的垂线,能作( )
A.1条 B.2条 C.3条 D.无数条
2.如图,小明画了两条直线AB,CD相交于点O,则∠1和∠2是( )
A.对顶角 B.同位角 C.内错角 D.邻补角
3.如图,点E、F分别是AB、CD上的点,点G是BC的延长线上一点,且∠B=∠DCG=∠D,则下列判断不一定成立的是( )
A.AB∥CD B.AD∥BG
C.∠B=∠AEF D.∠BEF+∠EFC=180°
4.如图图形中,∠1和∠2不是同位角的是( )
A. B.
C. D.
5.如图,下列条件中,不能判定l1∥l2的是( )
A.∠1=∠3 B.∠2+∠4=180° C.∠2=∠3 D.∠4+∠5=180°
6.下列各项正确的是( )
A.直线外一点到已知直线的垂线段叫做这点到直线的距离
B.过一点有且只有一条直线与已知直线垂直
C.同一平面内,两条直线的位置关系只有相交和平行两种
D.有公共顶点且相等的两个角是对顶角
7.下列尺规作图的语句错误的是( )
A.作∠AOB,使∠AOB=3∠α
B.以点O为圆心作弧
C.以点A为圆心,线段a的长为半径作弧
D.作∠ABC,使∠ABC=∠α+∠β
8.如图,四边形ABCD中,BC∥AD,CA平分∠BCD,∠1=35°,∠D的度数是( )
A.70° B.130° C.120° D.110°
9.下列各图形中均有直线m∥n,则能使结论∠A=∠1﹣∠2成立的是( )
A. B.
C. D.
10.如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠BED=100°,则∠BFD的度数为( )
A.100° B.130° C.140° D.160°
二.填空题
11.如图,两直线交于点O,∠1=34°,则∠2的度数为 ;∠3的度数为 .
12.如图是小明同学在体育课上跳远后留下的脚印,那么体育陈老师测量小明同学的体育成绩,应该选取线段 的长度,其依据是 .
13.如图,∠1和∠2是 角,∠2和∠3是 角.
14.如图,有下列3个结论:①能与∠DEF构成内错角的角的个数是2;②能与∠EFB构成同位角的角的个数是1;③能与∠C构成同旁内角的角的个数是4,以上结论正确的是 .
15.如图,∠A=70°,O是AB上一点,直线OD与AB所夹的∠BOD=78°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转 .
16.将一块三角板ABC(∠BAC=90°,∠ABC=30°)按如图方式放置,使A,B两点分别落在直线m,n上.对于给出的四个条件:①∠1=25.5°,∠2=55°30';②∠2=2∠1;③∠1+∠2=90°;④∠ACB=∠1+∠2;⑤∠ABC=∠2﹣∠1.能判断直线m∥n的有 .(填序号)
17.将一副三角板(∠A=30°)按如图所示方式摆放,使得AB∥EF,则∠1等于 度.
18.如图,已知AB∥CE,∠B=50°,CE平分∠ACD,则∠ACD= °
19.如图,AB∥CD,点M为CD上一点,MF平分∠CME.若∠1=57°,则∠EMD的大小为 度.
20.如图,三角形ABC中,D是AB上一点,F是BC上一点,E,H是AC上的点,EF的延长线交AB的延长线于点G,连接DE,DH,DE∥BC.若∠CEF=∠CHD,∠EFC=∠ADH,∠CEF:∠EFC=5:2,∠C=47°,则∠ADE的度数为 .
三.解答题
21.如图,∠1+∠2=180°,∠C=∠D.求证:AD∥BC.
22.已知,如图,∠ABC=∠ADC,BF,DE分别平分∠ABC与∠ADC,且∠1=∠3.求证:AB∥DC,请根据条件进行推理,得出结论,并在括号内注明理由.
证明:
∵BF,DE分别平分∠ABC与∠ADC,(已知)
∴∠1=∠ABC,∠2=∠ADC.( )
∵∠ABC=∠ADC,( )
∴∠ =∠ (等量代换)
∵∠1=∠3( )
∴∠2=∠ .( )
∴ ∥ .( )
23.如图,AB∥CD,∠FGB=154°,FG平分∠EFD,求∠AEF的度数.
24.如图,将一张上、下两边平行(即AB∥CD)的纸带沿直线MN折叠,EF为折痕.
(1)试说明∠1=∠2;
(2)已知∠2=40°,求∠BEF的度数.
25.已知:如图,AB∥DE,CM平分∠BCE,CN⊥CM.求证:∠B=2∠DCN.
26.如图,直线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值.
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
参考答案
一.选择题
1.解:在同一平面内,过直线上一点作已知直线的垂线,能作1条.
故选:A.
2.解:由对顶角的定义可知,∠1和∠2是对顶角,
故选:A.
3.解:A、∵∠B=∠DCG=∠D,
∴AB∥DC,AD∥BG,正确,故本选项不符合题意;
B、∵∠B=∠DCG=∠D,
∴AB∥DC,AD∥BG,正确,故本选项不符合题意;
C、根据AB∥DC,AD∥BG不能推出EF∥BC,所以不能推出∠B=∠AEF,错误,故本选项符合题意;
D、∵AB∥CD,
∴∠BEF+∠EFC=180°,正确,故本选项不符合题意;
故选:C.
4.解:∵选项B中∠1和∠2是由四条直线组成,
∴∠1和∠2不是同位角.
故选:B.
5.解:A、∵∠1=∠3,
∴直线l1∥l2,故此选项不合题意;
B、∵∠2+∠4=180°,
∴直线l1∥l2,故此选项不合题意;
C、∠2=∠3,不能得出直线l1∥l2,故此选项符合题意;
D、∵∠2=∠5,4+∠5=180°,
∴4+∠2=180°,
∴直线l1∥l2,故此选项不合题意.
故选:C.
6.解:A、从直线外一点到这条直线的垂线段的长度叫做点到直线的距离,故此选项错误,不合题意;
B、在同一平面内,经过一点能画一条且只能画一条直线与已知直线垂直,故此选项错误,不合题意;
C、同一平面内,两条直线的位置关系只有相交和平行两种,正确,符合题意;
D、有公共顶点且相等的两个角不一定是对顶角,故此选项错误,不合题意.
故选:C.
7.解:A、作一个角等于已知角的倍数是常见的尺规作图,正确;
B、画弧既需要圆心,还需要半径,缺少半径长,错误.
C、以点A为圆心,线段a的长为半径作弧,正确;
D、作∠ABC,使∠ABC=∠α+∠β,正确
故选:B.
8.解:∵BC∥AD,
∴∠1=∠2=35°,
又∵CA平分∠BCD,
∴∠2=∠3=35°,
则∠BCD=70°,
∴∠D=180°﹣∠BCD=180°﹣70°=110°.
故选:D.
9.解:A、∵m∥n,
∴∠2=∠1+∠A,
∴∠A=∠2﹣∠1,不符合题意;
B、∵m∥n,
∴∠1=∠2+∠A,
∴∠A=∠1﹣∠2,符合题意;
C、∵m∥n,
∴∠1+∠2+∠A=360°,
∴∠A=360°﹣∠2﹣∠1,不符合题意;
D、∵m∥n,
∴∠A=∠1+∠2,不符合题意;
故选:B.
10.解:连接BD,
∵AB∥CD,
∴∠ABD+∠CDB=180°,
∴∠ABE+∠E+∠CDE=180°+180°=360°,
∴∠ABE+∠CDE=360°﹣100°=260°,
又∵BF、DF平分∠ABE和∠CDE,
∴∠FBE+∠FDE=130°,
∴∠BFD=360°﹣100°﹣130°=130°.
故选:B.
二.填空题
11.解:∵∠1=34°,∠1+∠2=180°,
∴∠2=180°﹣∠1=180°﹣34°=146°,
∵∠1与∠3是对顶角,∠1=34°,
∴∠3=∠1=34°.
故答案为:146°,34°.
12.解:小明同学的体育成绩,应该选取线段CD的长度.依据为:垂线段最短.
故答案为:CD,垂线段最短.
13.解:如图所示,∠1和∠2是直线a,c被直线b所截而成的同位角,∠2和∠3是直线a,b被直线c所截而成的同旁内角.
故答案为:同位,同旁内.
14.解:①能与∠DEF构成内错角的角的个数有2个,即∠EFA和∠EDC,故正确;
②能与∠EFB构成同位角的角的个数只有1个:即∠FAE,故正确;
③能与∠C构成同旁内角的角的个数有5个:即∠CDE,∠B,∠CED,∠CEF,∠A,故错误;
所以结论正确的是①②.
故答案为:①②.
15.解:∵OD∥AC,
∴∠BOD'=∠A=70°,
∴∠DOD'=78°﹣70°=8°.
故答案是:8°
16.解:①∵∠1=25.5°+∠ABC=55.5°=∠2=55°30',所以,m∥n;
②没有指明∠1的度数,当∠1≠30°,∠2≠∠1+30°,不能判断直线m∥n,故∠2=2∠1,不能判断直线m∥n;
③∠1+∠2=90°,不能判断直线m∥n;
④∠ACB=∠1+∠2,不能判断直线m∥n;
⑤∠ABC=∠2﹣∠1,判断直线m∥n;
故答案为:①⑤
17.解:∵将一副三角板(∠A=30°)按如图所示方式摆放,使得AB∥EF,
∴∠E=∠EDB=45°,∠B=60°,
∴∠1=45°+60°=105°.
故答案为:105.
18.解:∵AB∥CE,∠B=50°,
∴∠ECD=∠B=50°,
∵CE平分∠ACD,
∴∠ACD=2∠ECD=2×50°=100°,
故答案为:100.
19.解:∵AB∥CD,
∴∠CMF=∠1=57°,
∵MF平分∠CME,
∴∠CME=2∠CMF=114°.
又∵∠CME+∠EMD=180°,
∴∠EMD=180°﹣∠CME=180°﹣114°=66°.
故答案为:66.
20.解:∵∠CEF=∠CHD,
∴DH∥GE,
∴∠ADH=∠G,
∵∠EFC=∠ADH,
∵∠BFG=∠EFC,
∴∠G=∠BFG,
∴∠ABC=∠G+∠BFG=2∠EFC,
∵∠CEF:∠EFC=5:2,∠C=47°,
∴∠EFC=38°,
∴∠ABC=76°,
∵DE∥BC,
∴∠ADE=∠ABC=76°,
故答案为:76°.
三.解答题
21.证明:∵∠1+∠2=180°,∠2+∠AED=180°,
∴∠1=∠AED,
∴DE∥AC,
∴∠D=∠DAF,
∵∠C=∠D,
∴∠DAF=∠C,
∴AD∥BC.
22.证明:∵BF,DE分别平分∠ABC与∠ADC,(已知)
∴∠1=∠ABC,∠2=∠ADC.(角平分线的定义)
∵∠ABC=∠ADC,(已知)
∴∠1=∠2,(等量代换)
∵∠1=∠3,(已知)
∴∠2=∠3.(等量代换)
∴AB∥DC.(内错角相等,两直线平行)
故答案为:角平分线的定义;已知;1,2;已知;3,等量代换;AB,DC,内错角相等,两直线平行.
23.解:∵AB∥CD,∠FGB=154°,
∴∠GFD=180°﹣∠FGB=180°﹣154°=26°,
∵FG平分∠EFD,
∴∠EFD=2∠GFD=2×26°=52°,
∵AB∥CD,
∴∠AEF=∠EFD=52°.
24.解:(1)∵AB∥CD,∴∠MEB=∠MFD,
∵A′E∥C′F,
∴∠MEA′=∠MFC′,
∴∠MEA′﹣∠MEB=∠MFC′﹣∠MFD,
即∠1=∠2;
(2)由折叠知,∠C′FN==70°,
∵A′E∥C′F,
∴∠A′EN=∠C′FN=70°,
∵∠1=∠2,
∴∠BEF=70°+40°=110°.
25.证明:∵AB∥DE,
∴∠B+∠BCE=180°,∠B=∠BCD,
∵CM平分∠BCE,
∴∠1=∠2,
∵CN⊥CM,
∴∠2+∠3=90°,∠1+∠4=90°,
∴∠3=∠4,
∵∠3+∠4=∠BCD,
∴∠B=2∠DCN.
26.解:(1)∵CB∥OA,
∴∠AOC=180°﹣∠C=180°﹣100°=80°,
∵OE平分∠COF,
∴∠COE=∠EOF,
∵∠FOB=∠AOB,
∴∠EOB=∠EOF+∠FOB=∠AOC=×80°=40°;
(2)∵CB∥OA,
∴∠AOB=∠OBC,
∵∠FOB=∠AOB,
∴∠FOB=∠OBC,
∴∠OFC=∠FOB+∠OBC=2∠OBC,
∴∠OBC:∠OFC=1:2,是定值;
(3)在△COE和△AOB中,
∵∠OEC=∠OBA,∠C=∠OAB,
∴∠COE=∠AOB,
∴OB、OE、OF是∠AOC的四等分线,
∴∠COE=∠AOC=×80°=20°,
∴∠OEC=180°﹣∠C﹣∠COE=180°﹣100°﹣20°=60°,
故存在某种情况,使∠OEC=∠OBA,此时∠OEC=∠OBA=60°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
