广西钦州第四高级中学校2020-2021学年高一下学期3月第四周周测数学试题 Word版含答案
文档属性
| 名称 | 广西钦州第四高级中学校2020-2021学年高一下学期3月第四周周测数学试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 251.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 15:05:32 | ||
图片预览



文档简介
广西钦州市第四中学2021年春季学期高一数学第四周周测试卷一.选择题
1.在空间,已知直线l及不在l上两个不重合的点A、B,过直线l做平面α,使得点A、B到平面α的距离相等,则这样的平面α的个数不可能是( )
A.1个 B.2个 C.3个 D.无数个
2.下列命题中正确的是( )
A.三点确定一个平面 B.垂直于同一直线的两条直线平行
C.若直线l与平面α上的无数条直线都垂直,则直线l⊥α
D.若a、b、c是三条直线,a∥b且与c都相交,则直线a、b、c共面
3.已知m,n是空间中两条不同的直线,α,β为空间中两个不同的平面.
①若m?α,α⊥β,则m⊥β;②若m⊥α,m∥n,n∥β,则α⊥β;
③若m⊥β,n⊥β,n⊥α,则m⊥α;④若m⊥α,m⊥n,则n∥α;
⑤若α∥β,m?α,n?β,则m∥n.
则以上说法正确的是( )
A.①⑤ B.②③④ C.②③ D.①②④⑤
4.在四棱锥P﹣ABCD中,PC⊥平面ABCD,∠ABC=∠DCB=90°,∠PBC=30°,AB=2PC=4CD,E是PA的中点,则异面直线BE与AD所成的角为( )
A.30° B.45° C.60° D.90°
5.在直四棱柱ABCD﹣A1B1C1D1中,四边形ABCD为菱形,且AB=AA1=AC,点E,F分别为AD,CD的中点,则异面直线EF,BC1所成角的大小为( )
A.30° B.45° C.60° D.90°
6.类比平面内“垂直于同一条直线的两条直线互相平行”的性质,可推出空间中有下列结论:
①垂直于同一条直线的两条直线互相平行;
②垂直于同一条直线的两个平面互相平行;
③垂直于同一个平面的两条直线互相平行;
④垂直于同一个平面的两个平面互相平行.
其中正确的是( )
A.①② B.①④ C.②③ D.③④
7.已知两条异面直线的方向向量分别是=(3,1,﹣2),=(3,2,1),则这两条异面直线所成的角θ满足( )
A.sinθ= B.sinθ= C.cosθ= D.cosθ=
8.在棱长为1的正方体ABCD﹣A'B'C'D'中,已知点P是正方形AA'D'D内部(不含边界)的一个动点,若直线AP与平面AA'B'B所成角的正弦值和异面直线AP与DC'所成角的余弦值相等,则线段DP长度的最小值是( )
A. B. C. D.
9.已知m,n表示两条不同直线,α表示平面,下列说法正确的是( )
A.若m∥n,m∥α,则n∥α B.若m⊥n,n?α,则m⊥α
C.若m⊥α,m⊥n,则n∥α D.若m∥α,n⊥α,则m⊥n
10.正方体上的点P、Q、R、S是其所在棱的中点,则直线PQ与直线RS异面的图形是( )
A. B.
C. D.
11.如图,在正方体ABCD﹣A1B1C1D1中,点O,M,N分别是线段BD,DD1,D1C1的中点,则直线OM与AC,MN的位置关系是( )
A.与AC,MN均垂直 B.与AC垂直,与MN不垂直
C.与AC不垂直,与MN垂直 D.与AC,MN均不垂直
12.已知二面角α﹣l﹣β的大小为60°,A,B为棱l上不同两点,C,D分别在半平面α,β内,AC,BD均垂直于棱l,AC=BD=2AB=2,则异面直线CD与AB所成角的余弦值为( )
A. B. C. D.
二.填空题
13.三个不相交的平面把空间分成 部分.
14.设=(2,2,﹣),=(0,﹣1,)分别是空间中直线l1,l2的方向向量,则直线l1,l2所成角的余弦值为 .
15.已知直线m∥平面α,直线n在α内,则m与n所有可能的位置关系是 .
16.已知直三棱柱ABC﹣A1B1C1中,∠ABC=90°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的正弦值为 .
三.解答题
17.如图,直三棱柱A1B1C1﹣ABC中,AB=AC=1,,A1A=4,点M为线段A1A的中点.
(1)求直三棱柱A1B1C1﹣ABC的体积;
(2)求异面直线BM与B1C1所成的角的大小.(结果用反三角表示)
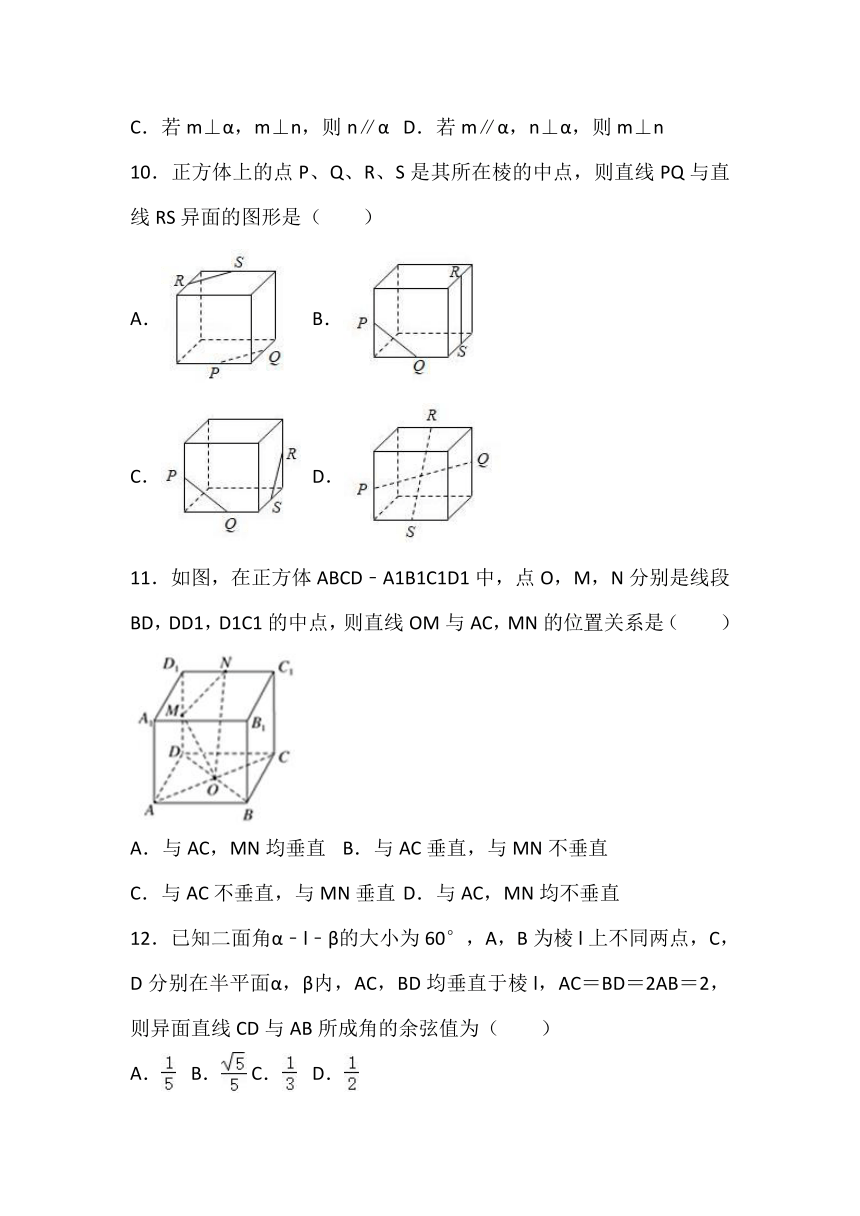
18.如图,正四棱柱ABCD﹣A1B1C1D1的底面边长为2,A1D=4.
(1)求该正四棱柱的表面积和体积;
(2)求异面直线A1D与AC所成的角的大小(结果用反三角函数值表示).
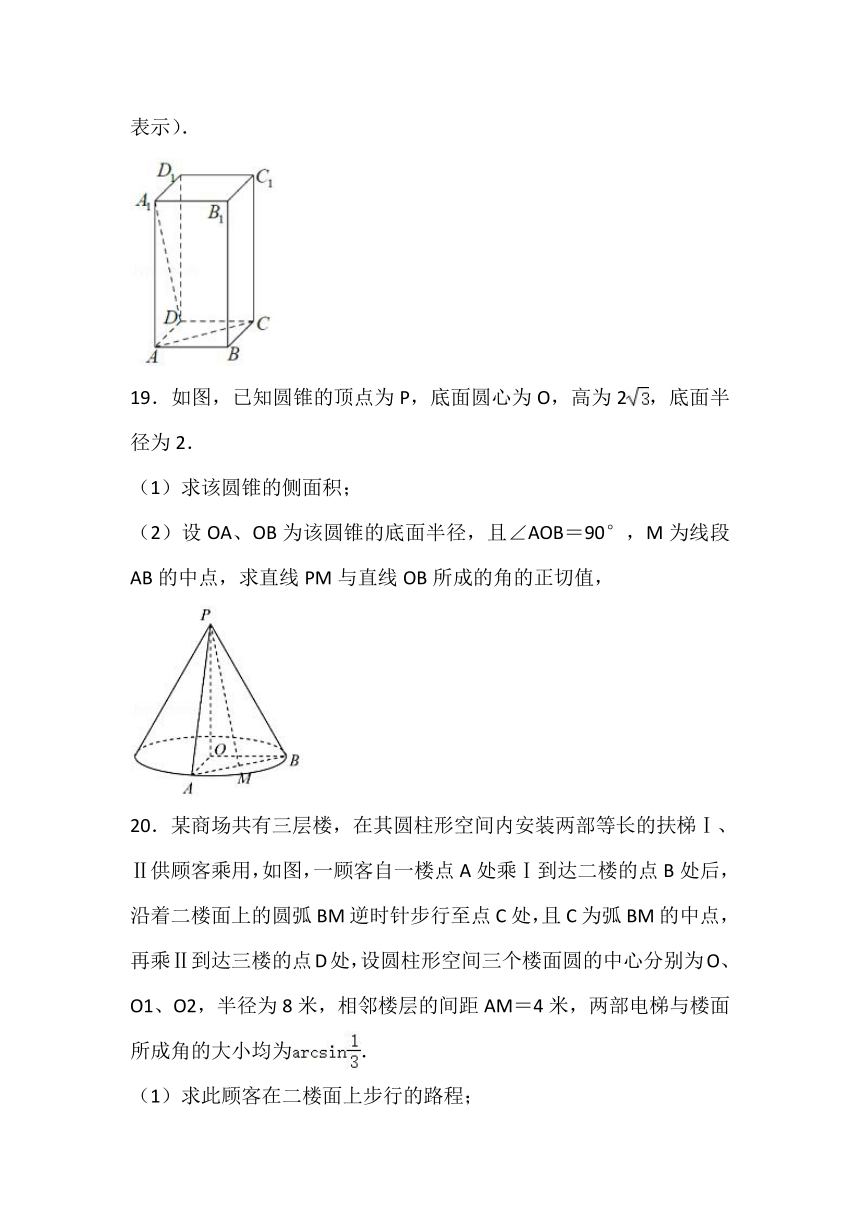
19.如图,已知圆锥的顶点为P,底面圆心为O,高为2,底面半径为2.
(1)求该圆锥的侧面积;
(2)设OA、OB为该圆锥的底面半径,且∠AOB=90°,M为线段AB的中点,求直线PM与直线OB所成的角的正切值,
20.某商场共有三层楼,在其圆柱形空间内安装两部等长的扶梯Ⅰ、Ⅱ供顾客乘用,如图,一顾客自一楼点A处乘Ⅰ到达二楼的点B处后,沿着二楼面上的圆弧BM逆时针步行至点C处,且C为弧BM的中点,再乘Ⅱ到达三楼的点D处,设圆柱形空间三个楼面圆的中心分别为O、O1、O2,半径为8米,相邻楼层的间距AM=4米,两部电梯与楼面所成角的大小均为.
(1)求此顾客在二楼面上步行的路程;
(2)求异面直线AB和CD所成角的大小.(结果用反三角函数值表示)
参考答案
一.选择题
1.C
2.D
3.C
4.D
5.C
6.C
7.C
8.C
9.D
10.B
11.A
12.B
二.填空题
13.4
14..
15.平行或异面.
16..
三.解答题
17.解:(1)∵,
∴V=S△ABC?A1A=×4=2.
(2)∵BC∥B1C1,
∴∠MBC或其补角是异面直线BM与B1C1所成的角,
在△MBC中,BM=CM=,BC=,
由余弦定理得,cos∠MBC==,
∴∠MBC=arccos,
故异面直线BM与B1C1所成的角为.
18.解:(1)由题意,得=,
则该正四棱柱的表面积为=8+16,
该正四棱柱的体积为V==8.
(2)连接A1C1,DC1,则AC∥A1C1,
∴直线A1D,A1C1所成角就是异面直线A1D,AC所成角,
在△A1DC1中,A1D=DC1=2,A1C1=2,
由余弦定理得cos∠DA1C1=
==.
∴异面直线A1D与AC所成的角的大小为arccos.
19.解:(1)由题意知,h=,r=2,
∴圆锥的母线l==4,
∴圆锥的侧面积S=l?2πr=×4×2π×2=8π.
(2)取OA的中点N,连接MN,PN,
∵M为AB的中点,
∴MN∥OB,
∴∠PMN或其补角即为直线PM与直线OB所成的角,
∵OB⊥OA,OB⊥OP,OA∩OP=O,OA、OP?平面POA,
∴OB⊥平面POA,
∴MN⊥平面POA,∴MN⊥PN,
在Rt△PMN中,PN==,MN=OB=1,
∴tan∠PMN==,
故直线PM与直线OB所成的角的正切值为.
20.解:(1)过点B作1楼面的垂线,垂足是B′,
则B′落在圆柱底面圆上,连接B′A,
则B′A即为BA在圆柱下底面上的射影,
故∠BAB′即为BA与楼面所成的角,即∠BAB′=arcsin,
BB′=AM=4,可得AB=8,△AOB中,OA=OB′=8,
故△AOB′是等腰直角三角形,故∠BO1M=∠AOB′=,
∵AB=CD,故弧BC的长为8×=2π,
故此顾客在二楼面上步行的路程为2π米;
(2)由(1)可知OA,OB′,OO2两两互相垂直相交,
于是以O为坐标原点,以射线OB′,OA,OO2分别为x,y,z轴建立空间直角坐标系,
如图示:
则B(8,0,4),A(0,8,0),C(4,4,4),D(﹣4,4,8),
故=(8,﹣8,4),=(﹣8,0,4),
设异面直线AB和CD所成角的大小为θ,
则cosθ==>0,
即θ=arccos,
故异面直线AB和CD所成角的大小为arccos.
1.在空间,已知直线l及不在l上两个不重合的点A、B,过直线l做平面α,使得点A、B到平面α的距离相等,则这样的平面α的个数不可能是( )
A.1个 B.2个 C.3个 D.无数个
2.下列命题中正确的是( )
A.三点确定一个平面 B.垂直于同一直线的两条直线平行
C.若直线l与平面α上的无数条直线都垂直,则直线l⊥α
D.若a、b、c是三条直线,a∥b且与c都相交,则直线a、b、c共面
3.已知m,n是空间中两条不同的直线,α,β为空间中两个不同的平面.
①若m?α,α⊥β,则m⊥β;②若m⊥α,m∥n,n∥β,则α⊥β;
③若m⊥β,n⊥β,n⊥α,则m⊥α;④若m⊥α,m⊥n,则n∥α;
⑤若α∥β,m?α,n?β,则m∥n.
则以上说法正确的是( )
A.①⑤ B.②③④ C.②③ D.①②④⑤
4.在四棱锥P﹣ABCD中,PC⊥平面ABCD,∠ABC=∠DCB=90°,∠PBC=30°,AB=2PC=4CD,E是PA的中点,则异面直线BE与AD所成的角为( )
A.30° B.45° C.60° D.90°
5.在直四棱柱ABCD﹣A1B1C1D1中,四边形ABCD为菱形,且AB=AA1=AC,点E,F分别为AD,CD的中点,则异面直线EF,BC1所成角的大小为( )
A.30° B.45° C.60° D.90°
6.类比平面内“垂直于同一条直线的两条直线互相平行”的性质,可推出空间中有下列结论:
①垂直于同一条直线的两条直线互相平行;
②垂直于同一条直线的两个平面互相平行;
③垂直于同一个平面的两条直线互相平行;
④垂直于同一个平面的两个平面互相平行.
其中正确的是( )
A.①② B.①④ C.②③ D.③④
7.已知两条异面直线的方向向量分别是=(3,1,﹣2),=(3,2,1),则这两条异面直线所成的角θ满足( )
A.sinθ= B.sinθ= C.cosθ= D.cosθ=
8.在棱长为1的正方体ABCD﹣A'B'C'D'中,已知点P是正方形AA'D'D内部(不含边界)的一个动点,若直线AP与平面AA'B'B所成角的正弦值和异面直线AP与DC'所成角的余弦值相等,则线段DP长度的最小值是( )
A. B. C. D.
9.已知m,n表示两条不同直线,α表示平面,下列说法正确的是( )
A.若m∥n,m∥α,则n∥α B.若m⊥n,n?α,则m⊥α
C.若m⊥α,m⊥n,则n∥α D.若m∥α,n⊥α,则m⊥n
10.正方体上的点P、Q、R、S是其所在棱的中点,则直线PQ与直线RS异面的图形是( )
A. B.
C. D.
11.如图,在正方体ABCD﹣A1B1C1D1中,点O,M,N分别是线段BD,DD1,D1C1的中点,则直线OM与AC,MN的位置关系是( )
A.与AC,MN均垂直 B.与AC垂直,与MN不垂直
C.与AC不垂直,与MN垂直 D.与AC,MN均不垂直
12.已知二面角α﹣l﹣β的大小为60°,A,B为棱l上不同两点,C,D分别在半平面α,β内,AC,BD均垂直于棱l,AC=BD=2AB=2,则异面直线CD与AB所成角的余弦值为( )
A. B. C. D.
二.填空题
13.三个不相交的平面把空间分成 部分.
14.设=(2,2,﹣),=(0,﹣1,)分别是空间中直线l1,l2的方向向量,则直线l1,l2所成角的余弦值为 .
15.已知直线m∥平面α,直线n在α内,则m与n所有可能的位置关系是 .
16.已知直三棱柱ABC﹣A1B1C1中,∠ABC=90°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的正弦值为 .
三.解答题
17.如图,直三棱柱A1B1C1﹣ABC中,AB=AC=1,,A1A=4,点M为线段A1A的中点.
(1)求直三棱柱A1B1C1﹣ABC的体积;
(2)求异面直线BM与B1C1所成的角的大小.(结果用反三角表示)
18.如图,正四棱柱ABCD﹣A1B1C1D1的底面边长为2,A1D=4.
(1)求该正四棱柱的表面积和体积;
(2)求异面直线A1D与AC所成的角的大小(结果用反三角函数值表示).
19.如图,已知圆锥的顶点为P,底面圆心为O,高为2,底面半径为2.
(1)求该圆锥的侧面积;
(2)设OA、OB为该圆锥的底面半径,且∠AOB=90°,M为线段AB的中点,求直线PM与直线OB所成的角的正切值,
20.某商场共有三层楼,在其圆柱形空间内安装两部等长的扶梯Ⅰ、Ⅱ供顾客乘用,如图,一顾客自一楼点A处乘Ⅰ到达二楼的点B处后,沿着二楼面上的圆弧BM逆时针步行至点C处,且C为弧BM的中点,再乘Ⅱ到达三楼的点D处,设圆柱形空间三个楼面圆的中心分别为O、O1、O2,半径为8米,相邻楼层的间距AM=4米,两部电梯与楼面所成角的大小均为.
(1)求此顾客在二楼面上步行的路程;
(2)求异面直线AB和CD所成角的大小.(结果用反三角函数值表示)
参考答案
一.选择题
1.C
2.D
3.C
4.D
5.C
6.C
7.C
8.C
9.D
10.B
11.A
12.B
二.填空题
13.4
14..
15.平行或异面.
16..
三.解答题
17.解:(1)∵,
∴V=S△ABC?A1A=×4=2.
(2)∵BC∥B1C1,
∴∠MBC或其补角是异面直线BM与B1C1所成的角,
在△MBC中,BM=CM=,BC=,
由余弦定理得,cos∠MBC==,
∴∠MBC=arccos,
故异面直线BM与B1C1所成的角为.
18.解:(1)由题意,得=,
则该正四棱柱的表面积为=8+16,
该正四棱柱的体积为V==8.
(2)连接A1C1,DC1,则AC∥A1C1,
∴直线A1D,A1C1所成角就是异面直线A1D,AC所成角,
在△A1DC1中,A1D=DC1=2,A1C1=2,
由余弦定理得cos∠DA1C1=
==.
∴异面直线A1D与AC所成的角的大小为arccos.
19.解:(1)由题意知,h=,r=2,
∴圆锥的母线l==4,
∴圆锥的侧面积S=l?2πr=×4×2π×2=8π.
(2)取OA的中点N,连接MN,PN,
∵M为AB的中点,
∴MN∥OB,
∴∠PMN或其补角即为直线PM与直线OB所成的角,
∵OB⊥OA,OB⊥OP,OA∩OP=O,OA、OP?平面POA,
∴OB⊥平面POA,
∴MN⊥平面POA,∴MN⊥PN,
在Rt△PMN中,PN==,MN=OB=1,
∴tan∠PMN==,
故直线PM与直线OB所成的角的正切值为.
20.解:(1)过点B作1楼面的垂线,垂足是B′,
则B′落在圆柱底面圆上,连接B′A,
则B′A即为BA在圆柱下底面上的射影,
故∠BAB′即为BA与楼面所成的角,即∠BAB′=arcsin,
BB′=AM=4,可得AB=8,△AOB中,OA=OB′=8,
故△AOB′是等腰直角三角形,故∠BO1M=∠AOB′=,
∵AB=CD,故弧BC的长为8×=2π,
故此顾客在二楼面上步行的路程为2π米;
(2)由(1)可知OA,OB′,OO2两两互相垂直相交,
于是以O为坐标原点,以射线OB′,OA,OO2分别为x,y,z轴建立空间直角坐标系,
如图示:
则B(8,0,4),A(0,8,0),C(4,4,4),D(﹣4,4,8),
故=(8,﹣8,4),=(﹣8,0,4),
设异面直线AB和CD所成角的大小为θ,
则cosθ==>0,
即θ=arccos,
故异面直线AB和CD所成角的大小为arccos.
同课章节目录
