19.3课题学习方案选择 课件(共34张PPT)
文档属性
| 名称 | 19.3课题学习方案选择 课件(共34张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 854.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 17:25:50 | ||
图片预览











文档简介
19.3课题学习方案选择
第十九章 一次函数
2021年春人教版八年级(下)数学
某单位要制作一批宣传材料.甲公司提出:每份材料收费20元,另收3000元设计费;乙公司提出:每份材料收费30元,不收设计费.
让哪家公司制作这批宣传材料比较合算?
这节课我们结合这个问题来学习怎样选择最佳方案.
新课导入
(1)能熟练列函数关系式表示实际问题中的数量关系.
(2)能运用一次函数的知识帮助分析、确定和选择最佳方案.
重点:运用一次函数的知识确定最佳方案.
难点:在不同情况下对自变量x的范围的确定.
学习目标
思考两家公司收费额的计算方法,列出相应的函数关系式.
某单位要制作一批宣传材料.甲公司提出:每份材料收费20元,另收3000元设计费;乙公司提出:每份材料收费30元,不收设计费.
宣传材料制作的收费问题
探究新知
思考:两家公司的收费都与什么有关?
两家公司的收费都与材料的份数有关
探究新知
设共有x份材料,两家公司的收费分别为y1(元)、y2(元),则有:
y1=20x+3000,y2=30x;
当y1>y2时,x<300;
当y1=y2时,x=300;
当y1<y2时,x>300.
由此可以看出,选取哪家公司付费y元是由材料的份数x决定的.
探究新知
宽带收费问题
探
究
怎样选取上网收费方式?
下表给出A,B,C 三种上宽带网的收费方式:
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
选取哪种方式能节省上网费?
该问题要我们做什么?选择方案的依据是什么?
探究新知
思
考
在A,B两种方式中,影响上网费用的变量是 ,方式C中的上网费用是 .
上网时间
常量
A,B,C三种收费方式的函数表达式分别是什么?
探究新知
设月上网时间为xh,方案A,方案B,方案C的收费金额分别为y1,y2,y3,则有:
方案A费用:
y1=
30, 0≤t≤25;
3t-45, t>25.
方案B费用:
y2=
50, 0≤t≤50;
3t-100,t>50.
方案C费用:
y3=120.
探究新知
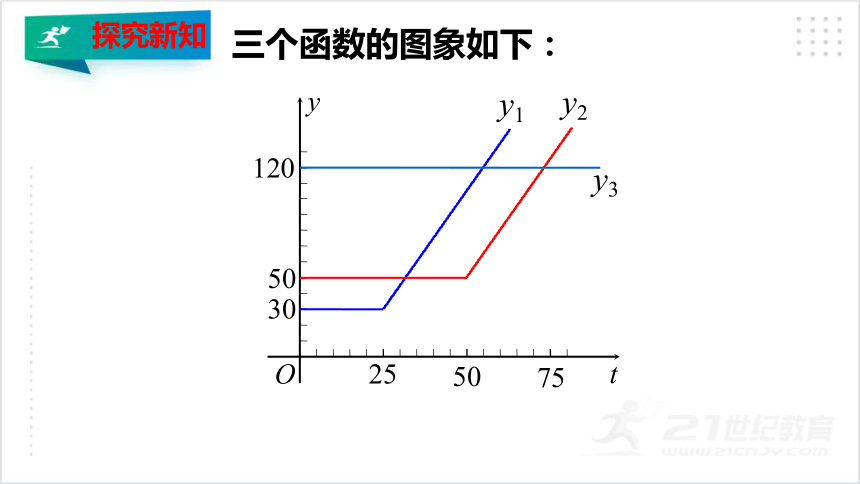
三个函数的图象如下:
120
50
30
25
50
75
O
t
y
y1
y2
y3
探究新知
120
50
30
25
50
75
O
t
y
y1
y2
y3
由函数图象可知:
31小时40分
73小时20分
(1)当上网时间不超过 ,选择方案A最省钱;
31小时40分
(2)当上网时间为 ,选择方案B最省钱;
31小时40分至73小时20分
(3)当上网时间 ,选择方案C最省钱.
超过73小时20分
探究新知
停车场汽车停放的收费问题
(1)写出国庆节这天停车场的收费金额y元与小车停放辆次x辆之间的函数关系式,并指出自变量的取值范围;
某汽车停车场预计“十一”国庆节这一天将停放大小汽车1200辆次,该停车场的收费标准为:大车每辆次10元,小车每辆次5元.根据预计,解答下面的问题:
探究新知
用x表示小车停放辆次,
则大车停放的次数为1200-x.
收费金额y关于x的解析式为:y=-5x+12000.
自变量的取值范围是0≤x≤1200.
探究新知
(2)如果国庆节这天停放的小车辆次占总停车辆次的65%—85%,请你估计国庆节这天该停车场收费金额的范围.
估计国庆节这天该停车场收费金额的范围是由什么来确定?
小车停放辆次
探究新知
租车问题
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有1名教师.现在有甲、乙两种大客车,它们的载客量和租金如下表:
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}
甲种客车
乙种客车
载客量/(人/辆)
45
30
租金/(元/辆)
400
280
探究新知
(1)共需租多少辆汽车?
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}
甲种客车
乙种客车
载客量/(人/辆)
45
30
租金/(元/辆)
400
280
分析:
①要保证240名师生有车坐.
②要使每辆汽车上至少要有1名教师
根据①可知,汽车总数不能小于____;
根据②可知,汽车总数不能大于____.
综合起来可知汽车总数为 .
6
6
6
探究新知
租车费用与租车种类有关.设租用x辆甲种客车,则租车费用y(单位:元)是 x 的函数,即 :
y=400x+280(6-x)
化简为: y=120x+1680
(2)给出最节省费用的租车方案.
探究新知
在考虑上述问题的基础上,你能得出几种不同的租车方案?为节省费用应选择其中的哪种方案?试说明理由.
4两甲种客车,2两乙种客车;
5两甲种客车,1辆乙种客车;
y1=120×4+1680=2160
y2=120×5+1680=2280
应选择方案一,它比方案二节约120元.
方案一
方案二
探究新知
归
纳
解决含有多个变量的问题时,可以分析这些变量之间的关系,从中选取一个取值能影响其他变量的值的变量作为自变量.然后根据问题的条件寻求可以反映实际问题的函数,以此作为解决问题的数学模型.
归纳小结
选择方案的基本步骤
1.理解题意并建立函数模型;
2.利用不等式(组)或方程(组)确定自变量的取值范围或取值;
3.结合实际确定最佳方案.
归纳小结
1.某商店需要购进一批电视机和洗衣机,根据市场调查,决定电视机进货量不少于洗衣机进货量的一半.电视机与洗衣机的进价和售价如下表:
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}类别
电视机
洗衣机
进价(元/台)
1800
1500
售价(元/台)
2000
1600
计划购进电视机和洗衣机共100台,商店最多可筹集资金161800元.
课堂练习
(1)请你帮助商店算一算有多少种进货方案?(不考虑除进价之外的其他费用)
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}类别
电视机
洗衣机
进价(元/台)
1800
1500
售价(元/台)
2000
1600
解:设电视机进货x台,则洗衣机进货(100-x)台.
则由题意得:1800x+1500×(100-x)≤161800.
解得x≤39.
又∵x≥ (100-x),∴x≥34,∴34≤x≤39.
∴商店一共有6种进货方案.
课堂练习
(2)哪种进货方案待商店销售购进的电视机与洗衣机完毕后获得利润最多?并求出最多利润.(利润=售价-进价)
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}类别
电视机
洗衣机
进价(元/台)
1800
1500
售价(元/台)
2000
1600
课堂练习
设利润为y元,则由题意得:
y=(2000-1800)·x+(1600-1500)(100-x)
=100x+10000.
∵34≤x≤39,
∴当x=39时,ymax=100×39+10000=13900.
∴当商店购进电视机39台、洗衣机61台时,获得的利润最多,为13900元.
课堂练习
2. 某饮料厂为了开发新产品,现有A、B两种果汁原料各19千克、17.2千克,试制甲、乙两种新型饮料50千克,下表是实验的相关数据:
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}
甲
乙
A(单位:千克)
0.5
0.2
B(单位:千克)
0.3
0.4
类别
每千克含量
课堂练习
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}
甲
乙
A(单位:千克)
0.5
0.2
B(单位:千克)
0.3
0.4
(1)假设甲种饮料需配制x千克,请你写出满足题意的不等式组,并求出其解集;
类别
每千克含量
解:
解集为28≤x≤30.
0.5x+(50-x)×0.2≤19,
0.3x+(50-x) ×0.4≤17.2
课堂练习
(2)设甲种饮料每千克成本为4元,乙种饮料每千克成本为3元,这两种饮料的成本总额为y元,请写出y关于x的函数表达式.根据(1)的运算结果,确定当甲种饮料配制多少千克时,甲、乙两种饮料的成本总额最少?
y关于x的函数表达式为:y=4x+(50-x)×3=x+150.
∵28≤x≤30,∴当x=28时,ymin=28+150=178.
∴当甲种饮料配制28千克时,甲、乙两种饮料的成本总额最少,为178元.
课堂练习
3.康乐公司在A、B两地分别有同型号的机器17台和15台,现要运往甲地18台,乙地14台.从A、B两地运往甲、乙两地的费用如下表:
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}
甲地(元/台)
乙地(元/台)
A地
600
500
B地
400
800
目的地
出发地
课堂练习
解:如果从A地运往甲地x台,则从A地运往乙地(17-x)台,从B地运往甲地(18-x)台,从B地运往乙地(x-3)台.
则由题意得:y=600x+500×(17-x)+400×(18-x)+800×(x-3)=500x+13300.
(1)如果从A地运往甲地x台,求完成以上调运所需总费用y(元)关于x(台)的函数关系式;
课堂练习
∴完成以上调运所需总费用y(元)关于x(台)的函数关系式为y=500x+13300(3≤x≤17).
x≥0
x-3≥0
17-x≥0
18-x≥0
∵
解得3≤x≤17.
课堂练习
∵3≤x≤17,
∴当x=3时,ymin=500×3+13300=14800.
∴当从A地运3台机器到甲地,运14台到乙地,从B地运15台到甲地时,所需的总费用最少,为14800元.
(2)若康乐公司请你设计一种最佳调运方案,使总费用最少,则该公司完成以上调运方案至少需要多少费用?
课堂练习
选择方案的基本步骤
1.理解题意并建立函数模型;
2.利用不等式(组)或方程(组)确定自变量的取值范围或取值;
3.结合实际确定最佳方案.
课堂小结
https://www.21cnjy.com/help/help_extract.php
第十九章 一次函数
2021年春人教版八年级(下)数学
某单位要制作一批宣传材料.甲公司提出:每份材料收费20元,另收3000元设计费;乙公司提出:每份材料收费30元,不收设计费.
让哪家公司制作这批宣传材料比较合算?
这节课我们结合这个问题来学习怎样选择最佳方案.
新课导入
(1)能熟练列函数关系式表示实际问题中的数量关系.
(2)能运用一次函数的知识帮助分析、确定和选择最佳方案.
重点:运用一次函数的知识确定最佳方案.
难点:在不同情况下对自变量x的范围的确定.
学习目标
思考两家公司收费额的计算方法,列出相应的函数关系式.
某单位要制作一批宣传材料.甲公司提出:每份材料收费20元,另收3000元设计费;乙公司提出:每份材料收费30元,不收设计费.
宣传材料制作的收费问题
探究新知
思考:两家公司的收费都与什么有关?
两家公司的收费都与材料的份数有关
探究新知
设共有x份材料,两家公司的收费分别为y1(元)、y2(元),则有:
y1=20x+3000,y2=30x;
当y1>y2时,x<300;
当y1=y2时,x=300;
当y1<y2时,x>300.
由此可以看出,选取哪家公司付费y元是由材料的份数x决定的.
探究新知
宽带收费问题
探
究
怎样选取上网收费方式?
下表给出A,B,C 三种上宽带网的收费方式:
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
选取哪种方式能节省上网费?
该问题要我们做什么?选择方案的依据是什么?
探究新知
思
考
在A,B两种方式中,影响上网费用的变量是 ,方式C中的上网费用是 .
上网时间
常量
A,B,C三种收费方式的函数表达式分别是什么?
探究新知
设月上网时间为xh,方案A,方案B,方案C的收费金额分别为y1,y2,y3,则有:
方案A费用:
y1=
30, 0≤t≤25;
3t-45, t>25.
方案B费用:
y2=
50, 0≤t≤50;
3t-100,t>50.
方案C费用:
y3=120.
探究新知
三个函数的图象如下:
120
50
30
25
50
75
O
t
y
y1
y2
y3
探究新知
120
50
30
25
50
75
O
t
y
y1
y2
y3
由函数图象可知:
31小时40分
73小时20分
(1)当上网时间不超过 ,选择方案A最省钱;
31小时40分
(2)当上网时间为 ,选择方案B最省钱;
31小时40分至73小时20分
(3)当上网时间 ,选择方案C最省钱.
超过73小时20分
探究新知
停车场汽车停放的收费问题
(1)写出国庆节这天停车场的收费金额y元与小车停放辆次x辆之间的函数关系式,并指出自变量的取值范围;
某汽车停车场预计“十一”国庆节这一天将停放大小汽车1200辆次,该停车场的收费标准为:大车每辆次10元,小车每辆次5元.根据预计,解答下面的问题:
探究新知
用x表示小车停放辆次,
则大车停放的次数为1200-x.
收费金额y关于x的解析式为:y=-5x+12000.
自变量的取值范围是0≤x≤1200.
探究新知
(2)如果国庆节这天停放的小车辆次占总停车辆次的65%—85%,请你估计国庆节这天该停车场收费金额的范围.
估计国庆节这天该停车场收费金额的范围是由什么来确定?
小车停放辆次
探究新知
租车问题
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有1名教师.现在有甲、乙两种大客车,它们的载客量和租金如下表:
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}
甲种客车
乙种客车
载客量/(人/辆)
45
30
租金/(元/辆)
400
280
探究新知
(1)共需租多少辆汽车?
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}
甲种客车
乙种客车
载客量/(人/辆)
45
30
租金/(元/辆)
400
280
分析:
①要保证240名师生有车坐.
②要使每辆汽车上至少要有1名教师
根据①可知,汽车总数不能小于____;
根据②可知,汽车总数不能大于____.
综合起来可知汽车总数为 .
6
6
6
探究新知
租车费用与租车种类有关.设租用x辆甲种客车,则租车费用y(单位:元)是 x 的函数,即 :
y=400x+280(6-x)
化简为: y=120x+1680
(2)给出最节省费用的租车方案.
探究新知
在考虑上述问题的基础上,你能得出几种不同的租车方案?为节省费用应选择其中的哪种方案?试说明理由.
4两甲种客车,2两乙种客车;
5两甲种客车,1辆乙种客车;
y1=120×4+1680=2160
y2=120×5+1680=2280
应选择方案一,它比方案二节约120元.
方案一
方案二
探究新知
归
纳
解决含有多个变量的问题时,可以分析这些变量之间的关系,从中选取一个取值能影响其他变量的值的变量作为自变量.然后根据问题的条件寻求可以反映实际问题的函数,以此作为解决问题的数学模型.
归纳小结
选择方案的基本步骤
1.理解题意并建立函数模型;
2.利用不等式(组)或方程(组)确定自变量的取值范围或取值;
3.结合实际确定最佳方案.
归纳小结
1.某商店需要购进一批电视机和洗衣机,根据市场调查,决定电视机进货量不少于洗衣机进货量的一半.电视机与洗衣机的进价和售价如下表:
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}类别
电视机
洗衣机
进价(元/台)
1800
1500
售价(元/台)
2000
1600
计划购进电视机和洗衣机共100台,商店最多可筹集资金161800元.
课堂练习
(1)请你帮助商店算一算有多少种进货方案?(不考虑除进价之外的其他费用)
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}类别
电视机
洗衣机
进价(元/台)
1800
1500
售价(元/台)
2000
1600
解:设电视机进货x台,则洗衣机进货(100-x)台.
则由题意得:1800x+1500×(100-x)≤161800.
解得x≤39.
又∵x≥ (100-x),∴x≥34,∴34≤x≤39.
∴商店一共有6种进货方案.
课堂练习
(2)哪种进货方案待商店销售购进的电视机与洗衣机完毕后获得利润最多?并求出最多利润.(利润=售价-进价)
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}类别
电视机
洗衣机
进价(元/台)
1800
1500
售价(元/台)
2000
1600
课堂练习
设利润为y元,则由题意得:
y=(2000-1800)·x+(1600-1500)(100-x)
=100x+10000.
∵34≤x≤39,
∴当x=39时,ymax=100×39+10000=13900.
∴当商店购进电视机39台、洗衣机61台时,获得的利润最多,为13900元.
课堂练习
2. 某饮料厂为了开发新产品,现有A、B两种果汁原料各19千克、17.2千克,试制甲、乙两种新型饮料50千克,下表是实验的相关数据:
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}
甲
乙
A(单位:千克)
0.5
0.2
B(单位:千克)
0.3
0.4
类别
每千克含量
课堂练习
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}
甲
乙
A(单位:千克)
0.5
0.2
B(单位:千克)
0.3
0.4
(1)假设甲种饮料需配制x千克,请你写出满足题意的不等式组,并求出其解集;
类别
每千克含量
解:
解集为28≤x≤30.
0.5x+(50-x)×0.2≤19,
0.3x+(50-x) ×0.4≤17.2
课堂练习
(2)设甲种饮料每千克成本为4元,乙种饮料每千克成本为3元,这两种饮料的成本总额为y元,请写出y关于x的函数表达式.根据(1)的运算结果,确定当甲种饮料配制多少千克时,甲、乙两种饮料的成本总额最少?
y关于x的函数表达式为:y=4x+(50-x)×3=x+150.
∵28≤x≤30,∴当x=28时,ymin=28+150=178.
∴当甲种饮料配制28千克时,甲、乙两种饮料的成本总额最少,为178元.
课堂练习
3.康乐公司在A、B两地分别有同型号的机器17台和15台,现要运往甲地18台,乙地14台.从A、B两地运往甲、乙两地的费用如下表:
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}
甲地(元/台)
乙地(元/台)
A地
600
500
B地
400
800
目的地
出发地
课堂练习
解:如果从A地运往甲地x台,则从A地运往乙地(17-x)台,从B地运往甲地(18-x)台,从B地运往乙地(x-3)台.
则由题意得:y=600x+500×(17-x)+400×(18-x)+800×(x-3)=500x+13300.
(1)如果从A地运往甲地x台,求完成以上调运所需总费用y(元)关于x(台)的函数关系式;
课堂练习
∴完成以上调运所需总费用y(元)关于x(台)的函数关系式为y=500x+13300(3≤x≤17).
x≥0
x-3≥0
17-x≥0
18-x≥0
∵
解得3≤x≤17.
课堂练习
∵3≤x≤17,
∴当x=3时,ymin=500×3+13300=14800.
∴当从A地运3台机器到甲地,运14台到乙地,从B地运15台到甲地时,所需的总费用最少,为14800元.
(2)若康乐公司请你设计一种最佳调运方案,使总费用最少,则该公司完成以上调运方案至少需要多少费用?
课堂练习
选择方案的基本步骤
1.理解题意并建立函数模型;
2.利用不等式(组)或方程(组)确定自变量的取值范围或取值;
3.结合实际确定最佳方案.
课堂小结
https://www.21cnjy.com/help/help_extract.php
