第六章 圆周运动 单元练习Word版含答案
文档属性
| 名称 | 第六章 圆周运动 单元练习Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 773.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-27 20:58:42 | ||
图片预览



文档简介
第六章 圆周运动
一、选择题
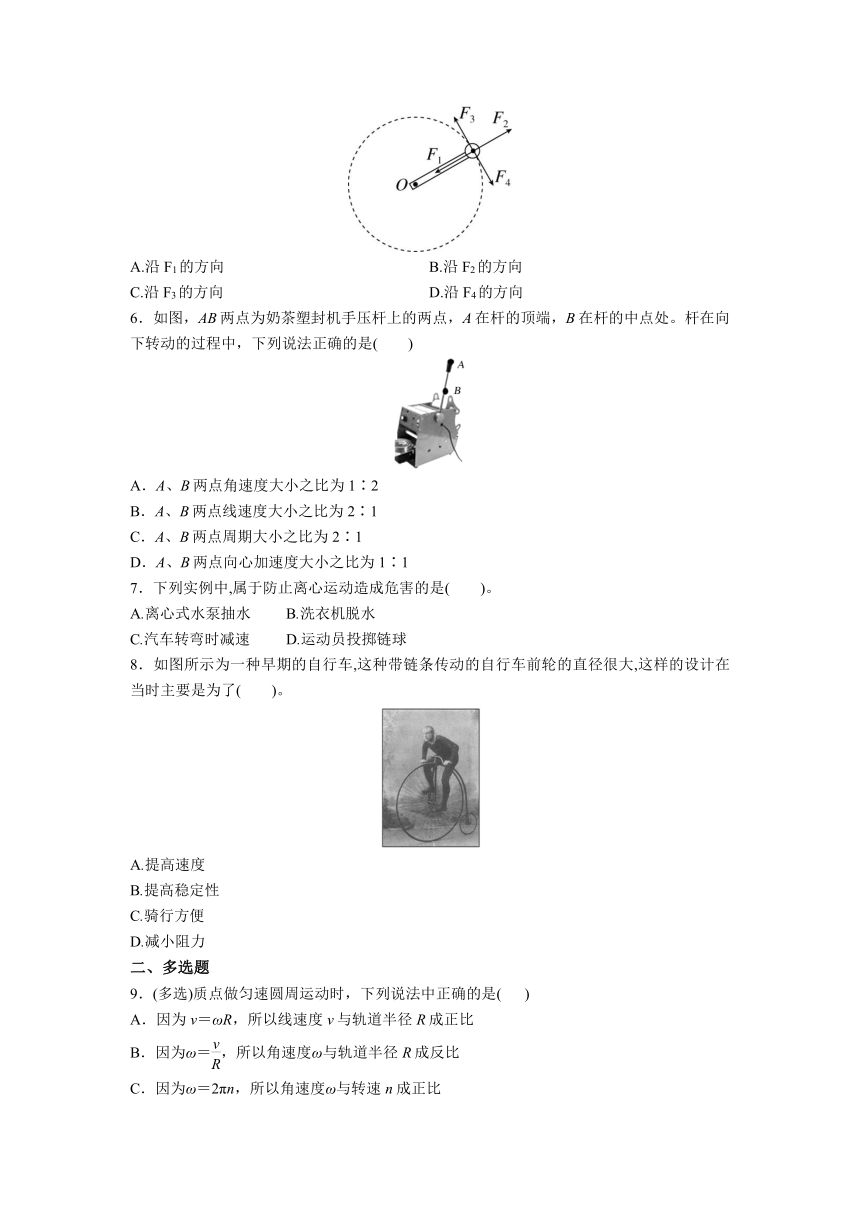
1.用一根细线一端系一可视为质点的小球,另一端固定在一光滑锥顶上,如图所示,设小球在水平面内做匀速圆周运动的角速度为ω,线的张力为T,则T随ω2变化的图像是( )
2.中国保护大熊猫研究中心之一的雅安碧峰峡基地位于东经103°,北纬30°.地球可以看作半径为R的球体,则在该中心处的物体与赤道上的物体随地球自转的向心加速度之比为( )
A.∶3 B.∶2
C.2∶ D.1∶2
3.如图所示,两轮用皮带传动,皮带不打滑.图中有A、B、C三点,这三点所在处半径rA>rB=rC,则这三点的向心加速度aA、aB、aC间的关系是( )
A.aA=aB=aC B.aC>aA>aB
C.aCaA
4.如图所示是自行车传动结构的示意图,其中Ⅰ是半径为r1的牙盘(大齿轮),Ⅱ是半径为r2的飞轮(小齿轮),Ⅲ是半径为r3的后轮,若自行车前进的速度为v,则牙盘的周期为( )
A. B.
D.v D.v
5.如图所示,一根轻杆(质量不计)的一端以O点为固定转轴,另一端固定一个小球,小球以O点为圆心在竖直平面内沿顺时针方向做匀速圆周运动.当小球运动到图中位置时,轻杆对小球作用力的方向可能( )
A.沿F1的方向 B.沿F2的方向
C.沿F3的方向 D.沿F4的方向
6.如图,AB两点为奶茶塑封机手压杆上的两点,A在杆的顶端,B在杆的中点处。杆在向下转动的过程中,下列说法正确的是( )
A.A、B两点角速度大小之比为1∶2
B.A、B两点线速度大小之比为2∶1
C.A、B两点周期大小之比为2∶1
D.A、B两点向心加速度大小之比为1∶1
7.下列实例中,属于防止离心运动造成危害的是( )。
A.离心式水泵抽水 B.洗衣机脱水
C.汽车转弯时减速 D.运动员投掷链球
8.如图所示为一种早期的自行车,这种带链条传动的自行车前轮的直径很大,这样的设计在当时主要是为了( )。
A.提高速度
B.提高稳定性
C.骑行方便
D.减小阻力
二、多选题
9.(多选)质点做匀速圆周运动时,下列说法中正确的是( )
A.因为v=ωR,所以线速度v与轨道半径R成正比
B.因为ω=,所以角速度ω与轨道半径R成反比
C.因为ω=2πn,所以角速度ω与转速n成正比
D.因为ω=,所以角速度ω与周期T成反比
10.(多选)公路急转弯处通常是交通事故多发地带.如图,某公路急转弯处是一圆弧,当汽车行驶的速率为vc时,汽车恰好没有向公路内外两侧滑动的趋势.则在该弯道处( )
A.路面外侧高内侧低
B.车速只要低于vc,车辆便会向内侧滑动
C.车速高于vc,只要不超出某一最高限度,车辆便不会向外侧滑动
D.当路面结冰时,与未结冰时相比,vc的值变小
11.(多选)如图所示,竖直平面内有一固定的圆形轨道,质量为m的小球在其内侧做圆周运动,在某圆周运动中,小球以速度v通过最高点时,恰好对轨道没有压力,经过轨道最低点时速度大小为2v,已知重力加速度为g,下列说法正确的是( )
A.圆形轨道半径为gv2
B.小球在轨道最高点的加速度大小为g
C.小球在轨道最低点受到轨道的支持力大小为4mg
D.小球在轨道最低点受到轨道的支持力大小为5mg
12.(多选)如图所示,两根长度不同的细线分别系有两个完全相同的小球,细线的上端都系于O点,设法让两个小球均在同一水平面上做匀速圆周运动,已知L1与竖直方向的夹角为60°、L2与竖直方向的夹角为30°,下列说法正确的是( )。
A.细线L1和细线L2所受的拉力大小之比为∶1
B.小球m1和m2的角速度大小之比为∶1
C.小球m1和m2的向心力大小之比为3∶1
D.小球m1和m2的线速度大小之比为3∶1
三、解答题
13.一物理兴趣小组利用学校实验室的数字实验系统“探究物体做圆周运动时向心力与角速度、半径的关系”.在保证重物的质量m和做圆周运动的角速度ω不变的情况下,改变重物做圆周运动的半径r,得到几组向心力F与半径r的数据,记录到表1中.
表1 向心力F与半径r的测量数据
次数 1 2 3 4 5
半径r/mm 50 60 70 80 90
向心力F/N 5.46 6.55 7.64 8.74 9.83
在保证重物的质量m和做圆周运动的半径r不变的情况下,改变重物做圆周运动的角速度ω,得到几组向心力F和角速度ω的数据,记录到表2中.
表2 向心力F与角速度ω的测量数据
次数 1 2 3 4 5
角速度 ω/(rad·s-1) 6.58 9.3 11.0 14.4 21.8
向心力F/N 0.098 3 0.226 6 0.282 1 0.458 3 1.080 7
(1)根据上面的测量结果,分别在图甲和图乙中作出F-r图线和F-ω图线.
(2)若作出的F-ω图线不是直线,可以尝试作F-ω2图线,试在图丙中作出F-ω2图线.
(3)通过以上实验探究可知,向心力与转动半径成________,与角速度的平方成________.
14.为验证向心力公式,某探究小组设计了如图所示的演示实验,在刻度尺的一端钻一个小孔,使小孔恰能穿过一根细线,线下端挂一质量为m,直径为d的小钢球。将刻度尺固定在水平桌面上,测量出悬点到钢球的细线长度为l,使钢球在水平面内做匀速圆周运动,圆心为O,待钢球的运动稳定后,用眼睛从刻度尺上方垂直于刻度尺往下看,读出钢球外侧到O点的距离r,并用秒表测量出钢球转动n圈用的时间t。则:
(1)小钢球做圆周运动的周期T= 。?
(2)小钢球做圆周运动的向心力Fn= (用m,n,r,d,t表示)。?
四、计算题
15.如图所示,置于圆形水平转台边缘的小物块随转台转动。缓慢地增大转台的转速,当转速达到某一数值时,物块恰好滑离转台开始做平抛运动。现测得转台半径r=0.5 m,离水平地面的高度h=0.8 m,物块平抛落地过程水平位移的大小s=0.4 m。设物块所受的最大静摩擦力等于滑动摩擦力,重力加速度g取10 m/s2。求:
(1)物块做平抛运动的初速度大小v0;
(2)物块与转台间的动摩擦因数μ。
16.厢式货车在水平路面上做弯道训练。圆弧形弯道的半径为R=8 m,车轮与路面间的动摩擦因数为μ=0.8,滑动摩擦力等于最大静摩擦力。货车顶部用细线悬挂一个小球P,在悬点O处装有拉力传感器。车沿平直路面做匀速运动时,传感器的示数为F0=4 N。(g取10 m/s2)
(1)该货车在此圆弧形弯道上做匀速圆周运动时,为了防止侧滑,车的最大速度vm是多大?
(2)该货车某次在此弯道上做匀速圆周运动,稳定后传感器的示数为F=5 N,此时细线与竖直方向的夹角θ是多大?此时货车的速度v是多大?
17.在我国南方山区有一种简易水轮机,如图所示,从悬崖上流出的水可看作连续做平抛运动的物体,水流轨迹与下边放置的轮子边沿相切,水冲击轮子边缘上安装的挡水板,可使轮子连续转动,输出动力。当该系统工作稳定时,可近似认为水的末速度与轮子边缘的线速度相同。设水的流出点比轮轴高h=5.6 m,轮子半径R=1 m。调整轮轴O的位置,使水流与轮边缘切点相对应的半径与水平线成37°。取g=10 m/s2,sin 37°=0.6,cos 37°=0.8。
(1)求水流的初速度v0的大小。
(2)若不计挡水板的大小,则轮子转动的角速度为多少?
参考答案
一、选择题
1.C
【解析】
设绳长为L,锥面与竖直方向夹角为θ,当ω=0时,小球静止,受重力mg、支持力N和绳的拉力T而平衡,T=mgcosθ≠0,所以A项、B项都不正确;ω增大时,T增大,N减小,当N=0时,角速度为ω0。当ω<ω0时,由牛顿第二定律得,Tsinθ-Ncosθ=mω2Lsinθ,Tcosθ+Nsinθ=mg,解得T=mω2Lsin2θ+mgcosθ;当ω>ω0时,小球离开锥面,绳与竖直方向夹角变大,设为β,由牛顿第二定律得Tsinβ=mω2Lsinβ,所以T=mLω2,可知T-ω2图线的斜率变大,所以C项正确,D错误。故选C。
2.B
【解析】
向心加速度a=rω2,在该中心处的物体与赤道上的物体随地球自转的角速度相同,所以加速度之比为轨道半径之比,即Rcos 30°∶R=∶2,B正确.
3.C
【解析】
A、B两点通过同一根皮带传动,线速度大小相等,即vA=vB,由于rA>rB,根据a=可知aArC,根据a=ω2r可知aC4.B
【解析】
由题意结合图形可知,飞轮和后轮具有相同的角速度,后轮的线速度大小为v,可得飞轮的角速度为ω=,飞轮和牙盘具有相同的线速度,可得二者的角速度之比为r1∶r2,所以牙盘的角速度为ω牙盘=,其周期T=,选项B正确。
5.C
【解析】
因为小球做匀速圆周运动,所以其所受各力的合力一定指向圆心,充当向心力,若受杆弹力为F1、F2、F4时与重力的合力均不可能沿杆指向圆心,只有杆的弹力为F3时合力才可能沿杆指向圆心,故C项正确.
6.B
【解析】
A、B两点属于同轴转动,则A、B角速度相等,由于rA=2rB,根据公式v=ωr可知,A、B两点线速度大小之比为2∶1,故A错误,B正确;由于A、B角速度相等,由公式T=可知,A、B两点周期大小之比为1∶1,故C错误;由于A、B角速度相等,由公式a=ω2r可知,A、B两点向心加速度大小之比为2∶1,故D错误。
7.C
【解析】
离心式水泵抽水时,水被泵带动起来做离心运动,属于应用离心现象;洗衣机脱水时就是应用了水的离心运动;汽车转弯时要限制速度,来减小汽车所需的向心力,防止离心运动;链球运动员通过快速旋转将链球甩出,也是应用了离心现象。本题选择防止离心运动,C项符合题意。
8.A
【解析】
在骑车人脚蹬车轮转速一定的情况下,据公式v=ωr知,轮子半径越大,车轮边缘的线速度越大,车行驶得也就越快,A项正确。
二、多选题
9.CD
【解析】
ω一定时,线速度v与轨道半径R成正比,选项A错误。v一定时,角速度ω与轨道半径R成反比,选项B错误。在用转速或周期表示角速度时,角速度与转速成正比,与周期成反比,选项C、D正确。
10.AC
解析: AC
汽车以速率vc转弯,需要指向内侧的向心力,汽车恰好没有向公路内外两侧滑动的趋势,说明此处公路内侧较低外侧较高,A正确.车速只要低于vc,车辆便有向内侧滑动的趋势,但不一定向内侧滑动,B错误.车速高于vc,由于车轮与地面间有摩擦力,只要不超出某一最高限度,车辆便不会向外侧滑动,C正确.根据题述,汽车以速率vc转弯,需要指向内侧的向心力,汽车恰好没有向公路内外两侧滑动的趋势,没有受到摩擦力,所以当路面结冰时,与未结冰时相比,转弯时vc的值不变,D错误.
11.BD
【解析】
小球恰好过最高点由重力提供向心力,根据牛顿第二定律可得:mg=m,解得:r=,故A错误;在最高点,根据牛顿第二定律:mg=ma,可得小球在轨道最高点时的加速度大小为:a=g,故B正确;小球在最低点,根据牛顿第二定律可得:FN-mg=m,联立以上各式可得:FN=5mg,故C错误,D正确。
12.AC
【解析】
对任一小球研究,设细线与竖直方向的夹角为θ,小球在竖直方向受力平衡,则有FTcos θ=mg,解得FT=,所以细线L1和细线L2所受的拉力大小之比==,A项正确;小球所受合力的大小为mgtan θ,根据牛顿第二定律得mgtan θ=mLω2sin θ,得ω=,两小球离O点的竖直距离Lcos θ相等,所以角速度相等,B项错误;小球所受合力提供向心力,F=mgtan θ,则小球m1和m2的向心力大小之比==3,C项正确;根据v=ωr,角速度相等,得小球m1和m2的线速度大小之比===3,D项错误。
三、解答题
13.(1)
(2)
(3)正比 正比
14.(1) (2)mr-
四、计算题
15.(1)物块做平抛运动,在竖直方向上有h=gt2
在水平方向上有s=v0t
解得v0=s=1 m/s。
(2)物块离开转台时,最大静摩擦力提供向心力,有
Ffm=m
Ffm=μmg
解得μ==0.2。
16.(1)车沿平直路面做匀速运动时,小球处于平衡状态,传感器的示数为F0=mg=4 N
得到m=0.4 kg
该货车在此圆弧形弯道上做匀速圆周运动时,地面对其摩擦力提供向心力,为了防止侧滑,向心力不能超过最大静摩擦力,即μmg≥
代入数据得:v≤=8 m/s,故vm=8 m/s。
(2)小球受力如图所示,重力mg=4 N,方向竖直向下,拉力F=5 N,二者的合力沿水平方向提供向心力,根据几何关系得到=3 N
代入数据得v= m/s=2 m/s<8 m/s
所以没有侧滑,运动半径不变tan θ=
得到θ=37°。
17.(1)流出的水做平抛运动,设在空中运动的时间为t,在竖直方向有h-Rsin θ=gt2
代入数据解得t=1 s
由合速度与分速度的关系有tan θ=
解得v0=7.5 m/s。
(2)设水与轮接触时的速度大小为v,则有v==12.5 m/s
设轮子转动的角速度为ω,由于水的末速度与轮子边缘的线速度相同,则有ω==12.5 rad/s。
一、选择题
1.用一根细线一端系一可视为质点的小球,另一端固定在一光滑锥顶上,如图所示,设小球在水平面内做匀速圆周运动的角速度为ω,线的张力为T,则T随ω2变化的图像是( )
2.中国保护大熊猫研究中心之一的雅安碧峰峡基地位于东经103°,北纬30°.地球可以看作半径为R的球体,则在该中心处的物体与赤道上的物体随地球自转的向心加速度之比为( )
A.∶3 B.∶2
C.2∶ D.1∶2
3.如图所示,两轮用皮带传动,皮带不打滑.图中有A、B、C三点,这三点所在处半径rA>rB=rC,则这三点的向心加速度aA、aB、aC间的关系是( )
A.aA=aB=aC B.aC>aA>aB
C.aC
4.如图所示是自行车传动结构的示意图,其中Ⅰ是半径为r1的牙盘(大齿轮),Ⅱ是半径为r2的飞轮(小齿轮),Ⅲ是半径为r3的后轮,若自行车前进的速度为v,则牙盘的周期为( )
A. B.
D.v D.v
5.如图所示,一根轻杆(质量不计)的一端以O点为固定转轴,另一端固定一个小球,小球以O点为圆心在竖直平面内沿顺时针方向做匀速圆周运动.当小球运动到图中位置时,轻杆对小球作用力的方向可能( )
A.沿F1的方向 B.沿F2的方向
C.沿F3的方向 D.沿F4的方向
6.如图,AB两点为奶茶塑封机手压杆上的两点,A在杆的顶端,B在杆的中点处。杆在向下转动的过程中,下列说法正确的是( )
A.A、B两点角速度大小之比为1∶2
B.A、B两点线速度大小之比为2∶1
C.A、B两点周期大小之比为2∶1
D.A、B两点向心加速度大小之比为1∶1
7.下列实例中,属于防止离心运动造成危害的是( )。
A.离心式水泵抽水 B.洗衣机脱水
C.汽车转弯时减速 D.运动员投掷链球
8.如图所示为一种早期的自行车,这种带链条传动的自行车前轮的直径很大,这样的设计在当时主要是为了( )。
A.提高速度
B.提高稳定性
C.骑行方便
D.减小阻力
二、多选题
9.(多选)质点做匀速圆周运动时,下列说法中正确的是( )
A.因为v=ωR,所以线速度v与轨道半径R成正比
B.因为ω=,所以角速度ω与轨道半径R成反比
C.因为ω=2πn,所以角速度ω与转速n成正比
D.因为ω=,所以角速度ω与周期T成反比
10.(多选)公路急转弯处通常是交通事故多发地带.如图,某公路急转弯处是一圆弧,当汽车行驶的速率为vc时,汽车恰好没有向公路内外两侧滑动的趋势.则在该弯道处( )
A.路面外侧高内侧低
B.车速只要低于vc,车辆便会向内侧滑动
C.车速高于vc,只要不超出某一最高限度,车辆便不会向外侧滑动
D.当路面结冰时,与未结冰时相比,vc的值变小
11.(多选)如图所示,竖直平面内有一固定的圆形轨道,质量为m的小球在其内侧做圆周运动,在某圆周运动中,小球以速度v通过最高点时,恰好对轨道没有压力,经过轨道最低点时速度大小为2v,已知重力加速度为g,下列说法正确的是( )
A.圆形轨道半径为gv2
B.小球在轨道最高点的加速度大小为g
C.小球在轨道最低点受到轨道的支持力大小为4mg
D.小球在轨道最低点受到轨道的支持力大小为5mg
12.(多选)如图所示,两根长度不同的细线分别系有两个完全相同的小球,细线的上端都系于O点,设法让两个小球均在同一水平面上做匀速圆周运动,已知L1与竖直方向的夹角为60°、L2与竖直方向的夹角为30°,下列说法正确的是( )。
A.细线L1和细线L2所受的拉力大小之比为∶1
B.小球m1和m2的角速度大小之比为∶1
C.小球m1和m2的向心力大小之比为3∶1
D.小球m1和m2的线速度大小之比为3∶1
三、解答题
13.一物理兴趣小组利用学校实验室的数字实验系统“探究物体做圆周运动时向心力与角速度、半径的关系”.在保证重物的质量m和做圆周运动的角速度ω不变的情况下,改变重物做圆周运动的半径r,得到几组向心力F与半径r的数据,记录到表1中.
表1 向心力F与半径r的测量数据
次数 1 2 3 4 5
半径r/mm 50 60 70 80 90
向心力F/N 5.46 6.55 7.64 8.74 9.83
在保证重物的质量m和做圆周运动的半径r不变的情况下,改变重物做圆周运动的角速度ω,得到几组向心力F和角速度ω的数据,记录到表2中.
表2 向心力F与角速度ω的测量数据
次数 1 2 3 4 5
角速度 ω/(rad·s-1) 6.58 9.3 11.0 14.4 21.8
向心力F/N 0.098 3 0.226 6 0.282 1 0.458 3 1.080 7
(1)根据上面的测量结果,分别在图甲和图乙中作出F-r图线和F-ω图线.
(2)若作出的F-ω图线不是直线,可以尝试作F-ω2图线,试在图丙中作出F-ω2图线.
(3)通过以上实验探究可知,向心力与转动半径成________,与角速度的平方成________.
14.为验证向心力公式,某探究小组设计了如图所示的演示实验,在刻度尺的一端钻一个小孔,使小孔恰能穿过一根细线,线下端挂一质量为m,直径为d的小钢球。将刻度尺固定在水平桌面上,测量出悬点到钢球的细线长度为l,使钢球在水平面内做匀速圆周运动,圆心为O,待钢球的运动稳定后,用眼睛从刻度尺上方垂直于刻度尺往下看,读出钢球外侧到O点的距离r,并用秒表测量出钢球转动n圈用的时间t。则:
(1)小钢球做圆周运动的周期T= 。?
(2)小钢球做圆周运动的向心力Fn= (用m,n,r,d,t表示)。?
四、计算题
15.如图所示,置于圆形水平转台边缘的小物块随转台转动。缓慢地增大转台的转速,当转速达到某一数值时,物块恰好滑离转台开始做平抛运动。现测得转台半径r=0.5 m,离水平地面的高度h=0.8 m,物块平抛落地过程水平位移的大小s=0.4 m。设物块所受的最大静摩擦力等于滑动摩擦力,重力加速度g取10 m/s2。求:
(1)物块做平抛运动的初速度大小v0;
(2)物块与转台间的动摩擦因数μ。
16.厢式货车在水平路面上做弯道训练。圆弧形弯道的半径为R=8 m,车轮与路面间的动摩擦因数为μ=0.8,滑动摩擦力等于最大静摩擦力。货车顶部用细线悬挂一个小球P,在悬点O处装有拉力传感器。车沿平直路面做匀速运动时,传感器的示数为F0=4 N。(g取10 m/s2)
(1)该货车在此圆弧形弯道上做匀速圆周运动时,为了防止侧滑,车的最大速度vm是多大?
(2)该货车某次在此弯道上做匀速圆周运动,稳定后传感器的示数为F=5 N,此时细线与竖直方向的夹角θ是多大?此时货车的速度v是多大?
17.在我国南方山区有一种简易水轮机,如图所示,从悬崖上流出的水可看作连续做平抛运动的物体,水流轨迹与下边放置的轮子边沿相切,水冲击轮子边缘上安装的挡水板,可使轮子连续转动,输出动力。当该系统工作稳定时,可近似认为水的末速度与轮子边缘的线速度相同。设水的流出点比轮轴高h=5.6 m,轮子半径R=1 m。调整轮轴O的位置,使水流与轮边缘切点相对应的半径与水平线成37°。取g=10 m/s2,sin 37°=0.6,cos 37°=0.8。
(1)求水流的初速度v0的大小。
(2)若不计挡水板的大小,则轮子转动的角速度为多少?
参考答案
一、选择题
1.C
【解析】
设绳长为L,锥面与竖直方向夹角为θ,当ω=0时,小球静止,受重力mg、支持力N和绳的拉力T而平衡,T=mgcosθ≠0,所以A项、B项都不正确;ω增大时,T增大,N减小,当N=0时,角速度为ω0。当ω<ω0时,由牛顿第二定律得,Tsinθ-Ncosθ=mω2Lsinθ,Tcosθ+Nsinθ=mg,解得T=mω2Lsin2θ+mgcosθ;当ω>ω0时,小球离开锥面,绳与竖直方向夹角变大,设为β,由牛顿第二定律得Tsinβ=mω2Lsinβ,所以T=mLω2,可知T-ω2图线的斜率变大,所以C项正确,D错误。故选C。
2.B
【解析】
向心加速度a=rω2,在该中心处的物体与赤道上的物体随地球自转的角速度相同,所以加速度之比为轨道半径之比,即Rcos 30°∶R=∶2,B正确.
3.C
【解析】
A、B两点通过同一根皮带传动,线速度大小相等,即vA=vB,由于rA>rB,根据a=可知aA
【解析】
由题意结合图形可知,飞轮和后轮具有相同的角速度,后轮的线速度大小为v,可得飞轮的角速度为ω=,飞轮和牙盘具有相同的线速度,可得二者的角速度之比为r1∶r2,所以牙盘的角速度为ω牙盘=,其周期T=,选项B正确。
5.C
【解析】
因为小球做匀速圆周运动,所以其所受各力的合力一定指向圆心,充当向心力,若受杆弹力为F1、F2、F4时与重力的合力均不可能沿杆指向圆心,只有杆的弹力为F3时合力才可能沿杆指向圆心,故C项正确.
6.B
【解析】
A、B两点属于同轴转动,则A、B角速度相等,由于rA=2rB,根据公式v=ωr可知,A、B两点线速度大小之比为2∶1,故A错误,B正确;由于A、B角速度相等,由公式T=可知,A、B两点周期大小之比为1∶1,故C错误;由于A、B角速度相等,由公式a=ω2r可知,A、B两点向心加速度大小之比为2∶1,故D错误。
7.C
【解析】
离心式水泵抽水时,水被泵带动起来做离心运动,属于应用离心现象;洗衣机脱水时就是应用了水的离心运动;汽车转弯时要限制速度,来减小汽车所需的向心力,防止离心运动;链球运动员通过快速旋转将链球甩出,也是应用了离心现象。本题选择防止离心运动,C项符合题意。
8.A
【解析】
在骑车人脚蹬车轮转速一定的情况下,据公式v=ωr知,轮子半径越大,车轮边缘的线速度越大,车行驶得也就越快,A项正确。
二、多选题
9.CD
【解析】
ω一定时,线速度v与轨道半径R成正比,选项A错误。v一定时,角速度ω与轨道半径R成反比,选项B错误。在用转速或周期表示角速度时,角速度与转速成正比,与周期成反比,选项C、D正确。
10.AC
解析: AC
汽车以速率vc转弯,需要指向内侧的向心力,汽车恰好没有向公路内外两侧滑动的趋势,说明此处公路内侧较低外侧较高,A正确.车速只要低于vc,车辆便有向内侧滑动的趋势,但不一定向内侧滑动,B错误.车速高于vc,由于车轮与地面间有摩擦力,只要不超出某一最高限度,车辆便不会向外侧滑动,C正确.根据题述,汽车以速率vc转弯,需要指向内侧的向心力,汽车恰好没有向公路内外两侧滑动的趋势,没有受到摩擦力,所以当路面结冰时,与未结冰时相比,转弯时vc的值不变,D错误.
11.BD
【解析】
小球恰好过最高点由重力提供向心力,根据牛顿第二定律可得:mg=m,解得:r=,故A错误;在最高点,根据牛顿第二定律:mg=ma,可得小球在轨道最高点时的加速度大小为:a=g,故B正确;小球在最低点,根据牛顿第二定律可得:FN-mg=m,联立以上各式可得:FN=5mg,故C错误,D正确。
12.AC
【解析】
对任一小球研究,设细线与竖直方向的夹角为θ,小球在竖直方向受力平衡,则有FTcos θ=mg,解得FT=,所以细线L1和细线L2所受的拉力大小之比==,A项正确;小球所受合力的大小为mgtan θ,根据牛顿第二定律得mgtan θ=mLω2sin θ,得ω=,两小球离O点的竖直距离Lcos θ相等,所以角速度相等,B项错误;小球所受合力提供向心力,F=mgtan θ,则小球m1和m2的向心力大小之比==3,C项正确;根据v=ωr,角速度相等,得小球m1和m2的线速度大小之比===3,D项错误。
三、解答题
13.(1)
(2)
(3)正比 正比
14.(1) (2)mr-
四、计算题
15.(1)物块做平抛运动,在竖直方向上有h=gt2
在水平方向上有s=v0t
解得v0=s=1 m/s。
(2)物块离开转台时,最大静摩擦力提供向心力,有
Ffm=m
Ffm=μmg
解得μ==0.2。
16.(1)车沿平直路面做匀速运动时,小球处于平衡状态,传感器的示数为F0=mg=4 N
得到m=0.4 kg
该货车在此圆弧形弯道上做匀速圆周运动时,地面对其摩擦力提供向心力,为了防止侧滑,向心力不能超过最大静摩擦力,即μmg≥
代入数据得:v≤=8 m/s,故vm=8 m/s。
(2)小球受力如图所示,重力mg=4 N,方向竖直向下,拉力F=5 N,二者的合力沿水平方向提供向心力,根据几何关系得到=3 N
代入数据得v= m/s=2 m/s<8 m/s
所以没有侧滑,运动半径不变tan θ=
得到θ=37°。
17.(1)流出的水做平抛运动,设在空中运动的时间为t,在竖直方向有h-Rsin θ=gt2
代入数据解得t=1 s
由合速度与分速度的关系有tan θ=
解得v0=7.5 m/s。
(2)设水与轮接触时的速度大小为v,则有v==12.5 m/s
设轮子转动的角速度为ω,由于水的末速度与轮子边缘的线速度相同,则有ω==12.5 rad/s。
