2020-2021学年北师大版七年级数学下册4.1认识三角形(三)(21张)
文档属性
| 名称 | 2020-2021学年北师大版七年级数学下册4.1认识三角形(三)(21张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-28 22:48:38 | ||
图片预览





文档简介
(共21张PPT)
认识三角形(三)
用铅笔可以支起一张均匀的三角形卡片,你知道怎样确定这个支撑点的位置吗?
感受三角形的重心
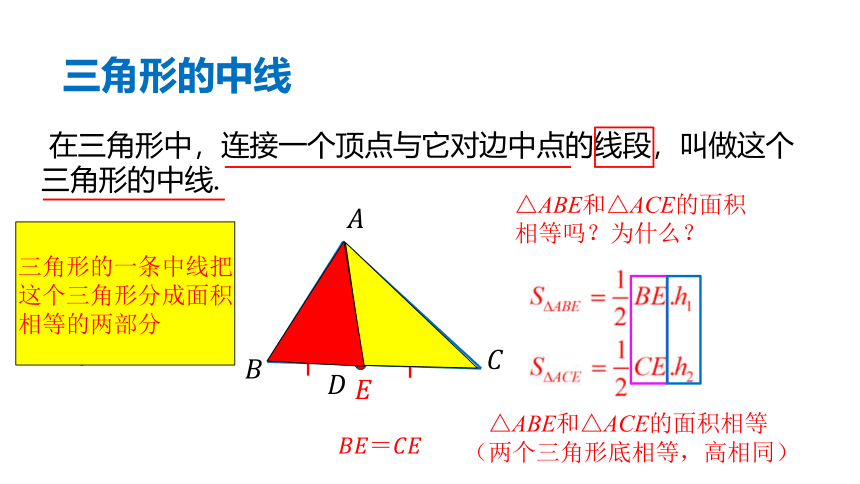
在三角形中,连接一个顶点与它对边中点的线段,叫做这个
三角形的中线.
三角形的中线
是△ABC的
边上的中线
△ABE和△ACE的面积
相等吗?为什么?
△ABE和△ACE的面积相等
(两个三角形底相等,高相同)
三角形的一条中线把这个三角形分成面积相等的两部分
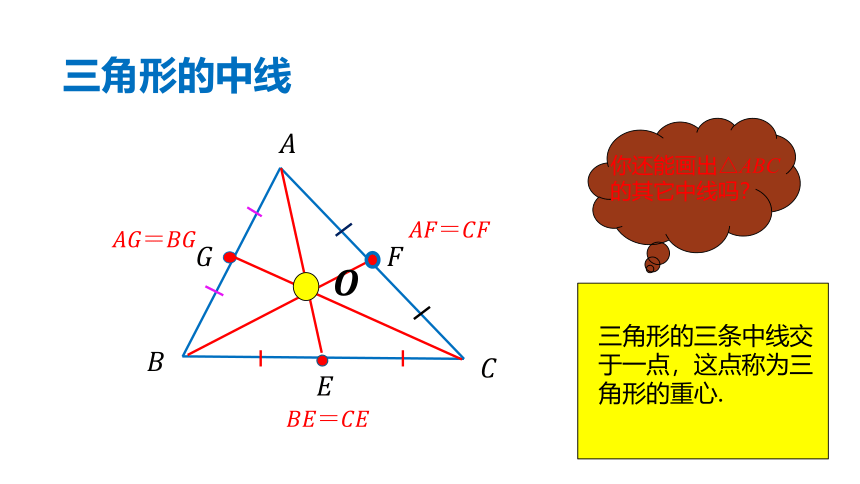
三角形的中线
你还能画出△ABC
的其它中线吗?
三条中线会交于
一点吗?
三条中线交于一点
三角形的三条中线交于一点,这点称为三角形的重心.
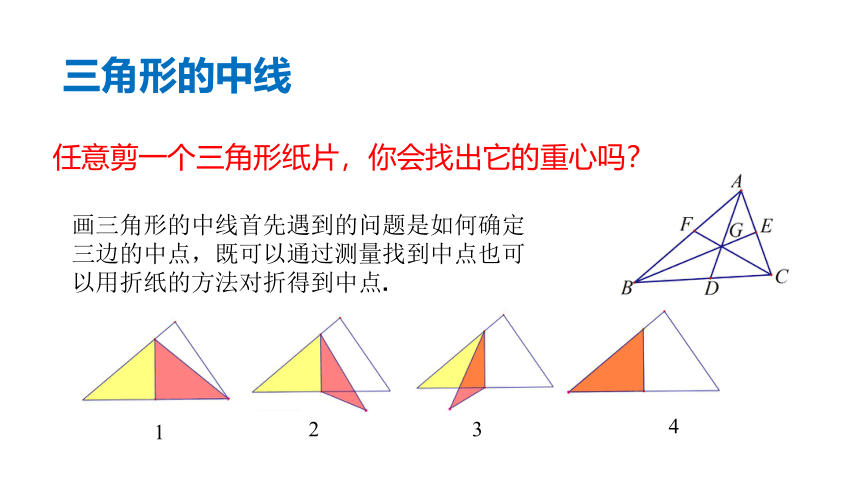
三角形的中线
画三角形的中线首先遇到的问题是如何确定三边的中点,既可以通过测量找到中点也可以用折纸的方法对折得到中点.
1
2
3
4
任意剪一个三角形纸片,你会找出它的重心吗?
三角形的中线
用铅笔可以支起一张均匀的三角形卡片,你知道怎样确定这个支撑点的位置吗?
三角形的中线
练习1:
已知AD是△ABC的中线,那=_________=_______
若△ABC的面积是16,则△ADC的面积是__________.
知中线
得中点
解:
三角形的中线
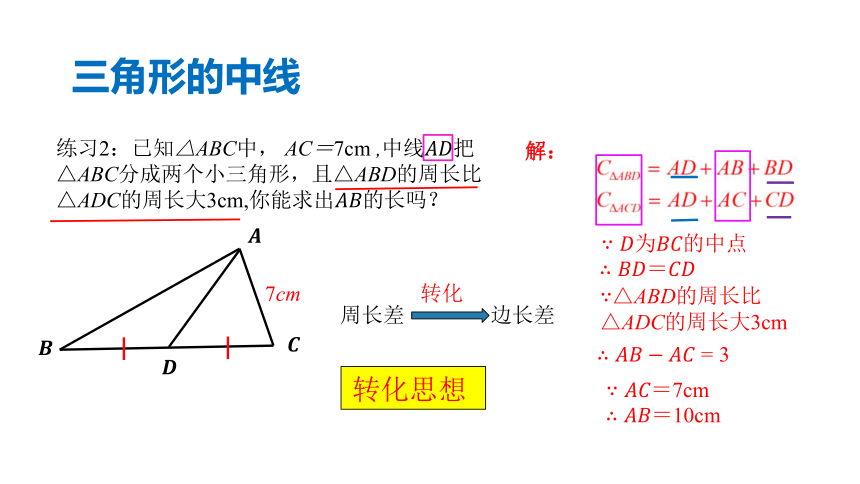
练习2:已知△ABC中,
AC=7cm
,中线把
△ABC分成两个小三角形,且△ABD的周长比
△ADC的周长大3cm,你能求出的长吗?
7cm
转化思想
△ABD的周长比
△ADC的周长大3cm
周长差
边长差
转化
三角形的中线
变式
已知△中,=7cm,中线把△分成两个小三角形
这两个小三角形的周长的差
是3cm,你能求出的长吗?
分类讨论
解:
解:
三角形的中线
1.5
练习3:如图,在△ABC中D
,E分别是BC,AD的中点,
那么
cm2
数形结合
2
1
三角形的角平分线
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.
∠1=∠2
三角形的角平分线与角平分线一样吗?
注意:三角形的角平分线是线段,而角平分
线则是射线,这是二者的重要区别.
2
三角形的角平分线
如果现在你手上有一张三角形的薄纸,你能想出几种办法来画出它的一个内角的平分线呢?
三角形的三条角平分线,同学们可以利用量角器画出,也可以使用圆规画出,还可以利用折纸的方法得到
想一想
三角形的角平分线
同前面探索三角形的三条中线交于一点一样,三角形的三条角平分线交于一点的结论也是通过画图折纸直观感知确认,同学们可以自行选择不同形状的三角形进行验证.
在每个三角形中,这三条角平分线之间有怎样的位置关系?
三角形的角平分线
三角形的三条角平分线交于一点
(这一点叫做三角形的内心)
三角形的角平分线
55
55
练习1:
如图,在△ABC中,
AD是∠BAC的平分线,已知∠B=30°,∠C=
40
°
则∠BAD=
°,
∠CAD=
°.
角平分线
相等的角
三角形的角平分线
1
2
解:
三角形的角平分线
变式训练:
如图,在△ABC中,
∠
ABC=
∠
C,BD是∠
ABC的平分线,
∠
BDC=102°
求∠
A的度数.
解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
设∠ABD=∠CBD=x°
∴∠ABC=2x°
∵∠ABC=∠C
∴∠C=2x°
∵∠BDC=102°
∴∠ABC=
2x°=52°
∴∠C=∠ABC=
52°
∴x+2x+
102
=180
∴x=26
∴∠A=180°-52°-52°=76°
方程思想
当堂检测题
如图1,若AD是△ABC的角平分线(D在BC所在直线上),那么∠
BAD=
∠
.
如图2若
AD是△ABC的中线,已知AB=5cm,AC=3cm,则△ABD与△ACD的周长之差是
.
3.
如图3,在△ABC中,
∠
BAC=60°,
∠
B=45°
AD是△ABC的一条角平分线,求∠
ADB的度数.
?
CAD
2cm
解:∵AD是∠BAC的平分线
∴
∠
DAB=
∠
BAC
=
×60°=30°
∴
∠
ADB=180°-45°-30°=105°
1
2
3
课后思考题
2
1
归纳总结
三角形的三条中线交于一点(重心)
三角形的三条角平分线交于一点(内心)
归纳总结
数学思想方法
转化
方程
分类讨论
数形结合
长风破浪会有时,直挂云帆济沧海
加油吧,少年
认识三角形(三)
用铅笔可以支起一张均匀的三角形卡片,你知道怎样确定这个支撑点的位置吗?
感受三角形的重心
在三角形中,连接一个顶点与它对边中点的线段,叫做这个
三角形的中线.
三角形的中线
是△ABC的
边上的中线
△ABE和△ACE的面积
相等吗?为什么?
△ABE和△ACE的面积相等
(两个三角形底相等,高相同)
三角形的一条中线把这个三角形分成面积相等的两部分
三角形的中线
你还能画出△ABC
的其它中线吗?
三条中线会交于
一点吗?
三条中线交于一点
三角形的三条中线交于一点,这点称为三角形的重心.
三角形的中线
画三角形的中线首先遇到的问题是如何确定三边的中点,既可以通过测量找到中点也可以用折纸的方法对折得到中点.
1
2
3
4
任意剪一个三角形纸片,你会找出它的重心吗?
三角形的中线
用铅笔可以支起一张均匀的三角形卡片,你知道怎样确定这个支撑点的位置吗?
三角形的中线
练习1:
已知AD是△ABC的中线,那=_________=_______
若△ABC的面积是16,则△ADC的面积是__________.
知中线
得中点
解:
三角形的中线
练习2:已知△ABC中,
AC=7cm
,中线把
△ABC分成两个小三角形,且△ABD的周长比
△ADC的周长大3cm,你能求出的长吗?
7cm
转化思想
△ABD的周长比
△ADC的周长大3cm
周长差
边长差
转化
三角形的中线
变式
已知△中,=7cm,中线把△分成两个小三角形
这两个小三角形的周长的差
是3cm,你能求出的长吗?
分类讨论
解:
解:
三角形的中线
1.5
练习3:如图,在△ABC中D
,E分别是BC,AD的中点,
那么
cm2
数形结合
2
1
三角形的角平分线
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.
∠1=∠2
三角形的角平分线与角平分线一样吗?
注意:三角形的角平分线是线段,而角平分
线则是射线,这是二者的重要区别.
2
三角形的角平分线
如果现在你手上有一张三角形的薄纸,你能想出几种办法来画出它的一个内角的平分线呢?
三角形的三条角平分线,同学们可以利用量角器画出,也可以使用圆规画出,还可以利用折纸的方法得到
想一想
三角形的角平分线
同前面探索三角形的三条中线交于一点一样,三角形的三条角平分线交于一点的结论也是通过画图折纸直观感知确认,同学们可以自行选择不同形状的三角形进行验证.
在每个三角形中,这三条角平分线之间有怎样的位置关系?
三角形的角平分线
三角形的三条角平分线交于一点
(这一点叫做三角形的内心)
三角形的角平分线
55
55
练习1:
如图,在△ABC中,
AD是∠BAC的平分线,已知∠B=30°,∠C=
40
°
则∠BAD=
°,
∠CAD=
°.
角平分线
相等的角
三角形的角平分线
1
2
解:
三角形的角平分线
变式训练:
如图,在△ABC中,
∠
ABC=
∠
C,BD是∠
ABC的平分线,
∠
BDC=102°
求∠
A的度数.
解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
设∠ABD=∠CBD=x°
∴∠ABC=2x°
∵∠ABC=∠C
∴∠C=2x°
∵∠BDC=102°
∴∠ABC=
2x°=52°
∴∠C=∠ABC=
52°
∴x+2x+
102
=180
∴x=26
∴∠A=180°-52°-52°=76°
方程思想
当堂检测题
如图1,若AD是△ABC的角平分线(D在BC所在直线上),那么∠
BAD=
∠
.
如图2若
AD是△ABC的中线,已知AB=5cm,AC=3cm,则△ABD与△ACD的周长之差是
.
3.
如图3,在△ABC中,
∠
BAC=60°,
∠
B=45°
AD是△ABC的一条角平分线,求∠
ADB的度数.
?
CAD
2cm
解:∵AD是∠BAC的平分线
∴
∠
DAB=
∠
BAC
=
×60°=30°
∴
∠
ADB=180°-45°-30°=105°
1
2
3
课后思考题
2
1
归纳总结
三角形的三条中线交于一点(重心)
三角形的三条角平分线交于一点(内心)
归纳总结
数学思想方法
转化
方程
分类讨论
数形结合
长风破浪会有时,直挂云帆济沧海
加油吧,少年
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
