2020-2021学年沪科版数学七年级下册 第7章 一元一次不等式与不等式组 单元复习练习题(Word版 含答案)
文档属性
| 名称 | 2020-2021学年沪科版数学七年级下册 第7章 一元一次不等式与不等式组 单元复习练习题(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 89.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-28 00:00:00 | ||
图片预览


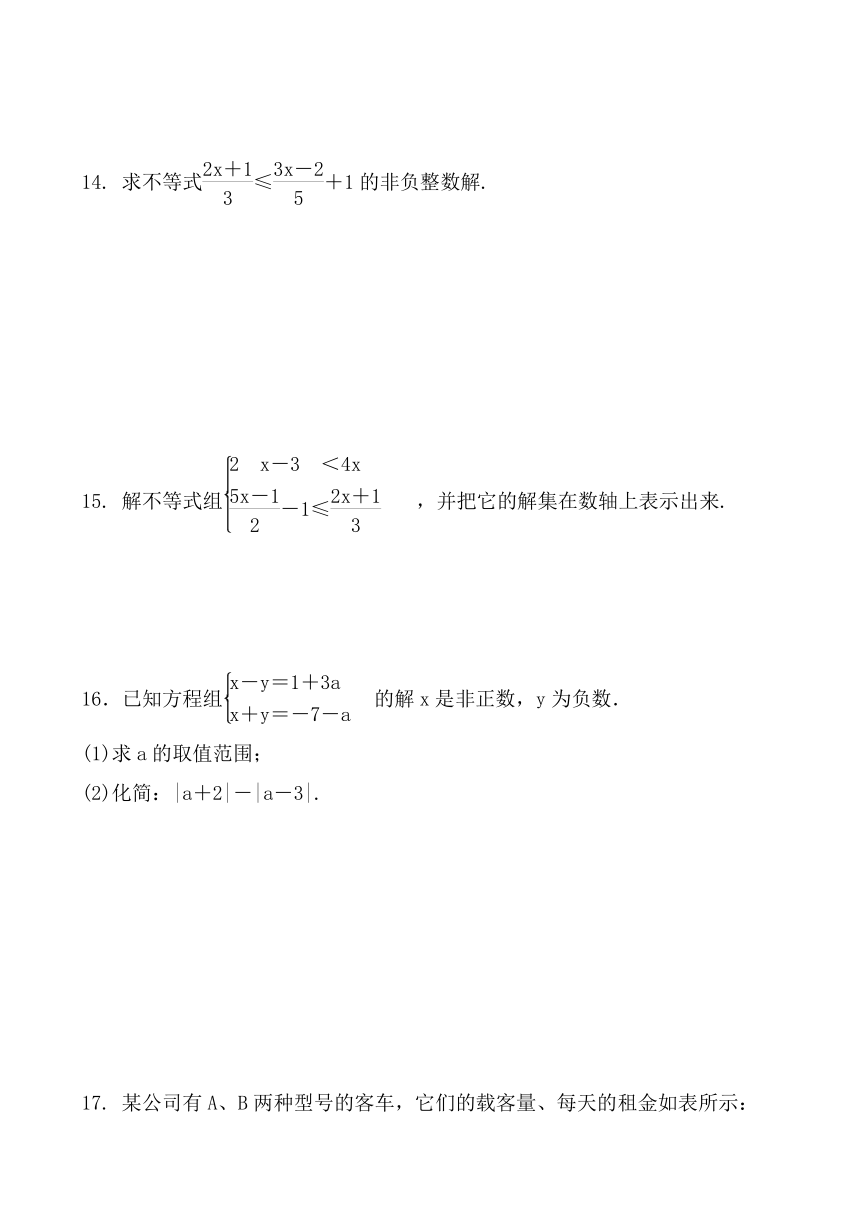
文档简介
第7章 一元一次不等式与不等式组
1.已知四个实数a、b、c、d,若a>b,c>d,则( )
A.a+c>b+d B.a-c>b-d
C.ac>bd
D.>
2.不等式x-1≤2的非负整数解有( )
A.1个 B.2个 C.3个 D.4个
3.不等式组的解集在数轴上表示正确的是( )
4.不等式组的整数解是( )
A.0
B.-1
C.-2
D.1
5.若不等式组无解,则实数a的取值范围是( )
A.a≥-1
B.a<-1
C.a≤1
D.a≤-1
6.若关于x的不等式组有解,则在其解集中,整数的个数不可能是( )
A.1
B.2
C.3
D.4
7.红星商店计划用不超过4200元的资金,购进甲、乙两种单价分别为60元、100元的商品共50件,据市场行情,销售甲、乙商品各一件分别可获利10元、20元,两种商品均售完.若所获利润大于750元,则该店进货方案有( )
A.3种
B.4种
C.5种
D.6种
8.
下列不等式的变形中,不正确的是(
)
A.若a>b,由a+1>b+1
B.若-a>-b,则a<b
C.若-x<y,则x>-3y
D.若-3x>a,则x>-a
9.已知关于x的不等式3x+mx>-5的解集如图所示,则m的值为
.
10.关于x的不等式组的解集为x<3,那么m的取值范围为
.
11.若关于x的不等式组有且只有两个整数解,则m的取值范围是
.
12.解不等式≤-1,并把解集在数轴上表示出来.
13.
解不等式组,并写出它的所有负整数解.
14.
求不等式≤+1的非负整数解.
15.
解不等式组,并把它的解集在数轴上表示出来.
16.已知方程组的解x是非正数,y为负数.
(1)求a的取值范围;
(2)化简:|a+2|-|a-3|.
17.
某公司有A、B两种型号的客车,它们的载客量、每天的租金如表所示:
A型号客车
B型号客车
载客量(人/辆)
30
45
租金(元/辆)
450
600
已知某中学计划租用两种型号的客车共10辆送七年级师生去某地参加社会实践活动,已知该中学租车的总费用不超过5600元.
(1)求最多能租用多少辆B型号客车?
(2)若七年级师生共有380人,请写出所有可能的租车方案.
18.某校开展校园艺术节系列活动,派小明到文体超市购买若干个文具袋作为奖品.这种文具袋标价每个10元,请认真阅读结账时老板与小明的对话:
(1)结合两人的对话内容,求小明原计划购买文具袋多少个?
(2)学校决定,再次购买钢笔和签字笔共50支作为补充奖品,两次购买奖品总支出不超过400元.其中钢笔标价每支8元,签字笔标价每支6元,经过沟通,这次老板给予8折优惠,那么小明最多可购买钢笔多少支?
答案:
1-8
ADBBD
CCD
9.
-
10.
m≥3
11.
-2≤m<1
12.
解:解集为x≥2,图略
13.
解:不等式组的解集为-3≤x<2.所以不等式组的所有负整数解为-3、-2、-1.
14.
解:
5(2x+1)≤3(3x-2)+15,10x+5≤9x-6+15,10x-9x≤-6+15-5,x≤4,则不等式的非负整数解为0、1、2、3、4
15.
解:
解2(x-3)<4x得x>-3,解-1≤得x≤1,则不等式组的解集为-3<x≤1,将不等式组的解集表示在数轴上如下:
16.
解:(1)解方程组得,由题意知x≤0,y<0,得,即,所以-2<a≤3;
(2)因为-2<a≤3,所以a+2>0,a-3≤0,|a+2|-|a-3|=a+2+(a-3)=a+2-3+a=2a-1.
17.
解:(1)设租用B型号的客车x辆,则租用A型号的客车(10-x)辆,依题意,得450(10-x)+600x≤5600,解得x≤7.又∵x为整数,∴x的最大值为7.答:最多能租用B型号客车7辆;
(2)设租用B型号的客车x辆,则租用A型号的客车(10-x)辆,依题意,得30(10-x)+45x≥380,解得x≥5.由(1)知,x≤7,∴5≤x≤7,∵x为整数,∴x为6或7.∴共有两种租车方案,方案一:租用A型号客车4辆、租用B型号客车6辆;方案二:租用A型号客车3辆、租用B型号客车7辆.
18.
解:(1)设小明原计划购买文具袋x个,则实际购买了(x+1)个,依题意,得10(x+1)×0.85=10x-17.解得x=17.答:小明原计划购买文具袋17个;
(2)设小明可购买钢笔y支,则购买签字笔(50-x)支,依题意,得[8y+6(50-y)]×80%≤400-10×17+17.解得y≤4.375,即y最大值=4.答:小明最多可购买钢笔4支.
1.已知四个实数a、b、c、d,若a>b,c>d,则( )
A.a+c>b+d B.a-c>b-d
C.ac>bd
D.>
2.不等式x-1≤2的非负整数解有( )
A.1个 B.2个 C.3个 D.4个
3.不等式组的解集在数轴上表示正确的是( )
4.不等式组的整数解是( )
A.0
B.-1
C.-2
D.1
5.若不等式组无解,则实数a的取值范围是( )
A.a≥-1
B.a<-1
C.a≤1
D.a≤-1
6.若关于x的不等式组有解,则在其解集中,整数的个数不可能是( )
A.1
B.2
C.3
D.4
7.红星商店计划用不超过4200元的资金,购进甲、乙两种单价分别为60元、100元的商品共50件,据市场行情,销售甲、乙商品各一件分别可获利10元、20元,两种商品均售完.若所获利润大于750元,则该店进货方案有( )
A.3种
B.4种
C.5种
D.6种
8.
下列不等式的变形中,不正确的是(
)
A.若a>b,由a+1>b+1
B.若-a>-b,则a<b
C.若-x<y,则x>-3y
D.若-3x>a,则x>-a
9.已知关于x的不等式3x+mx>-5的解集如图所示,则m的值为
.
10.关于x的不等式组的解集为x<3,那么m的取值范围为
.
11.若关于x的不等式组有且只有两个整数解,则m的取值范围是
.
12.解不等式≤-1,并把解集在数轴上表示出来.
13.
解不等式组,并写出它的所有负整数解.
14.
求不等式≤+1的非负整数解.
15.
解不等式组,并把它的解集在数轴上表示出来.
16.已知方程组的解x是非正数,y为负数.
(1)求a的取值范围;
(2)化简:|a+2|-|a-3|.
17.
某公司有A、B两种型号的客车,它们的载客量、每天的租金如表所示:
A型号客车
B型号客车
载客量(人/辆)
30
45
租金(元/辆)
450
600
已知某中学计划租用两种型号的客车共10辆送七年级师生去某地参加社会实践活动,已知该中学租车的总费用不超过5600元.
(1)求最多能租用多少辆B型号客车?
(2)若七年级师生共有380人,请写出所有可能的租车方案.
18.某校开展校园艺术节系列活动,派小明到文体超市购买若干个文具袋作为奖品.这种文具袋标价每个10元,请认真阅读结账时老板与小明的对话:
(1)结合两人的对话内容,求小明原计划购买文具袋多少个?
(2)学校决定,再次购买钢笔和签字笔共50支作为补充奖品,两次购买奖品总支出不超过400元.其中钢笔标价每支8元,签字笔标价每支6元,经过沟通,这次老板给予8折优惠,那么小明最多可购买钢笔多少支?
答案:
1-8
ADBBD
CCD
9.
-
10.
m≥3
11.
-2≤m<1
12.
解:解集为x≥2,图略
13.
解:不等式组的解集为-3≤x<2.所以不等式组的所有负整数解为-3、-2、-1.
14.
解:
5(2x+1)≤3(3x-2)+15,10x+5≤9x-6+15,10x-9x≤-6+15-5,x≤4,则不等式的非负整数解为0、1、2、3、4
15.
解:
解2(x-3)<4x得x>-3,解-1≤得x≤1,则不等式组的解集为-3<x≤1,将不等式组的解集表示在数轴上如下:
16.
解:(1)解方程组得,由题意知x≤0,y<0,得,即,所以-2<a≤3;
(2)因为-2<a≤3,所以a+2>0,a-3≤0,|a+2|-|a-3|=a+2+(a-3)=a+2-3+a=2a-1.
17.
解:(1)设租用B型号的客车x辆,则租用A型号的客车(10-x)辆,依题意,得450(10-x)+600x≤5600,解得x≤7.又∵x为整数,∴x的最大值为7.答:最多能租用B型号客车7辆;
(2)设租用B型号的客车x辆,则租用A型号的客车(10-x)辆,依题意,得30(10-x)+45x≥380,解得x≥5.由(1)知,x≤7,∴5≤x≤7,∵x为整数,∴x为6或7.∴共有两种租车方案,方案一:租用A型号客车4辆、租用B型号客车6辆;方案二:租用A型号客车3辆、租用B型号客车7辆.
18.
解:(1)设小明原计划购买文具袋x个,则实际购买了(x+1)个,依题意,得10(x+1)×0.85=10x-17.解得x=17.答:小明原计划购买文具袋17个;
(2)设小明可购买钢笔y支,则购买签字笔(50-x)支,依题意,得[8y+6(50-y)]×80%≤400-10×17+17.解得y≤4.375,即y最大值=4.答:小明最多可购买钢笔4支.
