2020-2021学年北师大版九年级数学下册第三章 圆 单元复习同步练习题(word版含答案)
文档属性
| 名称 | 2020-2021学年北师大版九年级数学下册第三章 圆 单元复习同步练习题(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 372.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-28 00:00:00 | ||
图片预览


文档简介
2020-2021学年北师大版九年级数学下册第三章
圆
单元复习同步练习题
一、选择题
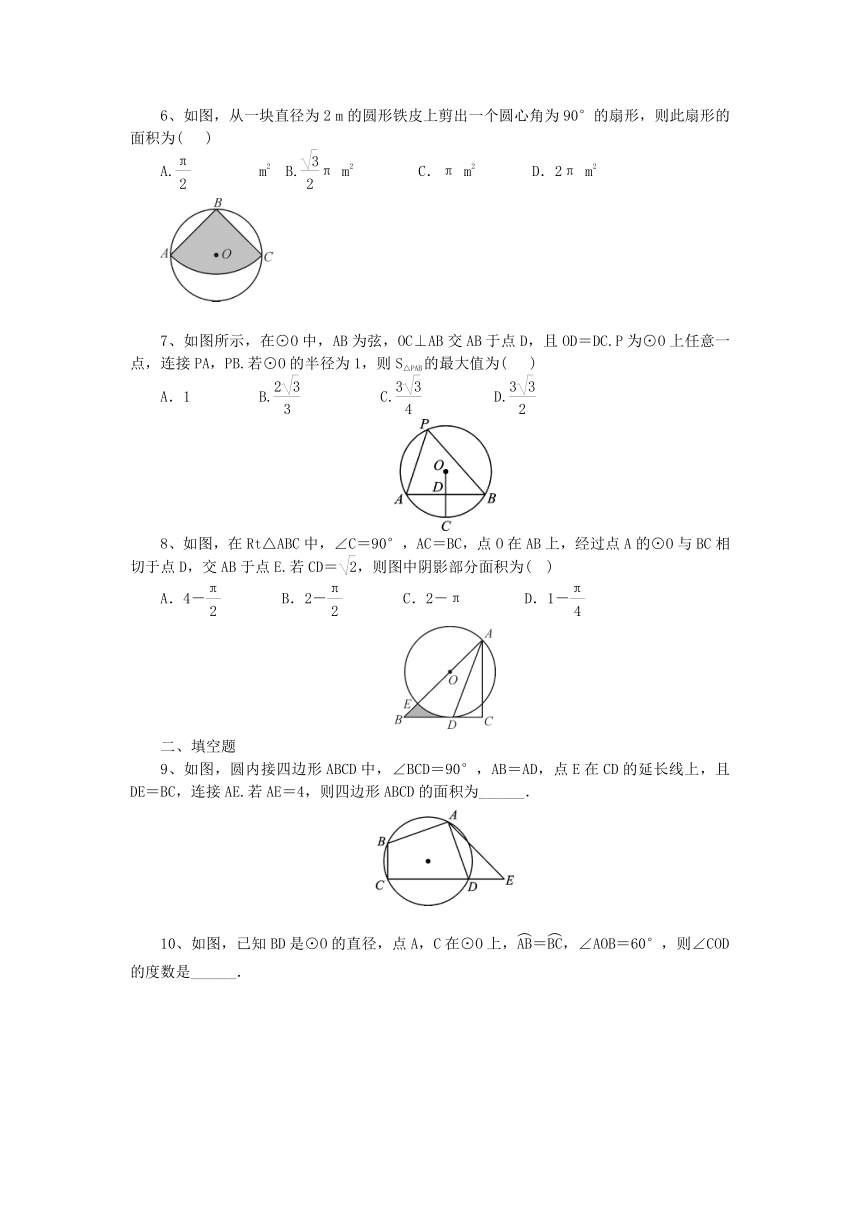
1、如图,AB,CD是⊙O的直径,=.若∠AOE=32°,则∠COE的度数是(
)
A.32°
B.60°
C.68°
D.64°
2、如图,AB是⊙O的直径,∠BOD=120°,点C为的中点,AC交OD于点E,DE=1,则AE的长为(
)
A.
B.
C.2
D.2
3、如图,A,B,C,D是⊙O上的四个点,AB=AC,AD交BC于点E,AE=3,ED=4,则AC的长为(
)
A.3
B.2
C.
D.3
4、一根水平放置的圆柱形输水管的横截面如图所示,其中有水部分水面宽8米,最深处水深2米,则此输水管道的半径是(
)
A.8米
B.6米
C.5米
D.4米
5、如图,已知⊙O是正方形ABCD的外接圆,点E是上任意一点,则∠ABE+∠ECD的度数为(
)
A.30°
B.45°
C.60°
D.90°
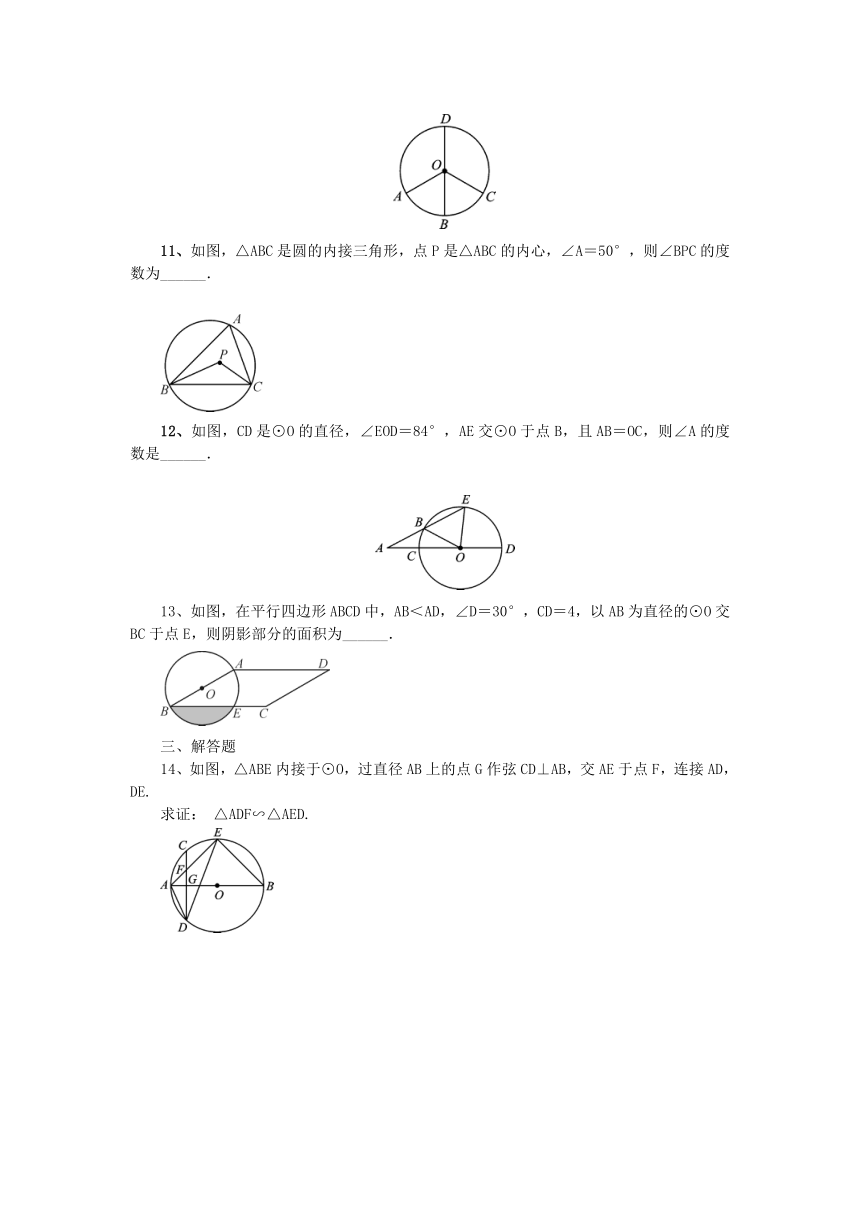
6、如图,从一块直径为2
m的圆形铁皮上剪出一个圆心角为90°的扇形,则此扇形的面积为(
)
A.
m2
B.π
m2
C.π
m2
D.2π
m2
7、如图所示,在⊙O中,AB为弦,OC⊥AB交AB于点D,且OD=DC.P为⊙O上任意一点,连接PA,PB.若⊙O的半径为1,则S△PAB的最大值为(
)
A.1
B.
C.
D.
8、如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.若CD=,则图中阴影部分面积为(
)
A.4-
B.2-
C.2-π
D.1-
二、填空题
9、如图,圆内接四边形ABCD中,∠BCD=90°,AB=AD,点E在CD的延长线上,且DE=BC,连接AE.若AE=4,则四边形ABCD的面积为______.
10、如图,已知BD是⊙O的直径,点A,C在⊙O上,=,∠AOB=60°,则∠COD的度数是______.
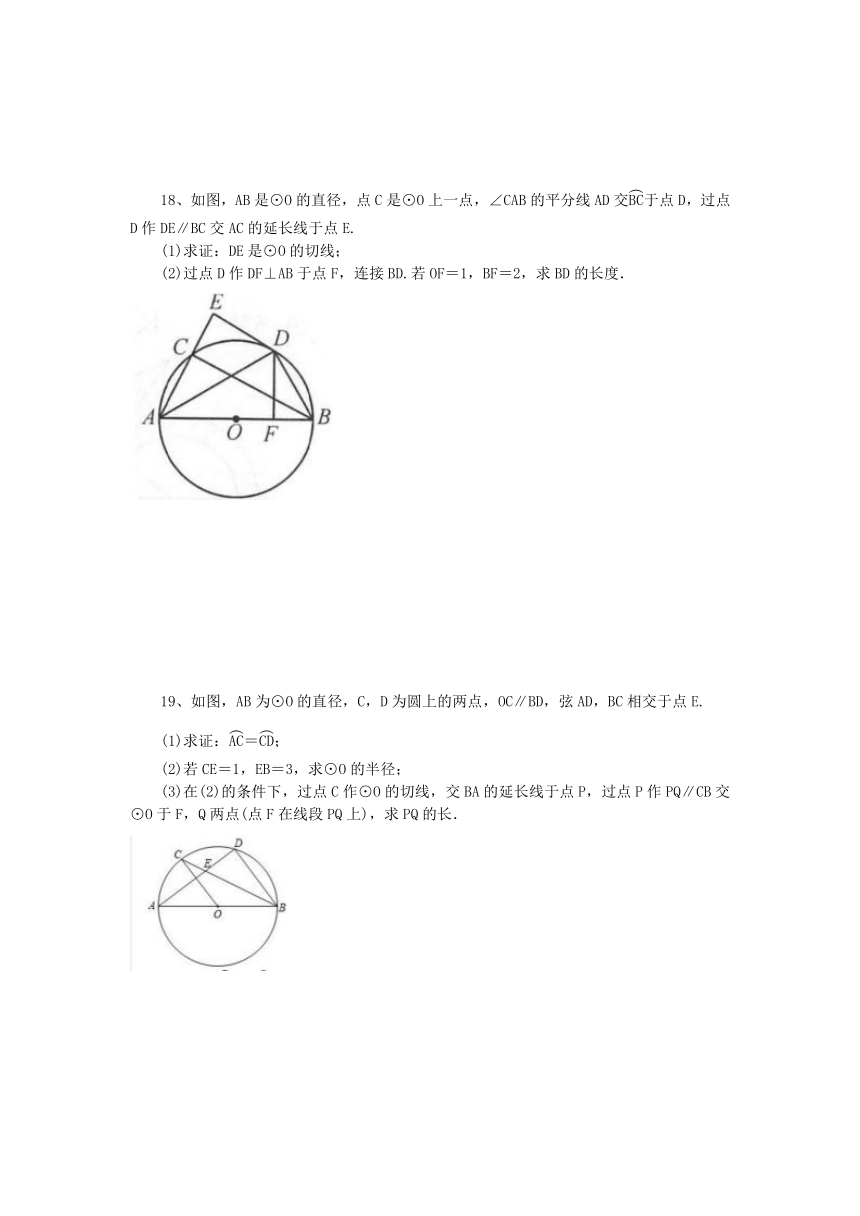
11、如图,△ABC是圆的内接三角形,点P是△ABC的内心,∠A=50°,则∠BPC的度数为______.
12、如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,则∠A的度数是______.
13、如图,在平行四边形ABCD中,AB<AD,∠D=30°,CD=4,以AB为直径的⊙O交BC于点E,则阴影部分的面积为______.
三、解答题
14、如图,△ABE内接于⊙O,过直径AB上的点G作弦CD⊥AB,交AE于点F,连接AD,DE.
求证:
△ADF∽△AED.
15、如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD,CD.过点D作⊙O的切线交AC的延长线于点P.求证:△ABD∽△DCP.
16、如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接BD,BE.
(1)求证:△ABD∽△AEB;
(2)当=时,求tanE.
17、如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC,AB的延长线于点E,F.
(1)求证:EF是⊙O的切线;
(2)若AC=4,CE=2,求的长度.(结果保留π)
18、如图,AB是⊙O的直径,点C是⊙O上一点,∠CAB的平分线AD交于点D,过点D作DE∥BC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)过点D作DF⊥AB于点F,连接BD.若OF=1,BF=2,求BD的长度.
19、如图,AB为⊙O的直径,C,D为圆上的两点,OC∥BD,弦AD,BC相交于点E.
(1)求证:=;
(2)若CE=1,EB=3,求⊙O的半径;
(3)在(2)的条件下,过点C作⊙O的切线,交BA的延长线于点P,过点P作PQ∥CB交⊙O于F,Q两点(点F在线段PQ上),求PQ的长.
20、如图,AB为⊙O直径,C,D是⊙O上的点,连接CB并延长与AD所在直线交于点F,EF⊥AB,垂足为E,连接CE,且CE=EF.
(1)证明:CE与⊙O相切;
(2)若AE=8,tan∠BCE=,求AD的长度.
21、如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)求证:CG=BG;
(3)若∠DBA=30°,CG=8,求BE的长.
22、如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
(1)求证:DP∥AB;
(2)试猜想线段AE,EF,BF之间有何数量关系,并加以证明;
(3)若AC=6,BC=8,求线段PD的长.
参考答案
2020-2021学年北师大版九年级数学下册第三章
圆
单元复习同步练习题
一、选择题
1、如图,AB,CD是⊙O的直径,=.若∠AOE=32°,则∠COE的度数是(D)
A.32°
B.60°
C.68°
D.64°
2、如图,AB是⊙O的直径,∠BOD=120°,点C为的中点,AC交OD于点E,DE=1,则AE的长为(A)
A.
B.
C.2
D.2
3、如图,A,B,C,D是⊙O上的四个点,AB=AC,AD交BC于点E,AE=3,ED=4,则AC的长为(C)
A.3
B.2
C.
D.3
4、一根水平放置的圆柱形输水管的横截面如图所示,其中有水部分水面宽8米,最深处水深2米,则此输水管道的半径是(C)
A.8米
B.6米
C.5米
D.4米
5、如图,已知⊙O是正方形ABCD的外接圆,点E是上任意一点,则∠ABE+∠ECD的度数为(B)
A.30°
B.45°
C.60°
D.90°
6、如图,从一块直径为2
m的圆形铁皮上剪出一个圆心角为90°的扇形,则此扇形的面积为(A)
A.
m2
B.π
m2
C.π
m2
D.2π
m2
7、如图所示,在⊙O中,AB为弦,OC⊥AB交AB于点D,且OD=DC.P为⊙O上任意一点,连接PA,PB.若⊙O的半径为1,则S△PAB的最大值为(C)
A.1
B.
C.
D.
8、如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.若CD=,则图中阴影部分面积为(B)
A.4-
B.2-
C.2-π
D.1-
二、填空题
9、如图,圆内接四边形ABCD中,∠BCD=90°,AB=AD,点E在CD的延长线上,且DE=BC,连接AE.若AE=4,则四边形ABCD的面积为8.
10、如图,已知BD是⊙O的直径,点A,C在⊙O上,=,∠AOB=60°,则∠COD的度数是120°.
11、如图,△ABC是圆的内接三角形,点P是△ABC的内心,∠A=50°,则∠BPC的度数为115°.
12、如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,则∠A的度数是28°.
13、如图,在平行四边形ABCD中,AB<AD,∠D=30°,CD=4,以AB为直径的⊙O交BC于点E,则阴影部分的面积为π-.
三、解答题
14、如图,△ABE内接于⊙O,过直径AB上的点G作弦CD⊥AB,交AE于点F,连接AD,DE.
求证:
△ADF∽△AED.
证明:∵AB是⊙O的直径,CD⊥AB,
∴=.
∴∠ADF=∠AED.
∵∠FAD=∠DAE,
∴△ADF∽△AED.
15、如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD,CD.过点D作⊙O的切线交AC的延长线于点P.求证:△ABD∽△DCP.
证明:
连接OD,
∵BC是⊙O的直径,
∴∠BAC=90°.
∵AD平分∠BAC,
∴∠BAC=2∠BAD.
∵∠BOD=2∠BAD,
∴∠BOD=∠BAC=90°.
∵DP为⊙O的切线,
∴PD⊥OD.
∴PD∥BC.
∴∠ACB=∠P.
∵∠ACB=∠ADB,
∴∠ADB=∠P.
∵∠ABD+∠ACD=180°,∠ACD+∠DCP=
180°,
∴∠ABD=∠DCP.
∴△ABD∽△DCP.
16、如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接BD,BE.
(1)求证:△ABD∽△AEB;
(2)当=时,求tanE.
解:(1)∵∠ABC=90°,
∴∠ABD=90°-∠DBC.
由题意知:DE是直径,
∴∠DBE=90°.
∴∠E=90°-∠BDE.
∵BC=CD,
∴∠DBC=∠BDE.∴∠ABD=∠E.
∵∠A=∠A,∴△ABD∽△AEB.
(2)∵AB∶BC=4∶3,
∴设AB=4a,BC=3a,
∴AC==5a.
∵BC=CD=3a,
∴AD=AC-CD=2a.
由(1)可知:△ABD∽△AEB,
∴=.
在Rt△DBE中,
tanE====.
17、如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC,AB的延长线于点E,F.
(1)求证:EF是⊙O的切线;
(2)若AC=4,CE=2,求的长度.(结果保留π)
解:(1)连接OD,
∵OA=OD,
∴∠OAD=∠ODA.
∵AD平分∠EAF,
∴∠DAE=∠DAO.
∴∠DAE=∠ADO.∴OD∥AE.
∵AE⊥EF,∴OD⊥EF.
又∵OD是⊙O的半径,
∴EF是⊙O的切线.
(2)作OG⊥AE于点G,连接BD,
则AG=CG=AC=2,∠OGE=∠E=∠ODE=90°.
∴四边形ODEG是矩形.
∴OA=OB=OD=CG+CE=2+2=4,∠DOG=90°.
∵∠DAE=∠BAD,∠AED=∠ADB=90°,
∴△ADE∽△ABD.
∴=,即=.
∴AD=4.
在Rt△ABD中,cos∠BAD===,
∴∠BAD=30°.∴∠BOD=60°.
则的长度为=π.
18、如图,AB是⊙O的直径,点C是⊙O上一点,∠CAB的平分线AD交于点D,过点D作DE∥BC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)过点D作DF⊥AB于点F,连接BD.若OF=1,BF=2,求BD的长度.
解:(1)连接OD,
∵AB是⊙O的直径,
∴∠ACB=90°.
∵OA=OD,
∴∠OAD=∠ADO.
∵AD平分∠CAB,
∴∠DAE=∠OAD.
∴∠ADO=∠DAE.∴OD∥AE.
∵DE∥BC,∴∠E=∠ACB=90°.
∴∠ODE=180°-∠E=90°.
又∵OD是⊙O的半径,
∴DE是⊙O的切线.
(2)∵OF=1,BF=2,
∴OD=OB=3.
∵DF⊥AB,∴在Rt△ODF中,DF2=CD2-OF2=8.
在Rt△BDF中,BD==2.
19、如图,AB为⊙O的直径,C,D为圆上的两点,OC∥BD,弦AD,BC相交于点E.
(1)求证:=;
(2)若CE=1,EB=3,求⊙O的半径;
(3)在(2)的条件下,过点C作⊙O的切线,交BA的延长线于点P,过点P作PQ∥CB交⊙O于F,Q两点(点F在线段PQ上),求PQ的长.
解:(1)证明:∵OC=OB,
∴∠OBC=∠OCB.
∵OC∥BD,
∴∠OCB=∠CBD.
∴∠OBC=∠CBD.∴=.
(2)连接AC,∵CE=1,EB=3,∴BC=4.
∵=,
∴∠CAD=∠ABC.
又∵∠ACE=∠ACB.
∴△ACE∽△BCA.∴=.
∴AC2=CB·CE=4×1.∴AC=2.
∵AB是⊙O的直径,∴∠ACB=90°.
∴AB==2.
∴⊙O的半径为.
(3)过点O作OH⊥FQ于点H,连接OQ,
∵PC是⊙O切线,
∴∠PCO=90°,且∠ACB=90°.
∴∠PCA=∠BCO=∠CBO,且∠CPB=∠CPA.
∴△APC∽△CPB.
∴====.
∴PC=2PA,PC2=PA·PB.
∴4PA2=PA×(PA+2).
∴PA=.
∴PO=.
∵PQ∥BC,
∴∠CBA=∠BPQ.
又∵∠PHO=∠ACB=90°.
∴△PHO∽△BCA.
∴==,
即===.
∴PH=,OH=.
∴HQ==.
∴PQ=PH+HQ=.
20、如图,AB为⊙O直径,C,D是⊙O上的点,连接CB并延长与AD所在直线交于点F,EF⊥AB,垂足为E,连接CE,且CE=EF.
(1)证明:CE与⊙O相切;
(2)若AE=8,tan∠BCE=,求AD的长度.
解:(1)证明:连接OC,
∵AB为⊙O直径,
∴∠ACB=90°.
∵EF⊥AB,∴∠AEF=90°.
∴∠ACB=∠AEF.
∵∠ABC=∠EBF,∴∠CAB=∠EFB.
∵CE=EF,∴∠ECF=∠EFC.
∴∠CAB=∠ECF.
∵OC=OA,∴∠OAC=∠ACO.
∴∠ACO=∠ECF.
∴∠ACO+∠BCO=∠BCO+∠ECF=90°.
∴∠OCE=90°.
又∵OC是⊙O的半径,
∴CE与⊙O相切.
(2)∵∠CAB=∠BCE,
∴tan∠BCE=tan∠CAB==.
∵∠CEA=∠AEC,∴△ACE∽△CBE.
∴==.
∵AE=8,∴CE=4.
∴EF=CE=4.
∵∠EFB=∠CAB,
∴在Rt△BEF中,BE=EF·tan∠EFB=2.
∴AB=AE-BE=6.
连接BD,
∵AB为⊙O直径,∴∠ADB=90°.
∴tan∠BAD===.
设AD=2k,BD=k,
∴AB=k=6.∴k=.
∴AD=2k=.
21、如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)求证:CG=BG;
(3)若∠DBA=30°,CG=8,求BE的长.
解:(1)证明:连接OC,
∵∠A=∠CBD,
∴=.
∴OC⊥BD.
∵CE∥BD,∴OC⊥CE.
又∵OC是⊙O的半径,
∴CE是⊙O的切线.
(2)证明:∵AB为直径,∴∠ACB=90°.
∵CF⊥AB,∴∠ACB=∠CFB=90°.
∵∠ABC=∠CBF,∴∠A=∠BCF.
∵∠A=∠CBD,∴∠BCF=∠CBD.
∴CG=BG.
(3)连接AD,
∵AB为直径,∴∠ADB=90°.
∵∠DBA=30°,∴∠BAD=60°.
∵=,
∴∠DAC=∠BAC=∠BAD=30°.
∴=tan30°=.
∵CE∥BD,∴∠E=∠DBA=30°.
∴AC=CE.
∴=.
∵∠A=∠BCF=∠CBD=30°,
∴∠BCE=30°.
∴BE=BC.∴△CGB∽△CBE.
∴==.
∵CG=8,∴BC=8.
∴BE=8.
22、如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
(1)求证:DP∥AB;
(2)试猜想线段AE,EF,BF之间有何数量关系,并加以证明;
(3)若AC=6,BC=8,求线段PD的长.
解:(1)证明:连接OD,
∵AB为⊙O的直径,
∴∠ACB=90°.
∵∠ACB的平分线交⊙O于点D,
∴∠ACD=∠BCD=45°.
∴∠AOD=2∠ACD=90°.
∵PD为⊙O的切线,
∴OD⊥PD,即∠ODP=90°.
∴∠AOD+∠ODP=180°.
∴DP∥AB.
(2)BF-AE=EF,证明如下:
∵AB是⊙O的直径,
∴∠ADB=∠ADE+∠BDF=90°.
∵AE⊥CD,BF⊥CD,∴∠AED=∠BFD=90°.
∴∠FBD+∠BDF=90°.
∴∠FBD=∠ADE.
∵∠ACD=∠BCD,∴AD=BD.
在△ADE和△DBF中,
∴△ADE≌△DBF(AAS).
∴BF=DE,AE=DF.
∴BF-AE=DE-DF=EF.
(3)在Rt△ACB中,AB==10,
∵△DAB为等腰直角三角形,
∴AD=BD===5.
∵AE⊥CD,
∴△ACE为等腰直角三角形.
∴AE=CE===3.
在Rt△AED中,DE==(5)2-(3)2=4,
∴CD=CE+DE=3+4=7.
∵∠PDA=∠PCD,∠P=∠P,
∴△PDA∽△PCD.
∴====.
∴PA=PD,PC=PD.
又∵PC=PA+AC,
∴PD+6=PD,解得PD=.
圆
单元复习同步练习题
一、选择题
1、如图,AB,CD是⊙O的直径,=.若∠AOE=32°,则∠COE的度数是(
)
A.32°
B.60°
C.68°
D.64°
2、如图,AB是⊙O的直径,∠BOD=120°,点C为的中点,AC交OD于点E,DE=1,则AE的长为(
)
A.
B.
C.2
D.2
3、如图,A,B,C,D是⊙O上的四个点,AB=AC,AD交BC于点E,AE=3,ED=4,则AC的长为(
)
A.3
B.2
C.
D.3
4、一根水平放置的圆柱形输水管的横截面如图所示,其中有水部分水面宽8米,最深处水深2米,则此输水管道的半径是(
)
A.8米
B.6米
C.5米
D.4米
5、如图,已知⊙O是正方形ABCD的外接圆,点E是上任意一点,则∠ABE+∠ECD的度数为(
)
A.30°
B.45°
C.60°
D.90°
6、如图,从一块直径为2
m的圆形铁皮上剪出一个圆心角为90°的扇形,则此扇形的面积为(
)
A.
m2
B.π
m2
C.π
m2
D.2π
m2
7、如图所示,在⊙O中,AB为弦,OC⊥AB交AB于点D,且OD=DC.P为⊙O上任意一点,连接PA,PB.若⊙O的半径为1,则S△PAB的最大值为(
)
A.1
B.
C.
D.
8、如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.若CD=,则图中阴影部分面积为(
)
A.4-
B.2-
C.2-π
D.1-
二、填空题
9、如图,圆内接四边形ABCD中,∠BCD=90°,AB=AD,点E在CD的延长线上,且DE=BC,连接AE.若AE=4,则四边形ABCD的面积为______.
10、如图,已知BD是⊙O的直径,点A,C在⊙O上,=,∠AOB=60°,则∠COD的度数是______.
11、如图,△ABC是圆的内接三角形,点P是△ABC的内心,∠A=50°,则∠BPC的度数为______.
12、如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,则∠A的度数是______.
13、如图,在平行四边形ABCD中,AB<AD,∠D=30°,CD=4,以AB为直径的⊙O交BC于点E,则阴影部分的面积为______.
三、解答题
14、如图,△ABE内接于⊙O,过直径AB上的点G作弦CD⊥AB,交AE于点F,连接AD,DE.
求证:
△ADF∽△AED.
15、如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD,CD.过点D作⊙O的切线交AC的延长线于点P.求证:△ABD∽△DCP.
16、如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接BD,BE.
(1)求证:△ABD∽△AEB;
(2)当=时,求tanE.
17、如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC,AB的延长线于点E,F.
(1)求证:EF是⊙O的切线;
(2)若AC=4,CE=2,求的长度.(结果保留π)
18、如图,AB是⊙O的直径,点C是⊙O上一点,∠CAB的平分线AD交于点D,过点D作DE∥BC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)过点D作DF⊥AB于点F,连接BD.若OF=1,BF=2,求BD的长度.
19、如图,AB为⊙O的直径,C,D为圆上的两点,OC∥BD,弦AD,BC相交于点E.
(1)求证:=;
(2)若CE=1,EB=3,求⊙O的半径;
(3)在(2)的条件下,过点C作⊙O的切线,交BA的延长线于点P,过点P作PQ∥CB交⊙O于F,Q两点(点F在线段PQ上),求PQ的长.
20、如图,AB为⊙O直径,C,D是⊙O上的点,连接CB并延长与AD所在直线交于点F,EF⊥AB,垂足为E,连接CE,且CE=EF.
(1)证明:CE与⊙O相切;
(2)若AE=8,tan∠BCE=,求AD的长度.
21、如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)求证:CG=BG;
(3)若∠DBA=30°,CG=8,求BE的长.
22、如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
(1)求证:DP∥AB;
(2)试猜想线段AE,EF,BF之间有何数量关系,并加以证明;
(3)若AC=6,BC=8,求线段PD的长.
参考答案
2020-2021学年北师大版九年级数学下册第三章
圆
单元复习同步练习题
一、选择题
1、如图,AB,CD是⊙O的直径,=.若∠AOE=32°,则∠COE的度数是(D)
A.32°
B.60°
C.68°
D.64°
2、如图,AB是⊙O的直径,∠BOD=120°,点C为的中点,AC交OD于点E,DE=1,则AE的长为(A)
A.
B.
C.2
D.2
3、如图,A,B,C,D是⊙O上的四个点,AB=AC,AD交BC于点E,AE=3,ED=4,则AC的长为(C)
A.3
B.2
C.
D.3
4、一根水平放置的圆柱形输水管的横截面如图所示,其中有水部分水面宽8米,最深处水深2米,则此输水管道的半径是(C)
A.8米
B.6米
C.5米
D.4米
5、如图,已知⊙O是正方形ABCD的外接圆,点E是上任意一点,则∠ABE+∠ECD的度数为(B)
A.30°
B.45°
C.60°
D.90°
6、如图,从一块直径为2
m的圆形铁皮上剪出一个圆心角为90°的扇形,则此扇形的面积为(A)
A.
m2
B.π
m2
C.π
m2
D.2π
m2
7、如图所示,在⊙O中,AB为弦,OC⊥AB交AB于点D,且OD=DC.P为⊙O上任意一点,连接PA,PB.若⊙O的半径为1,则S△PAB的最大值为(C)
A.1
B.
C.
D.
8、如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.若CD=,则图中阴影部分面积为(B)
A.4-
B.2-
C.2-π
D.1-
二、填空题
9、如图,圆内接四边形ABCD中,∠BCD=90°,AB=AD,点E在CD的延长线上,且DE=BC,连接AE.若AE=4,则四边形ABCD的面积为8.
10、如图,已知BD是⊙O的直径,点A,C在⊙O上,=,∠AOB=60°,则∠COD的度数是120°.
11、如图,△ABC是圆的内接三角形,点P是△ABC的内心,∠A=50°,则∠BPC的度数为115°.
12、如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,则∠A的度数是28°.
13、如图,在平行四边形ABCD中,AB<AD,∠D=30°,CD=4,以AB为直径的⊙O交BC于点E,则阴影部分的面积为π-.
三、解答题
14、如图,△ABE内接于⊙O,过直径AB上的点G作弦CD⊥AB,交AE于点F,连接AD,DE.
求证:
△ADF∽△AED.
证明:∵AB是⊙O的直径,CD⊥AB,
∴=.
∴∠ADF=∠AED.
∵∠FAD=∠DAE,
∴△ADF∽△AED.
15、如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD,CD.过点D作⊙O的切线交AC的延长线于点P.求证:△ABD∽△DCP.
证明:
连接OD,
∵BC是⊙O的直径,
∴∠BAC=90°.
∵AD平分∠BAC,
∴∠BAC=2∠BAD.
∵∠BOD=2∠BAD,
∴∠BOD=∠BAC=90°.
∵DP为⊙O的切线,
∴PD⊥OD.
∴PD∥BC.
∴∠ACB=∠P.
∵∠ACB=∠ADB,
∴∠ADB=∠P.
∵∠ABD+∠ACD=180°,∠ACD+∠DCP=
180°,
∴∠ABD=∠DCP.
∴△ABD∽△DCP.
16、如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接BD,BE.
(1)求证:△ABD∽△AEB;
(2)当=时,求tanE.
解:(1)∵∠ABC=90°,
∴∠ABD=90°-∠DBC.
由题意知:DE是直径,
∴∠DBE=90°.
∴∠E=90°-∠BDE.
∵BC=CD,
∴∠DBC=∠BDE.∴∠ABD=∠E.
∵∠A=∠A,∴△ABD∽△AEB.
(2)∵AB∶BC=4∶3,
∴设AB=4a,BC=3a,
∴AC==5a.
∵BC=CD=3a,
∴AD=AC-CD=2a.
由(1)可知:△ABD∽△AEB,
∴=.
在Rt△DBE中,
tanE====.
17、如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC,AB的延长线于点E,F.
(1)求证:EF是⊙O的切线;
(2)若AC=4,CE=2,求的长度.(结果保留π)
解:(1)连接OD,
∵OA=OD,
∴∠OAD=∠ODA.
∵AD平分∠EAF,
∴∠DAE=∠DAO.
∴∠DAE=∠ADO.∴OD∥AE.
∵AE⊥EF,∴OD⊥EF.
又∵OD是⊙O的半径,
∴EF是⊙O的切线.
(2)作OG⊥AE于点G,连接BD,
则AG=CG=AC=2,∠OGE=∠E=∠ODE=90°.
∴四边形ODEG是矩形.
∴OA=OB=OD=CG+CE=2+2=4,∠DOG=90°.
∵∠DAE=∠BAD,∠AED=∠ADB=90°,
∴△ADE∽△ABD.
∴=,即=.
∴AD=4.
在Rt△ABD中,cos∠BAD===,
∴∠BAD=30°.∴∠BOD=60°.
则的长度为=π.
18、如图,AB是⊙O的直径,点C是⊙O上一点,∠CAB的平分线AD交于点D,过点D作DE∥BC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)过点D作DF⊥AB于点F,连接BD.若OF=1,BF=2,求BD的长度.
解:(1)连接OD,
∵AB是⊙O的直径,
∴∠ACB=90°.
∵OA=OD,
∴∠OAD=∠ADO.
∵AD平分∠CAB,
∴∠DAE=∠OAD.
∴∠ADO=∠DAE.∴OD∥AE.
∵DE∥BC,∴∠E=∠ACB=90°.
∴∠ODE=180°-∠E=90°.
又∵OD是⊙O的半径,
∴DE是⊙O的切线.
(2)∵OF=1,BF=2,
∴OD=OB=3.
∵DF⊥AB,∴在Rt△ODF中,DF2=CD2-OF2=8.
在Rt△BDF中,BD==2.
19、如图,AB为⊙O的直径,C,D为圆上的两点,OC∥BD,弦AD,BC相交于点E.
(1)求证:=;
(2)若CE=1,EB=3,求⊙O的半径;
(3)在(2)的条件下,过点C作⊙O的切线,交BA的延长线于点P,过点P作PQ∥CB交⊙O于F,Q两点(点F在线段PQ上),求PQ的长.
解:(1)证明:∵OC=OB,
∴∠OBC=∠OCB.
∵OC∥BD,
∴∠OCB=∠CBD.
∴∠OBC=∠CBD.∴=.
(2)连接AC,∵CE=1,EB=3,∴BC=4.
∵=,
∴∠CAD=∠ABC.
又∵∠ACE=∠ACB.
∴△ACE∽△BCA.∴=.
∴AC2=CB·CE=4×1.∴AC=2.
∵AB是⊙O的直径,∴∠ACB=90°.
∴AB==2.
∴⊙O的半径为.
(3)过点O作OH⊥FQ于点H,连接OQ,
∵PC是⊙O切线,
∴∠PCO=90°,且∠ACB=90°.
∴∠PCA=∠BCO=∠CBO,且∠CPB=∠CPA.
∴△APC∽△CPB.
∴====.
∴PC=2PA,PC2=PA·PB.
∴4PA2=PA×(PA+2).
∴PA=.
∴PO=.
∵PQ∥BC,
∴∠CBA=∠BPQ.
又∵∠PHO=∠ACB=90°.
∴△PHO∽△BCA.
∴==,
即===.
∴PH=,OH=.
∴HQ==.
∴PQ=PH+HQ=.
20、如图,AB为⊙O直径,C,D是⊙O上的点,连接CB并延长与AD所在直线交于点F,EF⊥AB,垂足为E,连接CE,且CE=EF.
(1)证明:CE与⊙O相切;
(2)若AE=8,tan∠BCE=,求AD的长度.
解:(1)证明:连接OC,
∵AB为⊙O直径,
∴∠ACB=90°.
∵EF⊥AB,∴∠AEF=90°.
∴∠ACB=∠AEF.
∵∠ABC=∠EBF,∴∠CAB=∠EFB.
∵CE=EF,∴∠ECF=∠EFC.
∴∠CAB=∠ECF.
∵OC=OA,∴∠OAC=∠ACO.
∴∠ACO=∠ECF.
∴∠ACO+∠BCO=∠BCO+∠ECF=90°.
∴∠OCE=90°.
又∵OC是⊙O的半径,
∴CE与⊙O相切.
(2)∵∠CAB=∠BCE,
∴tan∠BCE=tan∠CAB==.
∵∠CEA=∠AEC,∴△ACE∽△CBE.
∴==.
∵AE=8,∴CE=4.
∴EF=CE=4.
∵∠EFB=∠CAB,
∴在Rt△BEF中,BE=EF·tan∠EFB=2.
∴AB=AE-BE=6.
连接BD,
∵AB为⊙O直径,∴∠ADB=90°.
∴tan∠BAD===.
设AD=2k,BD=k,
∴AB=k=6.∴k=.
∴AD=2k=.
21、如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)求证:CG=BG;
(3)若∠DBA=30°,CG=8,求BE的长.
解:(1)证明:连接OC,
∵∠A=∠CBD,
∴=.
∴OC⊥BD.
∵CE∥BD,∴OC⊥CE.
又∵OC是⊙O的半径,
∴CE是⊙O的切线.
(2)证明:∵AB为直径,∴∠ACB=90°.
∵CF⊥AB,∴∠ACB=∠CFB=90°.
∵∠ABC=∠CBF,∴∠A=∠BCF.
∵∠A=∠CBD,∴∠BCF=∠CBD.
∴CG=BG.
(3)连接AD,
∵AB为直径,∴∠ADB=90°.
∵∠DBA=30°,∴∠BAD=60°.
∵=,
∴∠DAC=∠BAC=∠BAD=30°.
∴=tan30°=.
∵CE∥BD,∴∠E=∠DBA=30°.
∴AC=CE.
∴=.
∵∠A=∠BCF=∠CBD=30°,
∴∠BCE=30°.
∴BE=BC.∴△CGB∽△CBE.
∴==.
∵CG=8,∴BC=8.
∴BE=8.
22、如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
(1)求证:DP∥AB;
(2)试猜想线段AE,EF,BF之间有何数量关系,并加以证明;
(3)若AC=6,BC=8,求线段PD的长.
解:(1)证明:连接OD,
∵AB为⊙O的直径,
∴∠ACB=90°.
∵∠ACB的平分线交⊙O于点D,
∴∠ACD=∠BCD=45°.
∴∠AOD=2∠ACD=90°.
∵PD为⊙O的切线,
∴OD⊥PD,即∠ODP=90°.
∴∠AOD+∠ODP=180°.
∴DP∥AB.
(2)BF-AE=EF,证明如下:
∵AB是⊙O的直径,
∴∠ADB=∠ADE+∠BDF=90°.
∵AE⊥CD,BF⊥CD,∴∠AED=∠BFD=90°.
∴∠FBD+∠BDF=90°.
∴∠FBD=∠ADE.
∵∠ACD=∠BCD,∴AD=BD.
在△ADE和△DBF中,
∴△ADE≌△DBF(AAS).
∴BF=DE,AE=DF.
∴BF-AE=DE-DF=EF.
(3)在Rt△ACB中,AB==10,
∵△DAB为等腰直角三角形,
∴AD=BD===5.
∵AE⊥CD,
∴△ACE为等腰直角三角形.
∴AE=CE===3.
在Rt△AED中,DE==(5)2-(3)2=4,
∴CD=CE+DE=3+4=7.
∵∠PDA=∠PCD,∠P=∠P,
∴△PDA∽△PCD.
∴====.
∴PA=PD,PC=PD.
又∵PC=PA+AC,
∴PD+6=PD,解得PD=.
