2020-2021学年人教版九年级数学下册 第27章 相似 同步单元训练卷(Word版 含答案)
文档属性
| 名称 | 2020-2021学年人教版九年级数学下册 第27章 相似 同步单元训练卷(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 285.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-28 23:02:28 | ||
图片预览


文档简介
人教版九年级数学下册
第27章
相似
同步单元训练卷
一、选择题(共10小题,3
10=30)
1.下列各组图形相似的是( )
2.如图,在△ABC中,D,E分别为AB,AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )
A.=
B.=
C.=
D.=
3.如图,已知△ABC与△BDE都是等边三角形,点D在边AC上(不与点A,C重合),DE与AB相交于点F,那么与△BFD相似的三角形是( )
A.△BFE
B.△BDC
C.△BDA
D.△AFD
4.如图,在平面直角坐标系中,有点A(6,3),B(6,0),以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
A.(2,1)
B.(3,2)
C.(3,3)
D.(3,1)
5.如图,△ABO∽△CDO,若BO=6,DO=3,CD=2,则AB的长是(
)
A.2
B.3
C.4
D.5
6.
下列说法:①有一个角等于30°的两个等腰三角形相似;
②有一个角等于120°的两个等腰三角形相似;
③相似三角形一定不是全等三角形;
④相似三角形对应角平分线的长度比等于面积比.
其中正确的个数是( )
A.1
B.2
C.3
D.4
7.
如图,在平行四边形ABCD中,点E在边DC上,DE∶EC=3∶1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
A.3∶4
B.9∶16
C.9∶1
D.3∶1
8.如图,在平面直角坐标系中,直线y=-x+3与x轴、y轴分别交于点A和点B,C是线段AB上一点.过点C作CD⊥x轴,垂足为D,CE⊥y轴,垂足为E,S△BEC∶S△CDA=4∶1,若双曲线y=(x>0)经过点C,则k的值为( )
A.
B.
C.
D.
9.如图,AB为⊙O的直径,BC为⊙O的切线,弦AD∥OC,直线CD交BA的延长线于点E,连接BD.下列结论:①CD是⊙O的切线;②CO⊥DB;③△EDA∽△EBD;④ED·BC=BO·BE.其中正确结论的个数有( )
A.4个
B.3个
C.2个
D.1个
10.如图所示,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20
m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5
m,两个路灯的高度是9
m,则两路灯之间的距离是( )
A.24
m
B.25
m
C.28
m
D.30
m
二.填空题(共8小题,3
8=24)
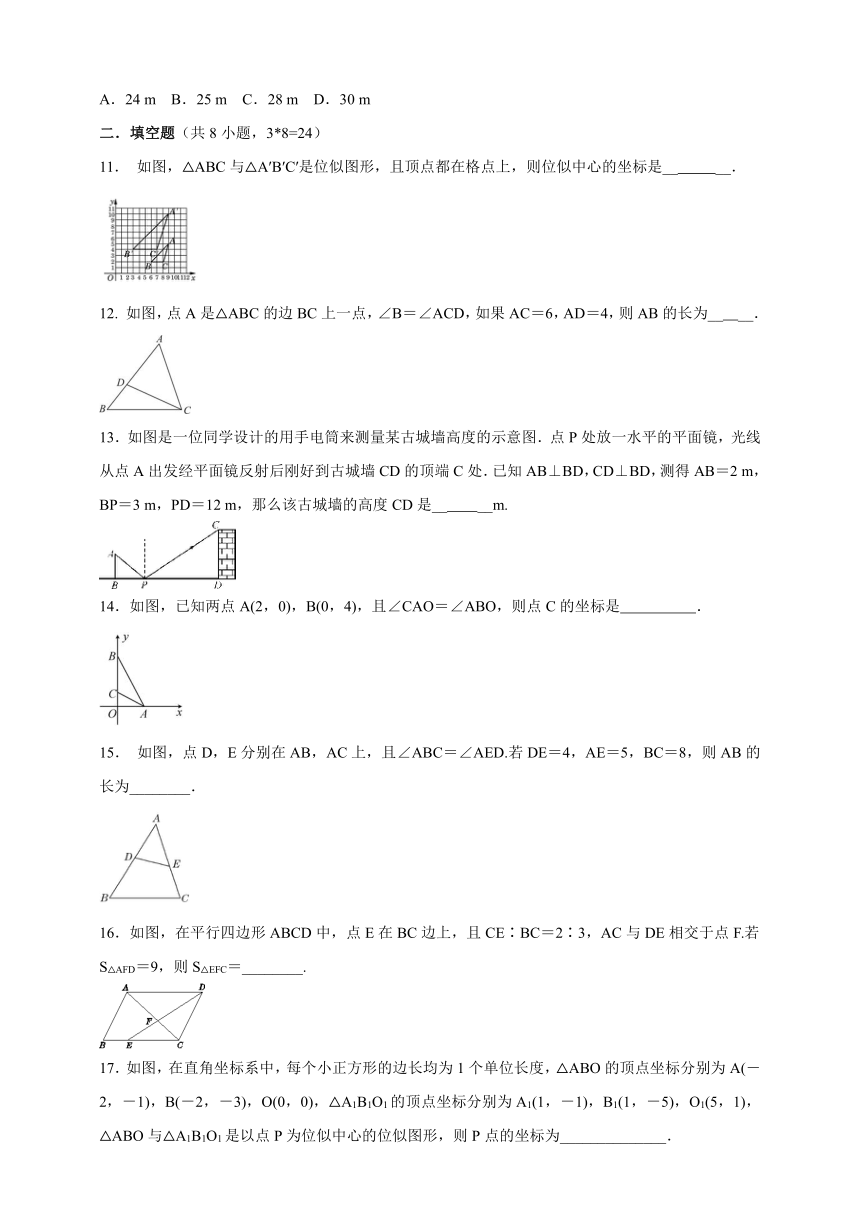
11.
如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,则位似中心的坐标是__
__.
12.
如图,点A是△ABC的边BC上一点,∠B=∠ACD,如果AC=6,AD=4,则AB的长为__
__.
13.如图是一位同学设计的用手电筒来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD,测得AB=2
m,BP=3
m,PD=12
m,那么该古城墙的高度CD是__
__m.
14.如图,已知两点A(2,0),B(0,4),且∠CAO=∠ABO,则点C的坐标是
.
15.
如图,点D,E分别在AB,AC上,且∠ABC=∠AED.若DE=4,AE=5,BC=8,则AB的长为________.
16.如图,在平行四边形ABCD中,点E在BC边上,且CE∶BC=2∶3,AC与DE相交于点F.若S△AFD=9,则S△EFC=________.
17.如图,在直角坐标系中,每个小正方形的边长均为1个单位长度,△ABO的顶点坐标分别为A(-2,-1),B(-2,-3),O(0,0),△A1B1O1的顶点坐标分别为A1(1,-1),B1(1,-5),O1(5,1),△ABO与△A1B1O1是以点P为位似中心的位似图形,则P点的坐标为______________.
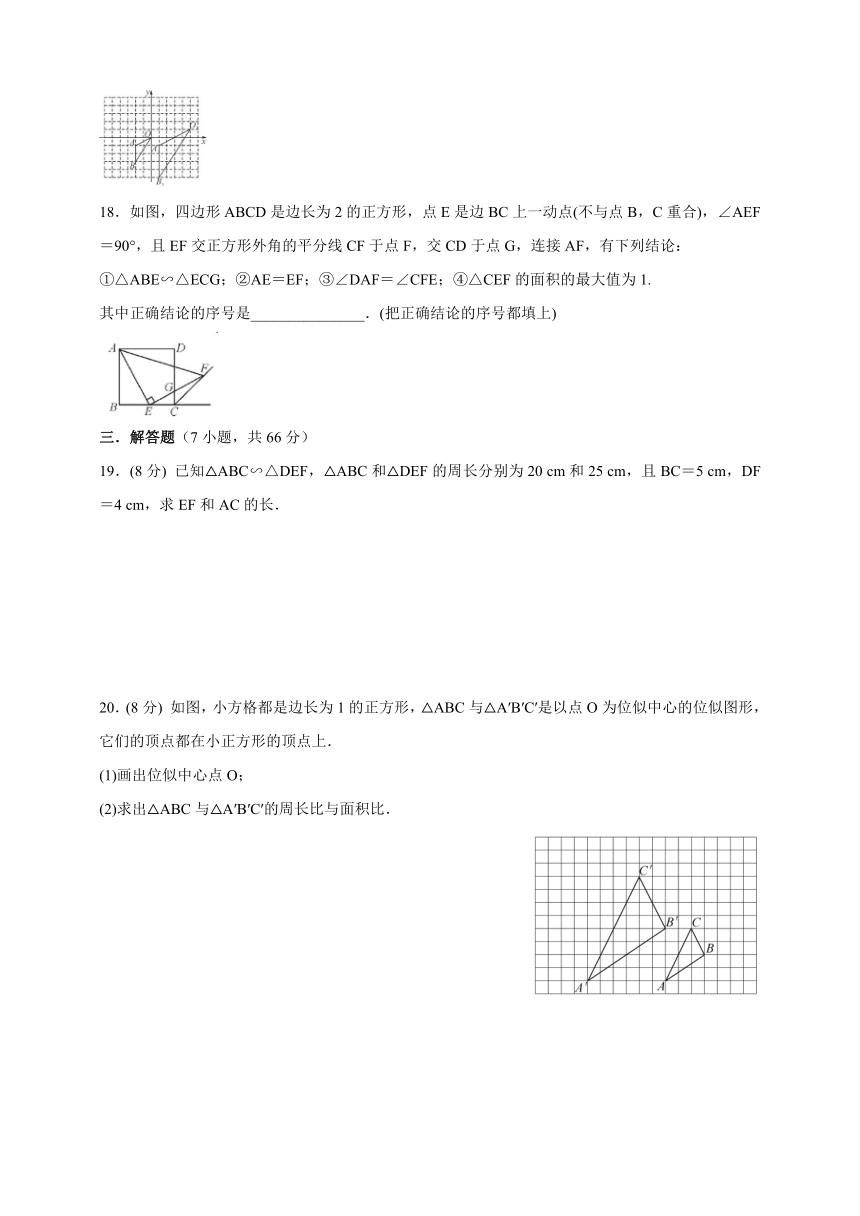
18.如图,四边形ABCD是边长为2的正方形,点E是边BC上一动点(不与点B,C重合),∠AEF=90°,且EF交正方形外角的平分线CF于点F,交CD于点G,连接AF,有下列结论:
①△ABE∽△ECG;②AE=EF;③∠DAF=∠CFE;④△CEF的面积的最大值为1.
其中正确结论的序号是_______________.(把正确结论的序号都填上)
三.解答题(7小题,共66分)
19.(8分)
已知△ABC∽△DEF,△ABC和△DEF的周长分别为20
cm和25
cm,且BC=5
cm,DF=4
cm,求EF和AC的长.
20.(8分)
如图,小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点O;
(2)求出△ABC与△A′B′C′的周长比与面积比.
21.(8分)
如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1
m,继续往前走3
m到达E处时,测得影子EF的长为2
m,已知王华的身高是1.5
m.求路灯A的高度.
22.(10分)
如图,已知B,C,E三点在同一条直线上,△ABC与△DCE都是等边三角形,其中线段BD交AC于点G,线段AE交CD于点F.求证:(1)△ACE≌△BCD;(2)=.
23.(10分)
如图,在Rt△ABC中,∠C=90°,点O在AC上,以OA为半径的半圆O交AB于点D,交AC于点E,过点D作半圆O的切线DF,交BC于点F.
(1)求证:BF=DF;
(2)若AC=4,BC=3,CF=1,求半圆O的半径长.
24.(10分)
如图,在△ABC中,AB=10
cm,BC=20
cm,点P从点A开始沿AB边以2
cm/s的速度向点B移动,点Q从点B开始沿BC边以4
cm/s的速度向点C移动,如果点P,Q分别从A,B同时出发,问经过多久,△PBQ与△ABC相似?
25.(12分)
如图,AB为⊙O的直径,点P在AB的延长线上,点C在⊙O上,且PC2=PB·PA.
(1)求证:PC是⊙O的切线;
(2)已知PC=20,PB=10,点D是\s\up8(︵(︵)的中点,DE⊥AC,垂足为E,DE交AB于点F,求EF的长.
参考答案
1-5BCCAC
6-10ABAAD
11.
(9,0)
12.
9
13.
8
14.
(0,1)
15.10 16.4
17.
(-5,-1)
18.
①②③
19.
解:∵△ABC∽△DEF,∴==,∴==,∴AC=
cm,EF=
cm
20.
解:(1)连接B′B,C′C并延长相交于一点,此点即为位似中心点O,图略.(2)由图形,得AB==,A′B′==2,∴△ABC与△A′B′C′的周长比为1∶2,面积比为1∶4.
21.
解:由题意,得CD=1
m,CE=3
m,EF=2
m,MC=NE=1.5
m,AB∥MC∥NE,∴△ABD∽△MCD,△ABF∽△NEF,∴=,=,即=,=,解得AB=6
m,BC=3
m,∴路灯A的高度为6
m
22.
解:(1)∵△ABC与△CDE都是等边三角形,∴AC=BC,CE=CD,∠ACB=∠DCE=60°,∴∠ACB+∠ACD=∠DCE+∠ACD,即∠ACE=∠BCD,可证△ACE≌△BCD(SAS) (2)∵△ACE≌△BCD,∴∠AEC=∠BDC,可证△GCD≌△FCE(ASA),∴CG=CF,∴△CFG为等边三角形,∴∠CGF=∠ACB=60°,∴GF∥CE,∴=
23.
解:(1)连接OD,如图①,∵过点D作半圆O的切线DF,交BC于点F,∴∠ODF=90°,∴∠ADO+∠BDF=90°,∵OA=OD,∴∠OAD=∠ODA,∴∠OAD+∠BDF=90°,∵∠C=90°,∴∠OAD+∠B=90°,∴∠B=∠BDF,∴BF=DF (2)连接OF,如图②,设圆的半径为r,则OD=OE=r,∵AC=4,BC=3,CF=1,∴OC=4-r,DF=BF=3-1=2,∵OD2+DF2=OF2=OC2+CF2,∴r2+22=(4-r)2+12,∴r=,故圆的半径为
24.
解:设经过t
s,△PBQ与△ABC相似.则AP=2t
cm,BQ=4t
cm,BP=(10-2t)cm.
当△PBQ∽△ABC时,有=,即=,解得t=2.5.
当△QBP∽△ABC时,有=,即=,解得t=1.
综上所述,经过2.5
s或1
s,△PBQ与△ABC相似.
25.
解:(1)连接OC,如图①所示:∵PC2=PB·PA,即=,∵∠P=∠P,∴△PBC∽△PCA,∴∠PCB=∠PAC,∵AB为⊙O的直径,∴∠ACB=90°,∴∠A+∠ABC=90°,∵OC=OB,∴∠OBC=∠OCB,∴∠PCB+∠OCB=90°,即OC⊥PC,∴PC是⊙O的切线
(2)连接OD,如图②所示:∵PC=20,PB=10,PC2=PB·PA,∴PA===40,∴AB=PA-PB=30,∵△PBC∽△PCA,∴==2,设BC=x,则AC=2x,在Rt△ABC中,x2+(2x)2=302,解得:x=6,即BC=6,∵点D是\s\up8(︵(︵)的中点,AB为⊙O的直径,∴∠AOD=90°,∵DE⊥AC,∴∠AEF=90°,∵∠ACB=90°,∴DE∥BC,∴∠DFO=∠ABC,∴△DOF∽△ACB,∴==,∴OF=OD=,即AF=,∵EF∥BC,∴==,∴EF=BC=
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
第27章
相似
同步单元训练卷
一、选择题(共10小题,3
10=30)
1.下列各组图形相似的是( )
2.如图,在△ABC中,D,E分别为AB,AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )
A.=
B.=
C.=
D.=
3.如图,已知△ABC与△BDE都是等边三角形,点D在边AC上(不与点A,C重合),DE与AB相交于点F,那么与△BFD相似的三角形是( )
A.△BFE
B.△BDC
C.△BDA
D.△AFD
4.如图,在平面直角坐标系中,有点A(6,3),B(6,0),以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
A.(2,1)
B.(3,2)
C.(3,3)
D.(3,1)
5.如图,△ABO∽△CDO,若BO=6,DO=3,CD=2,则AB的长是(
)
A.2
B.3
C.4
D.5
6.
下列说法:①有一个角等于30°的两个等腰三角形相似;
②有一个角等于120°的两个等腰三角形相似;
③相似三角形一定不是全等三角形;
④相似三角形对应角平分线的长度比等于面积比.
其中正确的个数是( )
A.1
B.2
C.3
D.4
7.
如图,在平行四边形ABCD中,点E在边DC上,DE∶EC=3∶1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
A.3∶4
B.9∶16
C.9∶1
D.3∶1
8.如图,在平面直角坐标系中,直线y=-x+3与x轴、y轴分别交于点A和点B,C是线段AB上一点.过点C作CD⊥x轴,垂足为D,CE⊥y轴,垂足为E,S△BEC∶S△CDA=4∶1,若双曲线y=(x>0)经过点C,则k的值为( )
A.
B.
C.
D.
9.如图,AB为⊙O的直径,BC为⊙O的切线,弦AD∥OC,直线CD交BA的延长线于点E,连接BD.下列结论:①CD是⊙O的切线;②CO⊥DB;③△EDA∽△EBD;④ED·BC=BO·BE.其中正确结论的个数有( )
A.4个
B.3个
C.2个
D.1个
10.如图所示,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20
m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5
m,两个路灯的高度是9
m,则两路灯之间的距离是( )
A.24
m
B.25
m
C.28
m
D.30
m
二.填空题(共8小题,3
8=24)
11.
如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,则位似中心的坐标是__
__.
12.
如图,点A是△ABC的边BC上一点,∠B=∠ACD,如果AC=6,AD=4,则AB的长为__
__.
13.如图是一位同学设计的用手电筒来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD,测得AB=2
m,BP=3
m,PD=12
m,那么该古城墙的高度CD是__
__m.
14.如图,已知两点A(2,0),B(0,4),且∠CAO=∠ABO,则点C的坐标是
.
15.
如图,点D,E分别在AB,AC上,且∠ABC=∠AED.若DE=4,AE=5,BC=8,则AB的长为________.
16.如图,在平行四边形ABCD中,点E在BC边上,且CE∶BC=2∶3,AC与DE相交于点F.若S△AFD=9,则S△EFC=________.
17.如图,在直角坐标系中,每个小正方形的边长均为1个单位长度,△ABO的顶点坐标分别为A(-2,-1),B(-2,-3),O(0,0),△A1B1O1的顶点坐标分别为A1(1,-1),B1(1,-5),O1(5,1),△ABO与△A1B1O1是以点P为位似中心的位似图形,则P点的坐标为______________.
18.如图,四边形ABCD是边长为2的正方形,点E是边BC上一动点(不与点B,C重合),∠AEF=90°,且EF交正方形外角的平分线CF于点F,交CD于点G,连接AF,有下列结论:
①△ABE∽△ECG;②AE=EF;③∠DAF=∠CFE;④△CEF的面积的最大值为1.
其中正确结论的序号是_______________.(把正确结论的序号都填上)
三.解答题(7小题,共66分)
19.(8分)
已知△ABC∽△DEF,△ABC和△DEF的周长分别为20
cm和25
cm,且BC=5
cm,DF=4
cm,求EF和AC的长.
20.(8分)
如图,小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点O;
(2)求出△ABC与△A′B′C′的周长比与面积比.
21.(8分)
如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1
m,继续往前走3
m到达E处时,测得影子EF的长为2
m,已知王华的身高是1.5
m.求路灯A的高度.
22.(10分)
如图,已知B,C,E三点在同一条直线上,△ABC与△DCE都是等边三角形,其中线段BD交AC于点G,线段AE交CD于点F.求证:(1)△ACE≌△BCD;(2)=.
23.(10分)
如图,在Rt△ABC中,∠C=90°,点O在AC上,以OA为半径的半圆O交AB于点D,交AC于点E,过点D作半圆O的切线DF,交BC于点F.
(1)求证:BF=DF;
(2)若AC=4,BC=3,CF=1,求半圆O的半径长.
24.(10分)
如图,在△ABC中,AB=10
cm,BC=20
cm,点P从点A开始沿AB边以2
cm/s的速度向点B移动,点Q从点B开始沿BC边以4
cm/s的速度向点C移动,如果点P,Q分别从A,B同时出发,问经过多久,△PBQ与△ABC相似?
25.(12分)
如图,AB为⊙O的直径,点P在AB的延长线上,点C在⊙O上,且PC2=PB·PA.
(1)求证:PC是⊙O的切线;
(2)已知PC=20,PB=10,点D是\s\up8(︵(︵)的中点,DE⊥AC,垂足为E,DE交AB于点F,求EF的长.
参考答案
1-5BCCAC
6-10ABAAD
11.
(9,0)
12.
9
13.
8
14.
(0,1)
15.10 16.4
17.
(-5,-1)
18.
①②③
19.
解:∵△ABC∽△DEF,∴==,∴==,∴AC=
cm,EF=
cm
20.
解:(1)连接B′B,C′C并延长相交于一点,此点即为位似中心点O,图略.(2)由图形,得AB==,A′B′==2,∴△ABC与△A′B′C′的周长比为1∶2,面积比为1∶4.
21.
解:由题意,得CD=1
m,CE=3
m,EF=2
m,MC=NE=1.5
m,AB∥MC∥NE,∴△ABD∽△MCD,△ABF∽△NEF,∴=,=,即=,=,解得AB=6
m,BC=3
m,∴路灯A的高度为6
m
22.
解:(1)∵△ABC与△CDE都是等边三角形,∴AC=BC,CE=CD,∠ACB=∠DCE=60°,∴∠ACB+∠ACD=∠DCE+∠ACD,即∠ACE=∠BCD,可证△ACE≌△BCD(SAS) (2)∵△ACE≌△BCD,∴∠AEC=∠BDC,可证△GCD≌△FCE(ASA),∴CG=CF,∴△CFG为等边三角形,∴∠CGF=∠ACB=60°,∴GF∥CE,∴=
23.
解:(1)连接OD,如图①,∵过点D作半圆O的切线DF,交BC于点F,∴∠ODF=90°,∴∠ADO+∠BDF=90°,∵OA=OD,∴∠OAD=∠ODA,∴∠OAD+∠BDF=90°,∵∠C=90°,∴∠OAD+∠B=90°,∴∠B=∠BDF,∴BF=DF (2)连接OF,如图②,设圆的半径为r,则OD=OE=r,∵AC=4,BC=3,CF=1,∴OC=4-r,DF=BF=3-1=2,∵OD2+DF2=OF2=OC2+CF2,∴r2+22=(4-r)2+12,∴r=,故圆的半径为
24.
解:设经过t
s,△PBQ与△ABC相似.则AP=2t
cm,BQ=4t
cm,BP=(10-2t)cm.
当△PBQ∽△ABC时,有=,即=,解得t=2.5.
当△QBP∽△ABC时,有=,即=,解得t=1.
综上所述,经过2.5
s或1
s,△PBQ与△ABC相似.
25.
解:(1)连接OC,如图①所示:∵PC2=PB·PA,即=,∵∠P=∠P,∴△PBC∽△PCA,∴∠PCB=∠PAC,∵AB为⊙O的直径,∴∠ACB=90°,∴∠A+∠ABC=90°,∵OC=OB,∴∠OBC=∠OCB,∴∠PCB+∠OCB=90°,即OC⊥PC,∴PC是⊙O的切线
(2)连接OD,如图②所示:∵PC=20,PB=10,PC2=PB·PA,∴PA===40,∴AB=PA-PB=30,∵△PBC∽△PCA,∴==2,设BC=x,则AC=2x,在Rt△ABC中,x2+(2x)2=302,解得:x=6,即BC=6,∵点D是\s\up8(︵(︵)的中点,AB为⊙O的直径,∴∠AOD=90°,∵DE⊥AC,∴∠AEF=90°,∵∠ACB=90°,∴DE∥BC,∴∠DFO=∠ABC,∴△DOF∽△ACB,∴==,∴OF=OD=,即AF=,∵EF∥BC,∴==,∴EF=BC=
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
