第二十三章 旋转整理与复习
文档属性
| 名称 | 第二十三章 旋转整理与复习 | 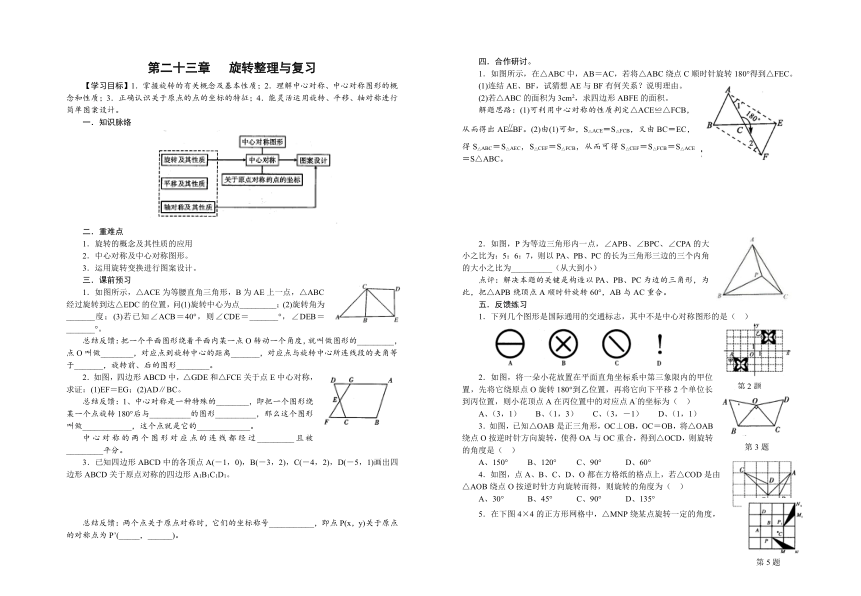 | |
| 格式 | zip | ||
| 文件大小 | 155.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-05 11:08:33 | ||
图片预览

文档简介
第二十三章 旋转整理与复习
【学习目标】1.掌握旋转的有关概念及基本性质;2.理解中心对称、中心对称图形的概念和性质;3.正确认识关于原点的点的坐标的特征;4.能灵活运用旋转、平移、轴对称进行简单图案设计。
一.知识脉络
二.重难点
1.旋转的概念及其性质的应用
2.中心对称及中心对称图形。
3.运用旋转变换进行图案设计。
三.课前预习
1.如图所示,△ACE为等腰直角三角形,B为AE上一点,△ABC经过旋转到达△EDC的位置,问(1)旋转中心为点_________;(2)旋转角为_______度;(3)若已知∠ACB=40°,则∠CDE=_______°,∠DEB=_______°。
总结反馈:把一个平面图形绕着平面内某一点O转动一个角度,就叫做图形的_________,点O叫做________,对应点到旋转中心的距离_______,对应点与旋转中心所连线段的夹角等于_______,旋转前、后的图形________。
2.如图,四边形ABCD中,△GDE和△FCE关于点E中心对称,求证:(1)EF=EG;(2)AD∥BC。
总结反馈:1、中心对称是一种特殊的________,即把一个图形绕某一个点旋转180°后与__________的图形__________,那么这个图形叫做____________,这个点就是它的_____________。
中心对称的两个图形对应点的连线都经过_________且被_________平分。
3.已知四边形ABCD中的各顶点A(-1,0),B(-3,2),C(-4,2),D(-5,1)画出四边形ABCD关于原点对称的四边形A1B1C1D1。
总结反馈:两个点关于原点对称时,它们的坐标称号___________,即点P(x,y)关于原点的对称点为P’(_____,______)。
四.合作研讨。
1.如图所示,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC。
(1)连结AE、BF,试猜想AE与BF有何关系?说明理由。
(2)若△ABC的面积为3cm2,求四边形ABFE的面积。
解题思路:(1)可利用中心对称的性质判定△ACE≌△FCB,从而得出AE//BF。(2)由(1)可知,S△ACE=S△FCB,又由BC=EC,得S△ABC=S△AEC,S△CEF=S△FCB,从而可得S△CEF=S△FCB=S△ACE=S△ABC。
2.如图,P为等边三角形内一点,∠APB、∠BPC、∠CPA的大小之比为:5:6:7,则以PA、PB、PC的长为三角形三边的三个内角的大小之比为__________(从大到小)
点评:解决本题的关键是构造以PA、PB、PC为边的三角形,为此,把△APB绕顶点A顺时针旋转60°,AB与AC重合。
五.反馈练习
1.下列几个图形是国际通用的交通标志,其中不是中心对称图形的是( )
2.如图,将一朵小花放置在平面直角坐标系中第三象限内的甲位置,先将它绕原点O旋转180°到乙位置,再将它向下平移2个单位长到丙位置,则小花顶点A在丙位置中的对应点A’的坐标为( )
A、(3,1) B、(1,3) C、(3,-1) D、(1,1)
3.如图,已知△OAB是正三角形,OC⊥OB,OC=OB,将△OAB绕点O按逆时针方向旋转,使得OA与OC重合,得到△OCD,则旋转的角度是( )
A、150° B、120° C、90° D、60°
4.如图,点A、B、C、D、O都在方格纸的格点上,若△COD是由△AOB绕点O按逆时针方向旋转而得,则旋转的角度为( )
A、30° B、45° C、90° D、135°
5.在下图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是( )
A、点A B、点B C、点C D、点D
6.△ABC在如图所示的平面直角坐标系中,将△ABC向右平移3个单位长度后得△A1B1C1,再将△A1B1C1绕点O旋转180°后得到△A2B2C2,则下列说法正确的是( )
A、A1的坐标为(3,1) B、=3
C、B2C=2 D、∠AC2O=45°
7.点P(1,2)关于原点的对称点P’的坐标为________
8.如图,E、F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE、BF,将△ABE绕正方形的中心按逆时针方向旋转得到△BCF,旋转角为α(0°<α<180°),则∠α=________
9.如图所示,四边形EFGH是由四边形ABCD经过旋转得到的。如果用有序数对(2,1)表示方格纸A点的位置,用(1,2)表示B点的位置,那么四边形ABCD旋转得到四边形EFGH时的旋转中心用有序数对表示是_______
10.如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1。
(1)线段OA1的长是________,∠AOB1的度数是________。
(2)连接AA1,求证:四边形OAA1B1是平行四边形。
(3)求四边形OAA1B1的面积。
11.在下面的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=6
(1)试作出△ABC以A为旋转中心、沿顺时针方向旋转90°后的图形△AB1C1。
(2)若点B的坐标为(-5,5),试建立合适的直角标系,并写出A、C两点的坐标。
12.如图,△ABD、△BCE都是等边三角形A、B、C在同一条直线上,AE交BD于F,CD交BE于G
(1)请用旋转的性质说明AE=CD
(2)试探究BG与BF之间的关系,并加以证明。
第2题
第3题
第4题
第5题
图9
图8
图6
【学习目标】1.掌握旋转的有关概念及基本性质;2.理解中心对称、中心对称图形的概念和性质;3.正确认识关于原点的点的坐标的特征;4.能灵活运用旋转、平移、轴对称进行简单图案设计。
一.知识脉络
二.重难点
1.旋转的概念及其性质的应用
2.中心对称及中心对称图形。
3.运用旋转变换进行图案设计。
三.课前预习
1.如图所示,△ACE为等腰直角三角形,B为AE上一点,△ABC经过旋转到达△EDC的位置,问(1)旋转中心为点_________;(2)旋转角为_______度;(3)若已知∠ACB=40°,则∠CDE=_______°,∠DEB=_______°。
总结反馈:把一个平面图形绕着平面内某一点O转动一个角度,就叫做图形的_________,点O叫做________,对应点到旋转中心的距离_______,对应点与旋转中心所连线段的夹角等于_______,旋转前、后的图形________。
2.如图,四边形ABCD中,△GDE和△FCE关于点E中心对称,求证:(1)EF=EG;(2)AD∥BC。
总结反馈:1、中心对称是一种特殊的________,即把一个图形绕某一个点旋转180°后与__________的图形__________,那么这个图形叫做____________,这个点就是它的_____________。
中心对称的两个图形对应点的连线都经过_________且被_________平分。
3.已知四边形ABCD中的各顶点A(-1,0),B(-3,2),C(-4,2),D(-5,1)画出四边形ABCD关于原点对称的四边形A1B1C1D1。
总结反馈:两个点关于原点对称时,它们的坐标称号___________,即点P(x,y)关于原点的对称点为P’(_____,______)。
四.合作研讨。
1.如图所示,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC。
(1)连结AE、BF,试猜想AE与BF有何关系?说明理由。
(2)若△ABC的面积为3cm2,求四边形ABFE的面积。
解题思路:(1)可利用中心对称的性质判定△ACE≌△FCB,从而得出AE//BF。(2)由(1)可知,S△ACE=S△FCB,又由BC=EC,得S△ABC=S△AEC,S△CEF=S△FCB,从而可得S△CEF=S△FCB=S△ACE=S△ABC。
2.如图,P为等边三角形内一点,∠APB、∠BPC、∠CPA的大小之比为:5:6:7,则以PA、PB、PC的长为三角形三边的三个内角的大小之比为__________(从大到小)
点评:解决本题的关键是构造以PA、PB、PC为边的三角形,为此,把△APB绕顶点A顺时针旋转60°,AB与AC重合。
五.反馈练习
1.下列几个图形是国际通用的交通标志,其中不是中心对称图形的是( )
2.如图,将一朵小花放置在平面直角坐标系中第三象限内的甲位置,先将它绕原点O旋转180°到乙位置,再将它向下平移2个单位长到丙位置,则小花顶点A在丙位置中的对应点A’的坐标为( )
A、(3,1) B、(1,3) C、(3,-1) D、(1,1)
3.如图,已知△OAB是正三角形,OC⊥OB,OC=OB,将△OAB绕点O按逆时针方向旋转,使得OA与OC重合,得到△OCD,则旋转的角度是( )
A、150° B、120° C、90° D、60°
4.如图,点A、B、C、D、O都在方格纸的格点上,若△COD是由△AOB绕点O按逆时针方向旋转而得,则旋转的角度为( )
A、30° B、45° C、90° D、135°
5.在下图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是( )
A、点A B、点B C、点C D、点D
6.△ABC在如图所示的平面直角坐标系中,将△ABC向右平移3个单位长度后得△A1B1C1,再将△A1B1C1绕点O旋转180°后得到△A2B2C2,则下列说法正确的是( )
A、A1的坐标为(3,1) B、=3
C、B2C=2 D、∠AC2O=45°
7.点P(1,2)关于原点的对称点P’的坐标为________
8.如图,E、F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE、BF,将△ABE绕正方形的中心按逆时针方向旋转得到△BCF,旋转角为α(0°<α<180°),则∠α=________
9.如图所示,四边形EFGH是由四边形ABCD经过旋转得到的。如果用有序数对(2,1)表示方格纸A点的位置,用(1,2)表示B点的位置,那么四边形ABCD旋转得到四边形EFGH时的旋转中心用有序数对表示是_______
10.如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1。
(1)线段OA1的长是________,∠AOB1的度数是________。
(2)连接AA1,求证:四边形OAA1B1是平行四边形。
(3)求四边形OAA1B1的面积。
11.在下面的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=6
(1)试作出△ABC以A为旋转中心、沿顺时针方向旋转90°后的图形△AB1C1。
(2)若点B的坐标为(-5,5),试建立合适的直角标系,并写出A、C两点的坐标。
12.如图,△ABD、△BCE都是等边三角形A、B、C在同一条直线上,AE交BD于F,CD交BE于G
(1)请用旋转的性质说明AE=CD
(2)试探究BG与BF之间的关系,并加以证明。
第2题
第3题
第4题
第5题
图9
图8
图6
同课章节目录
