苏科版七年级下册数学课件 9.2单项式乘多项式(19张)
文档属性
| 名称 | 苏科版七年级下册数学课件 9.2单项式乘多项式(19张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 734.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 00:00:00 | ||
图片预览

文档简介
单项式与多项式相乘,用单项式乘多项式的每一项,再把所得的积相加.
9.2 单项式乘多项式
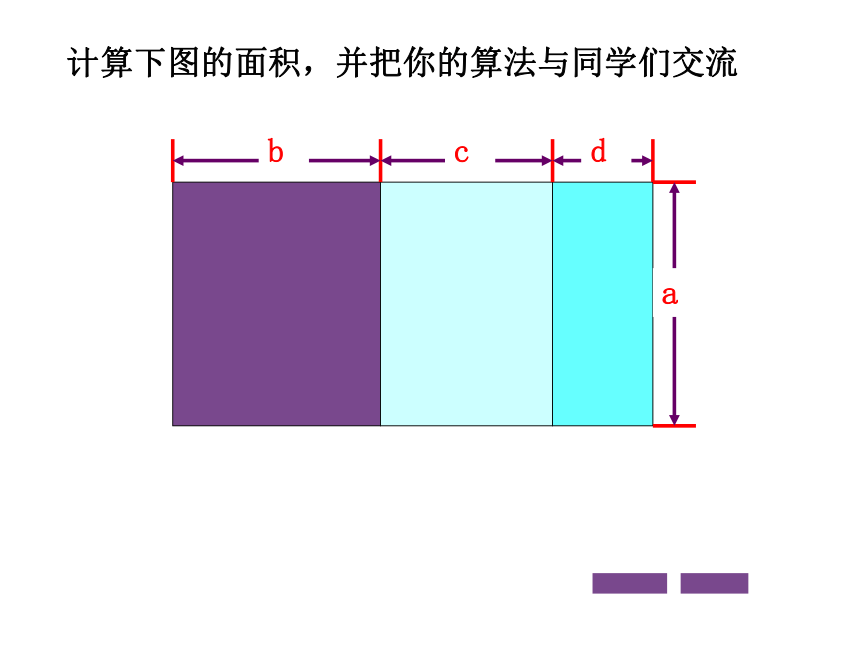
d
c
b
a
计算下图的面积,并把你的算法与同学们交流
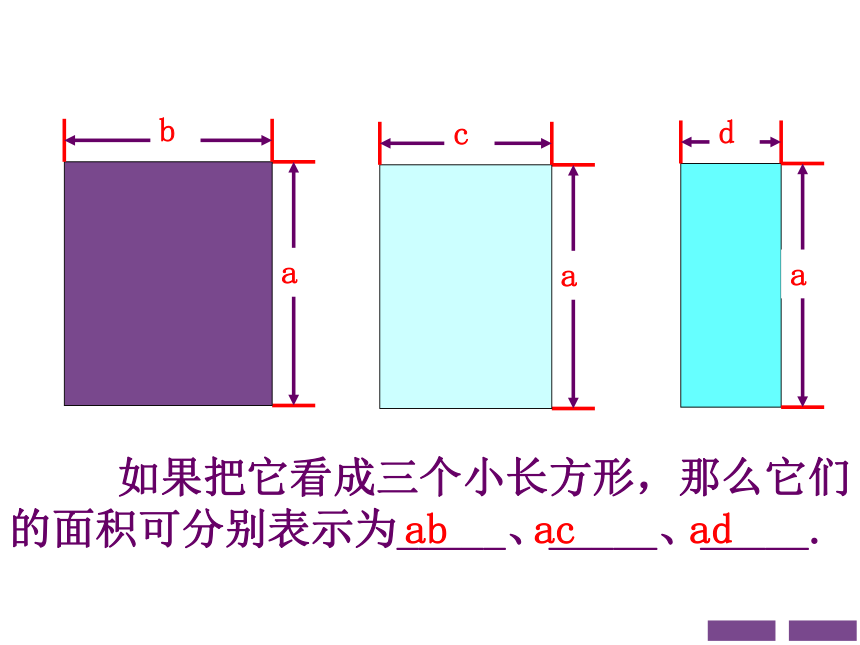
如果把它看成三个小长方形,那么它们的面积可分别表示为_____、_____、_____.
a
a
b
c
a
d
ab
ad
ac
d
c
b
a
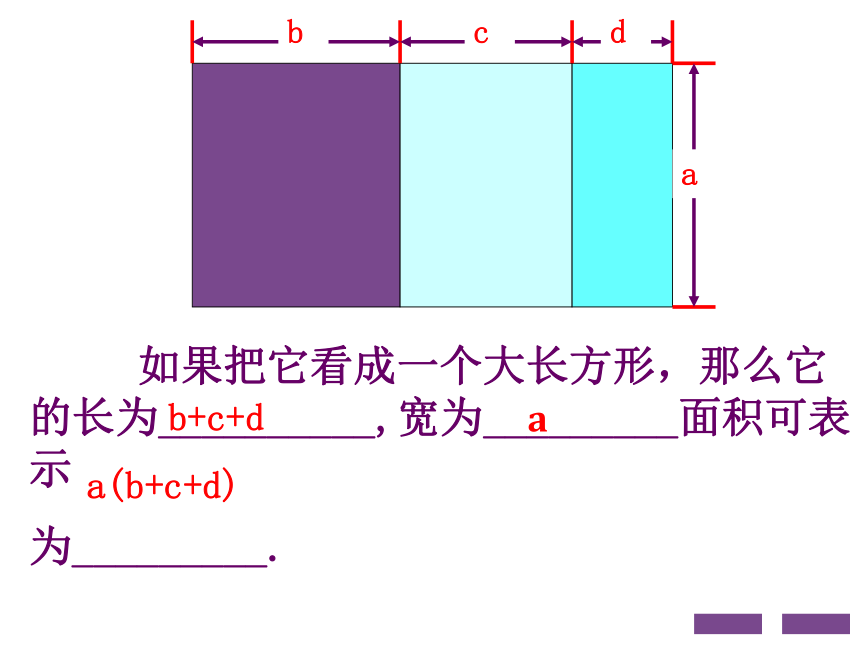
如果把它看成一个大长方形,那么它的长为__________,宽为_________面积可表示
为_________.
b+c+d
a(b+c+d)
a
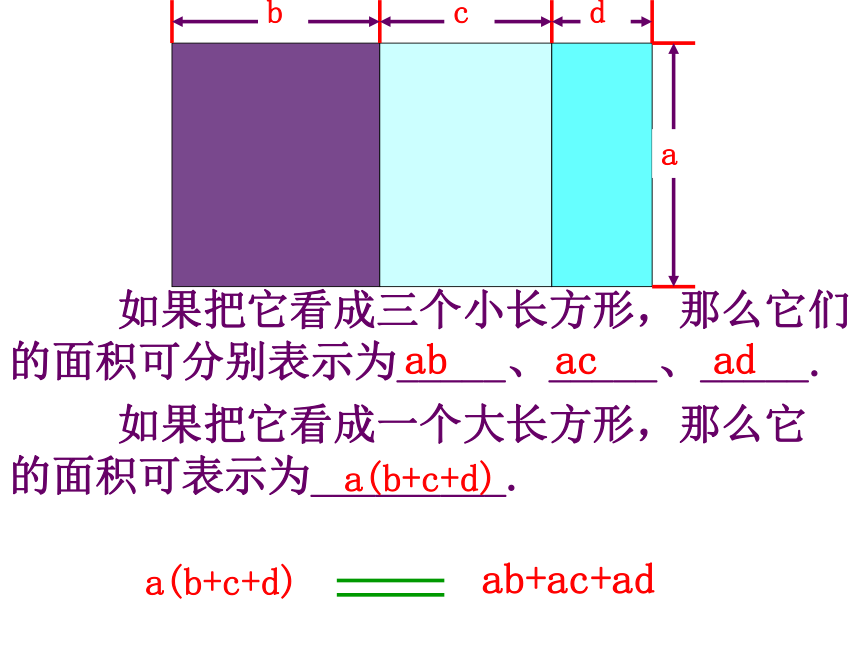
如果把它看成三个小长方形,那么它们的面积可分别表示为_____、_____、_____.
如果把它看成一个大长方形,那么它的面积可表示为_________.
d
c
b
a
ab
ad
ac
a(b+c+d)
ab+ac+ad
a(b+c+d)
ab+ac+ad
a(b+c+d)
a(b+c+d)
ac
+
ad
ab
+
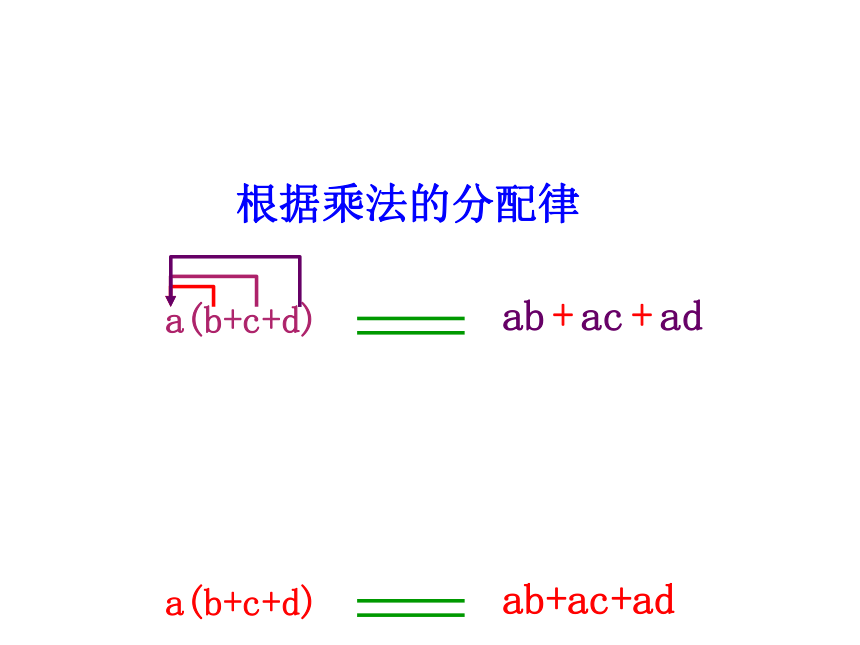
根据乘法的分配律
ab+ac+ad
a(b+c+d)
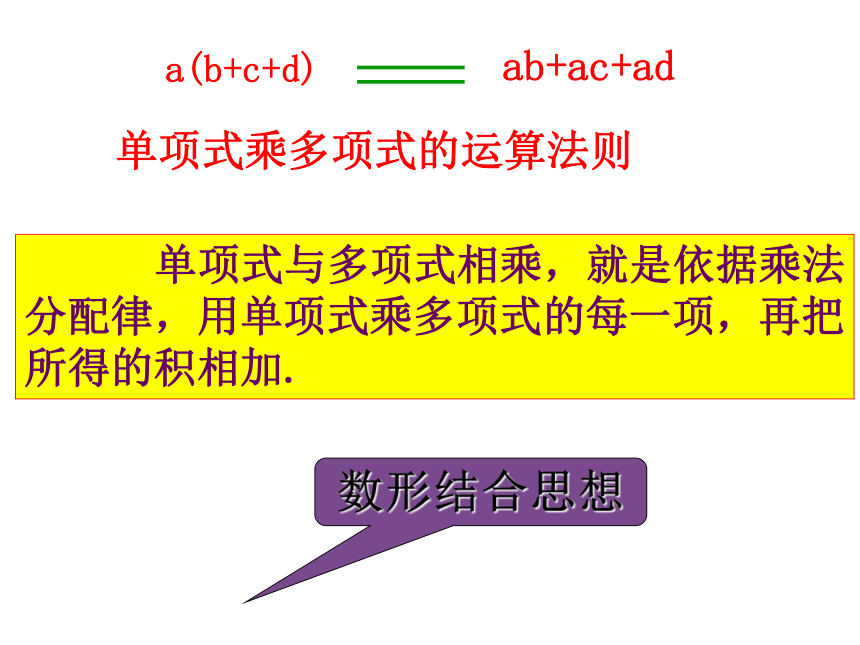
单项式与多项式相乘,就是依据乘法分配律,用单项式乘多项式的每一项,再把所得的积相加.
单项式乘多项式的运算法则
数形结合思想
单项式与多项式相乘,用单项式乘多项式的每一项,再把所得的积相加.
例1 计算:
⑴ (-3x2) ·(4x-3)
解:(-3x2) ·(4x-3)
=(-3x2) ·(4x)+(-3x2) ·(-3)
=-12x3+9x2
乘法分配律
单项式乘单项式运算法则
=-3x2?x+3x2?3
例1. 计算:
住宅用地
人民广场
商业用地
3a
3a+2b
2a-b
4a
例2:如图:一块长方形地用来建造住宅、广场、商厦,求这块地的面积.
如图,求梯形的面积
例3.先化简,再求值:
练习:
先化简,再求值:
其中
,
.
思维拓展
要使
项,
的结果中不含
则a等于
?
小结与回顾
例4、已知:xy2=-6,求
-xy(x3y7-3x2y5-y)的值.
2.一家住房的结构如图,这家房子的主人打算把卧室以外的部分铺上地砖,至少需要多少平方米的地砖?如果某种地砖的价格是a元/m2,那么购买所需的地砖至少需要多少元?
卫生间
卧 室
厨 房
客 厅
y
2y
4x
4y
2x
x
9.2 单项式乘多项式
d
c
b
a
计算下图的面积,并把你的算法与同学们交流
如果把它看成三个小长方形,那么它们的面积可分别表示为_____、_____、_____.
a
a
b
c
a
d
ab
ad
ac
d
c
b
a
如果把它看成一个大长方形,那么它的长为__________,宽为_________面积可表示
为_________.
b+c+d
a(b+c+d)
a
如果把它看成三个小长方形,那么它们的面积可分别表示为_____、_____、_____.
如果把它看成一个大长方形,那么它的面积可表示为_________.
d
c
b
a
ab
ad
ac
a(b+c+d)
ab+ac+ad
a(b+c+d)
ab+ac+ad
a(b+c+d)
a(b+c+d)
ac
+
ad
ab
+
根据乘法的分配律
ab+ac+ad
a(b+c+d)
单项式与多项式相乘,就是依据乘法分配律,用单项式乘多项式的每一项,再把所得的积相加.
单项式乘多项式的运算法则
数形结合思想
单项式与多项式相乘,用单项式乘多项式的每一项,再把所得的积相加.
例1 计算:
⑴ (-3x2) ·(4x-3)
解:(-3x2) ·(4x-3)
=(-3x2) ·(4x)+(-3x2) ·(-3)
=-12x3+9x2
乘法分配律
单项式乘单项式运算法则
=-3x2?x+3x2?3
例1. 计算:
住宅用地
人民广场
商业用地
3a
3a+2b
2a-b
4a
例2:如图:一块长方形地用来建造住宅、广场、商厦,求这块地的面积.
如图,求梯形的面积
例3.先化简,再求值:
练习:
先化简,再求值:
其中
,
.
思维拓展
要使
项,
的结果中不含
则a等于
?
小结与回顾
例4、已知:xy2=-6,求
-xy(x3y7-3x2y5-y)的值.
2.一家住房的结构如图,这家房子的主人打算把卧室以外的部分铺上地砖,至少需要多少平方米的地砖?如果某种地砖的价格是a元/m2,那么购买所需的地砖至少需要多少元?
卫生间
卧 室
厨 房
客 厅
y
2y
4x
4y
2x
x
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
