苏科版七年级下册数学课件 9.4乘法公式(18张)
文档属性
| 名称 | 苏科版七年级下册数学课件 9.4乘法公式(18张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 589.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 00:00:00 | ||
图片预览






文档简介
9.4乘法公式(二)
创设情境
如图:边长为b的小正方形放置在边长为a的大正方形纸片上,你能计算出未盖住部分的面积吗?
a
a
b
b
如果把它们看成2个梯形,那么它们的面积可表示为______________
如果把它们看成是1个大正方形与1个小正方形的面积之差,那么可表示为___________
(a+b)(a-b)
a2-b2
(a+b)(a-b)
+
ab
a2
ab
-
a2-b2
(a+b)(a-b)
b2
-
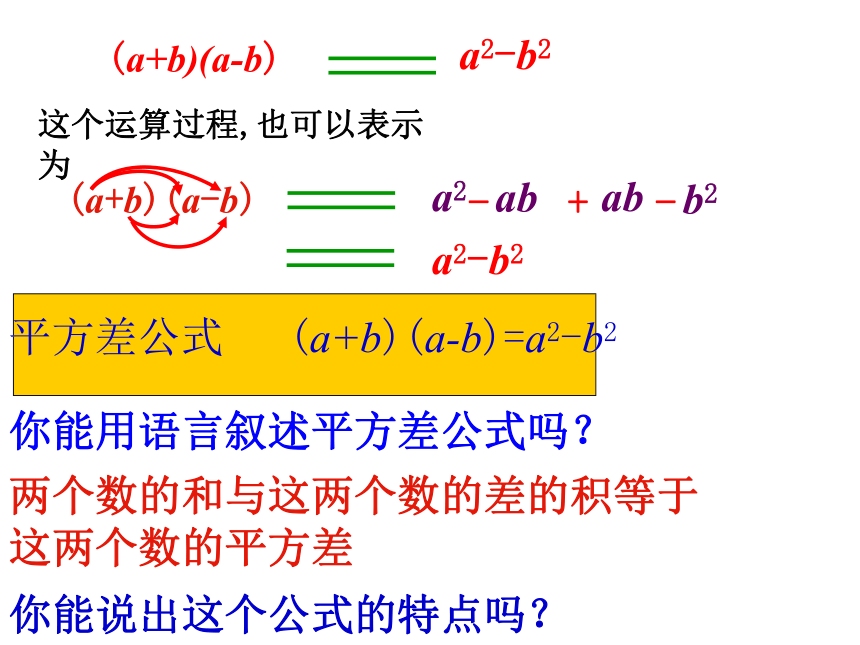
这个运算过程,也可以表示为
a2-b2
平方差公式 (a+b)(a-b)=a2-b2
你能说出这个公式的特点吗?
你能用语言叙述平方差公式吗?
两个数的和与这两个数的差的积等于这两个数的平方差
特点:
公式的左边:
两个二项式的积,其中有一项(a)完全相同,另一项(b和-b)互为相反数;
公式的右边:
这两项的平方差。
两个数的和与这两个数的差的积,等于这两个数的平方差。
平方差公式:
比一比、赛一赛,看谁算得快!
试一试:
例:用平方差公式计算:
辨一辨:
下列能否用平方差公式进行计算:
能
能
不能
不能
能
用平方差公式计算:
练一练:
说出一个两项式
说出另一个两项式,使它们两个相乘符合平方差公式
玩一玩:
报出结果
填一填:
例1 用平方差公式计算:
(5x+y)(5x-y)
想一想
(2)(5x+y)(y-5x)
(3)(-5x+y)(-5x-y)
(4)(-5x+y)(5x-y)
例2 用简便方法计算:102×98
赛一赛:
小刚家草莓地的面积:
10.2×9.8=
(10+0.2) ×(10-0.2)
= 102-0.22
=100-0.04
=99.96
挑战自我:
(1)49×51
解:原式=(50-1) ×(50+1)
=502-12
=2500-1
=2499
动动手、动动脑:
小刚家刚分了一块边长为a的正方形地,缺了一块,这块正好是边长为b的小正方形,如图,你能帮他爸爸用不同的方法表示出这块地的面积吗?
b
a
a
b
1
2
3
5
4
拓一拓、展一展:
1.计算 20042-2003×2005;
2.请你利用平方差公式求出(2+1)(22+1)(24+1)(28+1)……(264+1)的值.
小结与回顾
(1)掌握平方差公式的特点
平方差公式的结果是两项
(2) 能利用平方差公式进行计算
创设情境
如图:边长为b的小正方形放置在边长为a的大正方形纸片上,你能计算出未盖住部分的面积吗?
a
a
b
b
如果把它们看成2个梯形,那么它们的面积可表示为______________
如果把它们看成是1个大正方形与1个小正方形的面积之差,那么可表示为___________
(a+b)(a-b)
a2-b2
(a+b)(a-b)
+
ab
a2
ab
-
a2-b2
(a+b)(a-b)
b2
-
这个运算过程,也可以表示为
a2-b2
平方差公式 (a+b)(a-b)=a2-b2
你能说出这个公式的特点吗?
你能用语言叙述平方差公式吗?
两个数的和与这两个数的差的积等于这两个数的平方差
特点:
公式的左边:
两个二项式的积,其中有一项(a)完全相同,另一项(b和-b)互为相反数;
公式的右边:
这两项的平方差。
两个数的和与这两个数的差的积,等于这两个数的平方差。
平方差公式:
比一比、赛一赛,看谁算得快!
试一试:
例:用平方差公式计算:
辨一辨:
下列能否用平方差公式进行计算:
能
能
不能
不能
能
用平方差公式计算:
练一练:
说出一个两项式
说出另一个两项式,使它们两个相乘符合平方差公式
玩一玩:
报出结果
填一填:
例1 用平方差公式计算:
(5x+y)(5x-y)
想一想
(2)(5x+y)(y-5x)
(3)(-5x+y)(-5x-y)
(4)(-5x+y)(5x-y)
例2 用简便方法计算:102×98
赛一赛:
小刚家草莓地的面积:
10.2×9.8=
(10+0.2) ×(10-0.2)
= 102-0.22
=100-0.04
=99.96
挑战自我:
(1)49×51
解:原式=(50-1) ×(50+1)
=502-12
=2500-1
=2499
动动手、动动脑:
小刚家刚分了一块边长为a的正方形地,缺了一块,这块正好是边长为b的小正方形,如图,你能帮他爸爸用不同的方法表示出这块地的面积吗?
b
a
a
b
1
2
3
5
4
拓一拓、展一展:
1.计算 20042-2003×2005;
2.请你利用平方差公式求出(2+1)(22+1)(24+1)(28+1)……(264+1)的值.
小结与回顾
(1)掌握平方差公式的特点
平方差公式的结果是两项
(2) 能利用平方差公式进行计算
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
