苏科版七年级下册数学课件 9.1单项式乘单项式(29张)
文档属性
| 名称 | 苏科版七年级下册数学课件 9.1单项式乘单项式(29张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 21:35:09 | ||
图片预览








文档简介
1下列整式中哪些是单项式?哪些是多项式?
知识复习:
2、利用乘法的交换律,结合律计算:
6×4×13×25
解:原式= (6 ×13) ×(4×25)
=78 ×100
=7800
知识复习:
3、前面学习了哪三种幂的运算?
运算方法分别是什么?
公式的逆运算你会吗?
知识复习:
1、同底数幂相乘,底数不变,指数相加。
一般形式:
2、幂的乘方,底数不变,指数相乘
一般形式:
( n ,m 为正整数)
(m,n为正整数)
3、 积的乘方等于各因数乘方的积
一般形式:
(n为正整数)
知识复习:
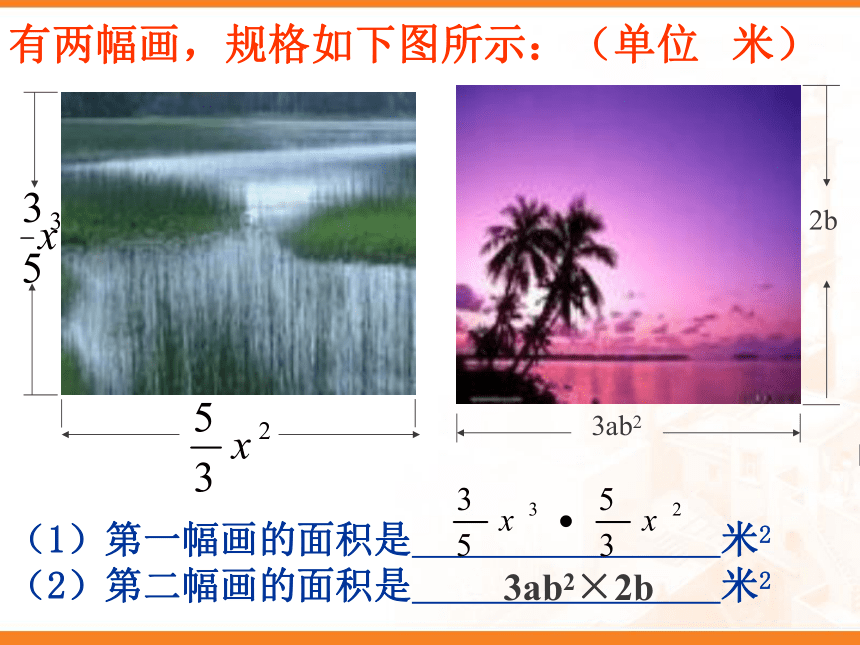
有两幅画,规格如下图所示:(单位 米)
(1)第一幅画的面积是 米2
(2)第二幅画的面积是 米2
3ab2
2b
3ab2×2b
乘法交换律(ab=ba)
乘法结合律(ab)c=a(bc)
注意:这里实质是
同底数幂的乘法的应用
5×103
1.2×102
( )
( )
×
= ( 5× ) ×( ×102)
=6×105
1.2
103
变式1:
5___
·
1.2___
a4
a3
=(___×____)(___·____)=____
5
a4
a3
6a7
变式2:
5a4
·
(-1.2a3b2)
=[__×(-1.2)] ●(a4a3)__
5
b2
=-6a7b2
1.2
从以上这些式子中你能发现进行单项式与单项式相乘的运算规律吗?
1、系数相乘
2、同底数的幂相乘
3、只在一个单项式里含有的字母,
连同它的指数作为积的一个因式。
有理数的乘法
单项式的乘法法则包括以下三部分:
(1)积的系数等于各因式系数的积;
(2)相同字母相乘;
(3)只在一个单项式里含有的字母,
要连同它的指数写在积里.
(注意 不要把这个因式丢掉)
(同底数幂的乘法)
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
单项式的乘法法则
同 学 们,你 们 知 道 我 们 的教 室 有 多 大 吗? 小 明 想 要 估 算 它 的 面 积,你 能 帮 助 他 解 决 问 题 吗?
问题: (13a) ? (9a)结果可以表达的更简单些吗?试一试?
小明采用步长测量教室的面积,测量长时走了13步,测量宽时走了9步,如果小明的步长用a米表示, 你能用含a的代数式表示教室的面积吗?
若小明的步长为0.7米,那么教室面积约是多少?
解:(13a) ? (9a)
(13× 0.7) ? (9 × 0.7)
= 9.1 × 6.3
=57.33(m2)
(根据什么?)
(乘法交换律和结合律)
=(13 ×9 )×(a ? a)
=117a2
=57.33 (m2)
117×0.72
例题2:卫星绕地球运动的速度(即第一宇宙速度)约为7.9× 米/秒,则卫星运行3× 秒所走的路程约是多少米?
解: 7.9× × 3×
=23.7 ×
=2.37 ×
答:卫星绕地球运行3× 秒走过的路程约是2.37 × 米。
结果要用科学记数法表示
研究课题:
下面的三个式子可以表达的更简单吗?你的理由是什么? 分组研究!
(1)
(2)
(3)
解:原式
各因数系数结合成一组
相同的字母结合成一组
系数的积作为积的系数
对于相同的字母,用它们的指数和作为积里这个字母的指数
对于只有一个单项式里含有的字母,连同它的指数作为积的一个因式
(3)
(系数×系数)
(同底数幂相乘)
×单独的幂
计算:
解:原式=
单项式与单项式相乘的法则
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,其余字母连同它的指数不变,作为积的因式。
例1:计算
解:原式
解:原式
解:原式
例3 计算
(-2a2)3 ·(-3a3)2
观察一下,例3比例2多了什么运算?
例2 计算
注意:
(1)先做乘方,再做单项式相乘。
(2)系数相乘不要漏掉负号
例3 计算:
(1)(2?104)(5 ? 103) ? 107
解(1)原式=(2 ?5)(104 ×103× 107 )
=10?1014
=1015
(2) (4 ? 105) ·(5 ? 106) ·(3?104)
(2)原式=(4?5 ? 3)(105 ? 106 ? 104)
=60?1015
=6?1016
这里有三个单项式
相乘,还可以利用
上面的法则吗?
数 学 活 动 室
计算:
解:原式
单项式与单项式相乘的运算法则
B
×
×
×
×
(1)4a2 ?2a4 = 8a8 ( )
(2)6a3 ?5a2=11a5 ( )
(3)(-7a)?(-3a3) =-21a4 ( )
(4)3a2b ?4a3=12a5 ( )
系数相乘
同底数幂的乘法,底数不变,指数相加
只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏.
求系数的积,应注意符号
求系数的积,应注意符号;
相同字母因式相乘,是同底数幂的乘法,底数不变,指数相加;
只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏;
单项式乘以单项式的结果仍然是一个单项式,结果要把系数写在字母因式的前面;
单项式乘法的法则对于三个以上的单项式相乘同样适用。
(2)
2
细心填一填:
(1) ( )
3
计算:
1、
2、
3x2y ? (-2xy3);
(-5a2b3)? (-4b2c)
解:(1)3x2y ? (-2xy3)
= [3 ? (-2)] ? (x2 ? x)? (y ? y3)
= -6x3y4
(2)(-5a2b3)? (-4b2c)
=[(-5)? (-4)] ? a2? (b3 ? b2)? c
=20a2b5c
2.计算:
(1)(-2x2)·(-3x2y3)2=________;
-18x6y6
(2)(-2xy2)2·(-3xyn)·(-x2z)=________.
12x5y4+nz
(1)原式= (-2x2)·(9 x4y6)
(2)原式=(4x2y4) ·(-3xyn)·(-x2z)
-9x3y2
a2bXn+2
a6nb6n
2?1012
计算:
提高题:计算:
班级论坛
讨 论
可是看作是边长为 正方形面积, 又怎么理解呢?
可以看作是高为 ,底面长和宽分别为 的长方体体积!
你能说出 , 以及 的几何意义吗
请 你 算 一 算:
单项式与单项式相乘
同底数幂相乘
只在一个单项式中出现的字母,则连同它的指数一起作为积的一个因式
系数乘以系数
知识复习:
2、利用乘法的交换律,结合律计算:
6×4×13×25
解:原式= (6 ×13) ×(4×25)
=78 ×100
=7800
知识复习:
3、前面学习了哪三种幂的运算?
运算方法分别是什么?
公式的逆运算你会吗?
知识复习:
1、同底数幂相乘,底数不变,指数相加。
一般形式:
2、幂的乘方,底数不变,指数相乘
一般形式:
( n ,m 为正整数)
(m,n为正整数)
3、 积的乘方等于各因数乘方的积
一般形式:
(n为正整数)
知识复习:
有两幅画,规格如下图所示:(单位 米)
(1)第一幅画的面积是 米2
(2)第二幅画的面积是 米2
3ab2
2b
3ab2×2b
乘法交换律(ab=ba)
乘法结合律(ab)c=a(bc)
注意:这里实质是
同底数幂的乘法的应用
5×103
1.2×102
( )
( )
×
= ( 5× ) ×( ×102)
=6×105
1.2
103
变式1:
5___
·
1.2___
a4
a3
=(___×____)(___·____)=____
5
a4
a3
6a7
变式2:
5a4
·
(-1.2a3b2)
=[__×(-1.2)] ●(a4a3)__
5
b2
=-6a7b2
1.2
从以上这些式子中你能发现进行单项式与单项式相乘的运算规律吗?
1、系数相乘
2、同底数的幂相乘
3、只在一个单项式里含有的字母,
连同它的指数作为积的一个因式。
有理数的乘法
单项式的乘法法则包括以下三部分:
(1)积的系数等于各因式系数的积;
(2)相同字母相乘;
(3)只在一个单项式里含有的字母,
要连同它的指数写在积里.
(注意 不要把这个因式丢掉)
(同底数幂的乘法)
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
单项式的乘法法则
同 学 们,你 们 知 道 我 们 的教 室 有 多 大 吗? 小 明 想 要 估 算 它 的 面 积,你 能 帮 助 他 解 决 问 题 吗?
问题: (13a) ? (9a)结果可以表达的更简单些吗?试一试?
小明采用步长测量教室的面积,测量长时走了13步,测量宽时走了9步,如果小明的步长用a米表示, 你能用含a的代数式表示教室的面积吗?
若小明的步长为0.7米,那么教室面积约是多少?
解:(13a) ? (9a)
(13× 0.7) ? (9 × 0.7)
= 9.1 × 6.3
=57.33(m2)
(根据什么?)
(乘法交换律和结合律)
=(13 ×9 )×(a ? a)
=117a2
=57.33 (m2)
117×0.72
例题2:卫星绕地球运动的速度(即第一宇宙速度)约为7.9× 米/秒,则卫星运行3× 秒所走的路程约是多少米?
解: 7.9× × 3×
=23.7 ×
=2.37 ×
答:卫星绕地球运行3× 秒走过的路程约是2.37 × 米。
结果要用科学记数法表示
研究课题:
下面的三个式子可以表达的更简单吗?你的理由是什么? 分组研究!
(1)
(2)
(3)
解:原式
各因数系数结合成一组
相同的字母结合成一组
系数的积作为积的系数
对于相同的字母,用它们的指数和作为积里这个字母的指数
对于只有一个单项式里含有的字母,连同它的指数作为积的一个因式
(3)
(系数×系数)
(同底数幂相乘)
×单独的幂
计算:
解:原式=
单项式与单项式相乘的法则
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,其余字母连同它的指数不变,作为积的因式。
例1:计算
解:原式
解:原式
解:原式
例3 计算
(-2a2)3 ·(-3a3)2
观察一下,例3比例2多了什么运算?
例2 计算
注意:
(1)先做乘方,再做单项式相乘。
(2)系数相乘不要漏掉负号
例3 计算:
(1)(2?104)(5 ? 103) ? 107
解(1)原式=(2 ?5)(104 ×103× 107 )
=10?1014
=1015
(2) (4 ? 105) ·(5 ? 106) ·(3?104)
(2)原式=(4?5 ? 3)(105 ? 106 ? 104)
=60?1015
=6?1016
这里有三个单项式
相乘,还可以利用
上面的法则吗?
数 学 活 动 室
计算:
解:原式
单项式与单项式相乘的运算法则
B
×
×
×
×
(1)4a2 ?2a4 = 8a8 ( )
(2)6a3 ?5a2=11a5 ( )
(3)(-7a)?(-3a3) =-21a4 ( )
(4)3a2b ?4a3=12a5 ( )
系数相乘
同底数幂的乘法,底数不变,指数相加
只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏.
求系数的积,应注意符号
求系数的积,应注意符号;
相同字母因式相乘,是同底数幂的乘法,底数不变,指数相加;
只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏;
单项式乘以单项式的结果仍然是一个单项式,结果要把系数写在字母因式的前面;
单项式乘法的法则对于三个以上的单项式相乘同样适用。
(2)
2
细心填一填:
(1) ( )
3
计算:
1、
2、
3x2y ? (-2xy3);
(-5a2b3)? (-4b2c)
解:(1)3x2y ? (-2xy3)
= [3 ? (-2)] ? (x2 ? x)? (y ? y3)
= -6x3y4
(2)(-5a2b3)? (-4b2c)
=[(-5)? (-4)] ? a2? (b3 ? b2)? c
=20a2b5c
2.计算:
(1)(-2x2)·(-3x2y3)2=________;
-18x6y6
(2)(-2xy2)2·(-3xyn)·(-x2z)=________.
12x5y4+nz
(1)原式= (-2x2)·(9 x4y6)
(2)原式=(4x2y4) ·(-3xyn)·(-x2z)
-9x3y2
a2bXn+2
a6nb6n
2?1012
计算:
提高题:计算:
班级论坛
讨 论
可是看作是边长为 正方形面积, 又怎么理解呢?
可以看作是高为 ,底面长和宽分别为 的长方体体积!
你能说出 , 以及 的几何意义吗
请 你 算 一 算:
单项式与单项式相乘
同底数幂相乘
只在一个单项式中出现的字母,则连同它的指数一起作为积的一个因式
系数乘以系数
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
