鲁教版(五四制)八年级下册数学 6.1.2菱形的判定 课件(26张)
文档属性
| 名称 | 鲁教版(五四制)八年级下册数学 6.1.2菱形的判定 课件(26张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 771.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-28 00:00:00 | ||
图片预览




文档简介
6.1 菱形的性质与判定(2)
2cm
1cm
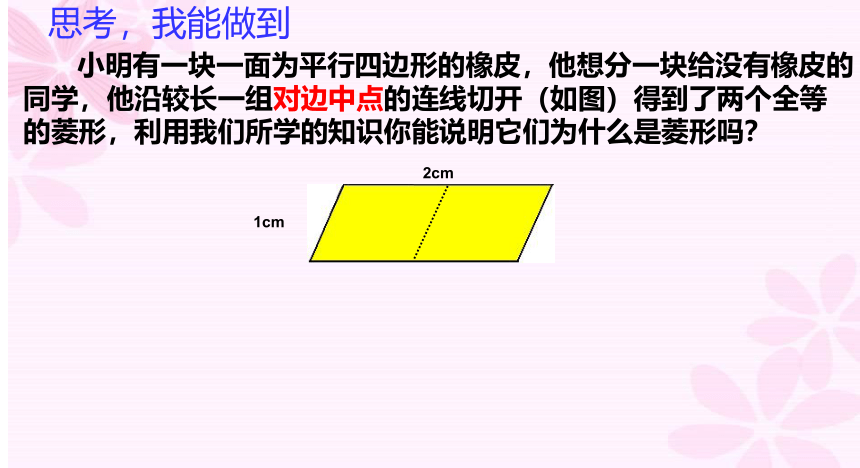
小明有一块一面为平行四边形的橡皮,他想分一块给没有橡皮的同学,他沿较长一组对边中点的连线切开(如图)得到了两个全等的菱形,利用我们所学的知识你能说明它们为什么是菱形吗?
思考,我能做到
1cm
1cm
1cm
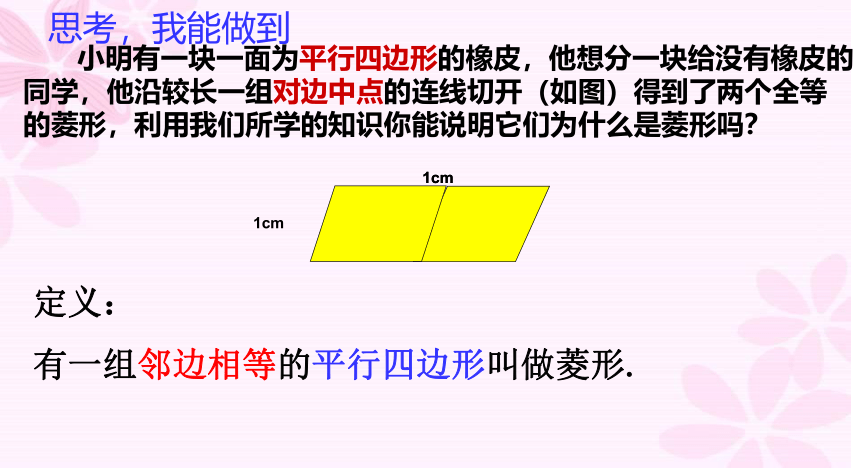
定义:
有一组邻边相等的平行四边形叫做菱形.
思考,我能做到
小明有一块一面为平行四边形的橡皮,他想分一块给没有橡皮的同学,他沿较长一组对边中点的连线切开(如图)得到了两个全等的菱形,利用我们所学的知识你能说明它们为什么是菱形吗?
利用手中的材料制作菱形
(1)两根木条(钉子在两根木条的中点处)、图钉、皮筋
(2)火柴若干(火柴不许折断)
合作,我们共赢
猜想:
对角线互相垂直的平行四边形是菱形
猜想:
有四条边相等的四边形是菱形
合作,我们共赢
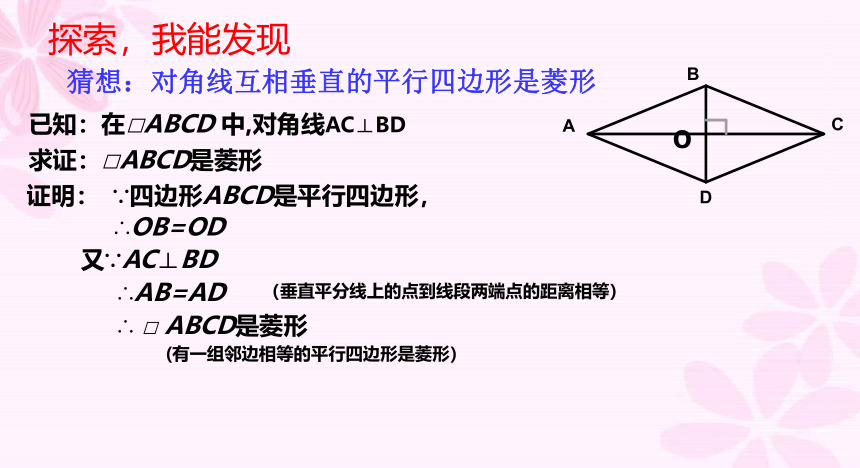
已知:在□ABCD 中,对角线AC⊥BD
求证:□ABCD是菱形
O
猜想:对角线互相垂直的平行四边形是菱形
探索,我能发现
证明:
∵四边形ABCD是平行四边形,
∴OB=OD
又∵AC⊥BD
∴ □ ABCD是菱形
∴AB=AD
(有一组邻边相等的平行四边形是菱形)
(垂直平分线上的点到线段两端点的距离相等)
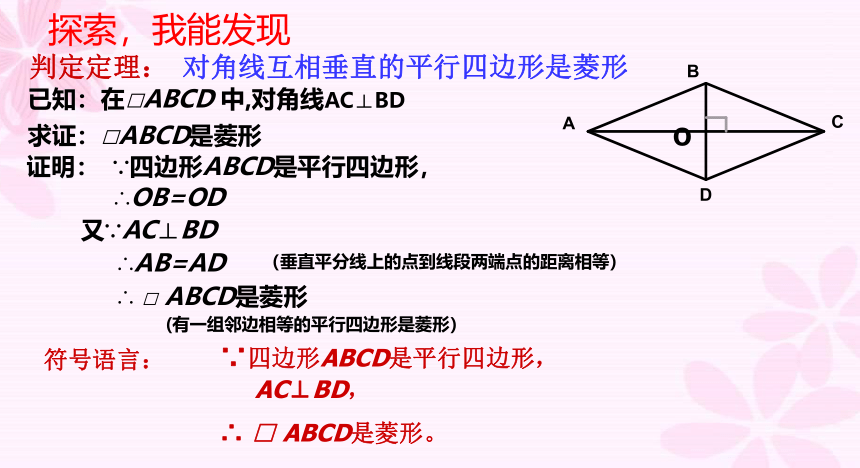
已知:在□ABCD 中,对角线AC⊥BD
求证:□ABCD是菱形
O
对角线互相垂直的平行四边形是菱形
探索,我能发现
判定定理:
∵四边形ABCD是平行四边形,
AC⊥BD,
∴ □ ABCD是菱形。
符号语言:
证明:
∵四边形ABCD是平行四边形,
∴OB=OD
又∵AC⊥BD
∴ □ ABCD是菱形
∴AB=AD
(有一组邻边相等的平行四边形是菱形)
(垂直平分线上的点到线段两端点的距离相等)
已知:在四边形ABCD中,
AB=BC=CD=DA
求证:四边形ABCD是菱形
∴四边形ABCD是平行四边形
证明:
∴四边形ABCD是菱形
(有一组邻边相等的平行四边形叫做菱形)
∵AD=BC AB=CD
又∵AB=AD
A
B
C
D
猜想:有四条边相等的四边形是菱形
探索,我能发现
已知:在四边形ABCD中,
AB=BC=CD=DA
求证:四边形ABCD是菱形
∴四边形ABCD是平行四边形
证明:
∴四边形ABCD是菱形
(有一组邻边相等的平行四边形叫做菱形)
∵AD=BC AB=CD
又∵AB=AD
A
B
C
D
有四条边相等的四边形是菱形
探索,我能发现
判定定理:
符号语言:
∵ AB=BC=CD=DA
∴四边形ABCD是菱形
一组邻边相等
对角线互相垂直
四条边相等
四边形
平行四边形
菱形
菱形的判定方法:
归纳,使我飞跃
1.________的平行四边形是菱形.
2.________的平行四边形是菱形.
3.________的四边形是菱形.
例3 如图,在□ ABCD中,对角线AC与BD
相交于点O,AB= ,AO=2,BO=1.
求证: □ ABCD是菱形
A
B
C
D
O
∴ □ ABCD是菱形.
证明:
∴
∴△OAB是直角三角形,∠ AOB是直角
∵AB= , AO=2,BO=1.
动手,我能提高
在△OAB中
∴ AC⊥BD
请用手中的尺规作一个边长为2厘米的菱形
动手,我能提高
练习,我能提升
1.将一张矩形纸对折再对折(如图),然后沿着图中的虚线剪下,得到①、②两部分,将①展开后得到的平面图形是( )
A.矩形 B.三角形 C.梯形 D.菱形
练习,我能提升
2.把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
E
F
收获和质疑
一组邻边相等
对角线互相垂直
四条边相等
四边形
平行四边形
菱形
菱形的判定方法:
猜想:
对角线互相垂直的平行四边形是菱形
猜想:
有四条边相等的四边形是菱形
已知:在□ABCD 中,对角线AC⊥BD
求证:□ABCD是菱形
O
猜想:对角线互相垂直的平行四边形是菱形
探索,我能发现
证明:
∵四边形ABCD是平行四边形,
∴OB=OD
又∵AC⊥BD
∴ □ ABCD是菱形
∴AB=AD
(有一组邻边相等的平行四边形是菱形)
(垂直平分线上的点到线段两端点的距离相等)
已知:在□ABCD 中,对角线AC⊥BD
求证:□ABCD是菱形
O
对角线互相垂直的平行四边形是菱形
探索,我能发现
判定定理:
∵四边形ABCD是平行四边形,
AC⊥BD,
∴ □ ABCD是菱形。
符号语言:
证明:
∵四边形ABCD是平行四边形,
∴OB=OD
又∵AC⊥BD
∴ □ ABCD是菱形
∴AB=AD
(有一组邻边相等的平行四边形是菱形)
(垂直平分线上的点到线段两端点的距离相等)
已知:在四边形ABCD中,
AB=BC=CD=DA
求证:四边形ABCD是菱形
∴四边形ABCD是平行四边形
证明:
∴四边形ABCD是菱形
(有一组邻边相等的平行四边形叫做菱形)
∵AD=BC AB=CD
又∵AB=AD
A
B
C
D
猜想:有四条边相等的四边形是菱形
探索,我能发现
已知:在四边形ABCD中,
AB=BC=CD=DA
求证:四边形ABCD是菱形
∴四边形ABCD是平行四边形
证明:
∴四边形ABCD是菱形
(有一组邻边相等的平行四边形叫做菱形)
∵AD=BC AB=CD
又∵AB=AD
A
B
C
D
有四条边相等的四边形是菱形
探索,我能发现
判定定理:
符号语言:
∵ AB=BC=CD=DA
∴四边形ABCD是菱形
一组邻边相等
对角线互相垂直
四条边相等
四边形
平行四边形
菱形
菱形的判定方法:
归纳,使我飞跃
1.________的平行四边形是菱形.
2.________的平行四边形是菱形.
3.________的四边形是菱形.
例3 如图,在□ ABCD中,对角线AC与BD
相交于点O,AB= ,AO=2,BO=1.
求证: □ ABCD是菱形
A
B
C
D
O
∴ □ ABCD是菱形.
证明:
∴
∴△OAB是直角三角形,∠ AOB是直角
∵AB= , AO=2,BO=1.
动手,我能提高
在△OAB中
∴ AC⊥BD
请用手中的尺规作一个边长为2厘米的菱形
动手,我能提高
练习,我能提升
1.将一张矩形纸对折再对折(如图),然后沿着图中的虚线剪下,得到①、②两部分,将①展开后得到的平面图形是( )
A.矩形 B.三角形 C.梯形 D.菱形
练习,我能提升
2.把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
E
F
2cm
1cm
小明有一块一面为平行四边形的橡皮,他想分一块给没有橡皮的同学,他沿较长一组对边中点的连线切开(如图)得到了两个全等的菱形,利用我们所学的知识你能说明它们为什么是菱形吗?
思考,我能做到
1cm
1cm
1cm
定义:
有一组邻边相等的平行四边形叫做菱形.
思考,我能做到
小明有一块一面为平行四边形的橡皮,他想分一块给没有橡皮的同学,他沿较长一组对边中点的连线切开(如图)得到了两个全等的菱形,利用我们所学的知识你能说明它们为什么是菱形吗?
利用手中的材料制作菱形
(1)两根木条(钉子在两根木条的中点处)、图钉、皮筋
(2)火柴若干(火柴不许折断)
合作,我们共赢
猜想:
对角线互相垂直的平行四边形是菱形
猜想:
有四条边相等的四边形是菱形
合作,我们共赢
已知:在□ABCD 中,对角线AC⊥BD
求证:□ABCD是菱形
O
猜想:对角线互相垂直的平行四边形是菱形
探索,我能发现
证明:
∵四边形ABCD是平行四边形,
∴OB=OD
又∵AC⊥BD
∴ □ ABCD是菱形
∴AB=AD
(有一组邻边相等的平行四边形是菱形)
(垂直平分线上的点到线段两端点的距离相等)
已知:在□ABCD 中,对角线AC⊥BD
求证:□ABCD是菱形
O
对角线互相垂直的平行四边形是菱形
探索,我能发现
判定定理:
∵四边形ABCD是平行四边形,
AC⊥BD,
∴ □ ABCD是菱形。
符号语言:
证明:
∵四边形ABCD是平行四边形,
∴OB=OD
又∵AC⊥BD
∴ □ ABCD是菱形
∴AB=AD
(有一组邻边相等的平行四边形是菱形)
(垂直平分线上的点到线段两端点的距离相等)
已知:在四边形ABCD中,
AB=BC=CD=DA
求证:四边形ABCD是菱形
∴四边形ABCD是平行四边形
证明:
∴四边形ABCD是菱形
(有一组邻边相等的平行四边形叫做菱形)
∵AD=BC AB=CD
又∵AB=AD
A
B
C
D
猜想:有四条边相等的四边形是菱形
探索,我能发现
已知:在四边形ABCD中,
AB=BC=CD=DA
求证:四边形ABCD是菱形
∴四边形ABCD是平行四边形
证明:
∴四边形ABCD是菱形
(有一组邻边相等的平行四边形叫做菱形)
∵AD=BC AB=CD
又∵AB=AD
A
B
C
D
有四条边相等的四边形是菱形
探索,我能发现
判定定理:
符号语言:
∵ AB=BC=CD=DA
∴四边形ABCD是菱形
一组邻边相等
对角线互相垂直
四条边相等
四边形
平行四边形
菱形
菱形的判定方法:
归纳,使我飞跃
1.________的平行四边形是菱形.
2.________的平行四边形是菱形.
3.________的四边形是菱形.
例3 如图,在□ ABCD中,对角线AC与BD
相交于点O,AB= ,AO=2,BO=1.
求证: □ ABCD是菱形
A
B
C
D
O
∴ □ ABCD是菱形.
证明:
∴
∴△OAB是直角三角形,∠ AOB是直角
∵AB= , AO=2,BO=1.
动手,我能提高
在△OAB中
∴ AC⊥BD
请用手中的尺规作一个边长为2厘米的菱形
动手,我能提高
练习,我能提升
1.将一张矩形纸对折再对折(如图),然后沿着图中的虚线剪下,得到①、②两部分,将①展开后得到的平面图形是( )
A.矩形 B.三角形 C.梯形 D.菱形
练习,我能提升
2.把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
E
F
收获和质疑
一组邻边相等
对角线互相垂直
四条边相等
四边形
平行四边形
菱形
菱形的判定方法:
猜想:
对角线互相垂直的平行四边形是菱形
猜想:
有四条边相等的四边形是菱形
已知:在□ABCD 中,对角线AC⊥BD
求证:□ABCD是菱形
O
猜想:对角线互相垂直的平行四边形是菱形
探索,我能发现
证明:
∵四边形ABCD是平行四边形,
∴OB=OD
又∵AC⊥BD
∴ □ ABCD是菱形
∴AB=AD
(有一组邻边相等的平行四边形是菱形)
(垂直平分线上的点到线段两端点的距离相等)
已知:在□ABCD 中,对角线AC⊥BD
求证:□ABCD是菱形
O
对角线互相垂直的平行四边形是菱形
探索,我能发现
判定定理:
∵四边形ABCD是平行四边形,
AC⊥BD,
∴ □ ABCD是菱形。
符号语言:
证明:
∵四边形ABCD是平行四边形,
∴OB=OD
又∵AC⊥BD
∴ □ ABCD是菱形
∴AB=AD
(有一组邻边相等的平行四边形是菱形)
(垂直平分线上的点到线段两端点的距离相等)
已知:在四边形ABCD中,
AB=BC=CD=DA
求证:四边形ABCD是菱形
∴四边形ABCD是平行四边形
证明:
∴四边形ABCD是菱形
(有一组邻边相等的平行四边形叫做菱形)
∵AD=BC AB=CD
又∵AB=AD
A
B
C
D
猜想:有四条边相等的四边形是菱形
探索,我能发现
已知:在四边形ABCD中,
AB=BC=CD=DA
求证:四边形ABCD是菱形
∴四边形ABCD是平行四边形
证明:
∴四边形ABCD是菱形
(有一组邻边相等的平行四边形叫做菱形)
∵AD=BC AB=CD
又∵AB=AD
A
B
C
D
有四条边相等的四边形是菱形
探索,我能发现
判定定理:
符号语言:
∵ AB=BC=CD=DA
∴四边形ABCD是菱形
一组邻边相等
对角线互相垂直
四条边相等
四边形
平行四边形
菱形
菱形的判定方法:
归纳,使我飞跃
1.________的平行四边形是菱形.
2.________的平行四边形是菱形.
3.________的四边形是菱形.
例3 如图,在□ ABCD中,对角线AC与BD
相交于点O,AB= ,AO=2,BO=1.
求证: □ ABCD是菱形
A
B
C
D
O
∴ □ ABCD是菱形.
证明:
∴
∴△OAB是直角三角形,∠ AOB是直角
∵AB= , AO=2,BO=1.
动手,我能提高
在△OAB中
∴ AC⊥BD
请用手中的尺规作一个边长为2厘米的菱形
动手,我能提高
练习,我能提升
1.将一张矩形纸对折再对折(如图),然后沿着图中的虚线剪下,得到①、②两部分,将①展开后得到的平面图形是( )
A.矩形 B.三角形 C.梯形 D.菱形
练习,我能提升
2.把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
E
F
