鲁教版(五四制)八年级下册数学 6.2.2矩形的判定 课件(25张)
文档属性
| 名称 | 鲁教版(五四制)八年级下册数学 6.2.2矩形的判定 课件(25张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-28 23:07:28 | ||
图片预览




文档简介
如图,在四边形ABCD中,对角
线AC,BD相交于点O,且AO=CO,BO=DO.
分别添加下列条件:
(1)∠ABC=90?
(2)AC⊥BD
(3)AC=BD
(4)AC平分∠BAD(5)AO=DO
使得四边形ABCD为矩形的条件的序号为
。
这节课你有什么收获?
有一个角是直角的平行四边形是矩形。
∵
四边形ABCD是平行四边形且∠A=90°
∴
□
ABCD是矩形
①
②
几何语言:
A
B
C
D
你还有其它的判定方法吗?
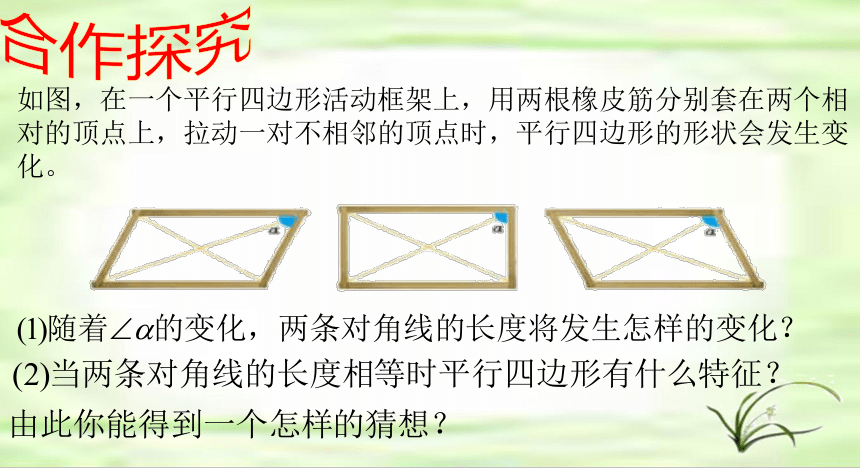
如图,在一个平行四边形活动框架上,用两根橡皮筋分别套在两个相对的顶点上,拉动一对不相邻的顶点时,平行四边形的形状会发生变化。
猜想:对角线相等的平行四边形是矩形.
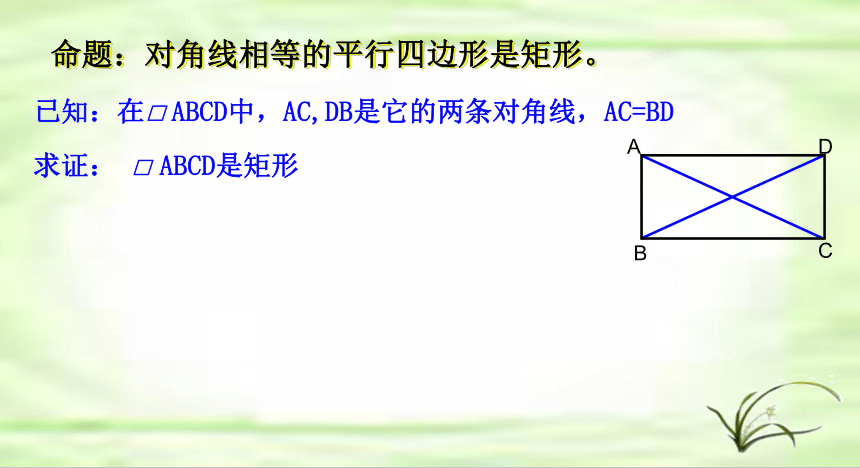
命题:对角线相等的平行四边形是矩形。
A
B
C
D
已知:在□
ABCD中,AC,DB是它的两条对角线,AC=BD
求证:
□
ABCD是矩形
命题:对角线相等的平行四边形是矩形。
A
B
C
D
证明:
∵
四边形ABCD是平行四边形,
∴AB=DC,AB∥DC.
又∵BC=CB,
AC=DB
∴
△ABC≌
△DCB(SSS)
∴
∠ABC=∠DCB
∵
AB//CD
∴
∠ABC+∠DCB=180°
∴
∠ABC=∠DCB=90°
又∵
四边形ABCD是平行四边形
∴
□
ABCD是矩形
(矩形的定义)
A
B
C
D
O
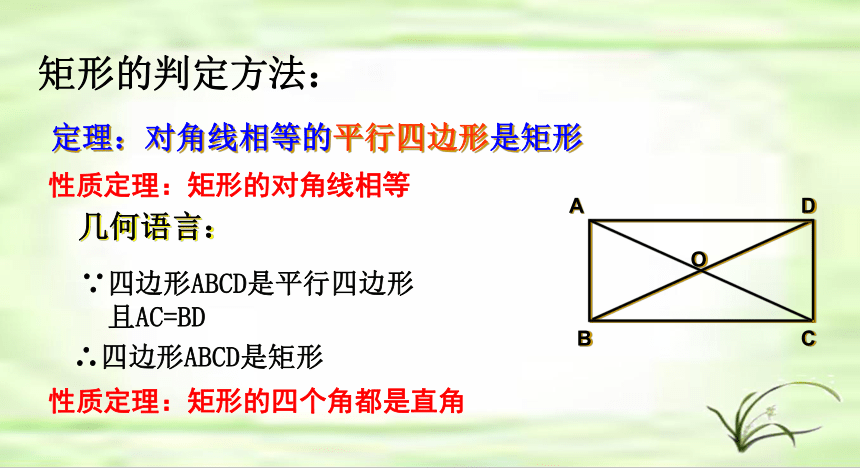
定理:对角线相等的平行四边形是矩形
几何语言:
∵四边形ABCD是平行四边形
且AC=BD
∴四边形ABCD是矩形
矩形的判定方法:
性质定理:矩形的对角线相等
性质定理:矩形的四个角都是直角
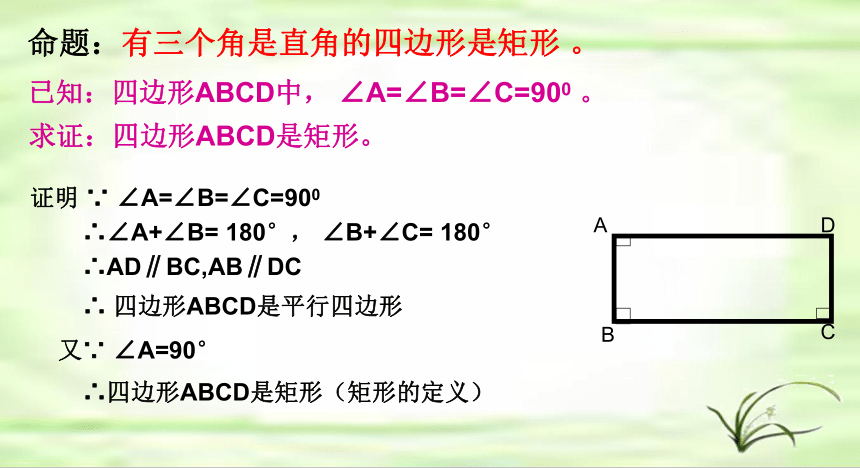
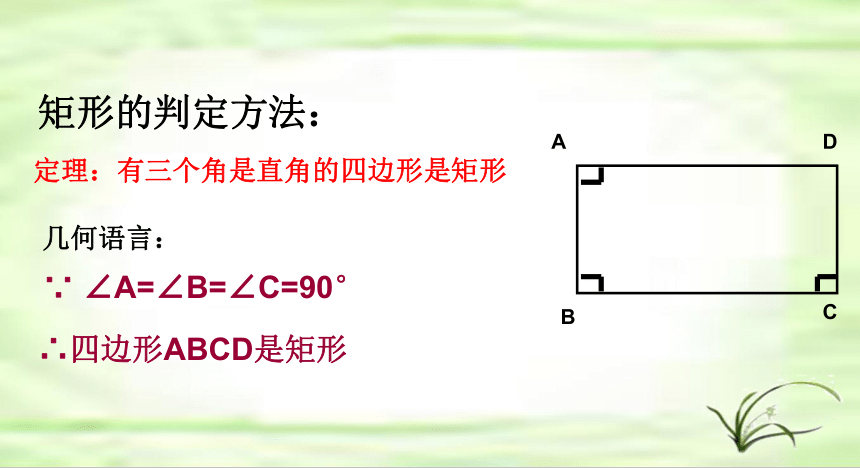
命题:有三个角是直角的四边形是矩形
。
已知:四边形ABCD中,
∠A=∠B=∠C=900
。
证明
∵
∠A=∠B=∠C=900
A
B
C
D
又∵
∠A=90°
∴AD∥BC,AB∥DC
∴
四边形ABCD是平行四边形
∴四边形ABCD是矩形(矩形的定义)
求证:四边形ABCD是矩形。
∴∠A+∠B=
180°,
∠B+∠C=
180°
矩形的判定方法:
定理:有三个角是直角的四边形是矩形
∵
∠A=∠B=∠C=90°学
科
网]
几何语言:
A
B
C
D
∴四边形ABCD是矩形[来源:
有一个角是直角的四边形是矩形吗?
有两个角是直角的四边形是矩形吗?
一个角是直角
对角线相等
三个角是直角
四边形
平行四边形
矩形
基础知识关
运用知识关
挑战中考关
(快速问答)
学以致用关
1、对角线相等的四边形是矩形。
一、判断
×
2、对角线互相平分且相等的四边形是矩形。
√
3、对角线相等且互相垂直的四边形是矩形。
×
4、对角线相等且有一个角是直角的四边形是矩形。
×
B
A
C
D
O
w
(1)(3)(5)
二、填空
例:如图,在□ABCD中,对角线AC
和BD
相交于点O,△ABO是等边三角形,AB=1.求□ABCD的面积.
A
B
C
D
O
例:如图,在□ABCD中,对角线AC
和BD
相交于点O,△ABO是等边三角形,AB=1.求□ABCD的面积.
A
B
C
D
O
解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
又∵△ABO是等边三角形,
∴OA=OB=AB=1,∠BAC=60°,
∴OA=OB=OC=OD=1.
∴AC=BD=2AB=2.
∴□
ABCD是矩形(对角线相等的平行四边形是矩形)
∴∠ABC=90°(矩形的四个角都是直角).
测量…?
现在你可以帮助木工朋友检测所制作的窗框是否
是矩形了吧,你可以测量哪些数据,有几种方案,
根据又是什么呢?
分别测量出两组对边的长度和一个内角的度数,如果两组对边的长度分别相等,且这个内角是直角,则窗框符合规格
方案:
测量出三个内角的度数,如果三个内角都是直角,则窗框符合规格
方案:
分别测量出窗框四边和两条对角线的长度,如果窗框两组对边长度、两条对角线的长度分别相等,那么窗框符合规格
方案:
分别测量出一组对边的长度和这组同旁内角的度数,如果这组对边的长度相等,且这两个内角都是直角,则窗框符合规格
方案:
挑战中考关
(2008
南京中考)已知:在平行四边形ABCD中,AF.BE.CH.DG分别是它的四个内角的平分线.求证:四边形EFGH是矩形.
A
B
D
C
H
E
F
G
∵四边形ABCD是平行四边形
∴AB∥CD
∴∠DAB+∠ABC=180
°
证明:
同理:∠EFG=90°、∠FGH=90°
∴四边形EFGH是矩形
∵AF、BE分别平分∠DAB、∠ABC
∴∠EAB+∠EBA=90
°
∴∠AEB=90°
即∠HEF=90°
B
A
C
D
O
P
N
M
F
E
已知:AD∥BC,ME、NE、MF、NF分别为角平分线。
求证:四边形ABCD为矩形
∵AD∥BC
∴∠AMN+∠BNM=180
°
∵ME、NE分别平分∠AMN、∠BNM
∴∠EMN+∠ENM=90
°
∴∠MEN=90
°
同理:∠MFN=90
°
∵∠BMN+∠CNM=180
°
NE、NF分别平分∠BMN、∠CNM
∴∠EMN+∠FNM=90
°
∴∠ENF=90°
∴四边形ABCD为矩形
课堂小结
∠A=
∠B=
∠C=90°
AC
=
BD或∠ABC=90?
ABCD
ABCD
是矩形
四边形ABCD
是矩形
线AC,BD相交于点O,且AO=CO,BO=DO.
分别添加下列条件:
(1)∠ABC=90?
(2)AC⊥BD
(3)AC=BD
(4)AC平分∠BAD(5)AO=DO
使得四边形ABCD为矩形的条件的序号为
。
这节课你有什么收获?
有一个角是直角的平行四边形是矩形。
∵
四边形ABCD是平行四边形且∠A=90°
∴
□
ABCD是矩形
①
②
几何语言:
A
B
C
D
你还有其它的判定方法吗?
如图,在一个平行四边形活动框架上,用两根橡皮筋分别套在两个相对的顶点上,拉动一对不相邻的顶点时,平行四边形的形状会发生变化。
猜想:对角线相等的平行四边形是矩形.
命题:对角线相等的平行四边形是矩形。
A
B
C
D
已知:在□
ABCD中,AC,DB是它的两条对角线,AC=BD
求证:
□
ABCD是矩形
命题:对角线相等的平行四边形是矩形。
A
B
C
D
证明:
∵
四边形ABCD是平行四边形,
∴AB=DC,AB∥DC.
又∵BC=CB,
AC=DB
∴
△ABC≌
△DCB(SSS)
∴
∠ABC=∠DCB
∵
AB//CD
∴
∠ABC+∠DCB=180°
∴
∠ABC=∠DCB=90°
又∵
四边形ABCD是平行四边形
∴
□
ABCD是矩形
(矩形的定义)
A
B
C
D
O
定理:对角线相等的平行四边形是矩形
几何语言:
∵四边形ABCD是平行四边形
且AC=BD
∴四边形ABCD是矩形
矩形的判定方法:
性质定理:矩形的对角线相等
性质定理:矩形的四个角都是直角
命题:有三个角是直角的四边形是矩形
。
已知:四边形ABCD中,
∠A=∠B=∠C=900
。
证明
∵
∠A=∠B=∠C=900
A
B
C
D
又∵
∠A=90°
∴AD∥BC,AB∥DC
∴
四边形ABCD是平行四边形
∴四边形ABCD是矩形(矩形的定义)
求证:四边形ABCD是矩形。
∴∠A+∠B=
180°,
∠B+∠C=
180°
矩形的判定方法:
定理:有三个角是直角的四边形是矩形
∵
∠A=∠B=∠C=90°学
科
网]
几何语言:
A
B
C
D
∴四边形ABCD是矩形[来源:
有一个角是直角的四边形是矩形吗?
有两个角是直角的四边形是矩形吗?
一个角是直角
对角线相等
三个角是直角
四边形
平行四边形
矩形
基础知识关
运用知识关
挑战中考关
(快速问答)
学以致用关
1、对角线相等的四边形是矩形。
一、判断
×
2、对角线互相平分且相等的四边形是矩形。
√
3、对角线相等且互相垂直的四边形是矩形。
×
4、对角线相等且有一个角是直角的四边形是矩形。
×
B
A
C
D
O
w
(1)(3)(5)
二、填空
例:如图,在□ABCD中,对角线AC
和BD
相交于点O,△ABO是等边三角形,AB=1.求□ABCD的面积.
A
B
C
D
O
例:如图,在□ABCD中,对角线AC
和BD
相交于点O,△ABO是等边三角形,AB=1.求□ABCD的面积.
A
B
C
D
O
解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
又∵△ABO是等边三角形,
∴OA=OB=AB=1,∠BAC=60°,
∴OA=OB=OC=OD=1.
∴AC=BD=2AB=2.
∴□
ABCD是矩形(对角线相等的平行四边形是矩形)
∴∠ABC=90°(矩形的四个角都是直角).
测量…?
现在你可以帮助木工朋友检测所制作的窗框是否
是矩形了吧,你可以测量哪些数据,有几种方案,
根据又是什么呢?
分别测量出两组对边的长度和一个内角的度数,如果两组对边的长度分别相等,且这个内角是直角,则窗框符合规格
方案:
测量出三个内角的度数,如果三个内角都是直角,则窗框符合规格
方案:
分别测量出窗框四边和两条对角线的长度,如果窗框两组对边长度、两条对角线的长度分别相等,那么窗框符合规格
方案:
分别测量出一组对边的长度和这组同旁内角的度数,如果这组对边的长度相等,且这两个内角都是直角,则窗框符合规格
方案:
挑战中考关
(2008
南京中考)已知:在平行四边形ABCD中,AF.BE.CH.DG分别是它的四个内角的平分线.求证:四边形EFGH是矩形.
A
B
D
C
H
E
F
G
∵四边形ABCD是平行四边形
∴AB∥CD
∴∠DAB+∠ABC=180
°
证明:
同理:∠EFG=90°、∠FGH=90°
∴四边形EFGH是矩形
∵AF、BE分别平分∠DAB、∠ABC
∴∠EAB+∠EBA=90
°
∴∠AEB=90°
即∠HEF=90°
B
A
C
D
O
P
N
M
F
E
已知:AD∥BC,ME、NE、MF、NF分别为角平分线。
求证:四边形ABCD为矩形
∵AD∥BC
∴∠AMN+∠BNM=180
°
∵ME、NE分别平分∠AMN、∠BNM
∴∠EMN+∠ENM=90
°
∴∠MEN=90
°
同理:∠MFN=90
°
∵∠BMN+∠CNM=180
°
NE、NF分别平分∠BMN、∠CNM
∴∠EMN+∠FNM=90
°
∴∠ENF=90°
∴四边形ABCD为矩形
课堂小结
∠A=
∠B=
∠C=90°
AC
=
BD或∠ABC=90?
ABCD
ABCD
是矩形
四边形ABCD
是矩形
