6.2.2 排列数-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册课件(18张PPT)
文档属性
| 名称 | 6.2.2 排列数-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册课件(18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 254.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-28 21:24:52 | ||
图片预览






文档简介
6.2.2 排列数
复习引入
一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列(arrangement).
1.排列的定义:
2、排列问题的判断方法:
(1) 元素的无重复性
(2) 元素的有序性
判断关键是看选出的元素有没有顺序要求。
1. 能在排列的基础上给出排列数的定义和表示,并能区别排列与排列数。
2. 通过利用计数原理分析和解决具体的排列问题,得到排列数公式,并能利用公式求具体问题的排列数。
重点:排列数公式;
难点:排列数公式的应用。
问题1:在6.2.1节问题1、问题2中,我们是根据计数原理和列举数数的方式得到排列的个数.但随着元素个数的增加,这样的方法就越来越烦琐了。是否有计算排列个数的公式,从而能便捷地求出排列的个数?
排列数的定义和表示:把从n个不同元素中取出m(m≤n)个元素的所有不同排列的个数,叫做从n个不同元素中取出m个元素的排列数,并用符号 表示。
追问1:6.2.1节问题1、问题2的排列数,并说明排列数与排列有何区别.
6.2.1问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
6.2.1问题2:从1,2,3,4这4个数字中,每次取出3个排成一个三位数,共可得到多少个不同的三位数?
一个排列就是完成一件事的一种方法,它不是数;排列数是所有排列的个数,它是一个数。
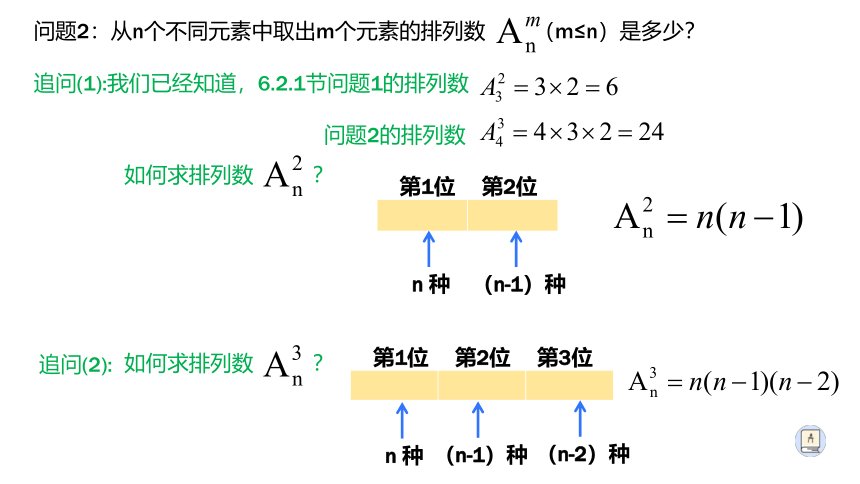
问题2:从n个不同元素中取出m个元素的排列数 (m≤n)是多少?
追问(1):我们已经知道,6.2.1节问题1的排列数
问题2的排列数
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
第1位
第2位
n 种
(n-1)种
如何求排列数 ?
追问(2):
如何求排列数 ?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
第1位
第2位
n 种
(n-1)种
第3位
(n-2)种
概念新授
一般地:假定有排好顺序的m个空位,从n个不同元素中取出m个元素去填空,一个空位填上一个元素,每一种填法就对应一个排列.因此,所有不同填法的种数就是排列数 .利用分步乘法计数原理计算填法的种数,得到排列数公式:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
第1位
第2位
n 种
(n-1)种
第3位
(n-(m-1))种
第m位
(n-2)种
问题3:上述排列数公式有什么特点?使用公式需要注意什么?
(1)观察公式的右边,共有几个因数?各因数的大小有什么规律?
(2)比较n与m的大小关系,并说明公式右边的最后一个因数有什么特点?
(3)利用排列数公式,计算 。
......
排列数公式
的连乘形式
特别地,我们把n个不同的元素全部取出的一个排列,叫做n个元素的一个全排列.
将n个不同的元素全部取出的排列数,等于正整数1到n的连乘积.正整数1到n的连乘积,叫做n的阶乘,用n!表示.于是,n个元素的全排列数公式可以写成
我们规定,0!=1
追问1:你能写一下常见自然数的阶乘吗?
1!=1;
2!=2?1=2
3!=3?2?1=6
4!=4?3?2?1=24
例3:计算:
问题4:由例3可以看到,
观察这两个结果,从中你发现它们的共性吗?
解:根据排列数公式,可得:
问题4:由例3可以看到,
观察这两个结果,从中你发现它们的共性吗?
排列数公式
的阶乘形式
排列数公式
的连乘形式
问题5:证明:(1) ; (2) ;
排列数的性质:
性质1:
性质2:
证明:
(1)
(2)
练习1:证明:
排列数的性质:
性质1:
性质2:
证明:
例4:用0~9这10个数字,可以组成多少个没有重复数字的三位数?
分析:在0~9这10个数字中,因为0不能在百位上,而其他9个数字可以在任意数位上,因此0是一个特殊的元素.一般地,我们可以从特殊元素的位置入手来考虑问题。
解法1:由于三位数的百位上的数字不能是0,所以可以分两步完成:
第1步,确定百位上的数字,可以从1~9这9个数字中取出1个,有 种取法;
第2步,确定十位和个位上的数字,可以从剩下的9个数字中取出2个,有 种取法.
根据分步乘法计数原理,所求的三位数的个数为:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
百位
十位
个位
例4:用0~9这10个数字,可以组成多少个没有重复数字的三位数?
解法2:符合条件的三位数可以分成三类:
第1类,每一位数字都不是0的三位数,可以从1~9这9个数字中取出3个,有 种取法;
第2类,个位上的数字是0的三位数,可以从剩下的9个数字中取出2个放在百位和十位,有 种取法;
第3类,十位上的数字是0的三位数,可以从剩下的9个数字中取出2个放在百位和个位,有 种取法.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
百位
十位
个位
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
0
百位
十位
个位
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
0
百位
十位
个位
例4:用0~9这10个数字,可以组成多少个没有重复数字的三位数?
解法3: 从0~9这10个数字中选取3个的排列数为 ,其中0在百位上的排列数为 ,它们的差就是用这10个数组成的没有重复数字的三位数的个数,即所求三位数的个数为
方法归纳:
1.求解排列问题的方法:
(1)判断排列问题;
(2)根据计数原理给出用排列数符号表示的运算式子;
(3)利用排列数公式求出结果。
2.带有限制条件的排列问题:“特殊”优先原则
直接法
间接法
位置分析法
元素分析法
以位置为主,优先考虑特殊位置
以元素为主,优先考虑特殊元素
先不考虑限制条件而计算出来所有排列数,再从中减去全部不符合条件的排列数,从而得出符合条件的排列数
课堂小结
2.排列数公式:
1. 排列数的定义和表示:
3.n个元素的全排列数公式:
0!=1
把从n个不同元素中取出m(m≤n)个元素的所有不同排列的个数,叫做从n个不同元素中取出m个元素的排列数,并用符号 表示。
4.求解排列问题的方法:
(1)判断排列问题;
(2)根据计数原理给出用排列数符号表示的运算式子;
(3)利用排列数公式求出结果。
整理笔记:
课本P20,练习1、2、3
习题6.2 1、4(2),(3),(4)、8、11、19;
复习引入
一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列(arrangement).
1.排列的定义:
2、排列问题的判断方法:
(1) 元素的无重复性
(2) 元素的有序性
判断关键是看选出的元素有没有顺序要求。
1. 能在排列的基础上给出排列数的定义和表示,并能区别排列与排列数。
2. 通过利用计数原理分析和解决具体的排列问题,得到排列数公式,并能利用公式求具体问题的排列数。
重点:排列数公式;
难点:排列数公式的应用。
问题1:在6.2.1节问题1、问题2中,我们是根据计数原理和列举数数的方式得到排列的个数.但随着元素个数的增加,这样的方法就越来越烦琐了。是否有计算排列个数的公式,从而能便捷地求出排列的个数?
排列数的定义和表示:把从n个不同元素中取出m(m≤n)个元素的所有不同排列的个数,叫做从n个不同元素中取出m个元素的排列数,并用符号 表示。
追问1:6.2.1节问题1、问题2的排列数,并说明排列数与排列有何区别.
6.2.1问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
6.2.1问题2:从1,2,3,4这4个数字中,每次取出3个排成一个三位数,共可得到多少个不同的三位数?
一个排列就是完成一件事的一种方法,它不是数;排列数是所有排列的个数,它是一个数。
问题2:从n个不同元素中取出m个元素的排列数 (m≤n)是多少?
追问(1):我们已经知道,6.2.1节问题1的排列数
问题2的排列数
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
第1位
第2位
n 种
(n-1)种
如何求排列数 ?
追问(2):
如何求排列数 ?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
第1位
第2位
n 种
(n-1)种
第3位
(n-2)种
概念新授
一般地:假定有排好顺序的m个空位,从n个不同元素中取出m个元素去填空,一个空位填上一个元素,每一种填法就对应一个排列.因此,所有不同填法的种数就是排列数 .利用分步乘法计数原理计算填法的种数,得到排列数公式:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
第1位
第2位
n 种
(n-1)种
第3位
(n-(m-1))种
第m位
(n-2)种
问题3:上述排列数公式有什么特点?使用公式需要注意什么?
(1)观察公式的右边,共有几个因数?各因数的大小有什么规律?
(2)比较n与m的大小关系,并说明公式右边的最后一个因数有什么特点?
(3)利用排列数公式,计算 。
......
排列数公式
的连乘形式
特别地,我们把n个不同的元素全部取出的一个排列,叫做n个元素的一个全排列.
将n个不同的元素全部取出的排列数,等于正整数1到n的连乘积.正整数1到n的连乘积,叫做n的阶乘,用n!表示.于是,n个元素的全排列数公式可以写成
我们规定,0!=1
追问1:你能写一下常见自然数的阶乘吗?
1!=1;
2!=2?1=2
3!=3?2?1=6
4!=4?3?2?1=24
例3:计算:
问题4:由例3可以看到,
观察这两个结果,从中你发现它们的共性吗?
解:根据排列数公式,可得:
问题4:由例3可以看到,
观察这两个结果,从中你发现它们的共性吗?
排列数公式
的阶乘形式
排列数公式
的连乘形式
问题5:证明:(1) ; (2) ;
排列数的性质:
性质1:
性质2:
证明:
(1)
(2)
练习1:证明:
排列数的性质:
性质1:
性质2:
证明:
例4:用0~9这10个数字,可以组成多少个没有重复数字的三位数?
分析:在0~9这10个数字中,因为0不能在百位上,而其他9个数字可以在任意数位上,因此0是一个特殊的元素.一般地,我们可以从特殊元素的位置入手来考虑问题。
解法1:由于三位数的百位上的数字不能是0,所以可以分两步完成:
第1步,确定百位上的数字,可以从1~9这9个数字中取出1个,有 种取法;
第2步,确定十位和个位上的数字,可以从剩下的9个数字中取出2个,有 种取法.
根据分步乘法计数原理,所求的三位数的个数为:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
百位
十位
个位
例4:用0~9这10个数字,可以组成多少个没有重复数字的三位数?
解法2:符合条件的三位数可以分成三类:
第1类,每一位数字都不是0的三位数,可以从1~9这9个数字中取出3个,有 种取法;
第2类,个位上的数字是0的三位数,可以从剩下的9个数字中取出2个放在百位和十位,有 种取法;
第3类,十位上的数字是0的三位数,可以从剩下的9个数字中取出2个放在百位和个位,有 种取法.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
百位
十位
个位
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
0
百位
十位
个位
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
0
百位
十位
个位
例4:用0~9这10个数字,可以组成多少个没有重复数字的三位数?
解法3: 从0~9这10个数字中选取3个的排列数为 ,其中0在百位上的排列数为 ,它们的差就是用这10个数组成的没有重复数字的三位数的个数,即所求三位数的个数为
方法归纳:
1.求解排列问题的方法:
(1)判断排列问题;
(2)根据计数原理给出用排列数符号表示的运算式子;
(3)利用排列数公式求出结果。
2.带有限制条件的排列问题:“特殊”优先原则
直接法
间接法
位置分析法
元素分析法
以位置为主,优先考虑特殊位置
以元素为主,优先考虑特殊元素
先不考虑限制条件而计算出来所有排列数,再从中减去全部不符合条件的排列数,从而得出符合条件的排列数
课堂小结
2.排列数公式:
1. 排列数的定义和表示:
3.n个元素的全排列数公式:
0!=1
把从n个不同元素中取出m(m≤n)个元素的所有不同排列的个数,叫做从n个不同元素中取出m个元素的排列数,并用符号 表示。
4.求解排列问题的方法:
(1)判断排列问题;
(2)根据计数原理给出用排列数符号表示的运算式子;
(3)利用排列数公式求出结果。
整理笔记:
课本P20,练习1、2、3
习题6.2 1、4(2),(3),(4)、8、11、19;
