6.2.3 组合-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册课件(13张PPT)
文档属性
| 名称 | 6.2.3 组合-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册课件(13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 223.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-28 21:25:45 | ||
图片预览





文档简介
6.2.3 组合
重点:组合的定义。
难点:将实际问题中的具体对象抽象为元素,得到组合的定义。
1.过解决实际的计数问题,得到组合的定义;
2.能利用定义判断组合问题,知道组合问题与排列问题的区别与联系。
追问1:问题1中要完成的“一件事情”是什么?比较6.2.1节问题1与本节问题1中要完成的“一件事情”,它们有什么异同?
6.2.1问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,有多少种不同的选法?这一问题与6.2.1节的问题1有什么联系与区别?
追问2:列出问题1的各种不同选法,与6.2.1节问题1的选法相比,它们有什么不同?是否与顺序有关?
本节问题1:“选出2名参加一项活动”
6.2.1节问题1:“选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动”
本节问题1:
6.2.1节问题1:
甲乙,甲丙,乙丙
甲乙,乙甲,甲丙,丙甲,乙丙,丙乙
与顺序无关
与顺序有关
问题2:如果将问题1的背景去掉,把被选出的同学叫做元素,那么还可怎样表述问题1?你能将它推广到一般情形吗?
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,有多少种不同的选法?
将具体背景舍去,问题1可以概括为:
从3个不同元素中取出2个元素作为一组,一共有多少个不同的组?
一般地,从n个不同元素中取出m(m≤n)个元素作为一组,叫做从n个不同元素中取出m个元素的一个组合(combination).
注意:
(1)组合的特点:组合要求n个元素是不同的,取出的m个元素也是不同的,即从n个不同的元素中进行m次不放回地取出.
(2)组合的特性:元素的无序性。取出的m个元素不讲究顺序,即元素没有位置的要求。
小试牛刀
(1)设集合A={a,b,c,d,e),则集合A的子集中含有3个元素的有多少个?
(2)某铁路线上有5个车站,则这条线上有多少种票价?
(3)3人去干5种不同的工作,每人干1种,有多少种分工方法?
(4)把3本相同的书分给5个学生,每人最多得1本,有几种分配方法?
A.(1)(2)(4)B.(1)(3)(4)C.(2)(3)(4)D.(1)(2)(3)
1.下列问题是组合问题的有( )
解析:根据组合定义知(1)(2)(4)是组合问题.
答案:A
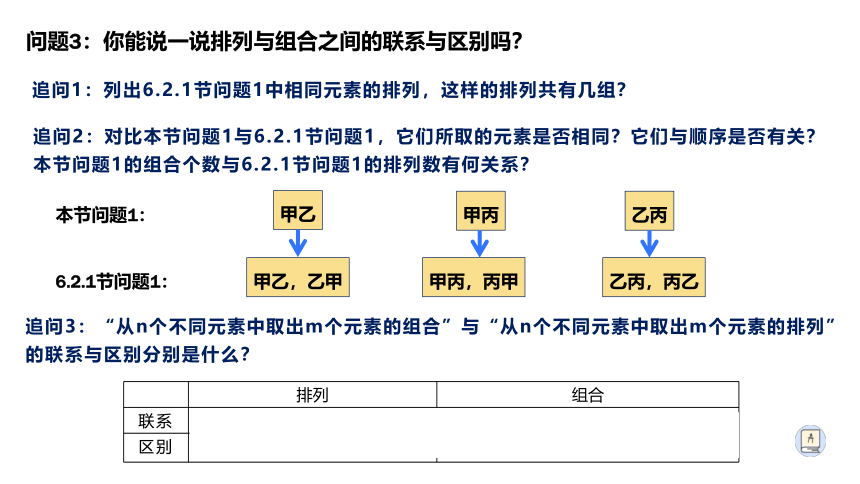
问题3:你能说一说排列与组合之间的联系与区别吗?
追问3:“从n个不同元素中取出m个元素的组合”与“从n个不同元素中取出m个元素的排列”的联系与区别分别是什么?
追问1:列出6.2.1节问题1中相同元素的排列,这样的排列共有几组?
追问2:对比本节问题1与6.2.1节问题1,它们所取的元素是否相同?它们与顺序是否有关?本节问题1的组合个数与6.2.1节问题1的排列数有何关系?
本节问题1:
6.2.1节问题1:
甲乙,乙甲
甲丙,丙甲
乙丙,丙乙
甲乙
甲丙
乙丙
{5940675A-B579-460E-94D1-54222C63F5DA}
排列
组合
联系
从n个不同元素中取出m个元素
区别
与元素的顺序有关
与元素的顺序无关
追问4:校门口停放着9辆共享自行车,其中黄色、红色和绿色的各有3辆。下面的问题:(1)从中选3辆,有多少种不同的方法?
(2)从中选3辆给3位同学,有多少种不同的方法?
在(1)中,选出3辆车即可,没有顺序,是一个组合问题;
在(2)中,不仅要选出3辆车,还要分配给3位同学,有顺序,是一个排列问题 .
追问5:如何区分排列问题还是组合问题?
{5940675A-B579-460E-94D1-54222C63F5DA}排列问题
组合问题
若交换某两个元素的位置对结果有影响,则是排列问题,即排列问题与选取的顺序有关.
若交换任意两个元素的位置对结果没有影响,则是组合问题,即组合问题与选取的顺序无关.
典例分析
例1:平面内有A,B,C,D 4个点.
(1)以其中2个点为端点的有向线段共有多少条?
(2)以其中2个点为端点的线段共有多少条?
分析:(1)要完成的“一件事情”是什么? (2)完成的“一件事情”是否与“顺序”有关?
解:(1)一条有向线段的两个端点要分起点和终点,以平面内4个点中的2个为端点的有向线段的条数,就是从4个不同元素中取出2个元素的排列数,即有向线段条数为????????????=????×????=????????.
这12条有向线段分别为:????????, ?????????, ????????, ?????????, ????????, ????????, ????????, ?????????,?????????, ????????, ????????, ????????
(2)由于不考虑两个端点的顺序,因此将(1)中端点相同、方向不同的2条有向线段作为一条线段,就是以平面内4个点中的2个点为端点的线段的条数,共有如下6条:AB,AC,AD,BC,BD,CD.
?
方法梳理
(1)判断是否为组合问题;
(2)是否分类或分步;
(3)根据组合的相关知识进行求解.
1.求一个组合问题的所有组合个数的基本方法:
2.思考:利用排列和组合之间的关系,以“元素相同”为标准分类,你能建立起例5(1)中排列和(2)中组合之间的对应关系吗?进一步地,能否从这种对应关系出发,由排列数求出组合的个数?
取出2个元素的组合的个数
是排列数的一半
课堂小结
(2)如何判断一个计数问题是排列问题还是组合问题?
{5940675A-B579-460E-94D1-54222C63F5DA}排列问题
组合问题
若交换某两个元素的位置对结果有影响,则是排列问题,即排列问题与选取的顺序有关.
若交换任意两个元素的位置对结果没有影响,则是组合问题,即组合问题与选取的顺序无关.
一般地,从n个不同元素中取出m(m≤n)个元素作为一组,叫做从n个不同元素中取出m个元素的一个组合(combination).
(1)组合的定义?
课堂小结
(3)求一个组合问题的所有组合个数的基本方法:
(1)判断是否为组合问题;
(2)是否分类或分步;
(3)根据组合的相关知识进行求解.
课本习题6.2第4,7题。
重点:组合的定义。
难点:将实际问题中的具体对象抽象为元素,得到组合的定义。
1.过解决实际的计数问题,得到组合的定义;
2.能利用定义判断组合问题,知道组合问题与排列问题的区别与联系。
追问1:问题1中要完成的“一件事情”是什么?比较6.2.1节问题1与本节问题1中要完成的“一件事情”,它们有什么异同?
6.2.1问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,有多少种不同的选法?这一问题与6.2.1节的问题1有什么联系与区别?
追问2:列出问题1的各种不同选法,与6.2.1节问题1的选法相比,它们有什么不同?是否与顺序有关?
本节问题1:“选出2名参加一项活动”
6.2.1节问题1:“选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动”
本节问题1:
6.2.1节问题1:
甲乙,甲丙,乙丙
甲乙,乙甲,甲丙,丙甲,乙丙,丙乙
与顺序无关
与顺序有关
问题2:如果将问题1的背景去掉,把被选出的同学叫做元素,那么还可怎样表述问题1?你能将它推广到一般情形吗?
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,有多少种不同的选法?
将具体背景舍去,问题1可以概括为:
从3个不同元素中取出2个元素作为一组,一共有多少个不同的组?
一般地,从n个不同元素中取出m(m≤n)个元素作为一组,叫做从n个不同元素中取出m个元素的一个组合(combination).
注意:
(1)组合的特点:组合要求n个元素是不同的,取出的m个元素也是不同的,即从n个不同的元素中进行m次不放回地取出.
(2)组合的特性:元素的无序性。取出的m个元素不讲究顺序,即元素没有位置的要求。
小试牛刀
(1)设集合A={a,b,c,d,e),则集合A的子集中含有3个元素的有多少个?
(2)某铁路线上有5个车站,则这条线上有多少种票价?
(3)3人去干5种不同的工作,每人干1种,有多少种分工方法?
(4)把3本相同的书分给5个学生,每人最多得1本,有几种分配方法?
A.(1)(2)(4)B.(1)(3)(4)C.(2)(3)(4)D.(1)(2)(3)
1.下列问题是组合问题的有( )
解析:根据组合定义知(1)(2)(4)是组合问题.
答案:A
问题3:你能说一说排列与组合之间的联系与区别吗?
追问3:“从n个不同元素中取出m个元素的组合”与“从n个不同元素中取出m个元素的排列”的联系与区别分别是什么?
追问1:列出6.2.1节问题1中相同元素的排列,这样的排列共有几组?
追问2:对比本节问题1与6.2.1节问题1,它们所取的元素是否相同?它们与顺序是否有关?本节问题1的组合个数与6.2.1节问题1的排列数有何关系?
本节问题1:
6.2.1节问题1:
甲乙,乙甲
甲丙,丙甲
乙丙,丙乙
甲乙
甲丙
乙丙
{5940675A-B579-460E-94D1-54222C63F5DA}
排列
组合
联系
从n个不同元素中取出m个元素
区别
与元素的顺序有关
与元素的顺序无关
追问4:校门口停放着9辆共享自行车,其中黄色、红色和绿色的各有3辆。下面的问题:(1)从中选3辆,有多少种不同的方法?
(2)从中选3辆给3位同学,有多少种不同的方法?
在(1)中,选出3辆车即可,没有顺序,是一个组合问题;
在(2)中,不仅要选出3辆车,还要分配给3位同学,有顺序,是一个排列问题 .
追问5:如何区分排列问题还是组合问题?
{5940675A-B579-460E-94D1-54222C63F5DA}排列问题
组合问题
若交换某两个元素的位置对结果有影响,则是排列问题,即排列问题与选取的顺序有关.
若交换任意两个元素的位置对结果没有影响,则是组合问题,即组合问题与选取的顺序无关.
典例分析
例1:平面内有A,B,C,D 4个点.
(1)以其中2个点为端点的有向线段共有多少条?
(2)以其中2个点为端点的线段共有多少条?
分析:(1)要完成的“一件事情”是什么? (2)完成的“一件事情”是否与“顺序”有关?
解:(1)一条有向线段的两个端点要分起点和终点,以平面内4个点中的2个为端点的有向线段的条数,就是从4个不同元素中取出2个元素的排列数,即有向线段条数为????????????=????×????=????????.
这12条有向线段分别为:????????, ?????????, ????????, ?????????, ????????, ????????, ????????, ?????????,?????????, ????????, ????????, ????????
(2)由于不考虑两个端点的顺序,因此将(1)中端点相同、方向不同的2条有向线段作为一条线段,就是以平面内4个点中的2个点为端点的线段的条数,共有如下6条:AB,AC,AD,BC,BD,CD.
?
方法梳理
(1)判断是否为组合问题;
(2)是否分类或分步;
(3)根据组合的相关知识进行求解.
1.求一个组合问题的所有组合个数的基本方法:
2.思考:利用排列和组合之间的关系,以“元素相同”为标准分类,你能建立起例5(1)中排列和(2)中组合之间的对应关系吗?进一步地,能否从这种对应关系出发,由排列数求出组合的个数?
取出2个元素的组合的个数
是排列数的一半
课堂小结
(2)如何判断一个计数问题是排列问题还是组合问题?
{5940675A-B579-460E-94D1-54222C63F5DA}排列问题
组合问题
若交换某两个元素的位置对结果有影响,则是排列问题,即排列问题与选取的顺序有关.
若交换任意两个元素的位置对结果没有影响,则是组合问题,即组合问题与选取的顺序无关.
一般地,从n个不同元素中取出m(m≤n)个元素作为一组,叫做从n个不同元素中取出m个元素的一个组合(combination).
(1)组合的定义?
课堂小结
(3)求一个组合问题的所有组合个数的基本方法:
(1)判断是否为组合问题;
(2)是否分类或分步;
(3)根据组合的相关知识进行求解.
课本习题6.2第4,7题。
