6.3.1 二项式定理-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册课件(22张PPT)
文档属性
| 名称 | 6.3.1 二项式定理-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册课件(22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 654.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-28 00:00:00 | ||
图片预览







文档简介
6.3.1 二项式定理
艾萨克·牛顿 Isaac Newton (1643—1727) 英国科学家.他被誉为人类历史上最伟大的科学家之一.他不仅是一位物理学家、天文学家,还是一位伟大的数学家.
牛顿二项式定理
(1)利用计数原理分析二项式的展开过程,归纳、猜想出二项式定理,并用计数原理加以证明;
(2)会应用二项式定理求解二项展开式;
(3)通过经历二项式定理的探究过程,体验“归纳、猜想、证明”的数学发现过程,提高自己观察、分析、概括的能力,以及 “从特殊到一般”、“从一般到特殊”等数学思想的应用能力;
(4)感受二项式定理体现出的数学的内在和谐、对称美,了解相关数学史内容.
项的形式:
a2
ab
ba
b2
思考: 同类项的个数?
2个(a+b)都不选b得到的,因此a2出现的次数相当于从2个(a+b)中取0个b(即都取a)的组合数 ,即a2只有1个;
由1个(a+b)中选a,另1个(a+b)中选b得到的.由于b选定后,a的选法也随之确定,因此,ab出现的次数相当于从2个(a+b)中取1个b的组合数 ,即ab共有2个.
由2个(a+b)中都选b得到的.因此,b2出现的次数相当于从2个(a+b)中取2个b的组合数 ,即b2只有1个.
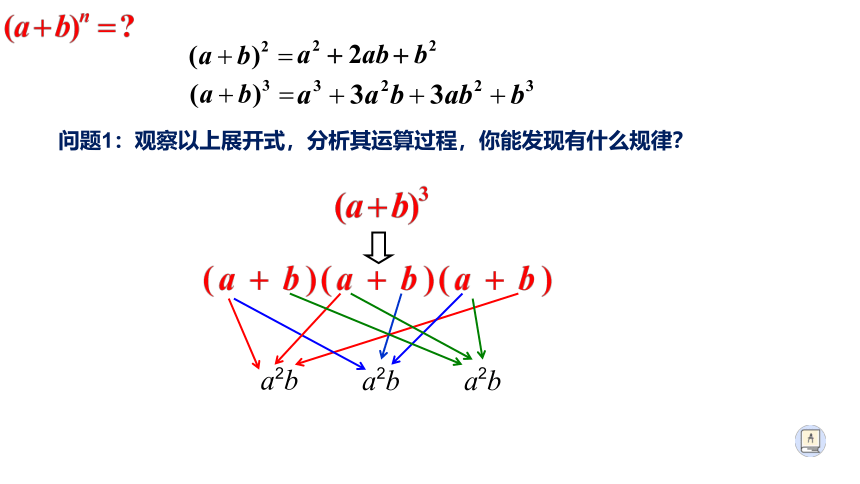
问题1:观察以上展开式,分析其运算过程,你能发现有什么规律?
a3
问题1:观察以上展开式,分析其运算过程,你能发现有什么规律?
a2b
a2b
a2b
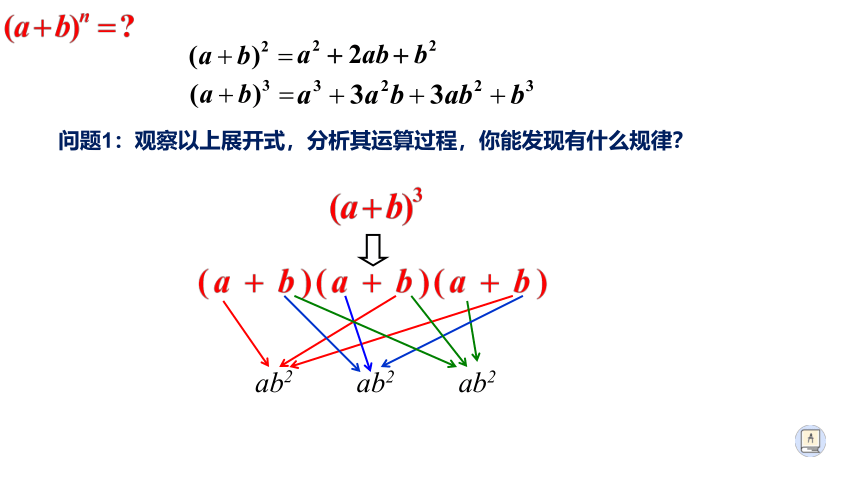
问题1:观察以上展开式,分析其运算过程,你能发现有什么规律?
ab2
ab2
ab2
问题1:观察以上展开式,分析其运算过程,你能发现有什么规律?
b3
展开式共有:
项的形式:
思考: 同类项的个数?
a4
a3b
ab3
b4
a2b2
问题2:你能写出(a+b)4的展开式吗?
证明:
(项的结构)
问题3:写出(a+b)n的展开式?
证明:
(项的系数)
问题3:写出(a+b)n的展开式?
(1)展开式共有 项.
(2)各项的次数都等于二项式的次数n;
字母a按降幂排列,次数由n递减到0;
字母b按升幂排列,次数由0递增到n.
(4)二项展开式中,系数 叫作二项式系数,即
n+1
注意:
二项式定理
思考:
例1、
求 的展开式.
解:根据二项式定理,
变式1:
求 的展开式.
解:根据二项式定理,
例2:
例2:
解:
(1)
(2)
(3)
解:
求 的展开式中 的系数。
的展开式的通项:
根据题意,得
因此, 的系数是
例3:
课堂小结
1、二项式定理
2、二项展开式的通项
3、二项式系数:
艾萨克·牛顿 Isaac Newton (1643—1727) 英国科学家.他被誉为人类历史上最伟大的科学家之一.他不仅是一位物理学家、天文学家,还是一位伟大的数学家.
牛顿二项式定理
(1)利用计数原理分析二项式的展开过程,归纳、猜想出二项式定理,并用计数原理加以证明;
(2)会应用二项式定理求解二项展开式;
(3)通过经历二项式定理的探究过程,体验“归纳、猜想、证明”的数学发现过程,提高自己观察、分析、概括的能力,以及 “从特殊到一般”、“从一般到特殊”等数学思想的应用能力;
(4)感受二项式定理体现出的数学的内在和谐、对称美,了解相关数学史内容.
项的形式:
a2
ab
ba
b2
思考: 同类项的个数?
2个(a+b)都不选b得到的,因此a2出现的次数相当于从2个(a+b)中取0个b(即都取a)的组合数 ,即a2只有1个;
由1个(a+b)中选a,另1个(a+b)中选b得到的.由于b选定后,a的选法也随之确定,因此,ab出现的次数相当于从2个(a+b)中取1个b的组合数 ,即ab共有2个.
由2个(a+b)中都选b得到的.因此,b2出现的次数相当于从2个(a+b)中取2个b的组合数 ,即b2只有1个.
问题1:观察以上展开式,分析其运算过程,你能发现有什么规律?
a3
问题1:观察以上展开式,分析其运算过程,你能发现有什么规律?
a2b
a2b
a2b
问题1:观察以上展开式,分析其运算过程,你能发现有什么规律?
ab2
ab2
ab2
问题1:观察以上展开式,分析其运算过程,你能发现有什么规律?
b3
展开式共有:
项的形式:
思考: 同类项的个数?
a4
a3b
ab3
b4
a2b2
问题2:你能写出(a+b)4的展开式吗?
证明:
(项的结构)
问题3:写出(a+b)n的展开式?
证明:
(项的系数)
问题3:写出(a+b)n的展开式?
(1)展开式共有 项.
(2)各项的次数都等于二项式的次数n;
字母a按降幂排列,次数由n递减到0;
字母b按升幂排列,次数由0递增到n.
(4)二项展开式中,系数 叫作二项式系数,即
n+1
注意:
二项式定理
思考:
例1、
求 的展开式.
解:根据二项式定理,
变式1:
求 的展开式.
解:根据二项式定理,
例2:
例2:
解:
(1)
(2)
(3)
解:
求 的展开式中 的系数。
的展开式的通项:
根据题意,得
因此, 的系数是
例3:
课堂小结
1、二项式定理
2、二项展开式的通项
3、二项式系数:
