6.3.2 二项式系数的性质 课件(11张PPT)-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册
文档属性
| 名称 | 6.3.2 二项式系数的性质 课件(11张PPT)-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册 |  | |
| 格式 | pptx | ||
| 文件大小 | 340.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-28 21:29:51 | ||
图片预览




文档简介
6.3.2 二项式系数的性质
1.掌握展开式中二项式系数的对称性、增减性与最大值。
2.学会利用赋值法解决二项式系数和的相关问题.
复习引入
1、二项式定理
2、二项展开式的通项
3、二项式系数:
问题1:计算(a+b)n展开式的二项式系数并填入下表
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0} n
(a+b)n展开式的二项式系数
1
2
3
4
5
6
1
6
15
20
15
6
1
1
5
10
10
5
1
1
4
6
4
1
1
3
3
1
1
2
1
1
1
二项式系数:
1 4 6 4 1
1 1
1 2 1
1 3 3 1
1 5 10 10 5 1
1 6 15 20 15 6 1
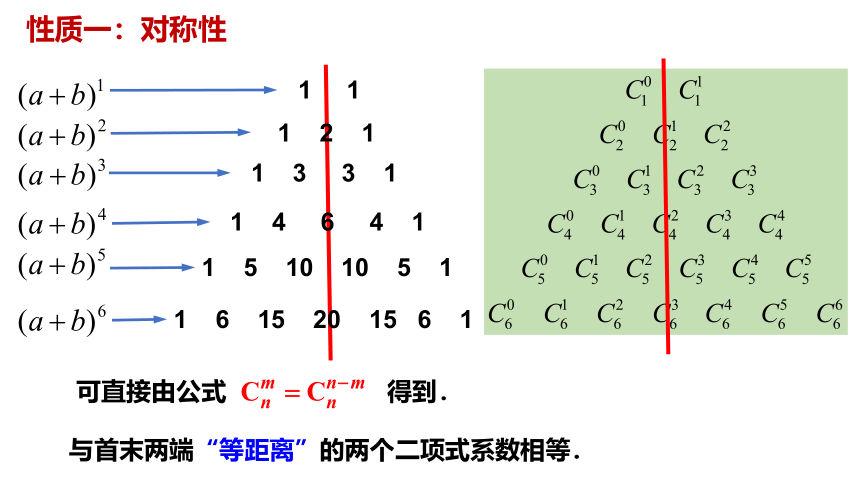
性质一:对称性
与首末两端“等距离”的两个二项式系数相等.
可直接由公式 得到.
因为 展开式的二项式系数依次是:
从函数角度看, 可看成是以k为自变量的函数 ,其定义域是:
对于确定的n,我们还可以画出它的图象,例如,当n=6时,其图象是右图中的7个孤立点.
性质二:增减性与最值
性质二:增减性与最值
∵二项展开式共有n+1项,
∴当n为偶数时,
正中间一项的二项式系数 最大;
当n为奇数时,
中间两项的二项式系数 相等,且同时取得最大值.
性质三:二项式系数之和
(赋值法)
二项式定理:
令x=1:
例3:求证在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
分析:由(a+b)n的展开式可知,
奇数项的二项式系数的和为
偶数项的二项式系数的和为
由于
性质三:二项式系数之和
因此,我们可以通过对a,b适当赋值来得到上述两个系数和。
证明:
即在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和。
例3:求证在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
即
课堂小结
性质一:对称性
与首末两端“等距离”的两个二项式系数相等.
性质二:增减性与最值
当n为偶数时,正中间一项的二项式系数 最大;
当n为奇数时,中间两项的二项式系数 相等,且同时取得最大值.
性质三:二项式系数之和
在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
(赋值法)
1.掌握展开式中二项式系数的对称性、增减性与最大值。
2.学会利用赋值法解决二项式系数和的相关问题.
复习引入
1、二项式定理
2、二项展开式的通项
3、二项式系数:
问题1:计算(a+b)n展开式的二项式系数并填入下表
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0} n
(a+b)n展开式的二项式系数
1
2
3
4
5
6
1
6
15
20
15
6
1
1
5
10
10
5
1
1
4
6
4
1
1
3
3
1
1
2
1
1
1
二项式系数:
1 4 6 4 1
1 1
1 2 1
1 3 3 1
1 5 10 10 5 1
1 6 15 20 15 6 1
性质一:对称性
与首末两端“等距离”的两个二项式系数相等.
可直接由公式 得到.
因为 展开式的二项式系数依次是:
从函数角度看, 可看成是以k为自变量的函数 ,其定义域是:
对于确定的n,我们还可以画出它的图象,例如,当n=6时,其图象是右图中的7个孤立点.
性质二:增减性与最值
性质二:增减性与最值
∵二项展开式共有n+1项,
∴当n为偶数时,
正中间一项的二项式系数 最大;
当n为奇数时,
中间两项的二项式系数 相等,且同时取得最大值.
性质三:二项式系数之和
(赋值法)
二项式定理:
令x=1:
例3:求证在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
分析:由(a+b)n的展开式可知,
奇数项的二项式系数的和为
偶数项的二项式系数的和为
由于
性质三:二项式系数之和
因此,我们可以通过对a,b适当赋值来得到上述两个系数和。
证明:
即在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和。
例3:求证在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
即
课堂小结
性质一:对称性
与首末两端“等距离”的两个二项式系数相等.
性质二:增减性与最值
当n为偶数时,正中间一项的二项式系数 最大;
当n为奇数时,中间两项的二项式系数 相等,且同时取得最大值.
性质三:二项式系数之和
在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
(赋值法)
