17.1.1勾股定理课件(22张)
图片预览






文档简介
17.1.1 勾股定理的认识
第十七章 勾股定理
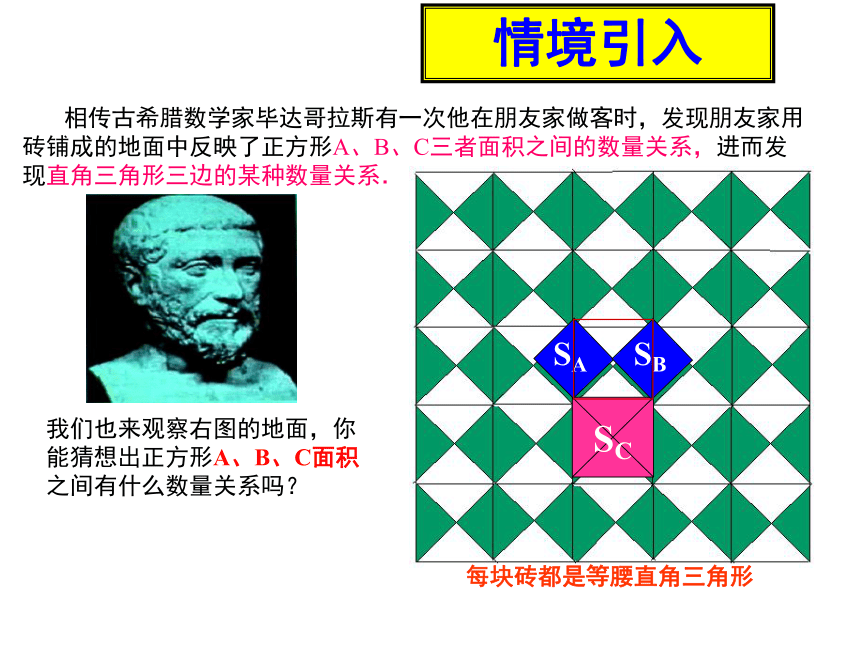
相传古希腊数学家毕达哥拉斯有一次他在朋友家做客时,发现朋友家用砖铺成的地面中反映了正方形A、B、C三者面积之间的数量关系,进而发现直角三角形三边的某种数量关系.
SA
SB
SC
我们也来观察右图的地面,你能猜想出正方形A、B、C面积之间有什么数量关系吗?
每块砖都是等腰直角三角形
情境引入
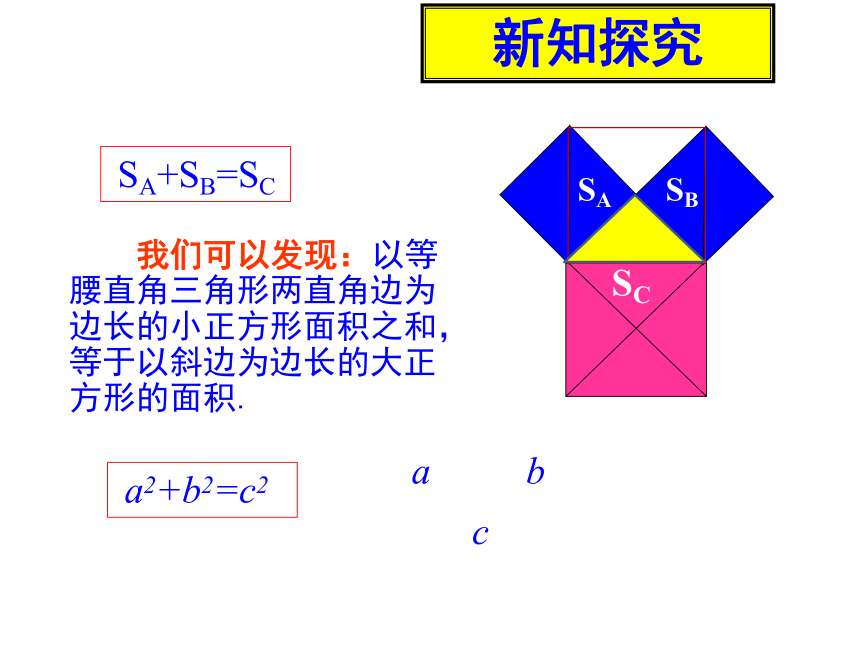
SA+SB=SC
我们可以发现:以等腰直角三角形两直角边为边长的小正方形面积之和,等于以斜边为边长的大正方形的面积.
新知探究
SA
SB
SC
a2+b2=c2
a
b
c
新知探究
新知探究
《周髀算经》
但是,所有的公式定理,不是光靠实验和猜想就能够说明清楚的.特殊的数据永远替代不了一般的规律.
于是当时的数学家们由验证的过程转为了论证的过程. 对一般的直角三角形进行严格的论证.
新知探究
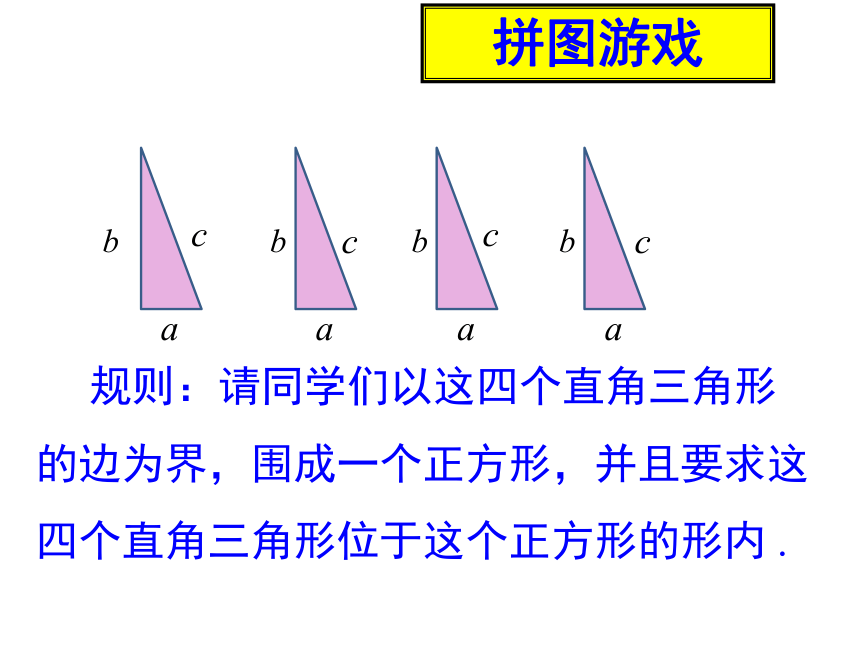
拼图游戏
规则:请同学们以这四个直角三角形的边为界,围成一个正方形,并且要求这四个直角三角形位于这个正方形的形内 .
新知探究
刘徽(约公元225年—295年),山东邹平县人,魏晋期间伟大的数学家,中国古典数学理论的奠基人之一。是中国数学史上一个非常伟大的数学家,他的杰作《九章算术注》和《海岛算经》,是中国最宝贵的数学遗产。
新知探究
加菲尔德是美国政治家、数学家,生于俄亥俄州,1880年加菲尔德当选为第20任总统.他在数学方面的贡献主要是在勾股定理证明方面的新成就,他也是美国历史上唯一一位数学家出身的总统。
勾股定理
新知探究
在直角三角形中,两直角边的平方和等于斜边的平方.
章前图的意义
赵爽弦图
8
6
A
B
C
例1.求图中直角三角形的未知边的长度 .
12
13
A
B
C
典例分析
典例分析
例2. 已知在 中,
(1)若 , , ,则 .
(2)若 , ,则
.
6
或
6
分类讨论
典例分析
例3.一个门框的尺寸如图所示,一块长3 m,宽2.2 m的长方形薄木板能否从门框内通过?为什么?
解:连接AC. 在Rt △ ABC中, ∠ ABC=90 °
∴ AC 2 = AB 2 + BC 2 = 1 2+ 2 2 =5
∴ AC = ≈ 2.24 ( m )
因为AC大于木板的宽度2.2 m,所以木板能从门框内通过 .
思考:
(1)木板横着能否通过?
(2)木板竖着能否通过?
(3)在长方形ABCD中 AB、AC 、BC 哪一条线最长?
本节课我们学到了什么?
一个定理 勾股定理
小结反思
一种思想 以形证数
一次探索 从特殊到一般
一份自豪 作为中国人的民族自豪感
感谢认真的自己!
作业:
1、导学案《课后作业》
2、收集“勾股定理”的证明方法
课后作业
成果展示
1. 已知在 中, ,
(1)若 , ,则 .
(2)若 , ,则 .
(3)若 , ,则 .
11
成果展示
2. 下列说法正确的是( )
A、若 是 的三边,则 .
B、若 是 的三边,则 .
C、若 是 的三边, ,则 .
D、若 是 的三边, ,则 .
D
3. 已知S1=1,S2=3, S3=2,S4=4 , 求S5 、S6 、S7的值.
成果展示
4. 一个直角三角形的两边长分别为 和 ,则第三边的长为 。
或
5.如图,大风将一根木制旗杆吹裂,随时都可能倒下,十分危急.接警后“119”迅速赶到现场,并决定从断裂处将旗杆折断.现在需要划出一个安全警戒区域,那么你能确定这个安全区域的半径至少是多少米吗?
9m
24m
?
成果展示
1.必做题:导学案《课后检测》
2.选做题:
课本第30页“阅读与思考”,了解勾股定理的多种证法.
课后作业
第十七章 勾股定理
相传古希腊数学家毕达哥拉斯有一次他在朋友家做客时,发现朋友家用砖铺成的地面中反映了正方形A、B、C三者面积之间的数量关系,进而发现直角三角形三边的某种数量关系.
SA
SB
SC
我们也来观察右图的地面,你能猜想出正方形A、B、C面积之间有什么数量关系吗?
每块砖都是等腰直角三角形
情境引入
SA+SB=SC
我们可以发现:以等腰直角三角形两直角边为边长的小正方形面积之和,等于以斜边为边长的大正方形的面积.
新知探究
SA
SB
SC
a2+b2=c2
a
b
c
新知探究
新知探究
《周髀算经》
但是,所有的公式定理,不是光靠实验和猜想就能够说明清楚的.特殊的数据永远替代不了一般的规律.
于是当时的数学家们由验证的过程转为了论证的过程. 对一般的直角三角形进行严格的论证.
新知探究
拼图游戏
规则:请同学们以这四个直角三角形的边为界,围成一个正方形,并且要求这四个直角三角形位于这个正方形的形内 .
新知探究
刘徽(约公元225年—295年),山东邹平县人,魏晋期间伟大的数学家,中国古典数学理论的奠基人之一。是中国数学史上一个非常伟大的数学家,他的杰作《九章算术注》和《海岛算经》,是中国最宝贵的数学遗产。
新知探究
加菲尔德是美国政治家、数学家,生于俄亥俄州,1880年加菲尔德当选为第20任总统.他在数学方面的贡献主要是在勾股定理证明方面的新成就,他也是美国历史上唯一一位数学家出身的总统。
勾股定理
新知探究
在直角三角形中,两直角边的平方和等于斜边的平方.
章前图的意义
赵爽弦图
8
6
A
B
C
例1.求图中直角三角形的未知边的长度 .
12
13
A
B
C
典例分析
典例分析
例2. 已知在 中,
(1)若 , , ,则 .
(2)若 , ,则
.
6
或
6
分类讨论
典例分析
例3.一个门框的尺寸如图所示,一块长3 m,宽2.2 m的长方形薄木板能否从门框内通过?为什么?
解:连接AC. 在Rt △ ABC中, ∠ ABC=90 °
∴ AC 2 = AB 2 + BC 2 = 1 2+ 2 2 =5
∴ AC = ≈ 2.24 ( m )
因为AC大于木板的宽度2.2 m,所以木板能从门框内通过 .
思考:
(1)木板横着能否通过?
(2)木板竖着能否通过?
(3)在长方形ABCD中 AB、AC 、BC 哪一条线最长?
本节课我们学到了什么?
一个定理 勾股定理
小结反思
一种思想 以形证数
一次探索 从特殊到一般
一份自豪 作为中国人的民族自豪感
感谢认真的自己!
作业:
1、导学案《课后作业》
2、收集“勾股定理”的证明方法
课后作业
成果展示
1. 已知在 中, ,
(1)若 , ,则 .
(2)若 , ,则 .
(3)若 , ,则 .
11
成果展示
2. 下列说法正确的是( )
A、若 是 的三边,则 .
B、若 是 的三边,则 .
C、若 是 的三边, ,则 .
D、若 是 的三边, ,则 .
D
3. 已知S1=1,S2=3, S3=2,S4=4 , 求S5 、S6 、S7的值.
成果展示
4. 一个直角三角形的两边长分别为 和 ,则第三边的长为 。
或
5.如图,大风将一根木制旗杆吹裂,随时都可能倒下,十分危急.接警后“119”迅速赶到现场,并决定从断裂处将旗杆折断.现在需要划出一个安全警戒区域,那么你能确定这个安全区域的半径至少是多少米吗?
9m
24m
?
成果展示
1.必做题:导学案《课后检测》
2.选做题:
课本第30页“阅读与思考”,了解勾股定理的多种证法.
课后作业
