六年级数学下册试题——圆柱与圆锥 巩固练习 北京版(含解析)
文档属性
| 名称 | 六年级数学下册试题——圆柱与圆锥 巩固练习 北京版(含解析) | 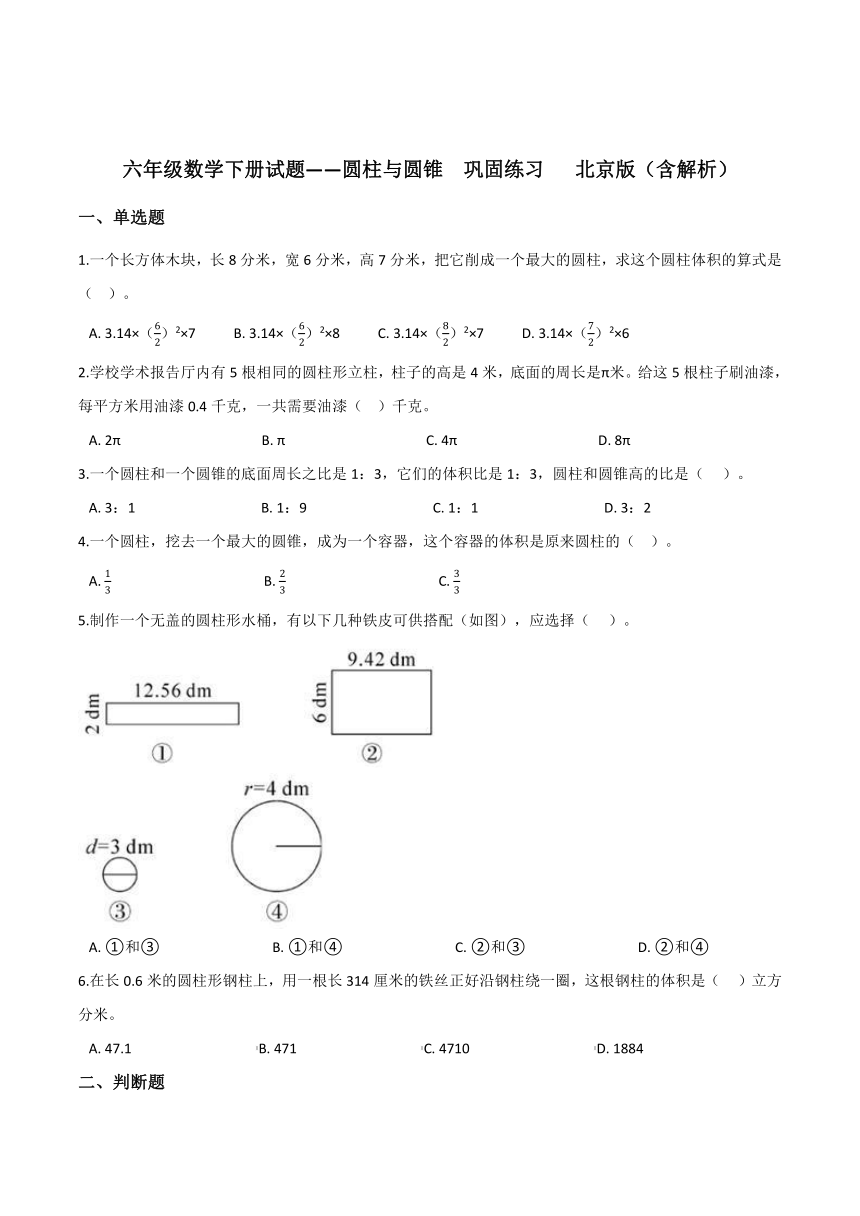 | |
| 格式 | docx | ||
| 文件大小 | 99.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-28 11:56:17 | ||
图片预览



文档简介
六年级数学下册试题——圆柱与圆锥 巩固练习 北京版(含解析)
一、单选题
1.一个长方体木块,长8分米,宽6分米,高7分米,把它削成一个最大的圆柱,求这个圆柱体积的算式是(?? )。
A.?3.14×(62)2×7???????????B.?3.14×(62)2×8???????????C.?3.14×(82)2×7???????????D.?3.14×(72)2×6
2.学校学术报告厅内有5根相同的圆柱形立柱,柱子的高是4米,底面的周长是π米。给这5根柱子刷油漆,每平方米用油漆0.4千克,一共需要油漆(?? )千克。
A.?2π?????????????????????????????????????????B.?π?????????????????????????????????????????C.?4π?????????????????????????????????????????D.?8π
3.一个圆柱和一个圆锥的底面周长之比是1:3,它们的体积比是1:3,圆柱和圆锥高的比是(??? )。
A.?3:1????????????????????????????????????B.?1:9????????????????????????????????????C.?1:1????????????????????????????????????D.?3:2
4.一个圆柱,挖去一个最大的圆锥,成为一个容器,这个容器的体积是原来圆柱的(?? )。
A.?13????????????????????????????????????????????B.?23????????????????????????????????????????????C.?33
5.制作一个无盖的圆柱形水桶,有以下几种铁皮可供搭配(如图),应选择(??? )。
A.?①和③????????????????????????????????B.?①和④????????????????????????????????C.?②和③????????????????????????????????D.?②和④
6.在长0.6米的圆柱形钢柱上,用一根长314厘米的铁丝正好沿钢柱绕一圈,这根钢柱的体积是(??? )立方分米。
A.?47.1????????????????????????????????????B.?471????????????????????????????????????C.?4710????????????????????????????????????D.?1884
二、判断题
7.圆锥的体积一定,它的底面积和高成反比例。(?? )
8.把一个圆柱体削成一个最大的圆锥体削去部分的体积是圆柱体积的 23 。(??? )
9.圆锥的底面半径扩大为原来的2倍,高缩小为原来的一半,体积不变。(?? )
10.一个正方体和一个圆锥体的底面积、高都相等,正方体体积是圆锥体积的3倍.(?? )
11.两个高相等的圆柱,底面半径比是1:2,那么体积比也是1:2。(? ?)
12.一个圆柱的体积是一个圆锥体积的3倍,那么它们一定等底等高.( ??)
三、填空题
13.一个圆柱形铁盒的底面半径是4cm,高是8cm,它的侧面积是________ cm2 ,表面积是________ cm2 ,体积是________ cm3 。
14.一块圆柱形橡皮泥的底面积是20cm2 , 高是15cm。如果把它捏成底面积相同的圆锥,这个圆锥的高是________cm;如果把它捏成同样高度的圆锥,这个圆锥的底面积是________ cm2。
15.把下图所示的长方形铁皮卷成一个高2分米的圆柱形铁桶,铁桶的底面直径大约是________分米,加上底面后,铁桶的表面积约是________平方分米,容积大约是________升。(铁皮的厚度忽略不计)
16.将一根体积为1.2立方米长为6米的圆柱木头锯成同样长的三段儿,它的表面积增加了________。
四、计算题
17.计算下面图形的体积。(单位:cm)
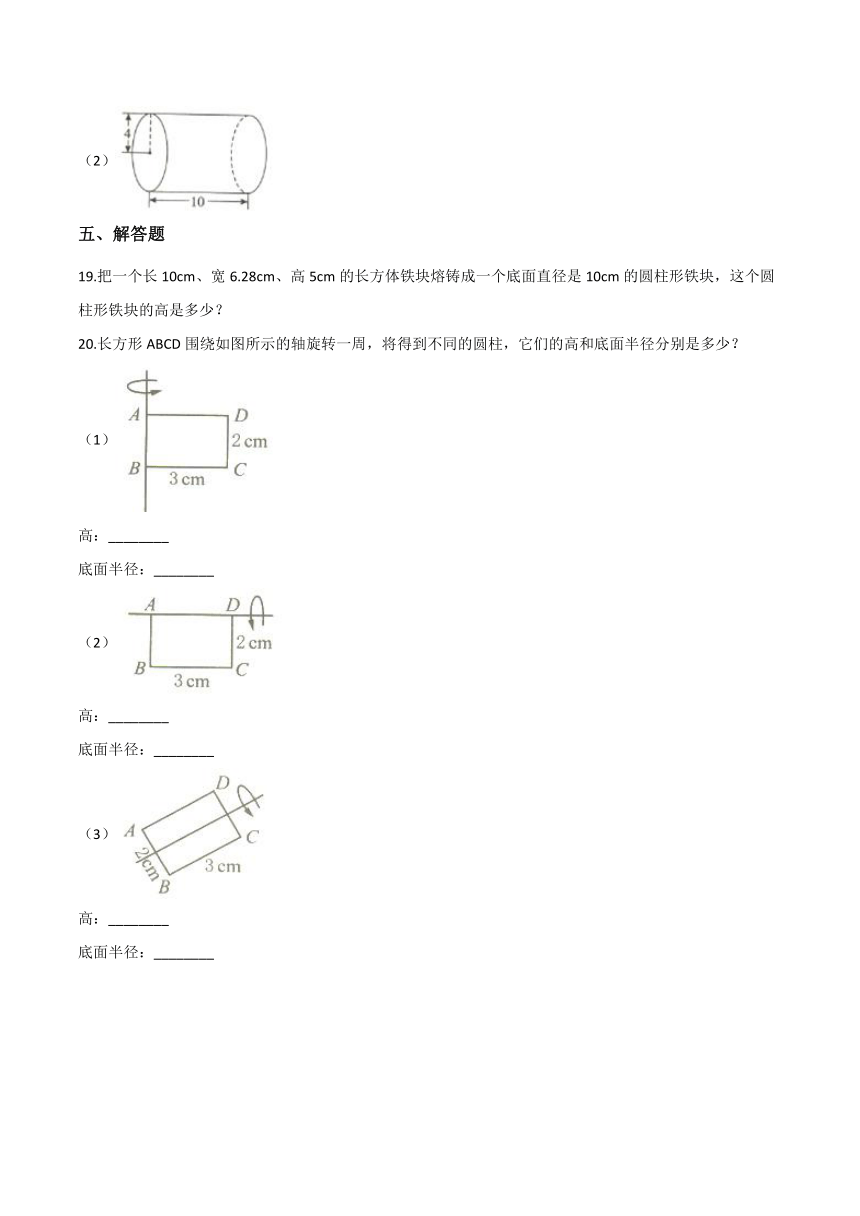
18.计算下列圆柱的表面积。(单位:cm)
(1)
(2)
五、解答题
19.把一个长10cm、宽6.28cm、高5cm的长方体铁块熔铸成一个底面直径是10cm的圆柱形铁块,这个圆柱形铁块的高是多少?
20.长方形ABCD围绕如图所示的轴旋转一周,将得到不同的圆柱,它们的高和底面半径分别是多少?
(1)
高:________
底面半径:________
(2)
高:________
底面半径:________
(3)
高:________
底面半径:________
答案解析部分
一、单选题
1.【答案】 D
【解析】解:求这个圆柱体积的算式是 3.14×(72)2×6。
故答案为:D。
因为要使这个圆柱最大,那么选长方体中最大的面做底面,其中把这个面较短的边的长度座位这个圆柱的底面直径,所以圆柱的体积=π×(直径÷2)2×h。
2.【答案】 D
【解析】解:4π×5×0.4=2π千克,所以一共需要油漆8π千克。
故答案为:D
一共需要油漆的千克数=每根柱子的侧面积×柱子的根数×每平方米用油漆的千克数,其中每根柱子的侧面积=底面周长×π。
3.【答案】 C
【解析】解:因为一个圆柱和一个圆锥的底面周长之比=1:3,
所以圆柱与圆锥的底面半径之比=1:3;
圆柱与圆锥底面面积之比=1:9,
圆柱的底面面积×圆柱的高:圆锥的底面面积×圆锥的高×13=1:3
所以圆柱的高:圆锥的高×3=1:3,
即圆柱的高:圆锥的高=1:1。
故答案为:C。
圆柱的体积=圆柱的底面积×圆柱的高,圆锥的体积=圆锥的底面积×圆锥的高×13 , 圆柱与圆锥的底面周长之比=圆柱与圆锥的底面半径之比,根据圆柱与圆锥的底面面积之比=半径之比的平方,接下来结合圆柱与圆锥的体积比,即可计算出圆柱与圆锥的高的比。
4.【答案】 B
【解析】解:这个容器的体积是原来圆柱的23。
故答案为:B。
把一个圆柱挖去一个最大的圆锥,圆锥的体积是圆柱体积的13 , 剩下部分的体积是圆柱体积的23。
5.【答案】 C
【解析】要做成一个无盖圆柱形水桶,长方形的长应等于底面圆的周长, 图③的周长:3×3.14=9.42cm;图④的周长:4×2×3.14=25.12cm;即③与②可搭配。
故答案为:C。
算出圆的周长,再与之对应长方形的长。
6.【答案】 B
【解析】解:0.6×10=6(分米)
314÷10=31.4(分米)
31.4÷3.14÷2
=10÷2
=5(分米)
3.14×5?×6
=3.14×25×6
=78.5×6
=471(立方分米)
故答案为:B。
先根据周长算出圆柱形钢柱的底面半径,然后根据公式:圆柱体积=底面积×高。
二、判断题
7.【答案】 正确
【解析】解:圆锥的体积=13×底面积×高,所以圆锥的体积一定,它的底面积和高成反比例。
故答案为:正确。
如果xy=k(k为常数,x,y≠0),那么x和y成反比例,然后根据圆锥的体积公式作答即可。
8.【答案】 正确
【解析】解:把一个圆柱体削成一个最大的圆锥体削去部分的体积是圆柱体积的23。原题说法正确。
故答案为:正确。
圆柱的体积=底面积×高,圆锥的体积=底面积×高×13 , 等底等高的圆锥体积是圆柱体积的13;把一个圆柱体削成一个最大的圆锥体,圆锥与圆柱等底等高,所以这个圆锥的体积是圆柱体积的13 , 那么削去的部分就是圆柱体积的23。
9.【答案】 错误
【解析】 假设原来圆锥的底面半径为2,高为4,则变化后的圆锥的底面半径为4,高为2,原来圆锥的体积是:13π×22×4=163π;
现在的圆锥体积是:13π×42×2=323π;
323π÷163π=2,体积扩大2倍,原题说法错误。
故答案为:错误。
根据圆锥的体积公式:V=13πr2h,设原来圆锥的底面半径为2,高为4,则变化后的圆锥的底面半径为4,高为2,分别求出原来和现在圆锥的体积,然后判断体积的变化情况。
10.【答案】 错误
【解析】解:一个正方体和一个圆锥体的底面积、高都相等,正方体体积是圆锥体积的3倍。
故答案为:错误。
正方体的体积=底面积×棱长,圆锥的体积=13×底面积×高,所以当底面积、高都相等时,正方体体积是圆锥体积的3倍。
11.【答案】 错误
【解析】解:两个高相等的圆柱,底面半径比是1:2,那么体积比是12:22=1:4。
故答案为:错误。
两个高相等的圆柱,体积之比是半径平方之比。
12.【答案】 错误
【解析】因为等底等高的圆柱体的体积是圆锥体体积的3倍,所以如果圆柱体积是圆锥体积的3倍,那么它们的底和高度的乘积是相等的,但是底和高不一定相等,原题说法错误。
故答案为:错误。
此题主要考查了圆柱和圆锥的体积关系,等底等高的圆柱体的体积是圆锥体体积的3倍,如果圆柱体积是圆锥体积的3倍,那么它们的底和高的乘积是相等的,但是底和高不一定相等,据此判断。
三、填空题
13.【答案】 200.96;301.44;401.92
【解析】解:3.14×4×2×8
=12.56×2×8
=25.12×8
=200.96(cm?);
3.14×4?×2+200.96
=3.14×16×2+200.96
=50.24×2+200.96
=100.48+200.96
=301.44(cm?);
3.14×4?×8
=3.14×16×8
=50.24×8
=401.92(cm?)。
故答案为:200.96;301.44;401.92。
圆柱的侧面积=π×半径×2×高;圆柱的表面积=底面积×2+侧面积;圆柱的体积=底面积×高。
14.【答案】 45;60
【解析】解:圆锥的高=15÷13=45(cm);
圆锥的底面积=20÷13=60(cm2)。
故答案为:45;60。
圆柱的体积=圆柱的底面积×圆柱的高,圆锥的体积=13×圆锥的底面积×圆锥的高;圆柱与圆锥的体积和底面积相同时,圆柱的高=13×圆锥的高;圆柱与圆锥的体积和高相同时,圆柱的底面积=13×圆锥的底面积,代入数值计算即可。
15.【答案】 2;15.7;6.28
【解析】解:6.28÷3.14=2分米,所以底面直径是2分米;(2÷2)2×3.14+6.28=9.42平方分米,所以铁桶的表面积约是15.7平方分米;(2÷2)2×3.14×2=6.28立方分米=6.28升。
故答案为:2;15.7;6.28。
圆柱的底面直径=底面周长÷π;铁桶的表面积=圆柱的侧面积+圆柱的底面积,其中圆柱的侧面积=圆柱的底面周长×圆柱的高,圆柱的底面积=(直径÷2)2×π;圆柱的体积=(直径÷2)2×π×h。
16.【答案】 0.8平方米
【解析】解:1.2÷6=0.2(平方米)
0.2×4=0.8(平方米)
故答案为:0.8平方米。
锯成同样长的三段儿,它的表面积增加4个底面积;圆柱的体积÷圆柱的长=圆柱的底面积;圆柱的底面积×4=增加的面积。
四、计算题
17.【答案】 3.14×52×4+3.14×52×9× 13 =549.5(cm3)
【解析】图形的体积=上面圆柱的体积+下面圆锥的体积;圆柱的体积=3.14×半径×半径×高;圆锥的体积=3.14×半径×半径×高×13 , 代入数据即可。
18.【答案】 (1)2πr2+2πrh=2×3.14×(20÷2)2+2×3.14×(20÷2)×8=1130.4(cm2)
(2)2πr2+2πrh=2×3.14×42+2×3.14×4×10=351.68(cm2)
【解析】圆柱的表面积=底面积×2+侧面积=2πr2+2πrh,代入数据即可。
五、解答题
19.【答案】 解:10×6.28×5
=62.8×5
=314(cm?);
10÷2=5(cm);
3.14×5?
=3.14×25
=78.5(cm?);
314÷78.5=4(cm)。
答:这个圆柱形铁块的高是4cm。
【解析】圆柱的体积=长方体的体积=长×宽×高;圆柱的高=体积÷底面积;其中,底面积=π×半径?。
20.【答案】 (1)2cm;3cm
(2)3cm;2cm
(3)3cm;1cm
【解析】(1), 高:2cm,底面半径:3cm。
(2), 高3cm,底面半径:2cm;
(3), 高3cm,底面半径:2÷2=1cm。
故答案为:(1)2cm;3cm;(2)3cm;2cm;(3)3cm;1cm。
(1)观察图可知, 将长方形ABCD绕宽AB为轴旋转一周,得到一个圆柱,圆柱的高是长方形的宽,圆柱的底面半径是长方形的长;
(2)观察图可知,将长方形ABCD绕长AD为轴旋转一周,得到一个圆柱,圆柱的高是长方形的长,圆柱的底面半径是长方形的宽;
(3)观察图可知,将长方形ABCD绕两条宽的中点连线为轴旋转一周,得到一个圆柱,圆柱的高是长方形的长,圆柱的底面半径是长方形的宽的一半,据此解答。
一、单选题
1.一个长方体木块,长8分米,宽6分米,高7分米,把它削成一个最大的圆柱,求这个圆柱体积的算式是(?? )。
A.?3.14×(62)2×7???????????B.?3.14×(62)2×8???????????C.?3.14×(82)2×7???????????D.?3.14×(72)2×6
2.学校学术报告厅内有5根相同的圆柱形立柱,柱子的高是4米,底面的周长是π米。给这5根柱子刷油漆,每平方米用油漆0.4千克,一共需要油漆(?? )千克。
A.?2π?????????????????????????????????????????B.?π?????????????????????????????????????????C.?4π?????????????????????????????????????????D.?8π
3.一个圆柱和一个圆锥的底面周长之比是1:3,它们的体积比是1:3,圆柱和圆锥高的比是(??? )。
A.?3:1????????????????????????????????????B.?1:9????????????????????????????????????C.?1:1????????????????????????????????????D.?3:2
4.一个圆柱,挖去一个最大的圆锥,成为一个容器,这个容器的体积是原来圆柱的(?? )。
A.?13????????????????????????????????????????????B.?23????????????????????????????????????????????C.?33
5.制作一个无盖的圆柱形水桶,有以下几种铁皮可供搭配(如图),应选择(??? )。
A.?①和③????????????????????????????????B.?①和④????????????????????????????????C.?②和③????????????????????????????????D.?②和④
6.在长0.6米的圆柱形钢柱上,用一根长314厘米的铁丝正好沿钢柱绕一圈,这根钢柱的体积是(??? )立方分米。
A.?47.1????????????????????????????????????B.?471????????????????????????????????????C.?4710????????????????????????????????????D.?1884
二、判断题
7.圆锥的体积一定,它的底面积和高成反比例。(?? )
8.把一个圆柱体削成一个最大的圆锥体削去部分的体积是圆柱体积的 23 。(??? )
9.圆锥的底面半径扩大为原来的2倍,高缩小为原来的一半,体积不变。(?? )
10.一个正方体和一个圆锥体的底面积、高都相等,正方体体积是圆锥体积的3倍.(?? )
11.两个高相等的圆柱,底面半径比是1:2,那么体积比也是1:2。(? ?)
12.一个圆柱的体积是一个圆锥体积的3倍,那么它们一定等底等高.( ??)
三、填空题
13.一个圆柱形铁盒的底面半径是4cm,高是8cm,它的侧面积是________ cm2 ,表面积是________ cm2 ,体积是________ cm3 。
14.一块圆柱形橡皮泥的底面积是20cm2 , 高是15cm。如果把它捏成底面积相同的圆锥,这个圆锥的高是________cm;如果把它捏成同样高度的圆锥,这个圆锥的底面积是________ cm2。
15.把下图所示的长方形铁皮卷成一个高2分米的圆柱形铁桶,铁桶的底面直径大约是________分米,加上底面后,铁桶的表面积约是________平方分米,容积大约是________升。(铁皮的厚度忽略不计)
16.将一根体积为1.2立方米长为6米的圆柱木头锯成同样长的三段儿,它的表面积增加了________。
四、计算题
17.计算下面图形的体积。(单位:cm)
18.计算下列圆柱的表面积。(单位:cm)
(1)
(2)
五、解答题
19.把一个长10cm、宽6.28cm、高5cm的长方体铁块熔铸成一个底面直径是10cm的圆柱形铁块,这个圆柱形铁块的高是多少?
20.长方形ABCD围绕如图所示的轴旋转一周,将得到不同的圆柱,它们的高和底面半径分别是多少?
(1)
高:________
底面半径:________
(2)
高:________
底面半径:________
(3)
高:________
底面半径:________
答案解析部分
一、单选题
1.【答案】 D
【解析】解:求这个圆柱体积的算式是 3.14×(72)2×6。
故答案为:D。
因为要使这个圆柱最大,那么选长方体中最大的面做底面,其中把这个面较短的边的长度座位这个圆柱的底面直径,所以圆柱的体积=π×(直径÷2)2×h。
2.【答案】 D
【解析】解:4π×5×0.4=2π千克,所以一共需要油漆8π千克。
故答案为:D
一共需要油漆的千克数=每根柱子的侧面积×柱子的根数×每平方米用油漆的千克数,其中每根柱子的侧面积=底面周长×π。
3.【答案】 C
【解析】解:因为一个圆柱和一个圆锥的底面周长之比=1:3,
所以圆柱与圆锥的底面半径之比=1:3;
圆柱与圆锥底面面积之比=1:9,
圆柱的底面面积×圆柱的高:圆锥的底面面积×圆锥的高×13=1:3
所以圆柱的高:圆锥的高×3=1:3,
即圆柱的高:圆锥的高=1:1。
故答案为:C。
圆柱的体积=圆柱的底面积×圆柱的高,圆锥的体积=圆锥的底面积×圆锥的高×13 , 圆柱与圆锥的底面周长之比=圆柱与圆锥的底面半径之比,根据圆柱与圆锥的底面面积之比=半径之比的平方,接下来结合圆柱与圆锥的体积比,即可计算出圆柱与圆锥的高的比。
4.【答案】 B
【解析】解:这个容器的体积是原来圆柱的23。
故答案为:B。
把一个圆柱挖去一个最大的圆锥,圆锥的体积是圆柱体积的13 , 剩下部分的体积是圆柱体积的23。
5.【答案】 C
【解析】要做成一个无盖圆柱形水桶,长方形的长应等于底面圆的周长, 图③的周长:3×3.14=9.42cm;图④的周长:4×2×3.14=25.12cm;即③与②可搭配。
故答案为:C。
算出圆的周长,再与之对应长方形的长。
6.【答案】 B
【解析】解:0.6×10=6(分米)
314÷10=31.4(分米)
31.4÷3.14÷2
=10÷2
=5(分米)
3.14×5?×6
=3.14×25×6
=78.5×6
=471(立方分米)
故答案为:B。
先根据周长算出圆柱形钢柱的底面半径,然后根据公式:圆柱体积=底面积×高。
二、判断题
7.【答案】 正确
【解析】解:圆锥的体积=13×底面积×高,所以圆锥的体积一定,它的底面积和高成反比例。
故答案为:正确。
如果xy=k(k为常数,x,y≠0),那么x和y成反比例,然后根据圆锥的体积公式作答即可。
8.【答案】 正确
【解析】解:把一个圆柱体削成一个最大的圆锥体削去部分的体积是圆柱体积的23。原题说法正确。
故答案为:正确。
圆柱的体积=底面积×高,圆锥的体积=底面积×高×13 , 等底等高的圆锥体积是圆柱体积的13;把一个圆柱体削成一个最大的圆锥体,圆锥与圆柱等底等高,所以这个圆锥的体积是圆柱体积的13 , 那么削去的部分就是圆柱体积的23。
9.【答案】 错误
【解析】 假设原来圆锥的底面半径为2,高为4,则变化后的圆锥的底面半径为4,高为2,原来圆锥的体积是:13π×22×4=163π;
现在的圆锥体积是:13π×42×2=323π;
323π÷163π=2,体积扩大2倍,原题说法错误。
故答案为:错误。
根据圆锥的体积公式:V=13πr2h,设原来圆锥的底面半径为2,高为4,则变化后的圆锥的底面半径为4,高为2,分别求出原来和现在圆锥的体积,然后判断体积的变化情况。
10.【答案】 错误
【解析】解:一个正方体和一个圆锥体的底面积、高都相等,正方体体积是圆锥体积的3倍。
故答案为:错误。
正方体的体积=底面积×棱长,圆锥的体积=13×底面积×高,所以当底面积、高都相等时,正方体体积是圆锥体积的3倍。
11.【答案】 错误
【解析】解:两个高相等的圆柱,底面半径比是1:2,那么体积比是12:22=1:4。
故答案为:错误。
两个高相等的圆柱,体积之比是半径平方之比。
12.【答案】 错误
【解析】因为等底等高的圆柱体的体积是圆锥体体积的3倍,所以如果圆柱体积是圆锥体积的3倍,那么它们的底和高度的乘积是相等的,但是底和高不一定相等,原题说法错误。
故答案为:错误。
此题主要考查了圆柱和圆锥的体积关系,等底等高的圆柱体的体积是圆锥体体积的3倍,如果圆柱体积是圆锥体积的3倍,那么它们的底和高的乘积是相等的,但是底和高不一定相等,据此判断。
三、填空题
13.【答案】 200.96;301.44;401.92
【解析】解:3.14×4×2×8
=12.56×2×8
=25.12×8
=200.96(cm?);
3.14×4?×2+200.96
=3.14×16×2+200.96
=50.24×2+200.96
=100.48+200.96
=301.44(cm?);
3.14×4?×8
=3.14×16×8
=50.24×8
=401.92(cm?)。
故答案为:200.96;301.44;401.92。
圆柱的侧面积=π×半径×2×高;圆柱的表面积=底面积×2+侧面积;圆柱的体积=底面积×高。
14.【答案】 45;60
【解析】解:圆锥的高=15÷13=45(cm);
圆锥的底面积=20÷13=60(cm2)。
故答案为:45;60。
圆柱的体积=圆柱的底面积×圆柱的高,圆锥的体积=13×圆锥的底面积×圆锥的高;圆柱与圆锥的体积和底面积相同时,圆柱的高=13×圆锥的高;圆柱与圆锥的体积和高相同时,圆柱的底面积=13×圆锥的底面积,代入数值计算即可。
15.【答案】 2;15.7;6.28
【解析】解:6.28÷3.14=2分米,所以底面直径是2分米;(2÷2)2×3.14+6.28=9.42平方分米,所以铁桶的表面积约是15.7平方分米;(2÷2)2×3.14×2=6.28立方分米=6.28升。
故答案为:2;15.7;6.28。
圆柱的底面直径=底面周长÷π;铁桶的表面积=圆柱的侧面积+圆柱的底面积,其中圆柱的侧面积=圆柱的底面周长×圆柱的高,圆柱的底面积=(直径÷2)2×π;圆柱的体积=(直径÷2)2×π×h。
16.【答案】 0.8平方米
【解析】解:1.2÷6=0.2(平方米)
0.2×4=0.8(平方米)
故答案为:0.8平方米。
锯成同样长的三段儿,它的表面积增加4个底面积;圆柱的体积÷圆柱的长=圆柱的底面积;圆柱的底面积×4=增加的面积。
四、计算题
17.【答案】 3.14×52×4+3.14×52×9× 13 =549.5(cm3)
【解析】图形的体积=上面圆柱的体积+下面圆锥的体积;圆柱的体积=3.14×半径×半径×高;圆锥的体积=3.14×半径×半径×高×13 , 代入数据即可。
18.【答案】 (1)2πr2+2πrh=2×3.14×(20÷2)2+2×3.14×(20÷2)×8=1130.4(cm2)
(2)2πr2+2πrh=2×3.14×42+2×3.14×4×10=351.68(cm2)
【解析】圆柱的表面积=底面积×2+侧面积=2πr2+2πrh,代入数据即可。
五、解答题
19.【答案】 解:10×6.28×5
=62.8×5
=314(cm?);
10÷2=5(cm);
3.14×5?
=3.14×25
=78.5(cm?);
314÷78.5=4(cm)。
答:这个圆柱形铁块的高是4cm。
【解析】圆柱的体积=长方体的体积=长×宽×高;圆柱的高=体积÷底面积;其中,底面积=π×半径?。
20.【答案】 (1)2cm;3cm
(2)3cm;2cm
(3)3cm;1cm
【解析】(1), 高:2cm,底面半径:3cm。
(2), 高3cm,底面半径:2cm;
(3), 高3cm,底面半径:2÷2=1cm。
故答案为:(1)2cm;3cm;(2)3cm;2cm;(3)3cm;1cm。
(1)观察图可知, 将长方形ABCD绕宽AB为轴旋转一周,得到一个圆柱,圆柱的高是长方形的宽,圆柱的底面半径是长方形的长;
(2)观察图可知,将长方形ABCD绕长AD为轴旋转一周,得到一个圆柱,圆柱的高是长方形的长,圆柱的底面半径是长方形的宽;
(3)观察图可知,将长方形ABCD绕两条宽的中点连线为轴旋转一周,得到一个圆柱,圆柱的高是长方形的长,圆柱的底面半径是长方形的宽的一半,据此解答。
