第18章平行四边形 单元培优训练题(Word版 含解析)
文档属性
| 名称 | 第18章平行四边形 单元培优训练题(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 628.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 22:31:14 | ||
图片预览

文档简介
第18章平行四边形 单元培优训练题
1.如图,四边形ABCD是平行四边形,下列说法不正确的是( )
A.当AC=BD时,四边形ABCD是矩形
B.当AB=BC时,四边形ABCD是菱形
C.当AC平分∠BAD时,四边形ABCD是菱形
D.当∠DAB=90°时,四边形ABCD是正方形
2.如图,矩形ABCD中,BC>AB,对角线AC、BD交于O点,且AC=10,过B点作BE⊥AC于E点,若BE=4,则AD的长等于( )
A.8 B.10 C.3 D.4
3.如图,在平行四边形ABCD中,AD=6,点E在边AD上,点F在BC的延长线上,且满足BF=BE=8,过点C作CE的垂线交BE于点G,若CE恰好平分∠BEF,则BG的长为( )
A.2 B.3 C.4 D.2
4.如图,在正方形ABCD中,M为边BC上的一点,MN⊥BC交BD于点N,连接AM交BD于点E,F为DN中点,连接AF.有下列说法:①BN=BM;②∠BAF=∠AEF;③BE2+DF2=EF2;④AB﹣MN=DF.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
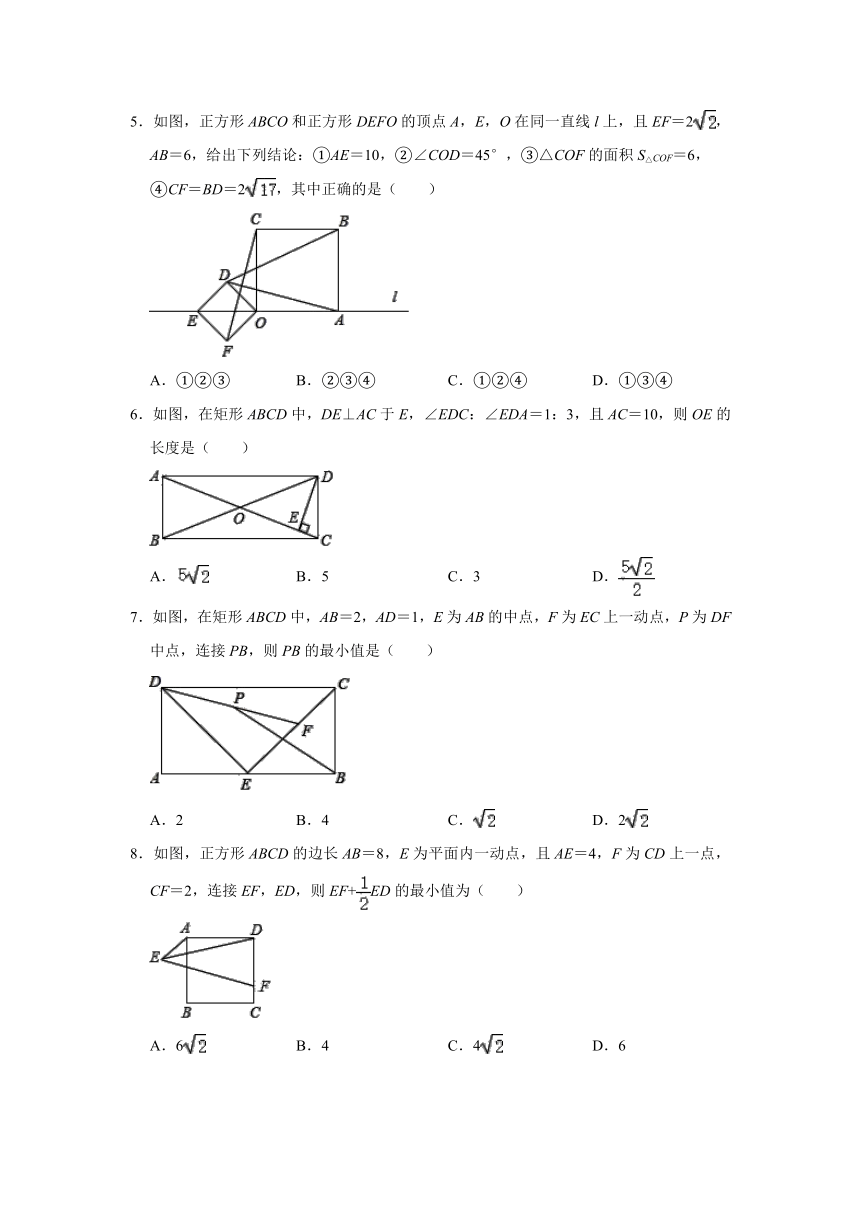
5.如图,正方形ABCO和正方形DEFO的顶点A,E,O在同一直线l上,且EF=2,AB=6,给出下列结论:①AE=10,②∠COD=45°,③△COF的面积S△COF=6,
④CF=BD=2,其中正确的是( )
A.①②③ B.②③④ C.①②④ D.①③④
6.如图,在矩形ABCD中,DE⊥AC于E,∠EDC:∠EDA=1:3,且AC=10,则OE的长度是( )
A. B.5 C.3 D.
7.如图,在矩形ABCD中,AB=2,AD=1,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值是( )
A.2 B.4 C. D.2
8.如图,正方形ABCD的边长AB=8,E为平面内一动点,且AE=4,F为CD上一点,CF=2,连接EF,ED,则EF+ED的最小值为( )
A.6 B.4 C.4 D.6
9.如图,AB⊥AF,EF⊥AF,BE与AF交于点C,点D是BC的中点,∠AEB=2∠B.若BC=8,EF=,则AF的长是( )
A. B. C.3 D.5
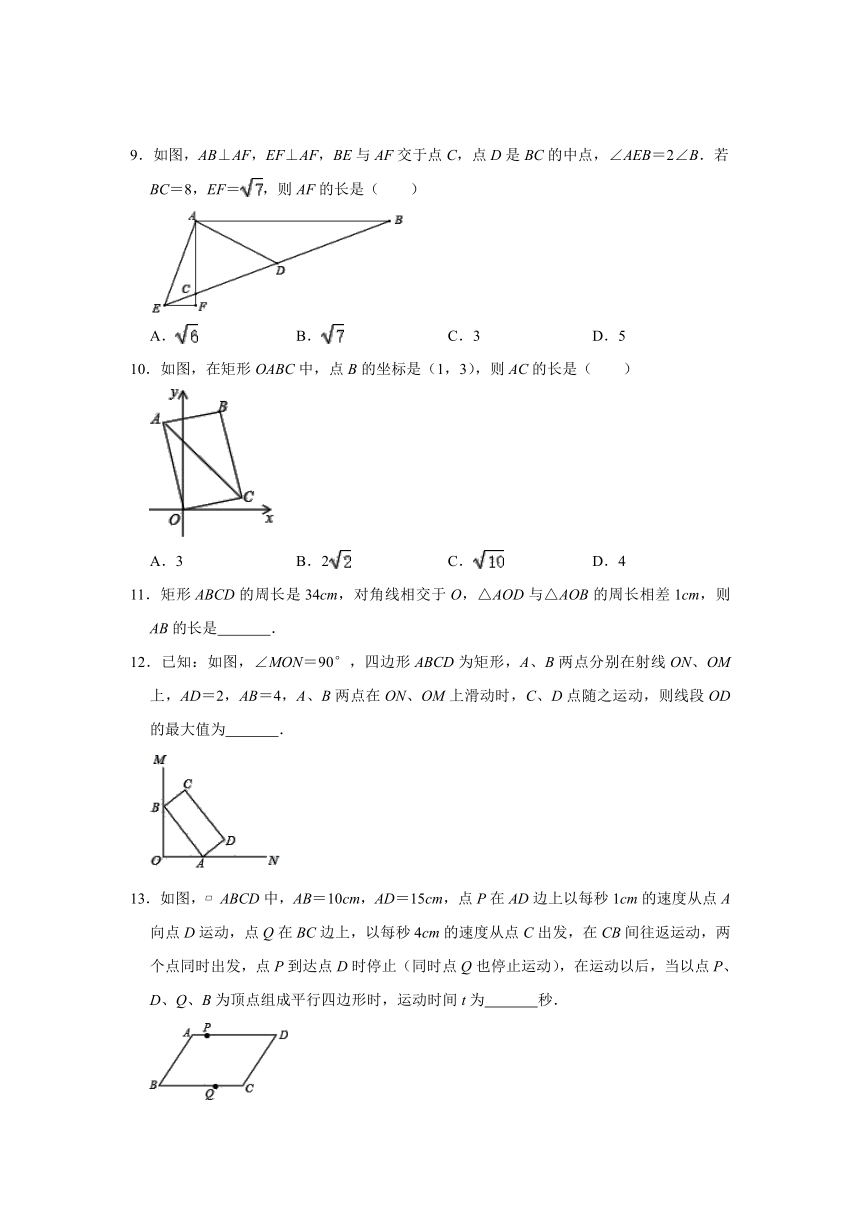
10.如图,在矩形OABC中,点B的坐标是(1,3),则AC的长是( )
A.3 B.2 C. D.4
11.矩形ABCD的周长是34cm,对角线相交于O,△AOD与△AOB的周长相差1cm,则AB的长是 .
12.已知:如图,∠MON=90°,四边形ABCD为矩形,A、B两点分别在射线ON、OM上,AD=2,AB=4,A、B两点在ON、OM上滑动时,C、D点随之运动,则线段OD的最大值为 .
13.如图,?ABCD中,AB=10cm,AD=15cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,点P到达点D时停止(同时点Q也停止运动),在运动以后,当以点P、D、Q、B为顶点组成平行四边形时,运动时间t为 秒.
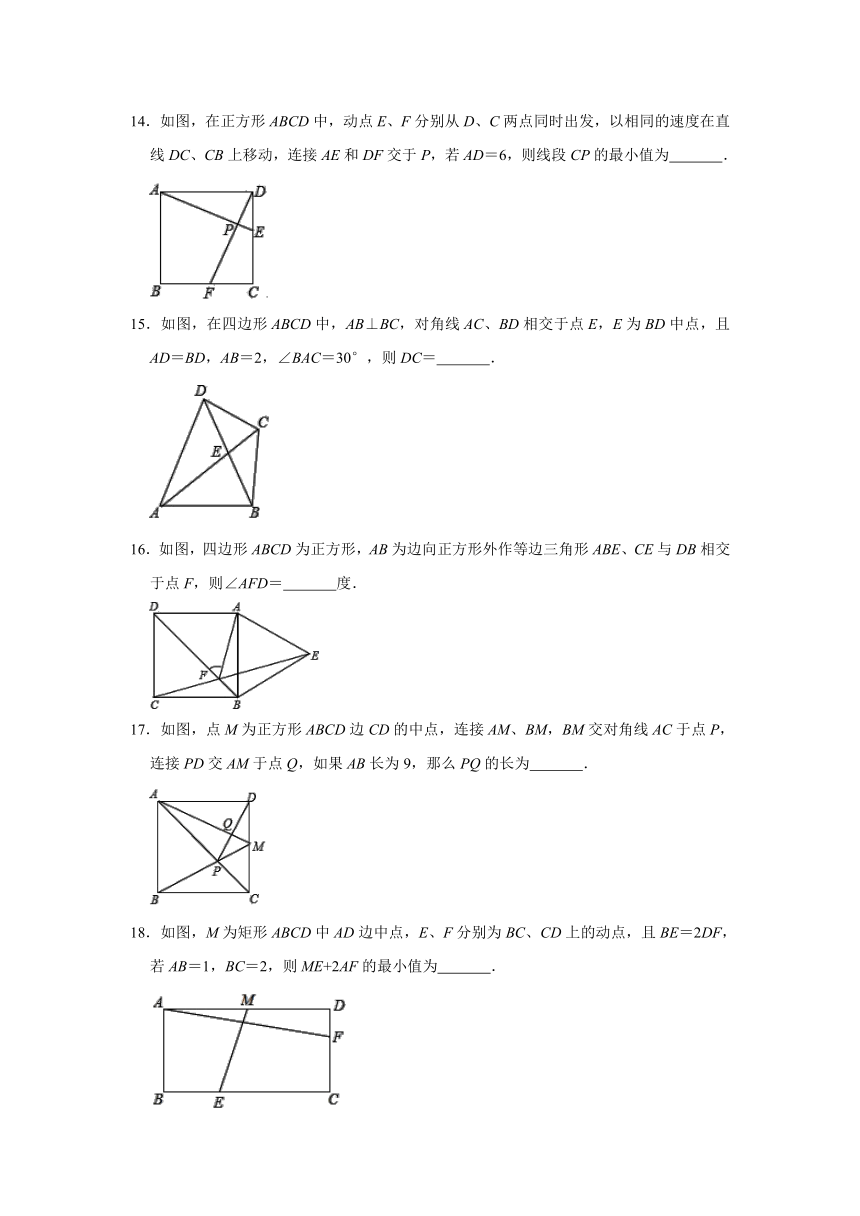
14.如图,在正方形ABCD中,动点E、F分别从D、C两点同时出发,以相同的速度在直线DC、CB上移动,连接AE和DF交于P,若AD=6,则线段CP的最小值为 .
15.如图,在四边形ABCD中,AB⊥BC,对角线AC、BD相交于点E,E为BD中点,且AD=BD,AB=2,∠BAC=30°,则DC= .
16.如图,四边形ABCD为正方形,AB为边向正方形外作等边三角形ABE、CE与DB相交于点F,则∠AFD= 度.
17.如图,点M为正方形ABCD边CD的中点,连接AM、BM,BM交对角线AC于点P,连接PD交AM于点Q,如果AB长为9,那么PQ的长为 .
18.如图,M为矩形ABCD中AD边中点,E、F分别为BC、CD上的动点,且BE=2DF,若AB=1,BC=2,则ME+2AF的最小值为 .
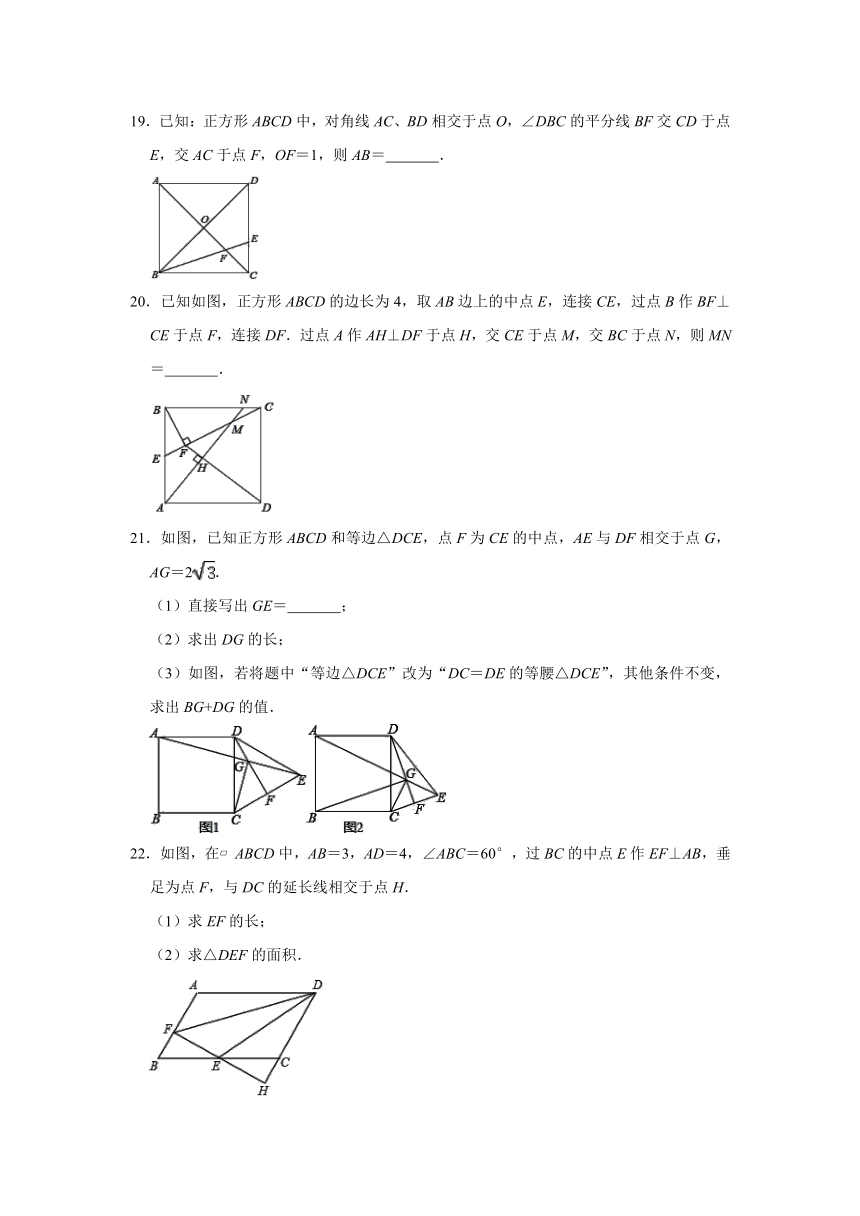
19.已知:正方形ABCD中,对角线AC、BD相交于点O,∠DBC的平分线BF交CD于点E,交AC于点F,OF=1,则AB= .
20.已知如图,正方形ABCD的边长为4,取AB边上的中点E,连接CE,过点B作BF⊥CE于点F,连接DF.过点A作AH⊥DF于点H,交CE于点M,交BC于点N,则MN= .
21.如图,已知正方形ABCD和等边△DCE,点F为CE的中点,AE与DF相交于点G,AG=2.
(1)直接写出GE= ;
(2)求出DG的长;
(3)如图,若将题中“等边△DCE”改为“DC=DE的等腰△DCE”,其他条件不变,求出BG+DG的值.
22.如图,在?ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H.
(1)求EF的长;
(2)求△DEF的面积.
23.在平行四边形ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
(1)如图①,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图②,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.
24.如图1,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°
(1)求证:AG=FG;
(2)如图2延长FC、AE交于点M,连接DF、BM,若C为FM中点,BM=10,求FD的长.
25.如图,四边形ABCD是正方形,E、F分别是AB和BC延长线上的点,且AE=CF.
(1)求证:△ADE≌△CDF;
(2)连接EF,若AB=3,AE=1,求EF的长.
26.如图1,菱形ABCD中,∠BAD=60°,点E、F分别是边AB、AD上两个动点,满足AE=DF,连接BF与DE相交于点G.
(1)如图2,连接BD,求∠BGD的度数;
(2)如图3,作CH⊥BG于H点,求证:2GH=DG+BG.
27.如图,平行四边形ABCD中,AC与BD相交于点O,AB=AC,延长BC到点E,使CE=BC,连接AE,分别交BD、CD于点F、G.
(1)求证:△ADB≌△CEA;
(2)若BD=9,求AF的长.
28.已知四边形ABCD是正方形,点P,Q在直线BC上,且AP∥DQ,过点Q作QO⊥BD,垂足为点O,连接OA,OP.
(1)如图,点P在线段BC上,
①求证:四边形APQD是平行四边形;
②判断OA,OP之间的数量关系和位置关系,并加以证明;
(2)若正方形ABCD的边长为2,直接写出BP=1时,△OBP的面积.
参考答案
1.解:①由矩形的判定“对角线相等的平行四边形是矩形”可知,A正确;
②由菱形的判定“有一组邻边相等的平行四边形是菱形”可知,B正确;
③∵AC平分∠BAD,
∴∠DAC=∠CAB,
∵CD∥AB,
∴∠DCA=∠CAB,
∴∠DAC=∠DCA,
∴DA=DC,
∴平行四边形ABCD是菱形,故C正确;
④在平行四边形ABCD中,
∵∠DAB=90°,
∴平行四边形ABCD是矩形,而不能判定其是正方形,故D错误;
故选:D.
2.解:∵四边形ABCD是矩形,
∴∠BAD=90°,设AD=BC=a,AB=DC=b,
∵AC=10,BE⊥AC,BE=4,
∴a2+b2=102,
又∵S矩形ABCD=2S△ABC
∴ab=2××10×4=40,
∵BC>AB,
解得:a=4,b=2,
即AD=4,
故选:D.
3.解:如图,延长EF,GC两条线相交于点H,过点G作GP∥EF交BC于点P,
∵四边形ABCD是平行四边形,
∴BC=AD=6,
∵BF=BE=8,
∴CF=BF﹣BC=2,
∵CE平分∠BEF,
∴∠GEC=∠HEC,
∵CE⊥GC,
∴∠ECG=∠ECH=90°,
在△ECG和△ECH中,
,
∴△ECG≌△ECH(ASA),
∴CG=CH,
∵GP∥EF,
∴∠PGC=∠FHC,
在△PCG和△FCH中,
,
∴△PCG≌△FCH(ASA),
∴CP=CF=2,
∴BP=BF﹣PF=8﹣4=4,
∵BF=BE,
∴∠BEF=∠BFE,
∵GP∥EF,
∴∠BGP=∠BEF,∠BPG=∠BFE,
∴∠BGP=∠BPG,
∴BG=BP=4.
故选:C.
4.解:①∵四边形ABCD是正方形,
∴∠DBC=45°,
∵MN⊥BC,
∴∠BMN=90°,
∴△MNB是等腰直角三角形,
∴BM=MN,
∴BN=BM;
故①正确;
②过F作GH⊥BC于H,交AD于G,连接FM、FC,
∵AD∥BC,
∴GH⊥AD,
∵四边形ABCD是正方形,
∴AD=BC,∠ADF=∠CDF=45°,
∵DF=DF,
∴△ADF≌△CDF,
∴AF=CF,
∵∠FDG=45°,∠FGD=90°,
∴△FGD是等腰直角三角形,
∴FG=DG=CH,
∴Rt△AFG≌Rt△FCH(HL),
∴∠FAG=∠CFH,
∵MN∥FH∥DC,F是DN的中点,
∴MH=CH,
∵FH⊥CM,
∴FM=FC,
∴∠MFH=∠CFH=∠FAG,
∵∠AGF=∠FAG+∠AFG=∠MFH+∠AFG=90°,
∴∠AFM=90°,
∵AF=FC=FM,
∴△AFM是等腰直角三角形,
∴∠MAF=45°,
∵∠BAF=∠BAM+∠MAF=∠BAM+45°,
∠AEF=∠BAM+∠ABE=∠BAM+45°,
∴∠BAF=∠AEF;
故②正确;
③∵AD=AB,∠DAB=90°,
∴将△AFD绕点A顺时针旋转90°至△ABF',
∴△AFD≌△AF'B,
∴DF=BF',∠ABF'=∠ADF=45°,AF=AF',
∴∠EBF'=45°+45°=90°,
∴EF'2=BF'2+BE2=DF2+BE2,
∵∠F'AE=∠F'AB+∠BAE=∠FAD+∠BAE=45°=∠EAF,AN=AN,
∴△F'AE≌△FAE,
∴EF=EF',
∴EF2=BE2+DF2;
故③正确;
④过F作FR⊥CD,垂足为P,使FP=PR,连接DR、RC,
∵∠FDP=45°,
∴∠DFP=45°,
∴FP=PD=PR,
∴∠FDR=90°,△FDR是等腰直角三角形,
∴FR=DF,
∵FR=2FP,CM=2CH=2FP,
∴FR=CM,
∵AB=CB,BM=MN,
∴CM=BC﹣BM=AB﹣BM=AB﹣MN,
∴AB﹣MN=DF,
故④正确;
本题正确的结论有:①②③④,4个故选:D.
5.解:①∵EF=2,
∴OE=4,
∵AO=AB=6,
∴AE=AO+OE=6+4=10,故正确;
②∵∠AOC=90°,∠DOE=45°,
∴∠COD=180°﹣∠AOC﹣∠DOE=45°,故正确;
③作FG⊥CO交CO的延长线于G,
则FG=2,
∴△COF的面积S△COF=×6×2=6,故正确;
④作DH⊥AB于H,
CF==2,
BH=6﹣2=4,
DH=6+2=8,
BD==4,故错误.故选:A.
6.解:∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD=10,OA=OC=AC=5,OB=OD=BD=5,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠EDC:∠EDA=1:3,∠EDC+∠EDA=90°,
∴∠EDC=22.5°,∠EDA=67.5°,
∵DE⊥AC,
∴∠DEC=90°,
∴∠DCE=90°﹣∠EDC=67.5°,
∴∠ODC=∠OCD=67.5°,
∴∠ODC+∠OCD+∠DOC=180°,
∴∠COD=45°,
∴OE=DE,
∵OE2+DE2=OD2,
∴(2DE)2=OD2=25,
∴DE=,故选:D.
7.解:如图:
当点F与点C重合时,点P在P1处,CP1=DP1,
当点F与点E重合时,点P在P2处,EP2=DP2,
∴P1P2∥CE且P1P2=CE.
当点F在EC上除点C、E的位置处时,有DP=FP.
由中位线定理可知:P1P∥CE且P1P=CF.
∴点P的运动轨迹是线段P1P2,
∴当BP⊥P1P2时,PB取得最小值.
∵矩形ABCD中,AB=2,AD=1,E为AB的中点,
∴△CBE、△ADE、△BCP1为等腰直角三角形,CP1=1.
∴∠ADE=∠CDE=∠CP1B=45°,∠DEC=90°.
∴∠DP2P1=90°.
∴∠DP1P2=45°.
∴∠P2P1B=90°,即BP1⊥P1P2,
∴BP的最小值为BP1的长.
在等腰直角BCP1中,CP1=BC=1.
∴BP1=.
∴PB的最小值是.故选:C.
8.解:如图,当点E运动到点E′时,EF+ED的值最小,最小值为EF+DE',
在AD边上取AH=2,
∵AE′=AE=4,
∴=2,
∵AD=8,
∴=2,
∴,
∵∠DAE′=∠E′AH,
∴△DAE′∽△E′AH,
∴=2,
∴E′H=DE',
∴EF+ED=EF+E′D=EF+E′H=HF,
∴EF+ED的最小值为HF的值,
∵DH=AD﹣AH=6,
DF=DC﹣CF=6,
在Rt△DHF中,根据勾股定理,得
HF=,故选:A.
9.解:∵AB⊥AF,
∴∠FAB=90°,
∵点D是BC的中点,
∴AD=BD=BC,
∴∠DAB=∠B,
∴∠ADE=∠B+∠BAD=2∠B,
∵∠AEB=2∠B,
∴∠AED=∠ADE,
∴AE=AD,
∵BC=8,
∴AE=AD=4,
∵EF=,EF⊥AF,
∴AF===3,
故选:C.
10.解:
连接OB,过B作BM⊥x轴于M,
∵点B的坐标是(1,3),
∴OM=1,BM=3,由勾股定理得:OB==,
∵四边形OABC是矩形,
∴AC=OB,
∴AC=,
故选:C.
11.解:由图易得:OB=OD,那么△AOD与△AOB的周长相差1cm其实就是AD与AB相差1cm
当AD比AB长1cm时,AD+AB=AB+1+AB=17,AB=8;
当AD比AB短1cm时,AD+AB=AB﹣1+AB=17,AB=9.
因此AB的长为8或9cm.故AB的长为8或9cm.
12.解:如图,取AB的中点E,连接OE、DE、OD,
∵OD<OE+DE,
∴当O、D、E三点共线时,点D到点O的距离最大,
此时,∵AB=4,BC=2,
∴OE=AE=AB=2,
DE==2,
∴OD的最大值为:2+2.
故答案为:2+2.
13.解:设经过t秒,以点P、D、Q、B为顶点组成平行四边形,
∵P在AD上运动,
∴t≤,即t≤15,
∵以点P、D、Q、B为顶点组成平行四边形,
∴DP=BQ,
分为以下情况:①点Q的运动路线是C﹣B﹣C,方程为4t﹣15=15﹣t,
解得:t=6;
②点Q的运动路线是C﹣B﹣C﹣B,方程为15﹣(4t﹣30)=15﹣t,
解得:t=10;
③点Q的运动路线是C﹣B﹣C﹣B﹣C,方程为4t﹣45=15﹣t,
解得:t=12;
故答案为:6或10或12.
14.解:由题意得:AD=CD,DE=FC,∠ADC=∠DCF=90°,
∴△DCF≌△ADE(SAS),∴∠DAE=∠FDC,
∴∠APD=90°,即:相当于点P始终在以AD为直径的圆上,
取AD的中点Q,当Q、P、C三点共线时,PC最小,
PC=CQ﹣PQ=﹣3=3﹣3.
故:答案是3﹣3.
15.解:如图,在EA上取一点K,使得EK=CE,连接DK,BK,延长DK交AB于H.
∵DE=EB,CE=EK,
∴四边形BCDK是平行四边形,
∴CD=BK,DK∥BC,
∵BC⊥AB,
∴DH⊥AB,
∵DA=DB,
∴AH=HB=1,
∴KA=KB=CD,
在Rt△AKH中,AK=AH÷cos30°=,
∴CD=,
故答案为.
16.解:∵∠CBA=90°,∠ABE=60°,
∴∠CBE=150°,
∵四边形ABCD为正方形,三角形ABE为等边三角形
∴BC=BE,
∴∠BEC=15°,
∵∠FBE=∠DBA+∠ABE=105°,
∴∠BFE=60°,
在△CBF和△ABF中,
,
∴△CBF≌△ABF(SAS),
∴∠BAF=∠BCE=15°,
又∠ABF=45°,且∠AFD为△AFB的外角,
∴∠AFD=∠ABF+∠FAB=15°+45°=60°.
故答案为60.
17.解:如图,延长P交BC于H.
∵四边形ABCD是正方形,
∴AB=CD=AD=BC=9,AB∥CD,AD∥BC,
∵DM=CM=4.5,
∴PC:PA=CM:AB=1:2,CH:AD=CP:PA=1:2,
∴AD=2CH,
∴CB=2CH,
∴CH=BH=4.5,
∵AD=CD,∠ADM=∠DCH,DM=CH,
∴△ADM≌△DCH,
∴∠DAM=∠CDH,
∵∠DAM+∠AMD=90°,
∴∠CDH+∠DMA=90°,
∴∠DQM=90°,
∵DH==,
∵DP{PH=AD:CH=2:1,
∴DP=DH=3,
∵AM=DH=,
∴DQ==,
∴PQ=PD﹣DQ=,
故答案为.
18.解:如图,过点M作MH⊥BC于H.设DF=x,则BE=2x.
∵四边形ABCD是矩形,
∴∠BAD=∠B=∠D=90°,
∵MH⊥BC,
∴∠MHB=90°,
∴四边形ABHM是矩形,
∴AM=DM=BH=1,AB=MH=1,
∴EH=1﹣2x,
∴ME+2AF=+2=+,
欲求ME+2AF的最小值,相当于在x轴上找一点Q(2x,0),使得点Q到J(0,4),和K(1,1)的距离之和最小(如下图),
作点J关于x轴的对称点J′,连接KJ′交x轴于Q,连接JQ,此时JQ+QK的值最小,最小值=KJ′,
∵J′(0,﹣4),K(1,1),
∴KJ′==,
∴ME+2AF的最小值为,
故答案为.
19.解:如图作FH∥BC交BD于点H.
∵四边形ABCD是正方形,
∴∠OBC=∠OCB=45°,OB=OC,∠BOC=90°
∵FH∥BC,
∴∠OHF=∠OBC,∠OFH=∠OCB,
∴∠OHF=∠OFH,
∴OH=OF=1,FH==,
∵BF平分∠OBC,
∴∠HBF=∠FBC=∠BFH,
∴BH=FH=,
∴OB=OC=1+,
∴BC=OB=2+.
故答案为2+.
20.解:如图,延长DF交AB于P.
∵四边形ABCD是正方形,
∴AD=AB,∠ABN=∠DAP=90°,
∵AN⊥DP,
∴∠APD+∠PAH=90°,∠ANB+∠PAH=90°,
∴∠APD=∠ANB,
∴△ADP≌△BAN,
∴AN=DP,
∵BF⊥EC,
∴∠EBF+∠BEF=90°,∠BCE+∠BEC=90°,
∴∠EBF=∠BCE,
∴tan∠EBF=tan∠BCE=,
∵AB=BC,BE=AE,
∴tan∠EBF=tan∠BCE=,设EF=a,则BF=2a,CF=4a,
∵PE∥DC,
∴==,
∵CD=4,
∴PE=1,
∵BE=2,
∴PE=PB=1,
∴PF=BE=1,AP=3,
在Rt△ADP中,DP==5,
∴DF=4,BN=AP=3,CN=1,
∴DC=DF,
∴∠DFC=∠DCF,
∵∠BCE+∠DCF=90°,∠FMH+∠DFC=90°,∠FMH=∠NMC,
∴∠NCM=∠NMC,
∴MN=CN=1.
故答案为1.
21.解:(1)如图1,连接AC,
∵四边形ABCD是正方形,
∴∠DAC=45°,
∵点F为等边△DCE边CE的中点,
∴DF是CE的垂直平分线,
∴GE=GC,
∵∠ADE=90°+60°=150°,AD=DE,
∴∠DAE=∠DEA=15°,
∴∠GEC=∠GCE=60°﹣15°=45°,
∴GC⊥AE,
∴△AGC为直角三角形,
∵∠GAC=∠DAC﹣∠DAE=45°﹣15°=30°,AG=2,
∴GC=GE=AG=2;
故答案为:2;
(2)由(1)可得AC=4,则DC=2,
在等边△DCE中DF=,
在等腰直角△CGE中,由斜边上中线等于斜边的一半得GF=,
∴DG=﹣.
(3)如图2,过D作DN⊥AE于N,过A作AM⊥AE交GD的延长线于M,
∵∠ADN+∠CDN=90°,∠ADN+∠DAN=90°,
∴∠DAN=∠CDN,
∵AD=DC=DE,
∴∠DAN=∠CDN=∠DEA,
∵F是CE中点,
∴∠CDF=∠EDF,
∵∠NDG=∠CDN+∠CDF,∠DGN=∠DEA+∠EDF,
∴∠NDG=∠DGN=45°,
∴∠M=45°,
∴AM=AG,
∵∠DAM+∠DAN=90°,∠BAG+∠DAN=90°,
∴∠DAM=∠BAG,
在△MAD和△GAB中,
,
∴△MAD≌△GAB(SAS),
∴BG=DM,
∴BG+DG=DM+DG=MG=AG=×2=2.
22.解:(1)∵四边形ABCD是平行四边形,
∴AD=BC=4,AB∥CD,AB=CD=3,
∵E为BC中点,
∴BE=CE=2,
∵∠B=60°,EF⊥AB,
∴∠FEB=30°,
∴BF=1,
由勾股定理得:EF=;
(2)∵AB∥CD,
∴∠B=∠ECH,
在△BFE和△CHE中,
,
∴△BFE≌△CHE(ASA),
∴EF=EH=,CH=BF=1,
∵S△DHF=DH?FH=4,
∴S△DEF=S△DHF=2.
23.(1)证明:如图①,作∠GAH=∠EAB交GE于点H.
∴∠GAB=∠HAE.
∵∠EAB=∠EGB,∠APE=∠BPG,
∴∠ABG=∠AEH.
在△ABG和△AEH中,
,
∴△ABG≌△AEH(ASA).
∴BG=EH,AG=AH.
∵∠GAH=∠EAB=60°,
∴△AGH是等边三角形.
∴AG=HG.
∴EG=AG+BG;
(2)EG=AG﹣BG.
如图②,作∠GAH=∠EAB交GE于点H.
∴∠GAB=∠HAE.
∵∠EGB=∠EAB=90°,
∴∠ABG+∠AEG=∠AEG+∠AEH=180°.
∴∠ABG=∠AEH.
∵又AB=AE,
∴△ABG≌△AEH.
∴BG=EH,AG=AH.
∵∠GAH=∠EAB=90°,
∴△AGH是等腰直角三角形.
∴AG=HG.
∴EG=AG﹣BG.
24.(1)证明:过C点作CH⊥BF于H点,
∵∠CFB=45°
∴CH=HF,
∵∠ABG+∠BAG=90°,∠FBE+∠ABG=90°
∴∠BAG=∠FBE,
∵AG⊥BF,CH⊥BF,
∴∠AGB=∠BHC=90°,
在△AGB和△BHC中,
∵∠AGB=∠BHC,∠BAG=∠HBC,AB=BC,
∴△AGB≌△BHC,
∴AG=BH,BG=CH,
∵BH=BG+GH,
∴BH=HF+GH=FG,
∴AG=FG;
(2)方法1、解:∵CH⊥GF,
∴CH∥GM,
∵C为FM的中点,
∴CH=GM,
∴BG=GM,
∵BM=10,
∴BG=2,GM=4,
∴AG=4,AB=10,
∴HF=2,
∴CF=2×=2,
∴CM=2,
过B点作BK⊥CM于K,
∵CK=CM=CF=,
∴BK=3,
过D作DQ⊥MF交MF延长线于Q,
∴△BKC≌△CQD
∴CQ=BK=3,
DQ=CK=,
∴QF=3﹣2=,
∴DF==2.
25.解:(1)∵正方形ABCD中,∠A=∠BCD=90°,则
∠DCF=∠A=90°,AD=CD,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(SAS);
(2)∵AB=BC=3,CF=AE=1,
∴BE=3﹣1=2,BF=3+1=4,
∴Rt△BEF中,EF===2.
26.(1)解:如图2中,
∵四边形ABCD是菱形,
∴AD=AB,
∵∠A=60°,
∴△ABD是等边三角形,
∴AB=DB,∠A=∠FDB=60°,
在△DAE和△BDF中,
,
∴△DAE≌△BDF,
∴∠ADE=∠DBF,
∵∠EGB=∠GDB+∠GBD=∠GDB+∠ADE=60°,
∴∠BGD=180°﹣∠BGE=120°.
(2)证明:如图3中,延长GE到M,使得GM=GB,连接BD、CG.
∵∠MGB=60°,GM=GB,
∴△GMB是等边三角形,
∴∠MBG=∠DBC=60°,
∴∠MBD=∠GBC,
在△MBD和△GBC中,
,
∴△MBD≌△GBC,
∴DM=GC,∠M=∠CGB=60°,
∵CH⊥BG,
∴∠GCH=30°,
∴CG=2GH,
∵CG=DM=DG+GM=DG+GB,
∴2GH=DG+GB.
27.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠ABC+∠BAD=180°.
又∵AB=AC,
∴∠ABC=∠ACB.
∵∠ACB+∠ACE=180°,
∴∠BAD=∠ACE.
∵CE=BC,
∴CE=AD,
在△ABE和△CEA中,,
∴△ADB≌△CEA(SAS).
(2)解:∵△ADB≌△CEA,
∴AE=BD=9.
∵AD∥BC,
∴△ADF∽△EBF.
∴=.
∴=.
∴AF=3.
28.(1)①证明:∵四边形ABCD是正方形,
∴AD∥BC,
∵AP∥DQ,
∴四边形APQD为平行四边形;
②解:结论:OA=OP,OA⊥OP,理由如下:
∵四边形ABCD是正方形,
∴AB=BC=PQ,∠ABO=∠OBQ=45°,
∵OQ⊥BD,
∴∠PQO=45°,
∴∠ABO=∠OBQ=∠PQO=45°,
∴OB=OQ,
在△AOB和△OPQ中,
,
∴△AOB≌△POQ(SAS),
∴OA=OP,∠AOB=∠POQ,
∴∠AOP=∠BOQ=90°,
∴OA⊥OP;
(2)如图,过O作OE⊥BC于E.
①如图1,当P点在B点右侧时,
则BQ=1+2=3,OE=BQ=,
∴S△OPB=×1×=
②如图2,当P点在B点左侧时,
则BQ=2﹣1=1,OE=BQ=,
∴S△PBO=×1×=,
综上所述,△POB的面积为或.
1.如图,四边形ABCD是平行四边形,下列说法不正确的是( )
A.当AC=BD时,四边形ABCD是矩形
B.当AB=BC时,四边形ABCD是菱形
C.当AC平分∠BAD时,四边形ABCD是菱形
D.当∠DAB=90°时,四边形ABCD是正方形
2.如图,矩形ABCD中,BC>AB,对角线AC、BD交于O点,且AC=10,过B点作BE⊥AC于E点,若BE=4,则AD的长等于( )
A.8 B.10 C.3 D.4
3.如图,在平行四边形ABCD中,AD=6,点E在边AD上,点F在BC的延长线上,且满足BF=BE=8,过点C作CE的垂线交BE于点G,若CE恰好平分∠BEF,则BG的长为( )
A.2 B.3 C.4 D.2
4.如图,在正方形ABCD中,M为边BC上的一点,MN⊥BC交BD于点N,连接AM交BD于点E,F为DN中点,连接AF.有下列说法:①BN=BM;②∠BAF=∠AEF;③BE2+DF2=EF2;④AB﹣MN=DF.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
5.如图,正方形ABCO和正方形DEFO的顶点A,E,O在同一直线l上,且EF=2,AB=6,给出下列结论:①AE=10,②∠COD=45°,③△COF的面积S△COF=6,
④CF=BD=2,其中正确的是( )
A.①②③ B.②③④ C.①②④ D.①③④
6.如图,在矩形ABCD中,DE⊥AC于E,∠EDC:∠EDA=1:3,且AC=10,则OE的长度是( )
A. B.5 C.3 D.
7.如图,在矩形ABCD中,AB=2,AD=1,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值是( )
A.2 B.4 C. D.2
8.如图,正方形ABCD的边长AB=8,E为平面内一动点,且AE=4,F为CD上一点,CF=2,连接EF,ED,则EF+ED的最小值为( )
A.6 B.4 C.4 D.6
9.如图,AB⊥AF,EF⊥AF,BE与AF交于点C,点D是BC的中点,∠AEB=2∠B.若BC=8,EF=,则AF的长是( )
A. B. C.3 D.5
10.如图,在矩形OABC中,点B的坐标是(1,3),则AC的长是( )
A.3 B.2 C. D.4
11.矩形ABCD的周长是34cm,对角线相交于O,△AOD与△AOB的周长相差1cm,则AB的长是 .
12.已知:如图,∠MON=90°,四边形ABCD为矩形,A、B两点分别在射线ON、OM上,AD=2,AB=4,A、B两点在ON、OM上滑动时,C、D点随之运动,则线段OD的最大值为 .
13.如图,?ABCD中,AB=10cm,AD=15cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,点P到达点D时停止(同时点Q也停止运动),在运动以后,当以点P、D、Q、B为顶点组成平行四边形时,运动时间t为 秒.
14.如图,在正方形ABCD中,动点E、F分别从D、C两点同时出发,以相同的速度在直线DC、CB上移动,连接AE和DF交于P,若AD=6,则线段CP的最小值为 .
15.如图,在四边形ABCD中,AB⊥BC,对角线AC、BD相交于点E,E为BD中点,且AD=BD,AB=2,∠BAC=30°,则DC= .
16.如图,四边形ABCD为正方形,AB为边向正方形外作等边三角形ABE、CE与DB相交于点F,则∠AFD= 度.
17.如图,点M为正方形ABCD边CD的中点,连接AM、BM,BM交对角线AC于点P,连接PD交AM于点Q,如果AB长为9,那么PQ的长为 .
18.如图,M为矩形ABCD中AD边中点,E、F分别为BC、CD上的动点,且BE=2DF,若AB=1,BC=2,则ME+2AF的最小值为 .
19.已知:正方形ABCD中,对角线AC、BD相交于点O,∠DBC的平分线BF交CD于点E,交AC于点F,OF=1,则AB= .
20.已知如图,正方形ABCD的边长为4,取AB边上的中点E,连接CE,过点B作BF⊥CE于点F,连接DF.过点A作AH⊥DF于点H,交CE于点M,交BC于点N,则MN= .
21.如图,已知正方形ABCD和等边△DCE,点F为CE的中点,AE与DF相交于点G,AG=2.
(1)直接写出GE= ;
(2)求出DG的长;
(3)如图,若将题中“等边△DCE”改为“DC=DE的等腰△DCE”,其他条件不变,求出BG+DG的值.
22.如图,在?ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H.
(1)求EF的长;
(2)求△DEF的面积.
23.在平行四边形ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
(1)如图①,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图②,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.
24.如图1,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°
(1)求证:AG=FG;
(2)如图2延长FC、AE交于点M,连接DF、BM,若C为FM中点,BM=10,求FD的长.
25.如图,四边形ABCD是正方形,E、F分别是AB和BC延长线上的点,且AE=CF.
(1)求证:△ADE≌△CDF;
(2)连接EF,若AB=3,AE=1,求EF的长.
26.如图1,菱形ABCD中,∠BAD=60°,点E、F分别是边AB、AD上两个动点,满足AE=DF,连接BF与DE相交于点G.
(1)如图2,连接BD,求∠BGD的度数;
(2)如图3,作CH⊥BG于H点,求证:2GH=DG+BG.
27.如图,平行四边形ABCD中,AC与BD相交于点O,AB=AC,延长BC到点E,使CE=BC,连接AE,分别交BD、CD于点F、G.
(1)求证:△ADB≌△CEA;
(2)若BD=9,求AF的长.
28.已知四边形ABCD是正方形,点P,Q在直线BC上,且AP∥DQ,过点Q作QO⊥BD,垂足为点O,连接OA,OP.
(1)如图,点P在线段BC上,
①求证:四边形APQD是平行四边形;
②判断OA,OP之间的数量关系和位置关系,并加以证明;
(2)若正方形ABCD的边长为2,直接写出BP=1时,△OBP的面积.
参考答案
1.解:①由矩形的判定“对角线相等的平行四边形是矩形”可知,A正确;
②由菱形的判定“有一组邻边相等的平行四边形是菱形”可知,B正确;
③∵AC平分∠BAD,
∴∠DAC=∠CAB,
∵CD∥AB,
∴∠DCA=∠CAB,
∴∠DAC=∠DCA,
∴DA=DC,
∴平行四边形ABCD是菱形,故C正确;
④在平行四边形ABCD中,
∵∠DAB=90°,
∴平行四边形ABCD是矩形,而不能判定其是正方形,故D错误;
故选:D.
2.解:∵四边形ABCD是矩形,
∴∠BAD=90°,设AD=BC=a,AB=DC=b,
∵AC=10,BE⊥AC,BE=4,
∴a2+b2=102,
又∵S矩形ABCD=2S△ABC
∴ab=2××10×4=40,
∵BC>AB,
解得:a=4,b=2,
即AD=4,
故选:D.
3.解:如图,延长EF,GC两条线相交于点H,过点G作GP∥EF交BC于点P,
∵四边形ABCD是平行四边形,
∴BC=AD=6,
∵BF=BE=8,
∴CF=BF﹣BC=2,
∵CE平分∠BEF,
∴∠GEC=∠HEC,
∵CE⊥GC,
∴∠ECG=∠ECH=90°,
在△ECG和△ECH中,
,
∴△ECG≌△ECH(ASA),
∴CG=CH,
∵GP∥EF,
∴∠PGC=∠FHC,
在△PCG和△FCH中,
,
∴△PCG≌△FCH(ASA),
∴CP=CF=2,
∴BP=BF﹣PF=8﹣4=4,
∵BF=BE,
∴∠BEF=∠BFE,
∵GP∥EF,
∴∠BGP=∠BEF,∠BPG=∠BFE,
∴∠BGP=∠BPG,
∴BG=BP=4.
故选:C.
4.解:①∵四边形ABCD是正方形,
∴∠DBC=45°,
∵MN⊥BC,
∴∠BMN=90°,
∴△MNB是等腰直角三角形,
∴BM=MN,
∴BN=BM;
故①正确;
②过F作GH⊥BC于H,交AD于G,连接FM、FC,
∵AD∥BC,
∴GH⊥AD,
∵四边形ABCD是正方形,
∴AD=BC,∠ADF=∠CDF=45°,
∵DF=DF,
∴△ADF≌△CDF,
∴AF=CF,
∵∠FDG=45°,∠FGD=90°,
∴△FGD是等腰直角三角形,
∴FG=DG=CH,
∴Rt△AFG≌Rt△FCH(HL),
∴∠FAG=∠CFH,
∵MN∥FH∥DC,F是DN的中点,
∴MH=CH,
∵FH⊥CM,
∴FM=FC,
∴∠MFH=∠CFH=∠FAG,
∵∠AGF=∠FAG+∠AFG=∠MFH+∠AFG=90°,
∴∠AFM=90°,
∵AF=FC=FM,
∴△AFM是等腰直角三角形,
∴∠MAF=45°,
∵∠BAF=∠BAM+∠MAF=∠BAM+45°,
∠AEF=∠BAM+∠ABE=∠BAM+45°,
∴∠BAF=∠AEF;
故②正确;
③∵AD=AB,∠DAB=90°,
∴将△AFD绕点A顺时针旋转90°至△ABF',
∴△AFD≌△AF'B,
∴DF=BF',∠ABF'=∠ADF=45°,AF=AF',
∴∠EBF'=45°+45°=90°,
∴EF'2=BF'2+BE2=DF2+BE2,
∵∠F'AE=∠F'AB+∠BAE=∠FAD+∠BAE=45°=∠EAF,AN=AN,
∴△F'AE≌△FAE,
∴EF=EF',
∴EF2=BE2+DF2;
故③正确;
④过F作FR⊥CD,垂足为P,使FP=PR,连接DR、RC,
∵∠FDP=45°,
∴∠DFP=45°,
∴FP=PD=PR,
∴∠FDR=90°,△FDR是等腰直角三角形,
∴FR=DF,
∵FR=2FP,CM=2CH=2FP,
∴FR=CM,
∵AB=CB,BM=MN,
∴CM=BC﹣BM=AB﹣BM=AB﹣MN,
∴AB﹣MN=DF,
故④正确;
本题正确的结论有:①②③④,4个故选:D.
5.解:①∵EF=2,
∴OE=4,
∵AO=AB=6,
∴AE=AO+OE=6+4=10,故正确;
②∵∠AOC=90°,∠DOE=45°,
∴∠COD=180°﹣∠AOC﹣∠DOE=45°,故正确;
③作FG⊥CO交CO的延长线于G,
则FG=2,
∴△COF的面积S△COF=×6×2=6,故正确;
④作DH⊥AB于H,
CF==2,
BH=6﹣2=4,
DH=6+2=8,
BD==4,故错误.故选:A.
6.解:∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD=10,OA=OC=AC=5,OB=OD=BD=5,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠EDC:∠EDA=1:3,∠EDC+∠EDA=90°,
∴∠EDC=22.5°,∠EDA=67.5°,
∵DE⊥AC,
∴∠DEC=90°,
∴∠DCE=90°﹣∠EDC=67.5°,
∴∠ODC=∠OCD=67.5°,
∴∠ODC+∠OCD+∠DOC=180°,
∴∠COD=45°,
∴OE=DE,
∵OE2+DE2=OD2,
∴(2DE)2=OD2=25,
∴DE=,故选:D.
7.解:如图:
当点F与点C重合时,点P在P1处,CP1=DP1,
当点F与点E重合时,点P在P2处,EP2=DP2,
∴P1P2∥CE且P1P2=CE.
当点F在EC上除点C、E的位置处时,有DP=FP.
由中位线定理可知:P1P∥CE且P1P=CF.
∴点P的运动轨迹是线段P1P2,
∴当BP⊥P1P2时,PB取得最小值.
∵矩形ABCD中,AB=2,AD=1,E为AB的中点,
∴△CBE、△ADE、△BCP1为等腰直角三角形,CP1=1.
∴∠ADE=∠CDE=∠CP1B=45°,∠DEC=90°.
∴∠DP2P1=90°.
∴∠DP1P2=45°.
∴∠P2P1B=90°,即BP1⊥P1P2,
∴BP的最小值为BP1的长.
在等腰直角BCP1中,CP1=BC=1.
∴BP1=.
∴PB的最小值是.故选:C.
8.解:如图,当点E运动到点E′时,EF+ED的值最小,最小值为EF+DE',
在AD边上取AH=2,
∵AE′=AE=4,
∴=2,
∵AD=8,
∴=2,
∴,
∵∠DAE′=∠E′AH,
∴△DAE′∽△E′AH,
∴=2,
∴E′H=DE',
∴EF+ED=EF+E′D=EF+E′H=HF,
∴EF+ED的最小值为HF的值,
∵DH=AD﹣AH=6,
DF=DC﹣CF=6,
在Rt△DHF中,根据勾股定理,得
HF=,故选:A.
9.解:∵AB⊥AF,
∴∠FAB=90°,
∵点D是BC的中点,
∴AD=BD=BC,
∴∠DAB=∠B,
∴∠ADE=∠B+∠BAD=2∠B,
∵∠AEB=2∠B,
∴∠AED=∠ADE,
∴AE=AD,
∵BC=8,
∴AE=AD=4,
∵EF=,EF⊥AF,
∴AF===3,
故选:C.
10.解:
连接OB,过B作BM⊥x轴于M,
∵点B的坐标是(1,3),
∴OM=1,BM=3,由勾股定理得:OB==,
∵四边形OABC是矩形,
∴AC=OB,
∴AC=,
故选:C.
11.解:由图易得:OB=OD,那么△AOD与△AOB的周长相差1cm其实就是AD与AB相差1cm
当AD比AB长1cm时,AD+AB=AB+1+AB=17,AB=8;
当AD比AB短1cm时,AD+AB=AB﹣1+AB=17,AB=9.
因此AB的长为8或9cm.故AB的长为8或9cm.
12.解:如图,取AB的中点E,连接OE、DE、OD,
∵OD<OE+DE,
∴当O、D、E三点共线时,点D到点O的距离最大,
此时,∵AB=4,BC=2,
∴OE=AE=AB=2,
DE==2,
∴OD的最大值为:2+2.
故答案为:2+2.
13.解:设经过t秒,以点P、D、Q、B为顶点组成平行四边形,
∵P在AD上运动,
∴t≤,即t≤15,
∵以点P、D、Q、B为顶点组成平行四边形,
∴DP=BQ,
分为以下情况:①点Q的运动路线是C﹣B﹣C,方程为4t﹣15=15﹣t,
解得:t=6;
②点Q的运动路线是C﹣B﹣C﹣B,方程为15﹣(4t﹣30)=15﹣t,
解得:t=10;
③点Q的运动路线是C﹣B﹣C﹣B﹣C,方程为4t﹣45=15﹣t,
解得:t=12;
故答案为:6或10或12.
14.解:由题意得:AD=CD,DE=FC,∠ADC=∠DCF=90°,
∴△DCF≌△ADE(SAS),∴∠DAE=∠FDC,
∴∠APD=90°,即:相当于点P始终在以AD为直径的圆上,
取AD的中点Q,当Q、P、C三点共线时,PC最小,
PC=CQ﹣PQ=﹣3=3﹣3.
故:答案是3﹣3.
15.解:如图,在EA上取一点K,使得EK=CE,连接DK,BK,延长DK交AB于H.
∵DE=EB,CE=EK,
∴四边形BCDK是平行四边形,
∴CD=BK,DK∥BC,
∵BC⊥AB,
∴DH⊥AB,
∵DA=DB,
∴AH=HB=1,
∴KA=KB=CD,
在Rt△AKH中,AK=AH÷cos30°=,
∴CD=,
故答案为.
16.解:∵∠CBA=90°,∠ABE=60°,
∴∠CBE=150°,
∵四边形ABCD为正方形,三角形ABE为等边三角形
∴BC=BE,
∴∠BEC=15°,
∵∠FBE=∠DBA+∠ABE=105°,
∴∠BFE=60°,
在△CBF和△ABF中,
,
∴△CBF≌△ABF(SAS),
∴∠BAF=∠BCE=15°,
又∠ABF=45°,且∠AFD为△AFB的外角,
∴∠AFD=∠ABF+∠FAB=15°+45°=60°.
故答案为60.
17.解:如图,延长P交BC于H.
∵四边形ABCD是正方形,
∴AB=CD=AD=BC=9,AB∥CD,AD∥BC,
∵DM=CM=4.5,
∴PC:PA=CM:AB=1:2,CH:AD=CP:PA=1:2,
∴AD=2CH,
∴CB=2CH,
∴CH=BH=4.5,
∵AD=CD,∠ADM=∠DCH,DM=CH,
∴△ADM≌△DCH,
∴∠DAM=∠CDH,
∵∠DAM+∠AMD=90°,
∴∠CDH+∠DMA=90°,
∴∠DQM=90°,
∵DH==,
∵DP{PH=AD:CH=2:1,
∴DP=DH=3,
∵AM=DH=,
∴DQ==,
∴PQ=PD﹣DQ=,
故答案为.
18.解:如图,过点M作MH⊥BC于H.设DF=x,则BE=2x.
∵四边形ABCD是矩形,
∴∠BAD=∠B=∠D=90°,
∵MH⊥BC,
∴∠MHB=90°,
∴四边形ABHM是矩形,
∴AM=DM=BH=1,AB=MH=1,
∴EH=1﹣2x,
∴ME+2AF=+2=+,
欲求ME+2AF的最小值,相当于在x轴上找一点Q(2x,0),使得点Q到J(0,4),和K(1,1)的距离之和最小(如下图),
作点J关于x轴的对称点J′,连接KJ′交x轴于Q,连接JQ,此时JQ+QK的值最小,最小值=KJ′,
∵J′(0,﹣4),K(1,1),
∴KJ′==,
∴ME+2AF的最小值为,
故答案为.
19.解:如图作FH∥BC交BD于点H.
∵四边形ABCD是正方形,
∴∠OBC=∠OCB=45°,OB=OC,∠BOC=90°
∵FH∥BC,
∴∠OHF=∠OBC,∠OFH=∠OCB,
∴∠OHF=∠OFH,
∴OH=OF=1,FH==,
∵BF平分∠OBC,
∴∠HBF=∠FBC=∠BFH,
∴BH=FH=,
∴OB=OC=1+,
∴BC=OB=2+.
故答案为2+.
20.解:如图,延长DF交AB于P.
∵四边形ABCD是正方形,
∴AD=AB,∠ABN=∠DAP=90°,
∵AN⊥DP,
∴∠APD+∠PAH=90°,∠ANB+∠PAH=90°,
∴∠APD=∠ANB,
∴△ADP≌△BAN,
∴AN=DP,
∵BF⊥EC,
∴∠EBF+∠BEF=90°,∠BCE+∠BEC=90°,
∴∠EBF=∠BCE,
∴tan∠EBF=tan∠BCE=,
∵AB=BC,BE=AE,
∴tan∠EBF=tan∠BCE=,设EF=a,则BF=2a,CF=4a,
∵PE∥DC,
∴==,
∵CD=4,
∴PE=1,
∵BE=2,
∴PE=PB=1,
∴PF=BE=1,AP=3,
在Rt△ADP中,DP==5,
∴DF=4,BN=AP=3,CN=1,
∴DC=DF,
∴∠DFC=∠DCF,
∵∠BCE+∠DCF=90°,∠FMH+∠DFC=90°,∠FMH=∠NMC,
∴∠NCM=∠NMC,
∴MN=CN=1.
故答案为1.
21.解:(1)如图1,连接AC,
∵四边形ABCD是正方形,
∴∠DAC=45°,
∵点F为等边△DCE边CE的中点,
∴DF是CE的垂直平分线,
∴GE=GC,
∵∠ADE=90°+60°=150°,AD=DE,
∴∠DAE=∠DEA=15°,
∴∠GEC=∠GCE=60°﹣15°=45°,
∴GC⊥AE,
∴△AGC为直角三角形,
∵∠GAC=∠DAC﹣∠DAE=45°﹣15°=30°,AG=2,
∴GC=GE=AG=2;
故答案为:2;
(2)由(1)可得AC=4,则DC=2,
在等边△DCE中DF=,
在等腰直角△CGE中,由斜边上中线等于斜边的一半得GF=,
∴DG=﹣.
(3)如图2,过D作DN⊥AE于N,过A作AM⊥AE交GD的延长线于M,
∵∠ADN+∠CDN=90°,∠ADN+∠DAN=90°,
∴∠DAN=∠CDN,
∵AD=DC=DE,
∴∠DAN=∠CDN=∠DEA,
∵F是CE中点,
∴∠CDF=∠EDF,
∵∠NDG=∠CDN+∠CDF,∠DGN=∠DEA+∠EDF,
∴∠NDG=∠DGN=45°,
∴∠M=45°,
∴AM=AG,
∵∠DAM+∠DAN=90°,∠BAG+∠DAN=90°,
∴∠DAM=∠BAG,
在△MAD和△GAB中,
,
∴△MAD≌△GAB(SAS),
∴BG=DM,
∴BG+DG=DM+DG=MG=AG=×2=2.
22.解:(1)∵四边形ABCD是平行四边形,
∴AD=BC=4,AB∥CD,AB=CD=3,
∵E为BC中点,
∴BE=CE=2,
∵∠B=60°,EF⊥AB,
∴∠FEB=30°,
∴BF=1,
由勾股定理得:EF=;
(2)∵AB∥CD,
∴∠B=∠ECH,
在△BFE和△CHE中,
,
∴△BFE≌△CHE(ASA),
∴EF=EH=,CH=BF=1,
∵S△DHF=DH?FH=4,
∴S△DEF=S△DHF=2.
23.(1)证明:如图①,作∠GAH=∠EAB交GE于点H.
∴∠GAB=∠HAE.
∵∠EAB=∠EGB,∠APE=∠BPG,
∴∠ABG=∠AEH.
在△ABG和△AEH中,
,
∴△ABG≌△AEH(ASA).
∴BG=EH,AG=AH.
∵∠GAH=∠EAB=60°,
∴△AGH是等边三角形.
∴AG=HG.
∴EG=AG+BG;
(2)EG=AG﹣BG.
如图②,作∠GAH=∠EAB交GE于点H.
∴∠GAB=∠HAE.
∵∠EGB=∠EAB=90°,
∴∠ABG+∠AEG=∠AEG+∠AEH=180°.
∴∠ABG=∠AEH.
∵又AB=AE,
∴△ABG≌△AEH.
∴BG=EH,AG=AH.
∵∠GAH=∠EAB=90°,
∴△AGH是等腰直角三角形.
∴AG=HG.
∴EG=AG﹣BG.
24.(1)证明:过C点作CH⊥BF于H点,
∵∠CFB=45°
∴CH=HF,
∵∠ABG+∠BAG=90°,∠FBE+∠ABG=90°
∴∠BAG=∠FBE,
∵AG⊥BF,CH⊥BF,
∴∠AGB=∠BHC=90°,
在△AGB和△BHC中,
∵∠AGB=∠BHC,∠BAG=∠HBC,AB=BC,
∴△AGB≌△BHC,
∴AG=BH,BG=CH,
∵BH=BG+GH,
∴BH=HF+GH=FG,
∴AG=FG;
(2)方法1、解:∵CH⊥GF,
∴CH∥GM,
∵C为FM的中点,
∴CH=GM,
∴BG=GM,
∵BM=10,
∴BG=2,GM=4,
∴AG=4,AB=10,
∴HF=2,
∴CF=2×=2,
∴CM=2,
过B点作BK⊥CM于K,
∵CK=CM=CF=,
∴BK=3,
过D作DQ⊥MF交MF延长线于Q,
∴△BKC≌△CQD
∴CQ=BK=3,
DQ=CK=,
∴QF=3﹣2=,
∴DF==2.
25.解:(1)∵正方形ABCD中,∠A=∠BCD=90°,则
∠DCF=∠A=90°,AD=CD,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(SAS);
(2)∵AB=BC=3,CF=AE=1,
∴BE=3﹣1=2,BF=3+1=4,
∴Rt△BEF中,EF===2.
26.(1)解:如图2中,
∵四边形ABCD是菱形,
∴AD=AB,
∵∠A=60°,
∴△ABD是等边三角形,
∴AB=DB,∠A=∠FDB=60°,
在△DAE和△BDF中,
,
∴△DAE≌△BDF,
∴∠ADE=∠DBF,
∵∠EGB=∠GDB+∠GBD=∠GDB+∠ADE=60°,
∴∠BGD=180°﹣∠BGE=120°.
(2)证明:如图3中,延长GE到M,使得GM=GB,连接BD、CG.
∵∠MGB=60°,GM=GB,
∴△GMB是等边三角形,
∴∠MBG=∠DBC=60°,
∴∠MBD=∠GBC,
在△MBD和△GBC中,
,
∴△MBD≌△GBC,
∴DM=GC,∠M=∠CGB=60°,
∵CH⊥BG,
∴∠GCH=30°,
∴CG=2GH,
∵CG=DM=DG+GM=DG+GB,
∴2GH=DG+GB.
27.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠ABC+∠BAD=180°.
又∵AB=AC,
∴∠ABC=∠ACB.
∵∠ACB+∠ACE=180°,
∴∠BAD=∠ACE.
∵CE=BC,
∴CE=AD,
在△ABE和△CEA中,,
∴△ADB≌△CEA(SAS).
(2)解:∵△ADB≌△CEA,
∴AE=BD=9.
∵AD∥BC,
∴△ADF∽△EBF.
∴=.
∴=.
∴AF=3.
28.(1)①证明:∵四边形ABCD是正方形,
∴AD∥BC,
∵AP∥DQ,
∴四边形APQD为平行四边形;
②解:结论:OA=OP,OA⊥OP,理由如下:
∵四边形ABCD是正方形,
∴AB=BC=PQ,∠ABO=∠OBQ=45°,
∵OQ⊥BD,
∴∠PQO=45°,
∴∠ABO=∠OBQ=∠PQO=45°,
∴OB=OQ,
在△AOB和△OPQ中,
,
∴△AOB≌△POQ(SAS),
∴OA=OP,∠AOB=∠POQ,
∴∠AOP=∠BOQ=90°,
∴OA⊥OP;
(2)如图,过O作OE⊥BC于E.
①如图1,当P点在B点右侧时,
则BQ=1+2=3,OE=BQ=,
∴S△OPB=×1×=
②如图2,当P点在B点左侧时,
则BQ=2﹣1=1,OE=BQ=,
∴S△PBO=×1×=,
综上所述,△POB的面积为或.
