2020-2021学年八年级数学北师大版下册 第三章 图形的平移与旋转 单元练习题(word版,含答案)
文档属性
| 名称 | 2020-2021学年八年级数学北师大版下册 第三章 图形的平移与旋转 单元练习题(word版,含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 204.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 00:00:00 | ||
图片预览

文档简介
第三章 图形的平移与旋转 单元测试
一.选择题
1.下列各组图形可以通过平移互相得到的是( )
A. B.
C. D.
2.在平面直角坐标系中,将点P(﹣1,0)向右平移2个单位,再向上平移2个单位,得到点P′,则点P′在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.如图,已知一个斜边长为2的直角三角板的直角顶点与原点重合,两直角边分别落在两个坐标轴上.现将该三角板向右平移使点A与点O重合,得到△OCB′,则点B的对应点B′的坐标是( )
A.(1,0) B.(,) C.(1,) D.(﹣1,)
4.在手工制作课上,张华和李丽用铁丝制作楼梯模型,如图所示,则她们用的铁丝周长( )
A.张华的长 B.李丽的长 C.一样长 D.不能确定
5.下列图形中,是中心对称图形的是( )
A. B. C. D.
6.已知点P(m2+1,﹣1)与点Q关于原点对称,则点Q一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
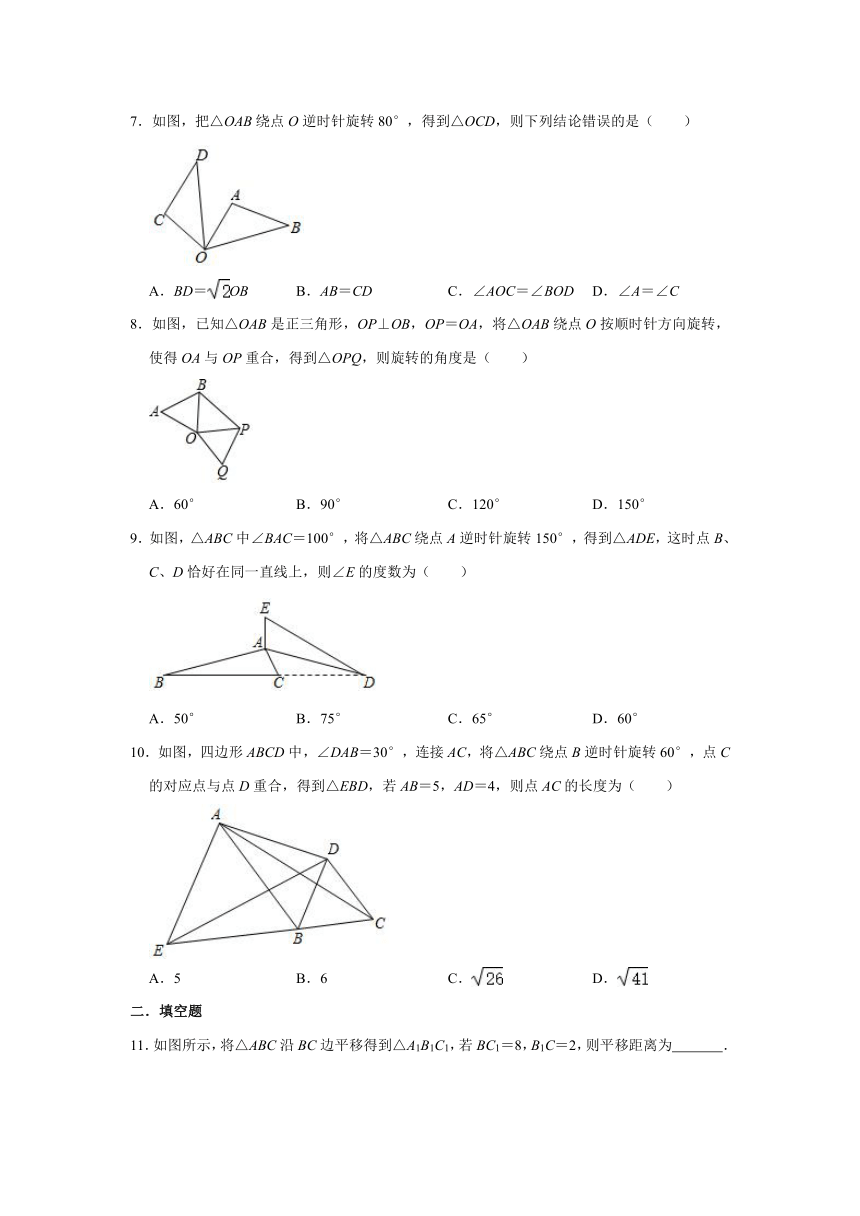
7.如图,把△OAB绕点O逆时针旋转80°,得到△OCD,则下列结论错误的是( )
A.BD=OB B.AB=CD C.∠AOC=∠BOD D.∠A=∠C
8.如图,已知△OAB是正三角形,OP⊥OB,OP=OA,将△OAB绕点O按顺时针方向旋转,使得OA与OP重合,得到△OPQ,则旋转的角度是( )
A.60° B.90° C.120° D.150°
9.如图,△ABC中∠BAC=100°,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B、C、D恰好在同一直线上,则∠E的度数为( )
A.50° B.75° C.65° D.60°
10.如图,四边形ABCD中,∠DAB=30°,连接AC,将△ABC绕点B逆时针旋转60°,点C的对应点与点D重合,得到△EBD,若AB=5,AD=4,则点AC的长度为( )
A.5 B.6 C. D.
二.填空题
11.如图所示,将△ABC沿BC边平移得到△A1B1C1,若BC1=8,B1C=2,则平移距离为 .
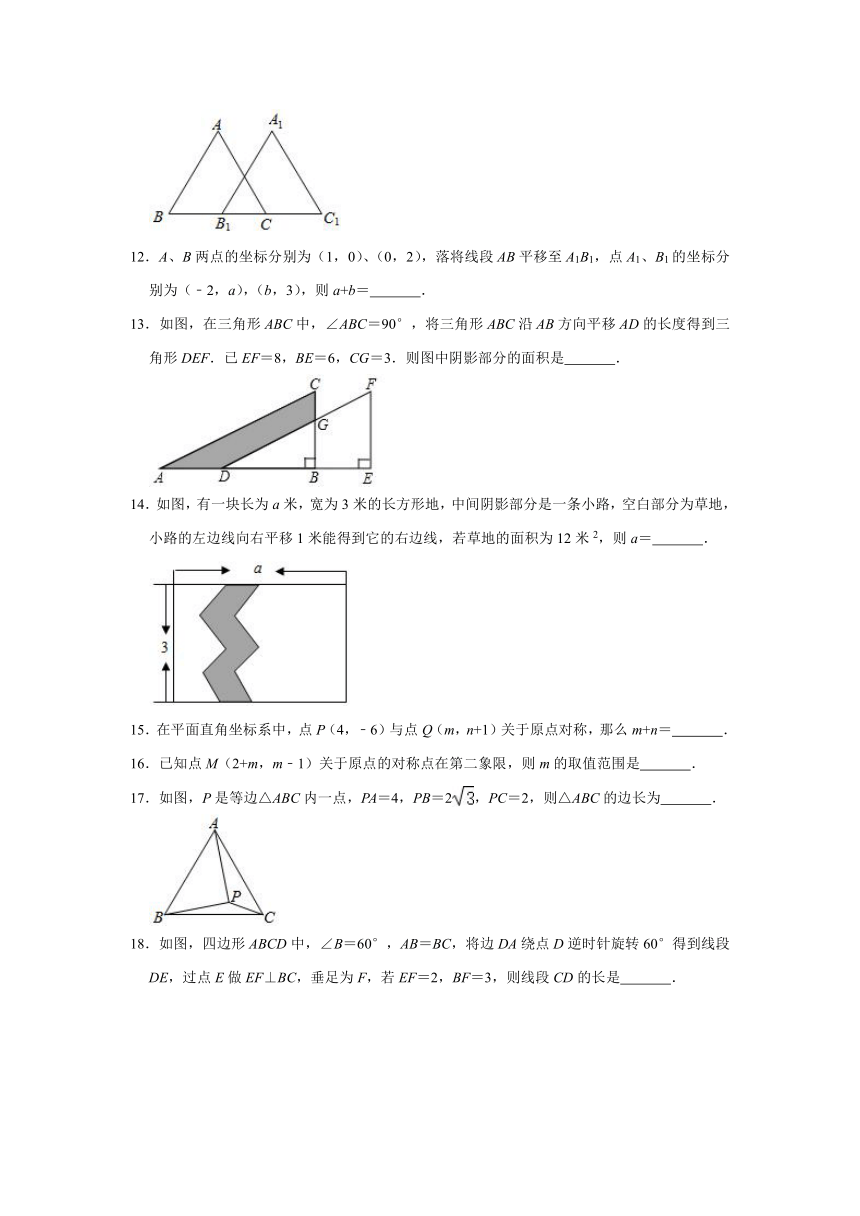
12.A、B两点的坐标分别为(1,0)、(0,2),落将线段AB平移至A1B1,点A1、B1的坐标分别为(﹣2,a),(b,3),则a+b= .
13.如图,在三角形ABC中,∠ABC=90°,将三角形ABC沿AB方向平移AD的长度得到三角形DEF.已EF=8,BE=6,CG=3.则图中阴影部分的面积是 .
14.如图,有一块长为a米,宽为3米的长方形地,中间阴影部分是一条小路,空白部分为草地,小路的左边线向右平移1米能得到它的右边线,若草地的面积为12米2,则a= .
15.在平面直角坐标系中,点P(4,﹣6)与点Q(m,n+1)关于原点对称,那么m+n= .
16.已知点M(2+m,m﹣1)关于原点的对称点在第二象限,则m的取值范围是 .
17.如图,P是等边△ABC内一点,PA=4,PB=2,PC=2,则△ABC的边长为 .
18.如图,四边形ABCD中,∠B=60°,AB=BC,将边DA绕点D逆时针旋转60°得到线段DE,过点E做EF⊥BC,垂足为F,若EF=2,BF=3,则线段CD的长是 .
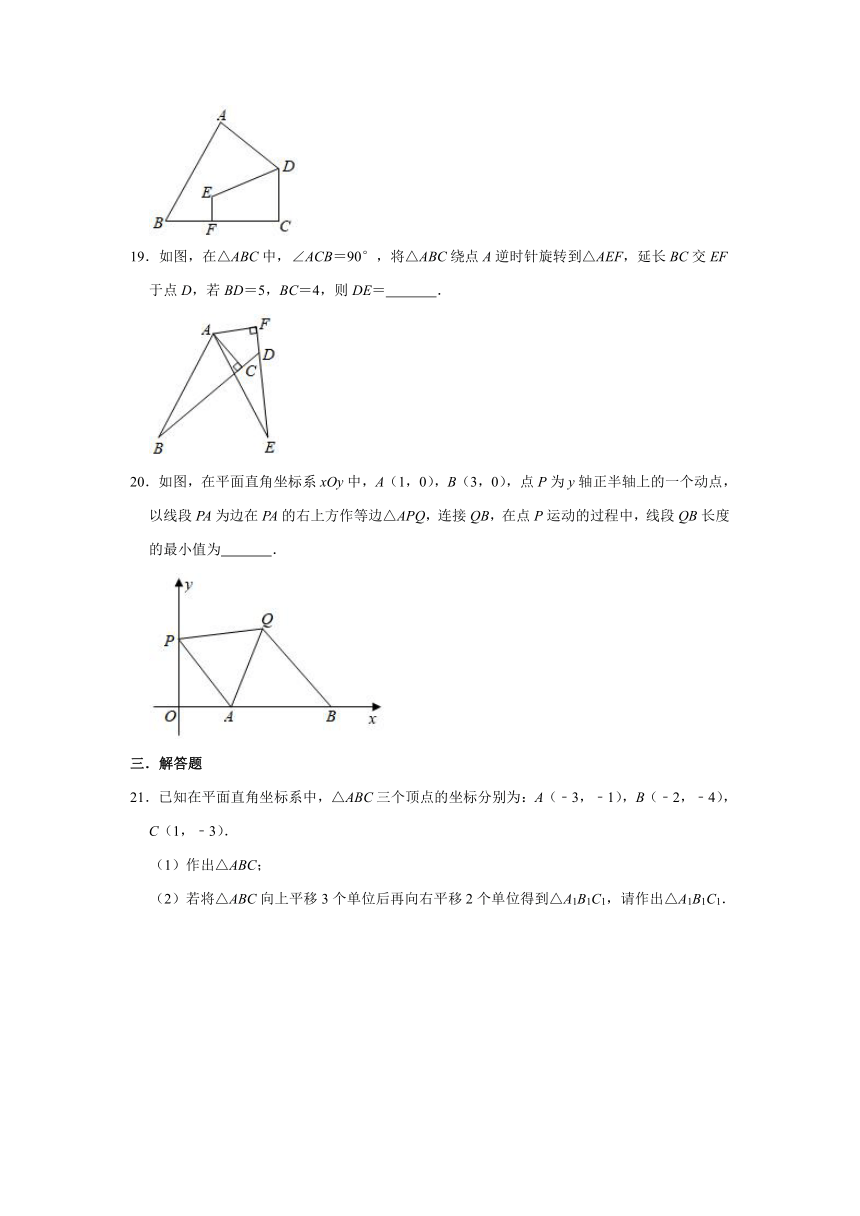
19.如图,在△ABC中,∠ACB=90°,将△ABC绕点A逆时针旋转到△AEF,延长BC交EF于点D,若BD=5,BC=4,则DE= .
20.如图,在平面直角坐标系xOy中,A(1,0),B(3,0),点P为y轴正半轴上的一个动点,以线段PA为边在PA的右上方作等边△APQ,连接QB,在点P运动的过程中,线段QB长度的最小值为 .
三.解答题
21.已知在平面直角坐标系中,△ABC三个顶点的坐标分别为:A(﹣3,﹣1),B(﹣2,﹣4),C(1,﹣3).
(1)作出△ABC;
(2)若将△ABC向上平移3个单位后再向右平移2个单位得到△A1B1C1,请作出△A1B1C1.
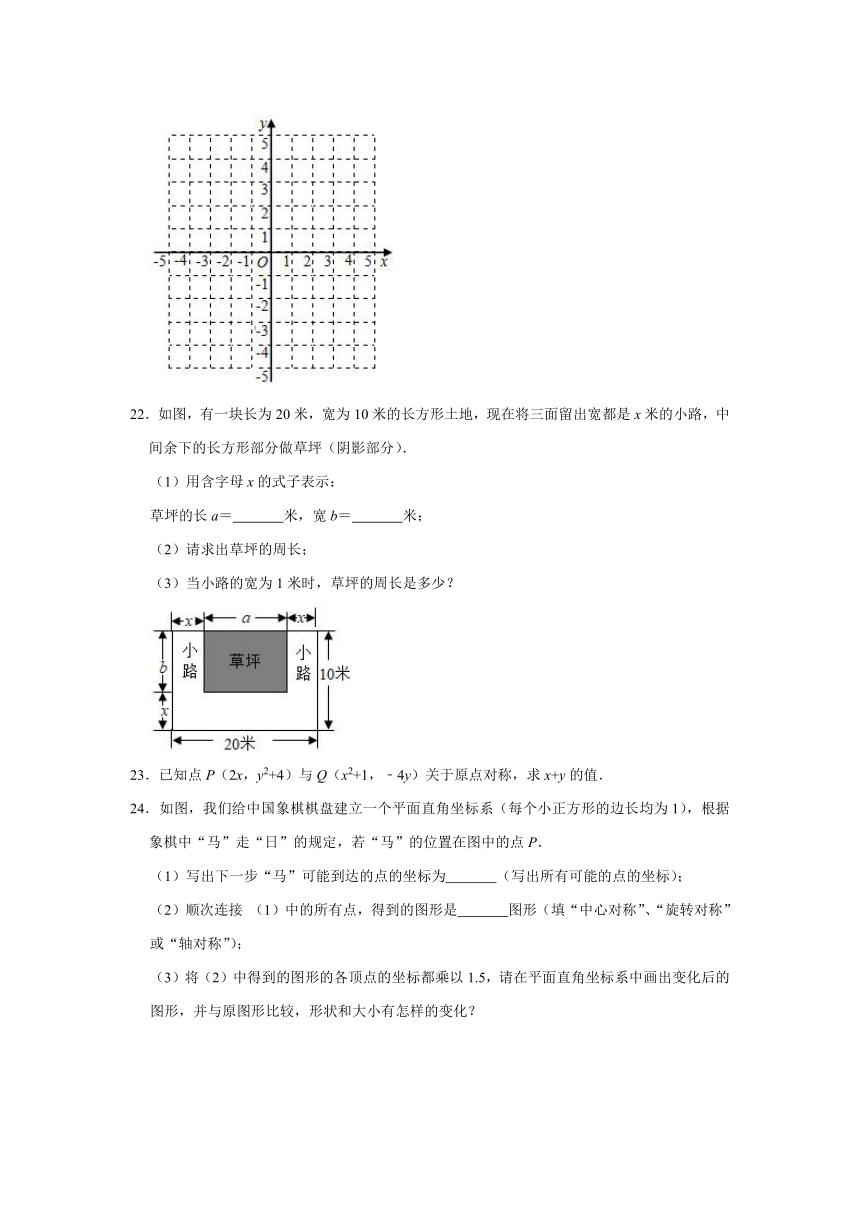
22.如图,有一块长为20米,宽为10米的长方形土地,现在将三面留出宽都是x米的小路,中间余下的长方形部分做草坪(阴影部分).
(1)用含字母x的式子表示:
草坪的长a= 米,宽b= 米;
(2)请求出草坪的周长;
(3)当小路的宽为1米时,草坪的周长是多少?
23.已知点P(2x,y2+4)与Q(x2+1,﹣4y)关于原点对称,求x+y的值.
24.如图,我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形的边长均为1),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点P.
(1)写出下一步“马”可能到达的点的坐标为 (写出所有可能的点的坐标);
(2)顺次连接 (1)中的所有点,得到的图形是 图形(填“中心对称”、“旋转对称”或“轴对称”);
(3)将(2)中得到的图形的各顶点的坐标都乘以1.5,请在平面直角坐标系中画出变化后的图形,并与原图形比较,形状和大小有怎样的变化?
25.如图,点O是等边△ABC内一点,将CO绕点C顺时针旋转60°得到CD,连接OD,AO,BO,AD.
(1)求证:△BCO≌△ACD.
(2)若OA=10,OB=8,OC=6,求∠BOC的度数.
参考答案
一.选择题
1.解:观察图形可知图案C通过平移后可以得到.
故选:C.
2.解:由题意,P′(﹣1+2,0+2),即P′(1,2),在第一象限,
故选:A.
3.解:在Rt△AOB中,∠AOB=90°,AB=2,∠ABO=30°,
∴AO=AB=1,
∴OB=OA=,
∵△OB′C是由∠ABO平移得到,
∴OC=OA=1,B′C=OB=,
∴B′(1,).
故选:C.
4.解:因为经过平移两个图形可变为两个长和宽都相等长方形,所以她们用的铁丝周长一样长.
故选:C.
5.解:A、不是中心对称图形,故本选项不合题意;
B、不是中心对称图形,故本选项不合题意;
C、不是中心对称图形,故本选项不合题意;
D、是中心对称图形,故本选项符合题意.
故选:D.
6.解:∵点P(m2+1,﹣1)与点Q关于原点对称,
∴Q(﹣m2﹣1,1),
∵﹣m2﹣1<0,1>0,
∴点Q一定在第二象限,
故选:B.
7.解:∵△OAB绕点O逆时针旋转80°得到△OCD,
∴∠A=∠C,∠AOC=∠BOD,AB=CD,OB=OD,
∵∠BOD≠90°,
∴BD≠OB.
故选:A.
8.解:∵△OAB是正三角形,
∴∠BOA=60°,
∵OP⊥OB,
∴∠BOP=90°,
∴∠AOP=∠BOA+∠BOP=60°+90°=150°,
即旋转角是150°,
故选:D.
9.解:∵将△ABC绕点A逆时针旋转150°,得到△ADE,
∴∠BAD=150°,AD=AB,∠E=∠ACB,
∵点B,C,D恰好在同一直线上,
∴△BAD是顶角为150°的等腰三角形,
∴∠B=∠BDA,
∴∠B=(180°﹣∠BAD)=15°,
∴∠E=∠ACB=180°﹣∠BAC﹣∠B=180°﹣100°﹣15°=65°,
故选:C.
10.解:∵△EBD是由△ABC旋转得到,
∴BA=BE,∠ABE=60°,AC=DE,
∴△ABE是等边三角形,
∴∠EAB=60°,
∵∠BAD=30°,
∴∠EAD=90°,
∵AE=AB=5,AD=4,
∴DE===,
∴AC=DE=,
故选:D.
二.填空题
11.解:∵△ABC沿BC边平移得到△A1B1C1,
∴BC=B1C1,BB1=CC1,
∵BC1=8,B1C=2,
∴BB1=CC1=,
即平移距离为3,
故答案为:3.
12.解:由题意可得线段AB向左平移3个单位,向上平移了1个单位,
∵A、B两点的坐标分别为(1,0)、(0,2),
∴点A1、B1的坐标分别为(﹣2,1),(﹣3,3),
∴a+b=1﹣3=﹣2,
故答案为:﹣2.
13.解:∵三角形ABC沿AB方向平移AD的长度得到三角形DEF,
∴△ABC≌△DEF,BC=EF=8,
∴BG=BC﹣CG=8﹣3=5,
∵S阴影部分+S△DBG=S△DBG+S梯形BEFG,
∴S阴影部分=S梯形BEFG=(5+8)×6=39.
故答案为39.
14.解:依题意有3a﹣3×1=12,
解得a=5.
故答案为:5.
15.解:由点P(4,﹣6)与点Q(m,n+1)关于原点对称,得
m=﹣4,n+1=6,
所以n=5.
则m+n=﹣4+5=1,
故答案为:1.
16.解:点M(2+m,m﹣1)关于原点的对称点为:(﹣2﹣m,1﹣m),
∵(﹣2﹣m,1﹣m)在第二象限,
∴﹣2﹣m<0,1﹣m>0,
解得:﹣2<m<1.
故答案为:﹣2<m<1.
17.解:作BH⊥PC于H,如图,
∵△ABC为等边三角形,
∴BA=BC,∠ABC=60°,
∴把△ABP绕点B顺时针旋转60°得到△CBD,连接PD,如图,
∴CD=AP=4,BD=BP=2,∠PBD=60°,
∴△PBD为等边三角形,
∴PD=PB=2,∠BPD=60°,
在△PDC中,PC=2,PD=2,CD=4,
∴PC2+PD2=CD2,
∴△PCD为直角三角形,∠CPD=90°,
∴∠BPC=∠BPD+∠CPD=150°,
∴∠BPH=30°,
在Rt△PBH中,∠BPH=30°,PB=2,
∴BH=PB=,PH=BH=3,
∴CH=PC+PH=2+3=5,
在Rt△BCH中,BC2=BH2+CH2=()2+52=28,
∴BC=2,
故答案为:2
18.解:如图,连接AC,AE,BE,
∵EF=2,BF=3,
∴BE===,
∵∠B=60°,AB=BC,
∴△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵将边DA绕点D逆时针旋转60°得到线段DE,
∴AD=AE,∠ADE=60°,
∴△ADE是等边三角形,
∴AE=AD,∠DAE=60°,
∴∠DAE=∠BAC,
∴∠BAE=∠DAC,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS),
∴BE=CD=,
故答案为:.
19.解:如图,连接AD.
在Rt△ADF和Rt△ADC中,
,
∴Rt△ADF≌Rt△ADC(HL),
∴DF=DC,
∵BD=5,BC=4,
∴CD=DF﹣5﹣4=1,
∵EF=BC=4,
∴DE=EF﹣DF=4﹣1=3.
故答案为:3.
20.解:如图,将△ABQ绕点A逆时针旋转60°到△ACP,连接BC,
∴△ABQ≌△ACP,
∴AB=AC,BQ=PC,∠PAQ=∠BAC,
∵△ABC是等边三角形
∴∠PAQ=∠BAC=60°,
∴△ABC是等边三角形,
∵A(1,0),B(3,0),
∴AB=3﹣1=2,
∴C(2,),即点C是定点,
∴当PC最小时,BQ最小,
∴当PC⊥y轴时,PC最小,最小值是2,
∴线段QB长度的最小值为2.
故答案为:2.
三.解答题
21.解:(1)如图,△ABC即为所求作.
(2)如图,△A1B1C1即为所求作.
22.解:(1)由图形所反映的草坪的长a,宽b,路的宽x与原长方形的长20m,宽10m之间关系得,
a=20﹣2x,b=10﹣x,
故答案为:20﹣2x,10﹣x;
(2)由长方形的周长公式得,
[(20﹣2x)+(10﹣x)]×2=60﹣6x(米),
答:长方形的周长为(60﹣6x)米;
(3)当x=1时,60﹣6x=60﹣6=54(米),
答:当小路的宽为1米时,草坪的周长是54米.
23.解:∵点P(2x,y2+4)与Q(x2+1,﹣4y)关于原点对称,
∴x2+1+2x=0,y2+4﹣4y=0,
∴(x+1)2=0,(y﹣2)2=0,
解得:x=﹣1,y=2,
∴x+y=1.
24.解:(1)下一步“马”可能到达的点的坐标:(0,0),(0,2),(1,3),(3,3),(4,2),(4,0);
(2)连线可以看出得的图形为轴对称;
(3)将(2)中得到的图形的各顶点的坐标都乘以1.5,如图所示,与原图形比较,形状不变,图形变大了.
故答案为:(1)(0,0),(0,2),(1,3),(3,3),(4,2),(4,0);(2)轴对称.
25.(1)证明:∵CO绕点C顺时针旋转60°得到CD,
∴CO=CD,∠OCD=60°,
∵△ABC是等边三角形,
∴CA=CB,∠BCA=60°,
∴∠BCA=∠OCD,
∴∠BCO=∠ACD,
在△BCO和△ACD中,
,
∴△BCO≌△ACD(SAS).
(2)解:∵CO=CD,∠OCD=60°,
∴△OCD是等边三角形,
∴OD=OC=6.∠ODC=60°,
∵△BCO≌△ACD,
∴AD=OB=8,∠BOC=∠ADC,
∵OA=10,
∴OA2=AD2+OD2,
∴∠ADO=90°,
∴∠ADC=∠ADO+∠CDO=150°,
∴∠BOC=∠ADC=150°.
一.选择题
1.下列各组图形可以通过平移互相得到的是( )
A. B.
C. D.
2.在平面直角坐标系中,将点P(﹣1,0)向右平移2个单位,再向上平移2个单位,得到点P′,则点P′在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.如图,已知一个斜边长为2的直角三角板的直角顶点与原点重合,两直角边分别落在两个坐标轴上.现将该三角板向右平移使点A与点O重合,得到△OCB′,则点B的对应点B′的坐标是( )
A.(1,0) B.(,) C.(1,) D.(﹣1,)
4.在手工制作课上,张华和李丽用铁丝制作楼梯模型,如图所示,则她们用的铁丝周长( )
A.张华的长 B.李丽的长 C.一样长 D.不能确定
5.下列图形中,是中心对称图形的是( )
A. B. C. D.
6.已知点P(m2+1,﹣1)与点Q关于原点对称,则点Q一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.如图,把△OAB绕点O逆时针旋转80°,得到△OCD,则下列结论错误的是( )
A.BD=OB B.AB=CD C.∠AOC=∠BOD D.∠A=∠C
8.如图,已知△OAB是正三角形,OP⊥OB,OP=OA,将△OAB绕点O按顺时针方向旋转,使得OA与OP重合,得到△OPQ,则旋转的角度是( )
A.60° B.90° C.120° D.150°
9.如图,△ABC中∠BAC=100°,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B、C、D恰好在同一直线上,则∠E的度数为( )
A.50° B.75° C.65° D.60°
10.如图,四边形ABCD中,∠DAB=30°,连接AC,将△ABC绕点B逆时针旋转60°,点C的对应点与点D重合,得到△EBD,若AB=5,AD=4,则点AC的长度为( )
A.5 B.6 C. D.
二.填空题
11.如图所示,将△ABC沿BC边平移得到△A1B1C1,若BC1=8,B1C=2,则平移距离为 .
12.A、B两点的坐标分别为(1,0)、(0,2),落将线段AB平移至A1B1,点A1、B1的坐标分别为(﹣2,a),(b,3),则a+b= .
13.如图,在三角形ABC中,∠ABC=90°,将三角形ABC沿AB方向平移AD的长度得到三角形DEF.已EF=8,BE=6,CG=3.则图中阴影部分的面积是 .
14.如图,有一块长为a米,宽为3米的长方形地,中间阴影部分是一条小路,空白部分为草地,小路的左边线向右平移1米能得到它的右边线,若草地的面积为12米2,则a= .
15.在平面直角坐标系中,点P(4,﹣6)与点Q(m,n+1)关于原点对称,那么m+n= .
16.已知点M(2+m,m﹣1)关于原点的对称点在第二象限,则m的取值范围是 .
17.如图,P是等边△ABC内一点,PA=4,PB=2,PC=2,则△ABC的边长为 .
18.如图,四边形ABCD中,∠B=60°,AB=BC,将边DA绕点D逆时针旋转60°得到线段DE,过点E做EF⊥BC,垂足为F,若EF=2,BF=3,则线段CD的长是 .
19.如图,在△ABC中,∠ACB=90°,将△ABC绕点A逆时针旋转到△AEF,延长BC交EF于点D,若BD=5,BC=4,则DE= .
20.如图,在平面直角坐标系xOy中,A(1,0),B(3,0),点P为y轴正半轴上的一个动点,以线段PA为边在PA的右上方作等边△APQ,连接QB,在点P运动的过程中,线段QB长度的最小值为 .
三.解答题
21.已知在平面直角坐标系中,△ABC三个顶点的坐标分别为:A(﹣3,﹣1),B(﹣2,﹣4),C(1,﹣3).
(1)作出△ABC;
(2)若将△ABC向上平移3个单位后再向右平移2个单位得到△A1B1C1,请作出△A1B1C1.
22.如图,有一块长为20米,宽为10米的长方形土地,现在将三面留出宽都是x米的小路,中间余下的长方形部分做草坪(阴影部分).
(1)用含字母x的式子表示:
草坪的长a= 米,宽b= 米;
(2)请求出草坪的周长;
(3)当小路的宽为1米时,草坪的周长是多少?
23.已知点P(2x,y2+4)与Q(x2+1,﹣4y)关于原点对称,求x+y的值.
24.如图,我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形的边长均为1),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点P.
(1)写出下一步“马”可能到达的点的坐标为 (写出所有可能的点的坐标);
(2)顺次连接 (1)中的所有点,得到的图形是 图形(填“中心对称”、“旋转对称”或“轴对称”);
(3)将(2)中得到的图形的各顶点的坐标都乘以1.5,请在平面直角坐标系中画出变化后的图形,并与原图形比较,形状和大小有怎样的变化?
25.如图,点O是等边△ABC内一点,将CO绕点C顺时针旋转60°得到CD,连接OD,AO,BO,AD.
(1)求证:△BCO≌△ACD.
(2)若OA=10,OB=8,OC=6,求∠BOC的度数.
参考答案
一.选择题
1.解:观察图形可知图案C通过平移后可以得到.
故选:C.
2.解:由题意,P′(﹣1+2,0+2),即P′(1,2),在第一象限,
故选:A.
3.解:在Rt△AOB中,∠AOB=90°,AB=2,∠ABO=30°,
∴AO=AB=1,
∴OB=OA=,
∵△OB′C是由∠ABO平移得到,
∴OC=OA=1,B′C=OB=,
∴B′(1,).
故选:C.
4.解:因为经过平移两个图形可变为两个长和宽都相等长方形,所以她们用的铁丝周长一样长.
故选:C.
5.解:A、不是中心对称图形,故本选项不合题意;
B、不是中心对称图形,故本选项不合题意;
C、不是中心对称图形,故本选项不合题意;
D、是中心对称图形,故本选项符合题意.
故选:D.
6.解:∵点P(m2+1,﹣1)与点Q关于原点对称,
∴Q(﹣m2﹣1,1),
∵﹣m2﹣1<0,1>0,
∴点Q一定在第二象限,
故选:B.
7.解:∵△OAB绕点O逆时针旋转80°得到△OCD,
∴∠A=∠C,∠AOC=∠BOD,AB=CD,OB=OD,
∵∠BOD≠90°,
∴BD≠OB.
故选:A.
8.解:∵△OAB是正三角形,
∴∠BOA=60°,
∵OP⊥OB,
∴∠BOP=90°,
∴∠AOP=∠BOA+∠BOP=60°+90°=150°,
即旋转角是150°,
故选:D.
9.解:∵将△ABC绕点A逆时针旋转150°,得到△ADE,
∴∠BAD=150°,AD=AB,∠E=∠ACB,
∵点B,C,D恰好在同一直线上,
∴△BAD是顶角为150°的等腰三角形,
∴∠B=∠BDA,
∴∠B=(180°﹣∠BAD)=15°,
∴∠E=∠ACB=180°﹣∠BAC﹣∠B=180°﹣100°﹣15°=65°,
故选:C.
10.解:∵△EBD是由△ABC旋转得到,
∴BA=BE,∠ABE=60°,AC=DE,
∴△ABE是等边三角形,
∴∠EAB=60°,
∵∠BAD=30°,
∴∠EAD=90°,
∵AE=AB=5,AD=4,
∴DE===,
∴AC=DE=,
故选:D.
二.填空题
11.解:∵△ABC沿BC边平移得到△A1B1C1,
∴BC=B1C1,BB1=CC1,
∵BC1=8,B1C=2,
∴BB1=CC1=,
即平移距离为3,
故答案为:3.
12.解:由题意可得线段AB向左平移3个单位,向上平移了1个单位,
∵A、B两点的坐标分别为(1,0)、(0,2),
∴点A1、B1的坐标分别为(﹣2,1),(﹣3,3),
∴a+b=1﹣3=﹣2,
故答案为:﹣2.
13.解:∵三角形ABC沿AB方向平移AD的长度得到三角形DEF,
∴△ABC≌△DEF,BC=EF=8,
∴BG=BC﹣CG=8﹣3=5,
∵S阴影部分+S△DBG=S△DBG+S梯形BEFG,
∴S阴影部分=S梯形BEFG=(5+8)×6=39.
故答案为39.
14.解:依题意有3a﹣3×1=12,
解得a=5.
故答案为:5.
15.解:由点P(4,﹣6)与点Q(m,n+1)关于原点对称,得
m=﹣4,n+1=6,
所以n=5.
则m+n=﹣4+5=1,
故答案为:1.
16.解:点M(2+m,m﹣1)关于原点的对称点为:(﹣2﹣m,1﹣m),
∵(﹣2﹣m,1﹣m)在第二象限,
∴﹣2﹣m<0,1﹣m>0,
解得:﹣2<m<1.
故答案为:﹣2<m<1.
17.解:作BH⊥PC于H,如图,
∵△ABC为等边三角形,
∴BA=BC,∠ABC=60°,
∴把△ABP绕点B顺时针旋转60°得到△CBD,连接PD,如图,
∴CD=AP=4,BD=BP=2,∠PBD=60°,
∴△PBD为等边三角形,
∴PD=PB=2,∠BPD=60°,
在△PDC中,PC=2,PD=2,CD=4,
∴PC2+PD2=CD2,
∴△PCD为直角三角形,∠CPD=90°,
∴∠BPC=∠BPD+∠CPD=150°,
∴∠BPH=30°,
在Rt△PBH中,∠BPH=30°,PB=2,
∴BH=PB=,PH=BH=3,
∴CH=PC+PH=2+3=5,
在Rt△BCH中,BC2=BH2+CH2=()2+52=28,
∴BC=2,
故答案为:2
18.解:如图,连接AC,AE,BE,
∵EF=2,BF=3,
∴BE===,
∵∠B=60°,AB=BC,
∴△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵将边DA绕点D逆时针旋转60°得到线段DE,
∴AD=AE,∠ADE=60°,
∴△ADE是等边三角形,
∴AE=AD,∠DAE=60°,
∴∠DAE=∠BAC,
∴∠BAE=∠DAC,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS),
∴BE=CD=,
故答案为:.
19.解:如图,连接AD.
在Rt△ADF和Rt△ADC中,
,
∴Rt△ADF≌Rt△ADC(HL),
∴DF=DC,
∵BD=5,BC=4,
∴CD=DF﹣5﹣4=1,
∵EF=BC=4,
∴DE=EF﹣DF=4﹣1=3.
故答案为:3.
20.解:如图,将△ABQ绕点A逆时针旋转60°到△ACP,连接BC,
∴△ABQ≌△ACP,
∴AB=AC,BQ=PC,∠PAQ=∠BAC,
∵△ABC是等边三角形
∴∠PAQ=∠BAC=60°,
∴△ABC是等边三角形,
∵A(1,0),B(3,0),
∴AB=3﹣1=2,
∴C(2,),即点C是定点,
∴当PC最小时,BQ最小,
∴当PC⊥y轴时,PC最小,最小值是2,
∴线段QB长度的最小值为2.
故答案为:2.
三.解答题
21.解:(1)如图,△ABC即为所求作.
(2)如图,△A1B1C1即为所求作.
22.解:(1)由图形所反映的草坪的长a,宽b,路的宽x与原长方形的长20m,宽10m之间关系得,
a=20﹣2x,b=10﹣x,
故答案为:20﹣2x,10﹣x;
(2)由长方形的周长公式得,
[(20﹣2x)+(10﹣x)]×2=60﹣6x(米),
答:长方形的周长为(60﹣6x)米;
(3)当x=1时,60﹣6x=60﹣6=54(米),
答:当小路的宽为1米时,草坪的周长是54米.
23.解:∵点P(2x,y2+4)与Q(x2+1,﹣4y)关于原点对称,
∴x2+1+2x=0,y2+4﹣4y=0,
∴(x+1)2=0,(y﹣2)2=0,
解得:x=﹣1,y=2,
∴x+y=1.
24.解:(1)下一步“马”可能到达的点的坐标:(0,0),(0,2),(1,3),(3,3),(4,2),(4,0);
(2)连线可以看出得的图形为轴对称;
(3)将(2)中得到的图形的各顶点的坐标都乘以1.5,如图所示,与原图形比较,形状不变,图形变大了.
故答案为:(1)(0,0),(0,2),(1,3),(3,3),(4,2),(4,0);(2)轴对称.
25.(1)证明:∵CO绕点C顺时针旋转60°得到CD,
∴CO=CD,∠OCD=60°,
∵△ABC是等边三角形,
∴CA=CB,∠BCA=60°,
∴∠BCA=∠OCD,
∴∠BCO=∠ACD,
在△BCO和△ACD中,
,
∴△BCO≌△ACD(SAS).
(2)解:∵CO=CD,∠OCD=60°,
∴△OCD是等边三角形,
∴OD=OC=6.∠ODC=60°,
∵△BCO≌△ACD,
∴AD=OB=8,∠BOC=∠ADC,
∵OA=10,
∴OA2=AD2+OD2,
∴∠ADO=90°,
∴∠ADC=∠ADO+∠CDO=150°,
∴∠BOC=∠ADC=150°.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
