第十八章 平行四边形 单元测试题(Word版 含答案)
文档属性
| 名称 | 第十八章 平行四边形 单元测试题(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 317.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 00:00:00 | ||
图片预览


文档简介
第十八章 平行四边形 单元测试题
一、选择题(30分)
1.已知平行四边形false,对角线false、false,则该平行四边形四条边中最长边a的取值范围是( )
A.false B.false C.false D.false
2.若平行四边形中两个内角的度数比为1:5 ,则其中较大的角是( )
A.60° B.120° C.135° D.150°
3.菱形和矩形都具有的性质是( )
A.对角线互相垂直
B.对角线相等
C.对角线平分一组对角
D.对角线互相平分并且是中心对称图形
4.下列说法①两组对边分别平行的四边形是平行四边形;②平行四边形的对角线互相平分③两组对边分别相等的四边形是平行四边形;④平行四边形的每组对边平行且相等;⑤两条对角线互相平分的四边形是平行四边形;属于平行四边形判定方法的有( )
A.5个 B.4个 C.3个 D.2个
5.下列命题中,正确的是( )
A.邻边相等的四边形是菱形 B.有一个角是直角的四边形是矩形
C.四个角相等的菱形是正方形 D.两条对角线互相垂直且相等的四边形是正方形
6.如图所示,正方形false,点false在正方形对角线false上,且false,则false的度数为( )
A.false B.false C.false D.false
7.如图,false的对角线false,false交于点O,false,false,false,那么false的长为( )
A.false B.false C.3 D.4
8.如图,在正方形false中,对角线false与false相交于点false,图中有( )个等腰直角三角形.
A.2 B.4 C.8 D.16
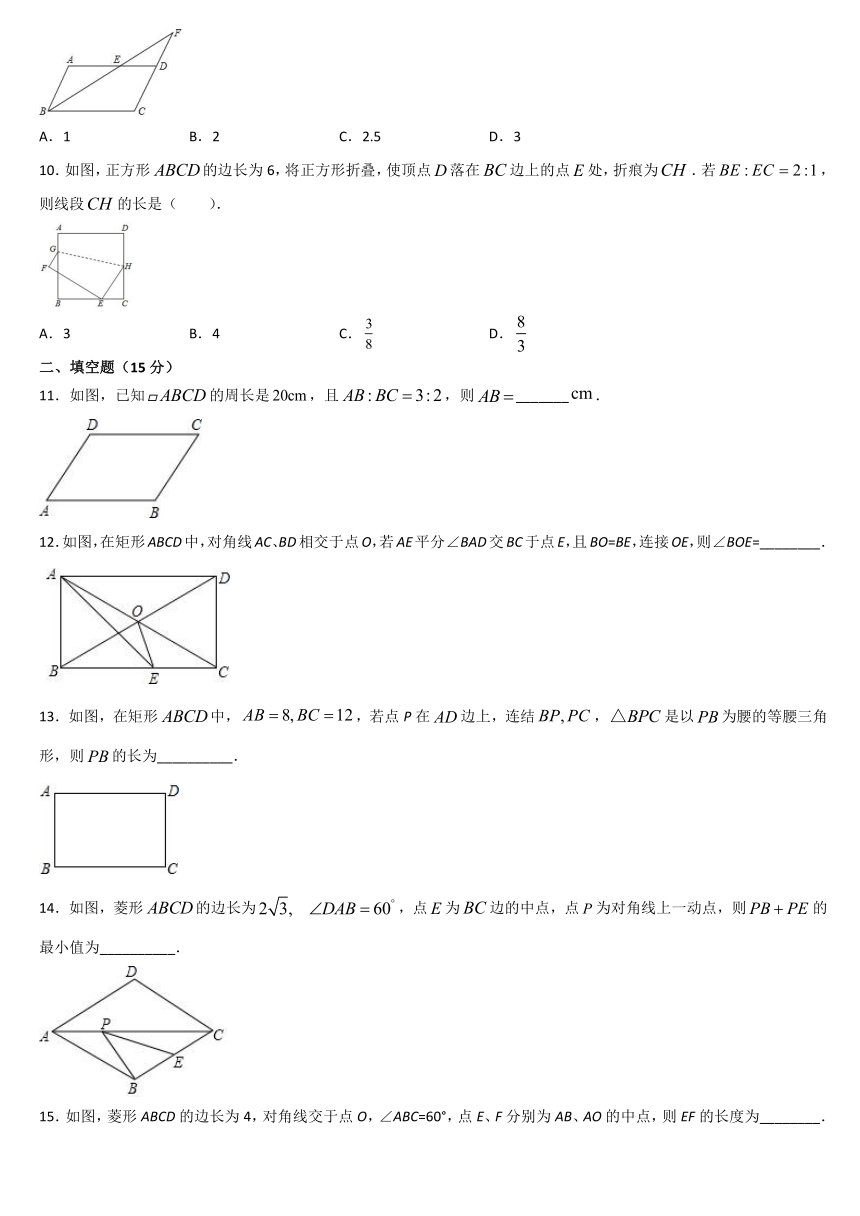
9.如图,在false中,false,false,false的平分线交false于E,交false的延长线于点F,则false( )
A.1 B.2 C.2.5 D.3
10.如图,正方形false的边长为6,将正方形折叠,使顶点false落在false边上的点false处,折痕为false.若false,则线段false的长是( ).
A.3 B.4 C.false D.false
二、填空题(15分)
11.如图,已知false的周长是false,且false,则false_______false.
12.如图,在矩形ABCD中,对角线AC、BD相交于点O,若AE平分∠BAD交BC于点E,且BO=BE,连接OE,则∠BOE=________.
13.如图,在矩形false中,false,若点P在false边上,连结false,false是以false为腰的等腰三角形,则false的长为__________.
14.如图,菱形false的边长为false,点false为false边的中点,点false为对角线上一动点,则false的最小值为__________.
15.如图,菱形ABCD的边长为4,对角线交于点O,∠ABC=60°,点E、F分别为AB、AO的中点,则EF的长度为________.
三、解答题(75分)
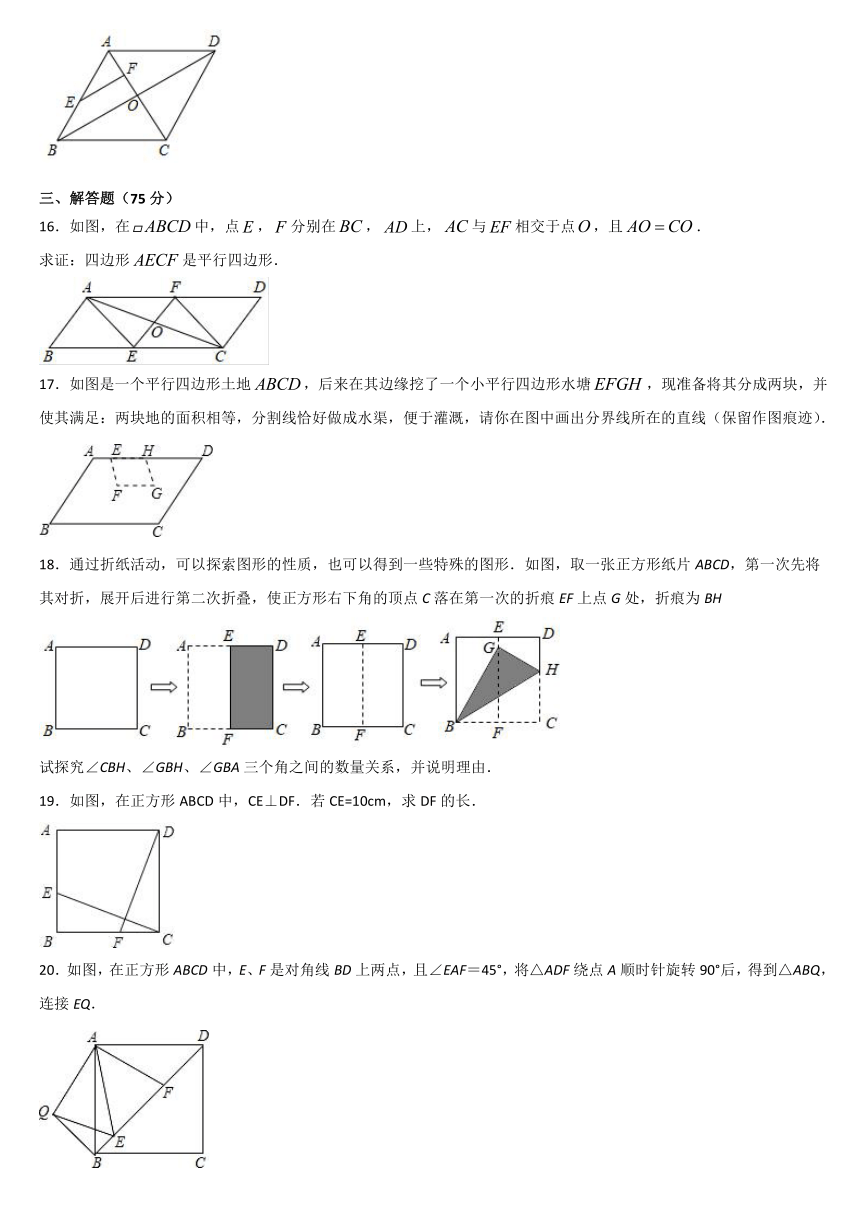
16.如图,在false中,点false,false分别在false,false上,false与false相交于点false,且false.
求证:四边形false是平行四边形.
17.如图是一个平行四边形土地false,后来在其边缘挖了一个小平行四边形水塘false,现准备将其分成两块,并使其满足:两块地的面积相等,分割线恰好做成水渠,便于灌溉,请你在图中画出分界线所在的直线(保留作图痕迹).
18.通过折纸活动,可以探索图形的性质,也可以得到一些特殊的图形.如图,取一张正方形纸片ABCD,第一次先将其对折,展开后进行第二次折叠,使正方形右下角的顶点C落在第一次的折痕EF上点G处,折痕为BH
试探究∠CBH、∠GBH、∠GBA三个角之间的数量关系,并说明理由.
19.如图,在正方形ABCD中,CE⊥DF.若CE=10cm,求DF的长.
20.如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ.
(1)求证:EA是∠QED的平分线;
(2)已知BE=1,DF=3,求EF的长.
21.如图所示,把一张矩形ABDC纸片沿对角线BC折叠,重合部分false是什么图形,试说明理由;若AB=4,BD=8,求AF的长.
22.如图,将长方形形false(false)沿折叠后,点false落在点false处,且false交false于点false,若false,false.
(1)求false的长.
(2)点false到false边上的距离.
23.在RtfalseABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)证明四边形ADCF是菱形;
(2)若AC=4,AB=5,求菱形ADCF的面积.
【参考答案】
1.B 2.D 3.D 4.C 5.C 6.A 7.D 8.C 9.B 10.D
11.6
12.75°
13.10或12
14.3
15.false
16.证明:∵四边形false是平行四边形,
∴false,
∴false,
在false和false中,false,
∴false(false)
∴false,
又∵false,
∴四边形false是平行四边形.
17.解:作两个平行四边形的两对对角线,其交点分别为M、N.即AC与BD交于点N,EG与FH交于点M,
连接MN,直线MN即为所求的分割线.
因为,过平行四边形对角线交点的直线等分其面积.
如图:
18.∠CBH=∠GBH=∠GBA.
理由:连接CG,
由第一次折叠知点B、C关于EF对称,
∴EF垂直平分BC,
∴BG=CG,
由第二次折叠知△BCH≌△BGH,
∴BG=BC,
∴BG=CG=BC,
∴△BCG是等边三角形,
∴∠CBG=60°,
∵△BCH≌△BGH,
∴∠CBH=∠GBH=30°,
∵∠ABC=90°,
∴false,
∴∠CBH=∠GBH=∠GBA.
19.解:∵CE⊥DF,
∴∠CDF+∠DCE=90°,
又∵∠DCB=∠DCE+∠BCE=90°,
∴∠CDF=∠BCE,
在正方形ABCD中
又∵BC=CD,∠EBC=∠FCD=90°,
∴△BCE≌△CDF(ASA),
∴CE=DF,
∵CE=10cm,
∴DF=10cm.
20.证明:(1)∵将△ADF绕点A顺时针旋转90°后,得到△ABQ,
∴QB=DF,AQ=AF,∠BAQ=∠DAF,
∵∠EAF=45°,
∴∠DAF+∠BAE=45°,
∴∠QAE=45°,
∴∠QAE=∠FAE,
在△AQE和△AFE中,
false,
∴△AQE≌△AFE(SAS),
∴∠AEQ=∠AEF,
∴EA是∠QED的平分线;
(2)由(1)得△AQE≌△AFE,
∴QE=EF,∠ADF=∠ABQ,
∵四边形ABCD是正方形,
∴∠ADB=∠ABD=45°,
∴∠ABQ=45°,
∴∠QBE=∠ABQ+∠ABD=90°,
在Rt△QBE中,QB2+BE2=QE2,
又∵QB=DF,
∴EF2=BE2+DF2=1+9=10,
∴EF=false.
21解:重叠部分△BCF为等腰三角形,
理由如下:由折叠及矩形的性质可知∠CBD=∠FBC,AC∥BD,
∴∠FCB=∠CBD,
∴∠FBC=∠FCB,
∴BF=CF,
∴重叠部分△BCF为等腰三角形,
设AF=x,则BF=CF=8-x,
在直角三角形ABF中,由勾股定理得AB2+AF2=BF2,即42+x2=(8-x)2
解得:AF=x=3.
22.解:(1)∵四边形是长方形,
∴false,false,false,false,
∴false,
由折叠性质得:false,
∴false,
∴false,
设false,则false,
在false中,由勾股定理得:false,
即:false
解得:false,
∴false.
(2)设false到false边上的距离为false,
由折叠的性质得:false,false,false,
false,
∴false,
∴false,
解得:false,
∴false到false边上的距离为false.
23.(1)证明:如图,∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中,
false,
∴△AFE≌△DBE(AAS);
∴AF=DB.
∵DB=DC,
∴AF=CD,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=DC=falseBC,
∴四边形ADCF是菱形;
(2)解:连接DF,
∵AF∥BC,AF=BD,
∴四边形ABDF是平行四边形,
∴DF=AB=5,
∵四边形ADCF是菱形,
∴S=falseAC?DF=10.
一、选择题(30分)
1.已知平行四边形false,对角线false、false,则该平行四边形四条边中最长边a的取值范围是( )
A.false B.false C.false D.false
2.若平行四边形中两个内角的度数比为1:5 ,则其中较大的角是( )
A.60° B.120° C.135° D.150°
3.菱形和矩形都具有的性质是( )
A.对角线互相垂直
B.对角线相等
C.对角线平分一组对角
D.对角线互相平分并且是中心对称图形
4.下列说法①两组对边分别平行的四边形是平行四边形;②平行四边形的对角线互相平分③两组对边分别相等的四边形是平行四边形;④平行四边形的每组对边平行且相等;⑤两条对角线互相平分的四边形是平行四边形;属于平行四边形判定方法的有( )
A.5个 B.4个 C.3个 D.2个
5.下列命题中,正确的是( )
A.邻边相等的四边形是菱形 B.有一个角是直角的四边形是矩形
C.四个角相等的菱形是正方形 D.两条对角线互相垂直且相等的四边形是正方形
6.如图所示,正方形false,点false在正方形对角线false上,且false,则false的度数为( )
A.false B.false C.false D.false
7.如图,false的对角线false,false交于点O,false,false,false,那么false的长为( )
A.false B.false C.3 D.4
8.如图,在正方形false中,对角线false与false相交于点false,图中有( )个等腰直角三角形.
A.2 B.4 C.8 D.16
9.如图,在false中,false,false,false的平分线交false于E,交false的延长线于点F,则false( )
A.1 B.2 C.2.5 D.3
10.如图,正方形false的边长为6,将正方形折叠,使顶点false落在false边上的点false处,折痕为false.若false,则线段false的长是( ).
A.3 B.4 C.false D.false
二、填空题(15分)
11.如图,已知false的周长是false,且false,则false_______false.
12.如图,在矩形ABCD中,对角线AC、BD相交于点O,若AE平分∠BAD交BC于点E,且BO=BE,连接OE,则∠BOE=________.
13.如图,在矩形false中,false,若点P在false边上,连结false,false是以false为腰的等腰三角形,则false的长为__________.
14.如图,菱形false的边长为false,点false为false边的中点,点false为对角线上一动点,则false的最小值为__________.
15.如图,菱形ABCD的边长为4,对角线交于点O,∠ABC=60°,点E、F分别为AB、AO的中点,则EF的长度为________.
三、解答题(75分)
16.如图,在false中,点false,false分别在false,false上,false与false相交于点false,且false.
求证:四边形false是平行四边形.
17.如图是一个平行四边形土地false,后来在其边缘挖了一个小平行四边形水塘false,现准备将其分成两块,并使其满足:两块地的面积相等,分割线恰好做成水渠,便于灌溉,请你在图中画出分界线所在的直线(保留作图痕迹).
18.通过折纸活动,可以探索图形的性质,也可以得到一些特殊的图形.如图,取一张正方形纸片ABCD,第一次先将其对折,展开后进行第二次折叠,使正方形右下角的顶点C落在第一次的折痕EF上点G处,折痕为BH
试探究∠CBH、∠GBH、∠GBA三个角之间的数量关系,并说明理由.
19.如图,在正方形ABCD中,CE⊥DF.若CE=10cm,求DF的长.
20.如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ.
(1)求证:EA是∠QED的平分线;
(2)已知BE=1,DF=3,求EF的长.
21.如图所示,把一张矩形ABDC纸片沿对角线BC折叠,重合部分false是什么图形,试说明理由;若AB=4,BD=8,求AF的长.
22.如图,将长方形形false(false)沿折叠后,点false落在点false处,且false交false于点false,若false,false.
(1)求false的长.
(2)点false到false边上的距离.
23.在RtfalseABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)证明四边形ADCF是菱形;
(2)若AC=4,AB=5,求菱形ADCF的面积.
【参考答案】
1.B 2.D 3.D 4.C 5.C 6.A 7.D 8.C 9.B 10.D
11.6
12.75°
13.10或12
14.3
15.false
16.证明:∵四边形false是平行四边形,
∴false,
∴false,
在false和false中,false,
∴false(false)
∴false,
又∵false,
∴四边形false是平行四边形.
17.解:作两个平行四边形的两对对角线,其交点分别为M、N.即AC与BD交于点N,EG与FH交于点M,
连接MN,直线MN即为所求的分割线.
因为,过平行四边形对角线交点的直线等分其面积.
如图:
18.∠CBH=∠GBH=∠GBA.
理由:连接CG,
由第一次折叠知点B、C关于EF对称,
∴EF垂直平分BC,
∴BG=CG,
由第二次折叠知△BCH≌△BGH,
∴BG=BC,
∴BG=CG=BC,
∴△BCG是等边三角形,
∴∠CBG=60°,
∵△BCH≌△BGH,
∴∠CBH=∠GBH=30°,
∵∠ABC=90°,
∴false,
∴∠CBH=∠GBH=∠GBA.
19.解:∵CE⊥DF,
∴∠CDF+∠DCE=90°,
又∵∠DCB=∠DCE+∠BCE=90°,
∴∠CDF=∠BCE,
在正方形ABCD中
又∵BC=CD,∠EBC=∠FCD=90°,
∴△BCE≌△CDF(ASA),
∴CE=DF,
∵CE=10cm,
∴DF=10cm.
20.证明:(1)∵将△ADF绕点A顺时针旋转90°后,得到△ABQ,
∴QB=DF,AQ=AF,∠BAQ=∠DAF,
∵∠EAF=45°,
∴∠DAF+∠BAE=45°,
∴∠QAE=45°,
∴∠QAE=∠FAE,
在△AQE和△AFE中,
false,
∴△AQE≌△AFE(SAS),
∴∠AEQ=∠AEF,
∴EA是∠QED的平分线;
(2)由(1)得△AQE≌△AFE,
∴QE=EF,∠ADF=∠ABQ,
∵四边形ABCD是正方形,
∴∠ADB=∠ABD=45°,
∴∠ABQ=45°,
∴∠QBE=∠ABQ+∠ABD=90°,
在Rt△QBE中,QB2+BE2=QE2,
又∵QB=DF,
∴EF2=BE2+DF2=1+9=10,
∴EF=false.
21解:重叠部分△BCF为等腰三角形,
理由如下:由折叠及矩形的性质可知∠CBD=∠FBC,AC∥BD,
∴∠FCB=∠CBD,
∴∠FBC=∠FCB,
∴BF=CF,
∴重叠部分△BCF为等腰三角形,
设AF=x,则BF=CF=8-x,
在直角三角形ABF中,由勾股定理得AB2+AF2=BF2,即42+x2=(8-x)2
解得:AF=x=3.
22.解:(1)∵四边形是长方形,
∴false,false,false,false,
∴false,
由折叠性质得:false,
∴false,
∴false,
设false,则false,
在false中,由勾股定理得:false,
即:false
解得:false,
∴false.
(2)设false到false边上的距离为false,
由折叠的性质得:false,false,false,
false,
∴false,
∴false,
解得:false,
∴false到false边上的距离为false.
23.(1)证明:如图,∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中,
false,
∴△AFE≌△DBE(AAS);
∴AF=DB.
∵DB=DC,
∴AF=CD,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=DC=falseBC,
∴四边形ADCF是菱形;
(2)解:连接DF,
∵AF∥BC,AF=BD,
∴四边形ABDF是平行四边形,
∴DF=AB=5,
∵四边形ADCF是菱形,
∴S=falseAC?DF=10.
