苏科版七年级下册数学10.1二元一次方程课件 (19张ppt)
文档属性
| 名称 | 苏科版七年级下册数学10.1二元一次方程课件 (19张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 326.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-29 00:00:00 | ||
图片预览






文档简介
教学目标
(一)知识目标
1、经历分析实际问题中数量关系的过程,进一步体会方程是刻画现实世界的有效的数学模型。
2、了解二元一次方程及其解的概念。
(二)能力目标
1、会判断一组数是否是某个二元一次方程的解。
2、经历现实情境的问题研究,进一步培养学生的观察、比较、分析的能力。
(三)情感目标
1、通过对实际问题的分析,使学生进一步体会方程是刻画现实世界的有效数学模型,培养学生良好的数学应用意识。
2、培养合作交流和数学“化归”思想,体会二元一次方程的实际应用价值。
单击此处编辑母版副标题样式
单击此处编辑母版标题样式
生活中一切问题都可以转化为数学问题,
一切数学问题都可以转化为代数问题,
而一切代数问题又可以转化为方程,
因此,一旦解决了方程问题,
一切问题就将迎刃而解.
_____ 笛卡儿
两
数
差
为
7
两
数
和
为
9
不考虑牌的花色情况
§10.1
二元一次方程
x-1 +9y=0
请判断下列方程是否为二元一次方程,并说明理由。
(3)xy+2x+1=0
(1)2x+y+z=1
(2) x -5y=20
2
(4) +9y=0
x
1
含有两个未知数,并且含未知数的项的次数都是1的方程叫做二元一次方程.
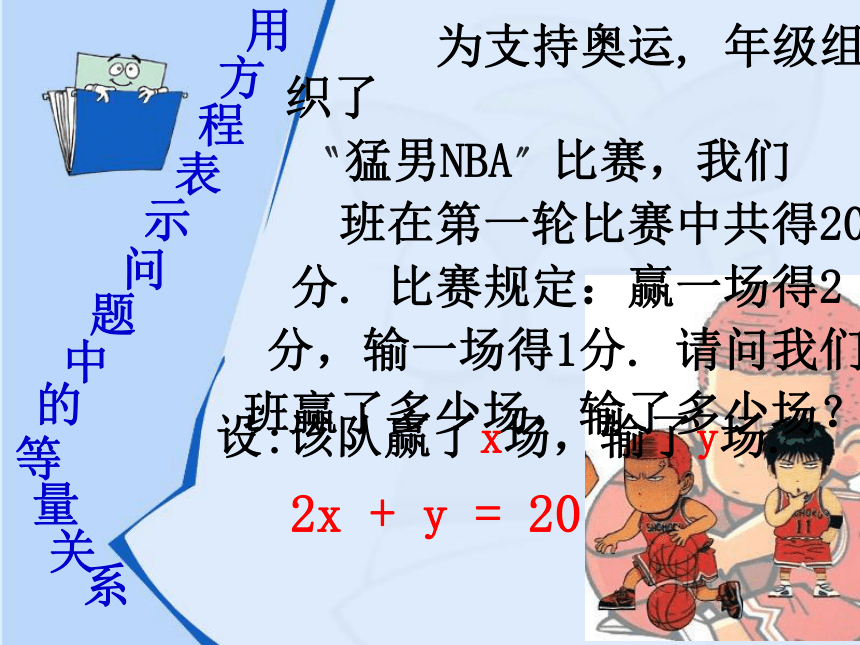
为支持奥运, 年级组织了
〝猛男NBA〞比赛,我们
班在第一轮比赛中共得20
分. 比赛规定:赢一场得2
分,输一场得1分. 请问我们
班赢了多少场,输了多少场?
系
用
方
程
表
题
问
中
示
的
等
量
关
设:该队赢了x场,输了y场.
2x + y = 20
探究一:满足方程2x +y =20,且符合问题实际意义的x、y的 值有哪些?把它们填入下表.
y
X
适合二元一次方程的一对未知数的值叫做这个二元一次方程的一个解.
1
2
3
4
5
6
7
8
9
10
0
20
18
16
14
12
10
8
6
4
2
0
解:因为当x=2,y=18时,
例1、判断: x=2
y=18
是否是方程2x+y=20的解?
所以 不是方程2x+y=20的解
x=2 y=18
左边=2×2+1×18=22≠右边
探究二: 若不考虑实际背景,
二元一次方程2x+y=20,
有多少个解呢?
注意:一般地,一个二元一次方程的解不唯一,常常有无数个.
y=20 - 2x
再任意取x的值代入,
求出相应的y值
用含有一个未知数的代
数式表示另一个未知数
2x+y=20
原方程的解
注意:
1、也可用含
y的代数式
表示x……
2、前提是没
有实际背景
的限制
思考: 二元一次方程的解和一元一次方程的解有什么区别?
解的形式
解的个数
二元一次方程 的解
一元一次方程 的解
一个
无数个
一个未知数的
值 x=m
一对未知数的值
x=m
y=n
探究三:某球员在〝猛
男NBA〞的一场比赛中
共得35分, 其中罚球得10
分。请问他投中 了多少个
两分球?多少个三分球?
设:投中x个两分球,y个三分球.
则2x+3y=35-10
元
次
程
是
画
实
界
效
型
的
二
一
方
也
刻
现
世
有
模
即2x+3y=25
三分球y
两分球x
2x+3y=25
请你设计一张表格,列出
这名球员投中的两分球和
三分球的各种情况.
元
次
程
是
画
实
界
效
型
的
二
一
方
也
刻
现
世
有
模
11
1
8
3
5
2
5
7
根据所列表格回答:
(1)该球员最多投中了多少个三分球?
(2)该球员最多投中了多少个球?
7
5
3
1
三分球y
两分球x
11 8 5 2
根据所列表格回答:
(3)如果该球员投中了10个球,
那么其中几个两分球?几个三分球?
7
5
3
1
三分球y
两分球x
11 8 5 2
这节课你学到了什么?
课后反思
1、想想“用二元一次方程表达实际问题”与“用一元一次方程表达实际问题”有何异同?
2、用二元一次方程表达实际问题的关键是什么?
两
数
差
为
7
两
数
和
为
9
考虑牌的花色情况
(一)知识目标
1、经历分析实际问题中数量关系的过程,进一步体会方程是刻画现实世界的有效的数学模型。
2、了解二元一次方程及其解的概念。
(二)能力目标
1、会判断一组数是否是某个二元一次方程的解。
2、经历现实情境的问题研究,进一步培养学生的观察、比较、分析的能力。
(三)情感目标
1、通过对实际问题的分析,使学生进一步体会方程是刻画现实世界的有效数学模型,培养学生良好的数学应用意识。
2、培养合作交流和数学“化归”思想,体会二元一次方程的实际应用价值。
单击此处编辑母版副标题样式
单击此处编辑母版标题样式
生活中一切问题都可以转化为数学问题,
一切数学问题都可以转化为代数问题,
而一切代数问题又可以转化为方程,
因此,一旦解决了方程问题,
一切问题就将迎刃而解.
_____ 笛卡儿
两
数
差
为
7
两
数
和
为
9
不考虑牌的花色情况
§10.1
二元一次方程
x-1 +9y=0
请判断下列方程是否为二元一次方程,并说明理由。
(3)xy+2x+1=0
(1)2x+y+z=1
(2) x -5y=20
2
(4) +9y=0
x
1
含有两个未知数,并且含未知数的项的次数都是1的方程叫做二元一次方程.
为支持奥运, 年级组织了
〝猛男NBA〞比赛,我们
班在第一轮比赛中共得20
分. 比赛规定:赢一场得2
分,输一场得1分. 请问我们
班赢了多少场,输了多少场?
系
用
方
程
表
题
问
中
示
的
等
量
关
设:该队赢了x场,输了y场.
2x + y = 20
探究一:满足方程2x +y =20,且符合问题实际意义的x、y的 值有哪些?把它们填入下表.
y
X
适合二元一次方程的一对未知数的值叫做这个二元一次方程的一个解.
1
2
3
4
5
6
7
8
9
10
0
20
18
16
14
12
10
8
6
4
2
0
解:因为当x=2,y=18时,
例1、判断: x=2
y=18
是否是方程2x+y=20的解?
所以 不是方程2x+y=20的解
x=2 y=18
左边=2×2+1×18=22≠右边
探究二: 若不考虑实际背景,
二元一次方程2x+y=20,
有多少个解呢?
注意:一般地,一个二元一次方程的解不唯一,常常有无数个.
y=20 - 2x
再任意取x的值代入,
求出相应的y值
用含有一个未知数的代
数式表示另一个未知数
2x+y=20
原方程的解
注意:
1、也可用含
y的代数式
表示x……
2、前提是没
有实际背景
的限制
思考: 二元一次方程的解和一元一次方程的解有什么区别?
解的形式
解的个数
二元一次方程 的解
一元一次方程 的解
一个
无数个
一个未知数的
值 x=m
一对未知数的值
x=m
y=n
探究三:某球员在〝猛
男NBA〞的一场比赛中
共得35分, 其中罚球得10
分。请问他投中 了多少个
两分球?多少个三分球?
设:投中x个两分球,y个三分球.
则2x+3y=35-10
元
次
程
是
画
实
界
效
型
的
二
一
方
也
刻
现
世
有
模
即2x+3y=25
三分球y
两分球x
2x+3y=25
请你设计一张表格,列出
这名球员投中的两分球和
三分球的各种情况.
元
次
程
是
画
实
界
效
型
的
二
一
方
也
刻
现
世
有
模
11
1
8
3
5
2
5
7
根据所列表格回答:
(1)该球员最多投中了多少个三分球?
(2)该球员最多投中了多少个球?
7
5
3
1
三分球y
两分球x
11 8 5 2
根据所列表格回答:
(3)如果该球员投中了10个球,
那么其中几个两分球?几个三分球?
7
5
3
1
三分球y
两分球x
11 8 5 2
这节课你学到了什么?
课后反思
1、想想“用二元一次方程表达实际问题”与“用一元一次方程表达实际问题”有何异同?
2、用二元一次方程表达实际问题的关键是什么?
两
数
差
为
7
两
数
和
为
9
考虑牌的花色情况
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
