第2章相交线与平行线训练卷(Word版 含解析)
文档属性
| 名称 | 第2章相交线与平行线训练卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 282.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-28 11:39:59 | ||
图片预览



文档简介
第2章相交线与平行线训练卷
1.若∠α与∠β互补(∠α<∠β),则∠α与(∠β﹣∠α)的关系是( )
A.互补 B.互余 C.和为45° D.和为22.5°
2.下列说法中正确的个数为( )
①40°35′=24°55′;
②如果∠A+∠B=180°,那么∠A与∠B互为余角;
③经过两点有一条直线,并且只有一条直线;
④在同一平面内,不重合的两条直线不是平行就是相交.
A.1个 B.2个 C.3个 D.4个
3.将三角尺与直尺按如图所示摆放,下列关于∠α与∠β之间的关系一定正确的是( )
A.∠α=∠β B.∠α=∠β C.∠α+∠β=90° D.∠α+∠β=180°
4.如图,点E在CB的延长线上,下列条件中,能判定AB∥CD的是( )
A.∠1=∠4 B.∠2=∠3
C.∠A=∠ABE D.∠A+∠ABC=180°
5.如图,AB∥DE,那么∠BCD=( )
A.180°+∠1﹣∠2 B.∠1+∠2
C.∠2﹣∠1 D.180°+∠2﹣2∠1
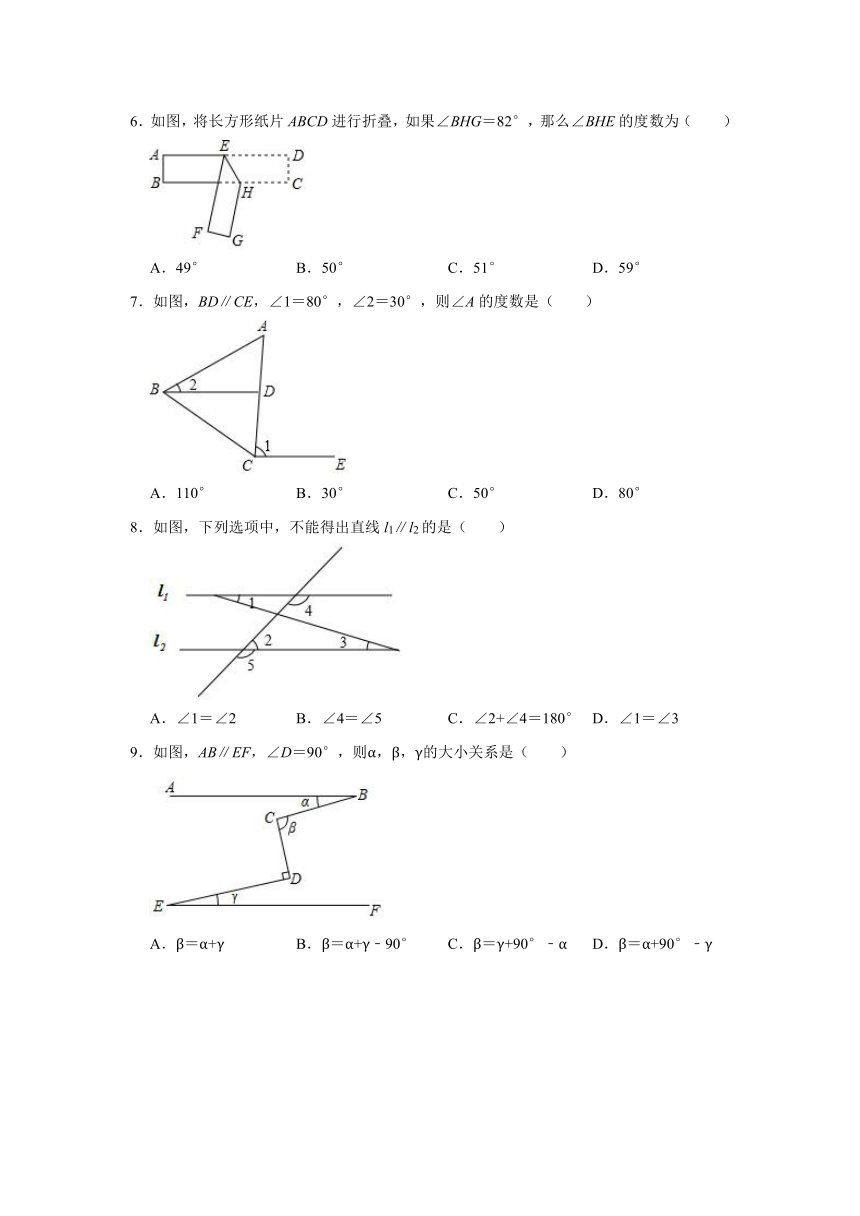
6.如图,将长方形纸片ABCD进行折叠,如果∠BHG=82°,那么∠BHE的度数为( )
A.49° B.50° C.51° D.59°
7.如图,BD∥CE,∠1=80°,∠2=30°,则∠A的度数是( )
A.110° B.30° C.50° D.80°
8.如图,下列选项中,不能得出直线l1∥l2的是( )
A.∠1=∠2 B.∠4=∠5 C.∠2+∠4=180° D.∠1=∠3
9.如图,AB∥EF,∠D=90°,则α,β,γ的大小关系是( )
A.β=α+γ B.β=α+γ﹣90° C.β=γ+90°﹣α D.β=α+90°﹣γ
10.如图,已知CB∥DF,则下列结论成立的是( )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠3 D.∠1+∠2=180°
11.在同一平面内的三条直线,它们的交点个数是 .
12.已知∠1与∠2互余,∠2与∠3互补,若∠1=33°27',则∠3= .
13.如图,直线AB、CD相交于点O,∠COE是直角,OF平分∠AOD,若∠BOE=42°,则∠AOF的度数是 .
14.在直线AB上任取一点O,过点O作射线OC,OD,使∠COD=90°,当∠AOC=50°时,∠BOD的度数是 .
15.如图,直线AB与CD相交于点O,射线OM是∠AOC的平分线,如果∠MOC=25°,那么∠BOC= .
16.如图,已知a∥b,∠1=50°,∠2=115°,则∠3= .
17.将一把直尺和一块含30°角的三角板ABC按如图所示的位置放置,如果∠CDE=42°,那么∠BAF的度数为 .
18.如图,如果AB∥CD,则角α=130°,γ=20°,则β= .
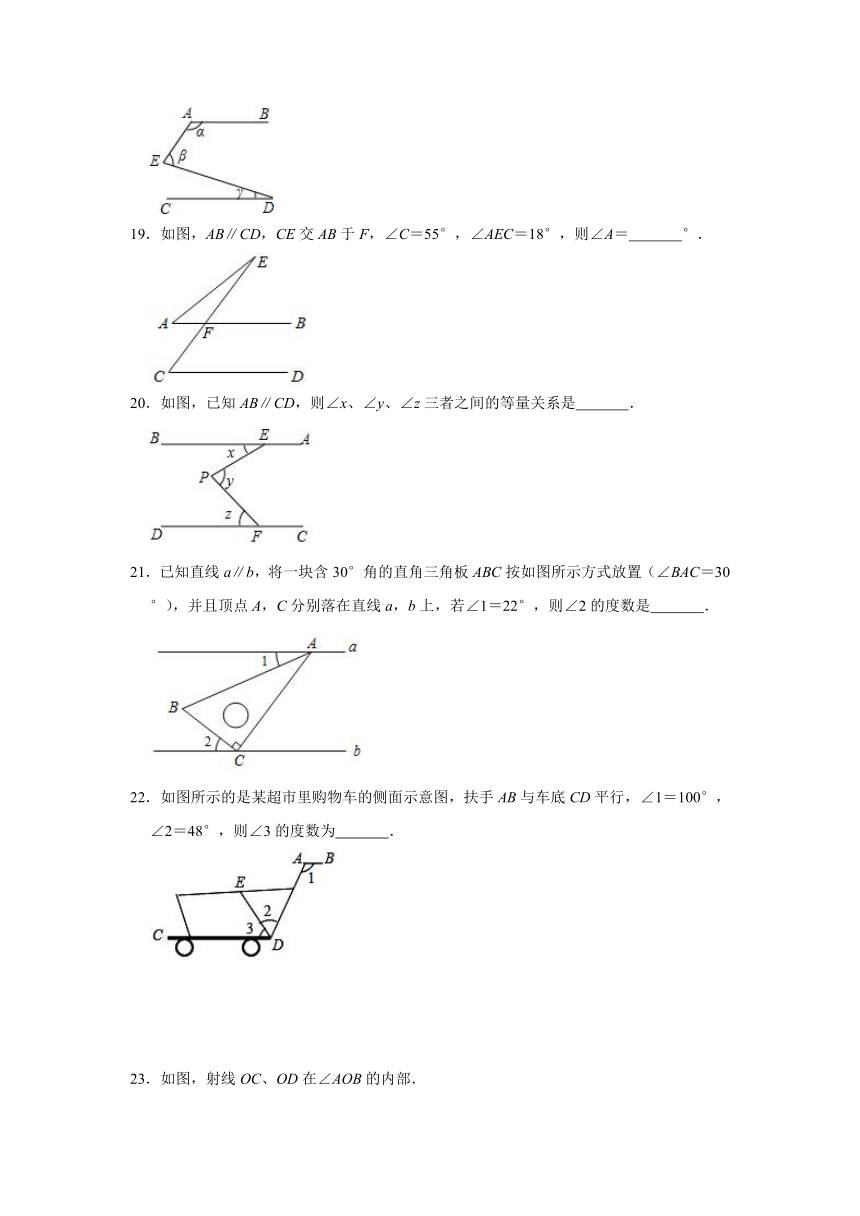
19.如图,AB∥CD,CE交AB于F,∠C=55°,∠AEC=18°,则∠A= °.
20.如图,已知AB∥CD,则∠x、∠y、∠z三者之间的等量关系是 .
21.已知直线a∥b,将一块含30°角的直角三角板ABC按如图所示方式放置(∠BAC=30°),并且顶点A,C分别落在直线a,b上,若∠1=22°,则∠2的度数是 .
22.如图所示的是某超市里购物车的侧面示意图,扶手AB与车底CD平行,∠1=100°,∠2=48°,则∠3的度数为 .
23.如图,射线OC、OD在∠AOB的内部.
(1)∠AOB=169°,∠AOC=∠BOD=90°,求∠COD的度数.
(2)当∠AOC=∠BOD=90°,试判断∠AOD与∠BOC的关系,说明理由.
(3)当∠AOC=∠BOD=α,(2)中的结论还存在吗?为什么?
24.如图①,直线l1∥l2,直线EF和直线l1、l2分别交于C、D两点,点A、B分别在直线l1、l2上,点P在直线EF上,连接PA、PB.
猜想:如图①,若点P在线段CD上,∠PAC=15°,∠PBD=40°,则∠APB的大小为 度.
探究:如图①,若点P在线段CD上,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
拓展:如图②,若点P在射线CE上或在射线DF上时,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
25.如图,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D.
求证:AC∥DF.
26.同一平面内的两条直线有相交和平行两种位置关系.
(1)如图1,若AB∥CD,点P在AB、CD内部,请写出∠BPD、∠B、∠D之间的数量关系(不必说明理由);
(2)如图2,将直线AB绕点B逆时针方向转一定角度交直线CD于点Q,利用(1)中的结论求∠BPD、∠B、∠D、∠BQD之间有何数量关系?并证明你的结论;
(3)如图3,设BF交AC于点M,AE交DF于点N.已知∠AMB=140°,∠ANF=105°,利用(2)中的结论直接写出∠B+∠E+∠F的度数和∠A比∠F大多少度.
27.直线AB∥CD,E为直线AB、CD之间的一点,完成以下问题:
(1)如图1,若∠B=15°,∠BED=90°,则∠D= ;
(2)如图2,若∠B=α,∠D=β,求出∠BED的度数(用a、β表示);
(3)如图3,若∠B=α,∠C=β,则a、β与∠BEC之间有什么等量关系?请猜想证明.
28.已知一个角的两边与另一个角的两边分别平行,结合图,试探索这两个角之间的关系,并说明你的结论.
(1)如图1,AB∥EF,BC∥DE,∠1与∠2有何关系?说明理由;
(2)如图2,AB∥EF,BC∥DE,∠1与∠2有何关系?说明理由;
(3)由(1)(2)你能得出的结论是:如果 ,那么 ;
(4)若两个角的两边分别平行,且一个角比另一个角的2倍少60°,则这两个角度数的分别是 .
29.已知AB∥CD,点E在AB与CD之间.
(1)图1中,试说明:∠BED=∠ABE+∠CDE;
(2)图2中,∠ABE的平分线与∠CDE的平分线相交于点F,请利用(1)的结论说明:∠BED=2∠BFD.
(3)图3中,∠ABE的平分线与∠CDE的平分线相交于点F,请直接写出∠BED与∠BFD之间的数量关系.
参考答案
1.解:因为∠α与∠β互补(∠α<∠β),
所以∠α+∠β=180°,
所以∠α+(∠β﹣∠α)=,
所以∠α与(∠β﹣∠α)的关系是互余.
故选:B.
2.解:①40°35′=40×60′+35′=24°35′,①错误;
②两个角的和等于180度,这两个角互为补角,②错误;
③直线的性质,③正确;
④在同一平面内,两条不重合直线的位置关系有相交和平行两种,④正确.
故选:B.
3.解:∠α+∠β=180°﹣90°=90°,
故选:C.
4.解:A.由∠1=∠4,不能判定AB∥CD,故本选项错误;
B.由∠2=∠3,能判定AB∥CD,故本选项正确;
C.由∠A=∠ABE,不能判定AB∥CD,故本选项错误;
D.由∠A+∠ABC=180°,不能判定AB∥CD,故本选项错误.
故选:B.
5.解:过点C作CF∥AB,如图:
∵AB∥DE,
∴AB∥DE∥CF,
∴∠BCF=∠1①,∠2+∠DCF=180°②,
∴①+②得,∠BCF+∠DCF+∠2=∠1+180°,即∠BCD=180°+∠1﹣∠2.
故选:A.
6.解:∵四边形ABCD是长方形,
∴AD∥BC,
∴∠DEH=∠BHE,∠DEH+∠EHC=180°,
根据折叠可知:
∠CHE=∠EHG,
∵∠EHC=∠BHE+∠BHG,
∴∠BHE+∠BHE+∠BHG=180°,
∴2∠BHE=180°﹣82°=98°,
∴∠BHE=49°.
故选:A.
7.解:∵BD∥CE,∠1=80°,
∴∠BDC=∠1=80°,
又∵∠BDC=∠2+∠A,∠2=30°,
∴∠A=80°﹣30°=50°.
故选:C.
8.解:A、∠1=∠2,不能判断直线l1∥l2,故此选项符合题意;
B、根据同位角相等,两直线平行,可判断直线l1∥l2,故此选项不合题意;
C、根据同旁内角互补,两直线平行,可判断直线l1∥l2,故此选项不合题意;
D、根据内错角相等,两直线平行,可判断直线l1∥l2,故此选项不合题意.
故选:A.
9.解:如图,过点C和点D作CG∥AB,DH∥AB,
∴CG∥DH∥AB,
∵AB∥EF,
∴AB∥EF∥CG∥DH,
∵CG∥AB,
∴∠BCG=α,
∴∠GCD=∠BCD﹣∠BCG=β﹣α,
∵CG∥DH,
∴∠CDH=∠GCD=β﹣α,
∵HD∥EF,
∴∠HDE=γ,
∵∠EDC=∠HDE+∠CDH=90°,
∴γ+β﹣α=90°,
∴β=α+90°﹣γ.
故选:D.
10.解:∵CB∥DF,
∴∠2=∠3(两条直线平行,同位角相等).
故选:B.
11.解:当三条直线互相平行,交点是个0;
当两条直线平行,与第三条直线相交,交点是2个;
当三条直线两两相交交于同一点,交点个数是1个;
当三条直线两两相交且不交于同一点,交点个数是3个;
故答案为:0个或1个或2个或3个.
12.解:∵∠1与∠2互余,
∴∠2=90°﹣∠1,
∵∠2与∠3互补,
∴∠3=180°﹣∠2=180°﹣(90°﹣∠1)=90°+∠1,
∵∠1=33°27',
∴∠3=123°27',
故答案为:123°27'.
13.解:∵∠COE是直角,
∴∠COE=90°,
∴∠DOE=180°﹣90°=90°,
∵∠BOE=42°,
∴∠BOD=∠DOE﹣∠BOE=90°﹣42°=48°,
∴∠AOD=180°﹣∠BOD=180°﹣48°=132°,
∵OF平分∠AOD,
∠AOF=∠AOD=×132°=66°.
故答案为:66°.
14.解:如图,射线OC、OD在直线AB的同一侧时,
∵∠COD=90°,
∴∠BOD=180°﹣90°﹣∠AOC=180°﹣90°﹣50°=40°,
射线OC、OD在直线AB的两侧时,
∵∠COD=90°,
∴∠AOD=90°﹣∠AOC=90°﹣50°=40°,
∴∠BOD=180°﹣∠AOD=180°﹣40°=140°.
综上所述,∠BOD的度数是40°或140°.
故答案为:40°或140°.
15.解:∵射线OM是∠AOC的平分线,∠MOC=25°,
∴∠AOC=2∠MOC=50°,
又∵∠AOB是平角,
∴∠BOC=180°﹣∠AOC=130°,
故答案为:130°.
16.解:如图:
∵a∥b,∠1=50°,
∴∠4=∠1=50°,
∵∠2=115°,∠2=∠3+∠4,
∴∠3=∠2﹣∠4=115°﹣50°=65°.
故答案为:65°.
17.解:由题意知DE∥AF,∠CDE=42°,
∴∠AFD=∠CDE=42°,
∵∠B=30°,
∴∠BAF=∠AFD﹣∠B=42°﹣30°=12°,
故答案为:12°.
18.解:如图,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠A+∠AEF=180°,∠D=∠FED,
∴∠AEF=180°﹣130°=50°,∠FED=20°,
∴∠AED=∠AEF+∠FED=50°+20°=70°.
即β=70°.
故答案为:70°.
19.解:∵AB∥CD,∠C=55°,
∴∠EFB=∠C=55°,
∴∠AFE=180°﹣∠EFB=125°,
∵∠AEC=18°,
∴∠A=180°﹣∠AFE﹣∠AEC=37°,
故答案为:37.
20.解:如图,过点P作PG∥AB,
∴∠EPG=∠x,
∵AB∥CD,
∴PG∥CD,
∴∠FPG=∠z,
∴∠EPF=∠EPG+∠FPG=∠x+∠z.
∴∠x+∠z=∠y.
故答案为:∠x+∠z=∠y.
21.解:如图,过点B作BD∥a,
∴∠ABD=∠1=22°,
∵a∥b,
∴BD∥b,
∴∠2=∠DBC=∠ABC﹣∠ABD=60°﹣22°=38°.
故答案为:38°.
22.解:∵AB∥CD,
∴∠1=∠CDA=100°,
∵∠2=48°,
∴∠3=52°.
故答案为:52°.
23.解:(1)因为∠AOB=169°,∠AOC=∠BOD=90°,
所以∠BOC=∠AOB﹣∠AOC=169°﹣90°=79°,
所以∠COD=∠BOD﹣∠BOC=90°﹣79°=11°;
(2)∠AOD=∠BOC,理由:
因为∠AOC=∠BOD=90°,
所以∠AOD+∠DOC=90°,∠BOC+∠DOC=90°
所以∠AOD=∠BOC.
(3)存在,仍然有∠AOD=∠BOC.理由:
因为∠AOD=∠AOC﹣∠DOC,∠BOC=∠BOD﹣∠DOC.
又因为∠AOC=∠BOD=α,
所以∠AOD=∠BOC.
24.解:猜想:如图①,过点P作PG∥l1,
∵l1∥l2,
∴l1∥l2∥PG,
∴∠APG=∠PAC=15°,∠BPG=∠PBD=40°,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD=15°+40°=55°,
∴∠APB的大小为55度,
故答案为:55;
探究:如图①,∠PAC=∠APB﹣∠PBD,理由如下:
∵l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD,
∴∠PAC=∠APB﹣∠PBD;
拓展:∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD,理由如下:
如图,当点P在射线CE上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠BPG﹣∠APB,
∴∠PAC=∠PBD﹣∠APB;
当点P在射线DF上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠APB+∠BPG,
∴∠PAC=∠APB+∠PBD,
综上所述:当点P在射线CE上或在射线DF上时,∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD.
25.证明:∵∠2=∠3,∠1=∠2,
∴∠1=∠3,
∴BD∥CE,
∴∠C=∠ABD;
又∵∠C=∠D,
∴∠D=∠ABD,
∴AC∥DF.
26.解:(1)过点P作PE∥AB,
∵AB∥CD,
∴AB∥EP∥CD,
∴∠B=∠1,∠D=∠2,
∴∠BPD=∠B+∠D;
(2)如图2,连接QP并延长,
结论:∠BPD=∠BQD+∠B+∠D.
∠BPD=(∠BQP+∠B)+(∠DQP+∠D)=∠BQD+∠B+∠D;
(3)∵∠ANF=105°,
∴∠ENF=∠B+∠E+∠F=180°﹣105°=75°,
∵∠A=∠AMB﹣∠B﹣∠E,
∠F=180°﹣∠ANF﹣∠B﹣∠E,
∴∠A﹣∠F=∠AMB+∠ANF﹣180°=65°.
答:∠B+∠E+∠F的度数为:75°;
∠A比∠F大65°.
27.解:(1)过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∵∠B=15°,
∴∠BEF=15°,
又∵∠BED=90°,
∴∠DEF=75°,
∵EF∥CD,
∴∠D=75°,
故答案为:75°;
(2)过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠B+∠BEF+∠DEF+∠D=360°,
又∵∠B=α,∠D=β,
∴∠BED=∠BEF+∠DEF=360°﹣α﹣β,
故答案为:∠BED=360°﹣α﹣β;
(3)猜想:∠BEC=180°﹣α+β.
证明:过点E作EF∥AB,
则∠BEF=180°﹣∠B=180°﹣α,
∵AB∥EF,AB∥CD,
∴EF∥CD,
∴∠CEF=∠C=β,
∴∠BEC=∠BEF+∠CEF=180°﹣α+β.
28.解:(1)∠1=∠2,
理由:如图1,
∵AB∥EF,
∴∠3=∠2,
∵BC∥DE,
∴∠3=∠1,
∴∠1=∠2;
(2)∠1+∠2=180°,
理由:如图2,
∵AB∥EF,
∴∠3+∠2=180°,
∵BC∥DE,
∴∠3=∠1,
∴∠1+∠2=180°.
(3)如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
故答案为:一个角的两边与另一个角的两边分别平行,这两个角相等或互补;
(4)设另一个角为x°,根据以上结论得:
2x﹣60=x或2x﹣60+x=180,
解得:x=60,或x=80,
故答案为:60°、60°或80°,100°.
29.解:(1)如图1中,过点E作EG∥AB,
则∠BEG=∠ABE,
因为AB∥CD,EG∥AB,
所以CD∥EG,
所以∠DEG=∠CDE,
所以∠BEG+∠DEG=∠ABE+∠CDE,
即∠BED=∠ABE+∠CDE;
(2)图2中,因为BF平分∠ABE,
所以∠ABE=2∠ABF,
因为DF平分∠CDE,
所以∠CDE=2∠CDF,
所以∠ABE+∠CDE=2∠ABF+2∠CDF=2(∠ABF+∠CDF),
由(1)得:因为AB∥CD,
所以∠BED=∠ABE+∠CDE,
∠BFD=∠ABF+∠CDF,
所以∠BED=2∠BFD.
(3)∠BED=360°﹣2∠BFD.
图3中,过点E作EG∥AB,
则∠BEG+∠ABE=180°,
因为AB∥CD,EG∥AB,
所以CD∥EG,
所以∠DEG+∠CDE=180°,
所以∠BEG+∠DEG=360°﹣(∠ABE+∠CDE),
即∠BED=360°﹣(∠ABE+∠CDE),
因为BF平分∠ABE,
所以∠ABE=2∠ABF,
因为DF平分∠CDE,
所以∠CDE=2∠CDF,
∠BED=360°﹣2(∠ABF+∠CDF),
由(1)得:因为AB∥CD,
所以∠BFD=∠ABF+∠CDF,
所以∠BED=360°﹣2∠BFD
1.若∠α与∠β互补(∠α<∠β),则∠α与(∠β﹣∠α)的关系是( )
A.互补 B.互余 C.和为45° D.和为22.5°
2.下列说法中正确的个数为( )
①40°35′=24°55′;
②如果∠A+∠B=180°,那么∠A与∠B互为余角;
③经过两点有一条直线,并且只有一条直线;
④在同一平面内,不重合的两条直线不是平行就是相交.
A.1个 B.2个 C.3个 D.4个
3.将三角尺与直尺按如图所示摆放,下列关于∠α与∠β之间的关系一定正确的是( )
A.∠α=∠β B.∠α=∠β C.∠α+∠β=90° D.∠α+∠β=180°
4.如图,点E在CB的延长线上,下列条件中,能判定AB∥CD的是( )
A.∠1=∠4 B.∠2=∠3
C.∠A=∠ABE D.∠A+∠ABC=180°
5.如图,AB∥DE,那么∠BCD=( )
A.180°+∠1﹣∠2 B.∠1+∠2
C.∠2﹣∠1 D.180°+∠2﹣2∠1
6.如图,将长方形纸片ABCD进行折叠,如果∠BHG=82°,那么∠BHE的度数为( )
A.49° B.50° C.51° D.59°
7.如图,BD∥CE,∠1=80°,∠2=30°,则∠A的度数是( )
A.110° B.30° C.50° D.80°
8.如图,下列选项中,不能得出直线l1∥l2的是( )
A.∠1=∠2 B.∠4=∠5 C.∠2+∠4=180° D.∠1=∠3
9.如图,AB∥EF,∠D=90°,则α,β,γ的大小关系是( )
A.β=α+γ B.β=α+γ﹣90° C.β=γ+90°﹣α D.β=α+90°﹣γ
10.如图,已知CB∥DF,则下列结论成立的是( )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠3 D.∠1+∠2=180°
11.在同一平面内的三条直线,它们的交点个数是 .
12.已知∠1与∠2互余,∠2与∠3互补,若∠1=33°27',则∠3= .
13.如图,直线AB、CD相交于点O,∠COE是直角,OF平分∠AOD,若∠BOE=42°,则∠AOF的度数是 .
14.在直线AB上任取一点O,过点O作射线OC,OD,使∠COD=90°,当∠AOC=50°时,∠BOD的度数是 .
15.如图,直线AB与CD相交于点O,射线OM是∠AOC的平分线,如果∠MOC=25°,那么∠BOC= .
16.如图,已知a∥b,∠1=50°,∠2=115°,则∠3= .
17.将一把直尺和一块含30°角的三角板ABC按如图所示的位置放置,如果∠CDE=42°,那么∠BAF的度数为 .
18.如图,如果AB∥CD,则角α=130°,γ=20°,则β= .
19.如图,AB∥CD,CE交AB于F,∠C=55°,∠AEC=18°,则∠A= °.
20.如图,已知AB∥CD,则∠x、∠y、∠z三者之间的等量关系是 .
21.已知直线a∥b,将一块含30°角的直角三角板ABC按如图所示方式放置(∠BAC=30°),并且顶点A,C分别落在直线a,b上,若∠1=22°,则∠2的度数是 .
22.如图所示的是某超市里购物车的侧面示意图,扶手AB与车底CD平行,∠1=100°,∠2=48°,则∠3的度数为 .
23.如图,射线OC、OD在∠AOB的内部.
(1)∠AOB=169°,∠AOC=∠BOD=90°,求∠COD的度数.
(2)当∠AOC=∠BOD=90°,试判断∠AOD与∠BOC的关系,说明理由.
(3)当∠AOC=∠BOD=α,(2)中的结论还存在吗?为什么?
24.如图①,直线l1∥l2,直线EF和直线l1、l2分别交于C、D两点,点A、B分别在直线l1、l2上,点P在直线EF上,连接PA、PB.
猜想:如图①,若点P在线段CD上,∠PAC=15°,∠PBD=40°,则∠APB的大小为 度.
探究:如图①,若点P在线段CD上,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
拓展:如图②,若点P在射线CE上或在射线DF上时,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
25.如图,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D.
求证:AC∥DF.
26.同一平面内的两条直线有相交和平行两种位置关系.
(1)如图1,若AB∥CD,点P在AB、CD内部,请写出∠BPD、∠B、∠D之间的数量关系(不必说明理由);
(2)如图2,将直线AB绕点B逆时针方向转一定角度交直线CD于点Q,利用(1)中的结论求∠BPD、∠B、∠D、∠BQD之间有何数量关系?并证明你的结论;
(3)如图3,设BF交AC于点M,AE交DF于点N.已知∠AMB=140°,∠ANF=105°,利用(2)中的结论直接写出∠B+∠E+∠F的度数和∠A比∠F大多少度.
27.直线AB∥CD,E为直线AB、CD之间的一点,完成以下问题:
(1)如图1,若∠B=15°,∠BED=90°,则∠D= ;
(2)如图2,若∠B=α,∠D=β,求出∠BED的度数(用a、β表示);
(3)如图3,若∠B=α,∠C=β,则a、β与∠BEC之间有什么等量关系?请猜想证明.
28.已知一个角的两边与另一个角的两边分别平行,结合图,试探索这两个角之间的关系,并说明你的结论.
(1)如图1,AB∥EF,BC∥DE,∠1与∠2有何关系?说明理由;
(2)如图2,AB∥EF,BC∥DE,∠1与∠2有何关系?说明理由;
(3)由(1)(2)你能得出的结论是:如果 ,那么 ;
(4)若两个角的两边分别平行,且一个角比另一个角的2倍少60°,则这两个角度数的分别是 .
29.已知AB∥CD,点E在AB与CD之间.
(1)图1中,试说明:∠BED=∠ABE+∠CDE;
(2)图2中,∠ABE的平分线与∠CDE的平分线相交于点F,请利用(1)的结论说明:∠BED=2∠BFD.
(3)图3中,∠ABE的平分线与∠CDE的平分线相交于点F,请直接写出∠BED与∠BFD之间的数量关系.
参考答案
1.解:因为∠α与∠β互补(∠α<∠β),
所以∠α+∠β=180°,
所以∠α+(∠β﹣∠α)=,
所以∠α与(∠β﹣∠α)的关系是互余.
故选:B.
2.解:①40°35′=40×60′+35′=24°35′,①错误;
②两个角的和等于180度,这两个角互为补角,②错误;
③直线的性质,③正确;
④在同一平面内,两条不重合直线的位置关系有相交和平行两种,④正确.
故选:B.
3.解:∠α+∠β=180°﹣90°=90°,
故选:C.
4.解:A.由∠1=∠4,不能判定AB∥CD,故本选项错误;
B.由∠2=∠3,能判定AB∥CD,故本选项正确;
C.由∠A=∠ABE,不能判定AB∥CD,故本选项错误;
D.由∠A+∠ABC=180°,不能判定AB∥CD,故本选项错误.
故选:B.
5.解:过点C作CF∥AB,如图:
∵AB∥DE,
∴AB∥DE∥CF,
∴∠BCF=∠1①,∠2+∠DCF=180°②,
∴①+②得,∠BCF+∠DCF+∠2=∠1+180°,即∠BCD=180°+∠1﹣∠2.
故选:A.
6.解:∵四边形ABCD是长方形,
∴AD∥BC,
∴∠DEH=∠BHE,∠DEH+∠EHC=180°,
根据折叠可知:
∠CHE=∠EHG,
∵∠EHC=∠BHE+∠BHG,
∴∠BHE+∠BHE+∠BHG=180°,
∴2∠BHE=180°﹣82°=98°,
∴∠BHE=49°.
故选:A.
7.解:∵BD∥CE,∠1=80°,
∴∠BDC=∠1=80°,
又∵∠BDC=∠2+∠A,∠2=30°,
∴∠A=80°﹣30°=50°.
故选:C.
8.解:A、∠1=∠2,不能判断直线l1∥l2,故此选项符合题意;
B、根据同位角相等,两直线平行,可判断直线l1∥l2,故此选项不合题意;
C、根据同旁内角互补,两直线平行,可判断直线l1∥l2,故此选项不合题意;
D、根据内错角相等,两直线平行,可判断直线l1∥l2,故此选项不合题意.
故选:A.
9.解:如图,过点C和点D作CG∥AB,DH∥AB,
∴CG∥DH∥AB,
∵AB∥EF,
∴AB∥EF∥CG∥DH,
∵CG∥AB,
∴∠BCG=α,
∴∠GCD=∠BCD﹣∠BCG=β﹣α,
∵CG∥DH,
∴∠CDH=∠GCD=β﹣α,
∵HD∥EF,
∴∠HDE=γ,
∵∠EDC=∠HDE+∠CDH=90°,
∴γ+β﹣α=90°,
∴β=α+90°﹣γ.
故选:D.
10.解:∵CB∥DF,
∴∠2=∠3(两条直线平行,同位角相等).
故选:B.
11.解:当三条直线互相平行,交点是个0;
当两条直线平行,与第三条直线相交,交点是2个;
当三条直线两两相交交于同一点,交点个数是1个;
当三条直线两两相交且不交于同一点,交点个数是3个;
故答案为:0个或1个或2个或3个.
12.解:∵∠1与∠2互余,
∴∠2=90°﹣∠1,
∵∠2与∠3互补,
∴∠3=180°﹣∠2=180°﹣(90°﹣∠1)=90°+∠1,
∵∠1=33°27',
∴∠3=123°27',
故答案为:123°27'.
13.解:∵∠COE是直角,
∴∠COE=90°,
∴∠DOE=180°﹣90°=90°,
∵∠BOE=42°,
∴∠BOD=∠DOE﹣∠BOE=90°﹣42°=48°,
∴∠AOD=180°﹣∠BOD=180°﹣48°=132°,
∵OF平分∠AOD,
∠AOF=∠AOD=×132°=66°.
故答案为:66°.
14.解:如图,射线OC、OD在直线AB的同一侧时,
∵∠COD=90°,
∴∠BOD=180°﹣90°﹣∠AOC=180°﹣90°﹣50°=40°,
射线OC、OD在直线AB的两侧时,
∵∠COD=90°,
∴∠AOD=90°﹣∠AOC=90°﹣50°=40°,
∴∠BOD=180°﹣∠AOD=180°﹣40°=140°.
综上所述,∠BOD的度数是40°或140°.
故答案为:40°或140°.
15.解:∵射线OM是∠AOC的平分线,∠MOC=25°,
∴∠AOC=2∠MOC=50°,
又∵∠AOB是平角,
∴∠BOC=180°﹣∠AOC=130°,
故答案为:130°.
16.解:如图:
∵a∥b,∠1=50°,
∴∠4=∠1=50°,
∵∠2=115°,∠2=∠3+∠4,
∴∠3=∠2﹣∠4=115°﹣50°=65°.
故答案为:65°.
17.解:由题意知DE∥AF,∠CDE=42°,
∴∠AFD=∠CDE=42°,
∵∠B=30°,
∴∠BAF=∠AFD﹣∠B=42°﹣30°=12°,
故答案为:12°.
18.解:如图,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠A+∠AEF=180°,∠D=∠FED,
∴∠AEF=180°﹣130°=50°,∠FED=20°,
∴∠AED=∠AEF+∠FED=50°+20°=70°.
即β=70°.
故答案为:70°.
19.解:∵AB∥CD,∠C=55°,
∴∠EFB=∠C=55°,
∴∠AFE=180°﹣∠EFB=125°,
∵∠AEC=18°,
∴∠A=180°﹣∠AFE﹣∠AEC=37°,
故答案为:37.
20.解:如图,过点P作PG∥AB,
∴∠EPG=∠x,
∵AB∥CD,
∴PG∥CD,
∴∠FPG=∠z,
∴∠EPF=∠EPG+∠FPG=∠x+∠z.
∴∠x+∠z=∠y.
故答案为:∠x+∠z=∠y.
21.解:如图,过点B作BD∥a,
∴∠ABD=∠1=22°,
∵a∥b,
∴BD∥b,
∴∠2=∠DBC=∠ABC﹣∠ABD=60°﹣22°=38°.
故答案为:38°.
22.解:∵AB∥CD,
∴∠1=∠CDA=100°,
∵∠2=48°,
∴∠3=52°.
故答案为:52°.
23.解:(1)因为∠AOB=169°,∠AOC=∠BOD=90°,
所以∠BOC=∠AOB﹣∠AOC=169°﹣90°=79°,
所以∠COD=∠BOD﹣∠BOC=90°﹣79°=11°;
(2)∠AOD=∠BOC,理由:
因为∠AOC=∠BOD=90°,
所以∠AOD+∠DOC=90°,∠BOC+∠DOC=90°
所以∠AOD=∠BOC.
(3)存在,仍然有∠AOD=∠BOC.理由:
因为∠AOD=∠AOC﹣∠DOC,∠BOC=∠BOD﹣∠DOC.
又因为∠AOC=∠BOD=α,
所以∠AOD=∠BOC.
24.解:猜想:如图①,过点P作PG∥l1,
∵l1∥l2,
∴l1∥l2∥PG,
∴∠APG=∠PAC=15°,∠BPG=∠PBD=40°,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD=15°+40°=55°,
∴∠APB的大小为55度,
故答案为:55;
探究:如图①,∠PAC=∠APB﹣∠PBD,理由如下:
∵l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD,
∴∠PAC=∠APB﹣∠PBD;
拓展:∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD,理由如下:
如图,当点P在射线CE上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠BPG﹣∠APB,
∴∠PAC=∠PBD﹣∠APB;
当点P在射线DF上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠APB+∠BPG,
∴∠PAC=∠APB+∠PBD,
综上所述:当点P在射线CE上或在射线DF上时,∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD.
25.证明:∵∠2=∠3,∠1=∠2,
∴∠1=∠3,
∴BD∥CE,
∴∠C=∠ABD;
又∵∠C=∠D,
∴∠D=∠ABD,
∴AC∥DF.
26.解:(1)过点P作PE∥AB,
∵AB∥CD,
∴AB∥EP∥CD,
∴∠B=∠1,∠D=∠2,
∴∠BPD=∠B+∠D;
(2)如图2,连接QP并延长,
结论:∠BPD=∠BQD+∠B+∠D.
∠BPD=(∠BQP+∠B)+(∠DQP+∠D)=∠BQD+∠B+∠D;
(3)∵∠ANF=105°,
∴∠ENF=∠B+∠E+∠F=180°﹣105°=75°,
∵∠A=∠AMB﹣∠B﹣∠E,
∠F=180°﹣∠ANF﹣∠B﹣∠E,
∴∠A﹣∠F=∠AMB+∠ANF﹣180°=65°.
答:∠B+∠E+∠F的度数为:75°;
∠A比∠F大65°.
27.解:(1)过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∵∠B=15°,
∴∠BEF=15°,
又∵∠BED=90°,
∴∠DEF=75°,
∵EF∥CD,
∴∠D=75°,
故答案为:75°;
(2)过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠B+∠BEF+∠DEF+∠D=360°,
又∵∠B=α,∠D=β,
∴∠BED=∠BEF+∠DEF=360°﹣α﹣β,
故答案为:∠BED=360°﹣α﹣β;
(3)猜想:∠BEC=180°﹣α+β.
证明:过点E作EF∥AB,
则∠BEF=180°﹣∠B=180°﹣α,
∵AB∥EF,AB∥CD,
∴EF∥CD,
∴∠CEF=∠C=β,
∴∠BEC=∠BEF+∠CEF=180°﹣α+β.
28.解:(1)∠1=∠2,
理由:如图1,
∵AB∥EF,
∴∠3=∠2,
∵BC∥DE,
∴∠3=∠1,
∴∠1=∠2;
(2)∠1+∠2=180°,
理由:如图2,
∵AB∥EF,
∴∠3+∠2=180°,
∵BC∥DE,
∴∠3=∠1,
∴∠1+∠2=180°.
(3)如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
故答案为:一个角的两边与另一个角的两边分别平行,这两个角相等或互补;
(4)设另一个角为x°,根据以上结论得:
2x﹣60=x或2x﹣60+x=180,
解得:x=60,或x=80,
故答案为:60°、60°或80°,100°.
29.解:(1)如图1中,过点E作EG∥AB,
则∠BEG=∠ABE,
因为AB∥CD,EG∥AB,
所以CD∥EG,
所以∠DEG=∠CDE,
所以∠BEG+∠DEG=∠ABE+∠CDE,
即∠BED=∠ABE+∠CDE;
(2)图2中,因为BF平分∠ABE,
所以∠ABE=2∠ABF,
因为DF平分∠CDE,
所以∠CDE=2∠CDF,
所以∠ABE+∠CDE=2∠ABF+2∠CDF=2(∠ABF+∠CDF),
由(1)得:因为AB∥CD,
所以∠BED=∠ABE+∠CDE,
∠BFD=∠ABF+∠CDF,
所以∠BED=2∠BFD.
(3)∠BED=360°﹣2∠BFD.
图3中,过点E作EG∥AB,
则∠BEG+∠ABE=180°,
因为AB∥CD,EG∥AB,
所以CD∥EG,
所以∠DEG+∠CDE=180°,
所以∠BEG+∠DEG=360°﹣(∠ABE+∠CDE),
即∠BED=360°﹣(∠ABE+∠CDE),
因为BF平分∠ABE,
所以∠ABE=2∠ABF,
因为DF平分∠CDE,
所以∠CDE=2∠CDF,
∠BED=360°﹣2(∠ABF+∠CDF),
由(1)得:因为AB∥CD,
所以∠BFD=∠ABF+∠CDF,
所以∠BED=360°﹣2∠BFD
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
