人教版八年级下册第18章《平行四边形》单元练习题(Word版 含解析)
文档属性
| 名称 | 人教版八年级下册第18章《平行四边形》单元练习题(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 138.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-28 20:05:46 | ||
图片预览


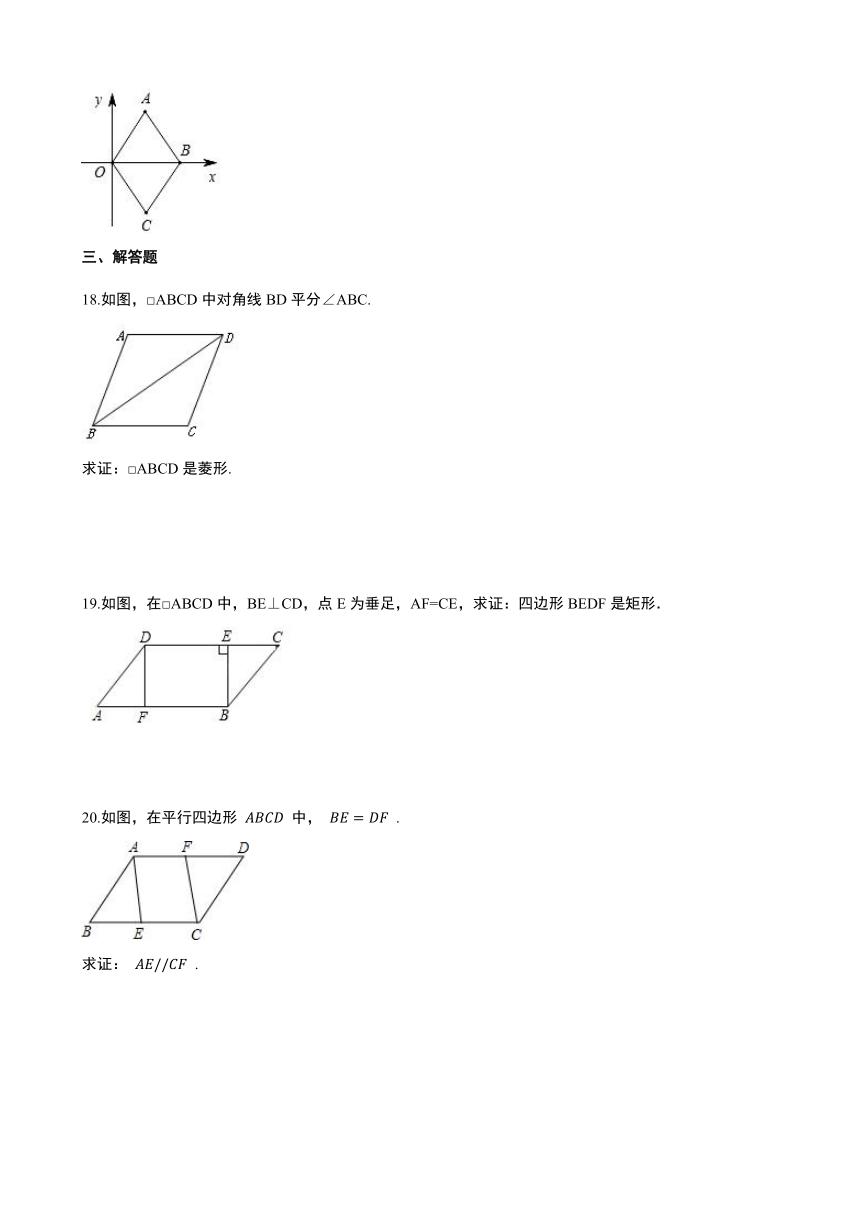
文档简介
人教版八年级下册第18章《平行四边形》单元练习题
一、选择题
1.在平行四边形 ABCD 中,若 ∠A=2∠B ,则 ∠D 的度数是(? )
A.?50°???????????????????????????????????????B.?60°???????????????????????????????????????C.?70°???????????????????????????????????????D.?80°
2.平行四边形、矩形、菱形、正方形共有的性质是(?? ).
A.?对角线互相平分?????????????B.?对角线相等?????????????C.?对角线互相垂直?????????????D.?对角形互相垂直平分
3.矩形具有而菱形不具有的性质是(?? )
A.?对角相等???????????????????????B.?对角线互相垂直???????????????????????C.?对角线相等???????????????????????D.?对边平行
4.小军不慎将一块平行四边形玻璃打碎成如图所示的四块,他带了两块碎玻璃到商店配成一块与原来相同的平行四边形玻璃,他带的碎玻璃编号是(?? )
A.?①②?????????????????????????????????????B.?①④?????????????????????????????????????C.?②③?????????????????????????????????????D.?②④
5.已知四边形ABCD是平行四边形,则下列结论中正确的是(?? )
A.?当AB⊥BD时,它是菱形 B.?当AC=BD时,它是正方形
C.?当∠ABC=90°时,它是矩形 D.?当AB=BC时,它是矩形
6.下列命题中,正确的是(??? )
A.?在三角形中,到三角形三边距离相等的点是三条边垂直平分线的交点???
B.?平行四边形是轴对称图形???
C.?三角形的中位线将三角形分成面积相等的两个部分???
D.?一组对边平行,一组对角相等的四边形是平行四边形
7.如图,在平面直角坐标系中,四边形OABC是矩形,点O是坐标原点,点A、C的坐标分别是 (6,0) , (0,3) ,点B在第一象限,则点B的坐标是(?? )
A.?(3,6)???????????????????????????????????B.?(6,3)???????????????????????????????????C.?(6,6)???????????????????????????????????D.?(3,3)
8.菱形的周长为 8cm ,高为 1cm ,则该菱形两邻角度数比为(?? )
A.?5:1????????????????????????????????????????B.?4:1????????????????????????????????????????C.?3:1????????????????????????????????????????D.?2:1
9.如图,在?ABCD中,AB=6,BC=4,BE平分∠ABC,交CD于点E,则DE的长度是(?? )
A.?32??????????????????????????????????????????B.?2??????????????????????????????????????????C.?52??????????????????????????????????????????D.?3
10.如图,正方形 ABCD 的对角线 BD 长为 22 ,若直线 l 满足:①点 D 到直线 l 的距离为 3 ;② A,C 两点到直线 l 的距离相等,则正确的直线 l 的条数为(?? ?)
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
二、填空题
11.如图所示,在 ? ABCD中,∠A=50°,则∠B=________,∠C=________.
12.已知在四边形ABCD中, ∠A=∠B=∠C=90° ,若使四边形ABCD是正方形,则还需加上一个条件:________.
13.如图,在 ?ABCD 中,若 ∠A+∠C=140° , 则 ∠D 的大小为________.
14.正方形的对角线长为2,则正方形的边长为________cm.面积为________cm2.
15.菱形ABCD中,对角线AC长为10cm,BD=6cm,则菱形ABCD的面积为________cm2.
16.如图,已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是________.
17.如图,在菱形OABC中,点B在x轴上,点A的坐标为(2,3),则点C的坐标为________.
三、解答题
18.如图,□ABCD中对角线BD平分∠ABC.
求证:□ABCD是菱形.
19.如图,在□ABCD中,BE⊥CD,点E为垂足,AF=CE,求证:四边形BEDF是矩形.
20.如图,在平行四边形 ABCD 中, BE=DF .
求证: AE//CF .
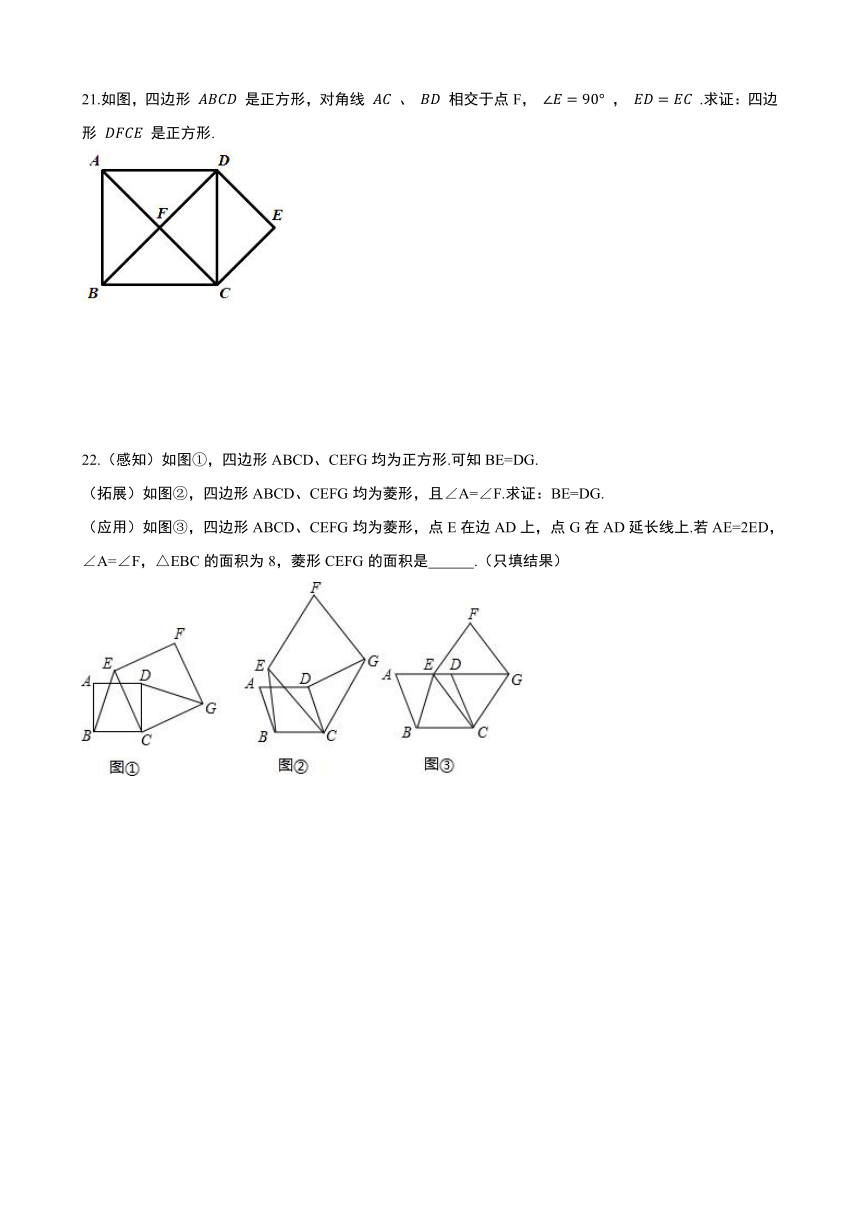
21.如图,四边形 ABCD 是正方形,对角线 AC 、 BD 相交于点F, ∠E=90° , ED=EC .求证:四边形 DFCE 是正方形.
22.(感知)如图①,四边形ABCD、CEFG均为正方形.可知BE=DG.
(拓展)如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.求证:BE=DG.
(应用)如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上.若AE=2ED,∠A=∠F,△EBC的面积为8,菱形CEFG的面积是?????????? .(只填结果)
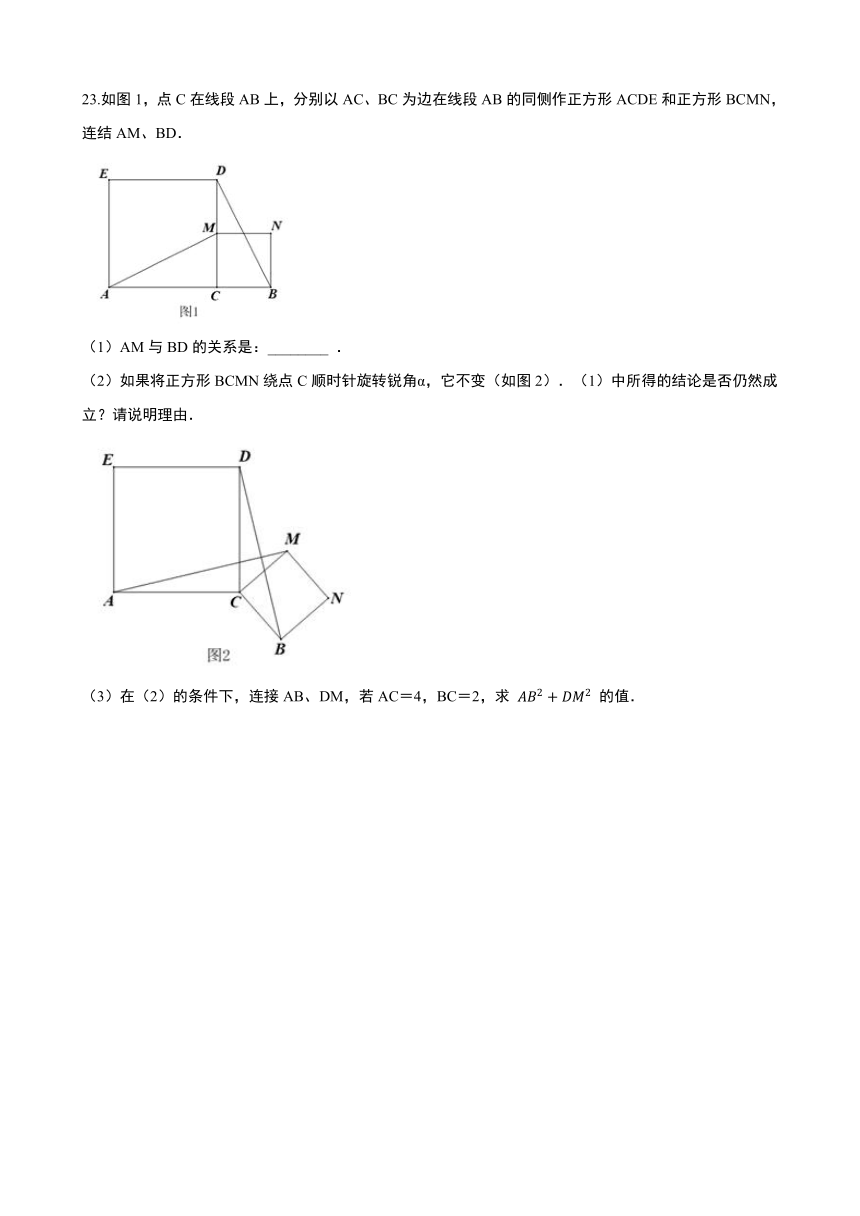
23.如图1,点C在线段AB上,分别以AC、BC为边在线段AB的同侧作正方形ACDE和正方形BCMN,连结AM、BD.
(1)AM与BD的关系是:________ .
(2)如果将正方形BCMN绕点C顺时针旋转锐角α,它不变(如图2).(1)中所得的结论是否仍然成立?请说明理由.
(3)在(2)的条件下,连接AB、DM,若AC=4,BC=2,求 AB2+DM2 的值.
参考答案
一、选择题
1.【答案】 B
解:∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,∠A+∠B=180°,
又∵∠A=2∠B,
∴2∠B+∠B=180°,
解得:∠B=60°,
∴∠D=60°;
故答案为:B.
2.【答案】 A
解:∵平行四边形、矩形、菱形、正方形的对角线互相平分
∴选项A正确;
∵菱形的对角线不相等
∴选项B错误;
∵矩形的对角线不相互垂直
∴选项C和D错误;
故答案为:A.
3.【答案】 C
解:矩形的对角线相等,对边平行且相等,对角也相等,
菱形的对角相等,对角线互相垂直平分,对边平行且相等,
于是可得矩形具有菱形不具有的性质是对角线相等,
故答案为:C.
4.【答案】 C
解:∵只有②③两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点,
∴带②③两块碎玻璃,就可以确定平行四边形的大小.
故答案为:C.
5.【答案】 C
解:A、?当AC⊥BD时,四边形ABCD是菱形,故A错误;
B、当AC=BD时,四边形ABCD是矩形,故B错误;
C、当∠ABC=90°时,四边形ABCD是矩形,故C正确;
D、 当AB=BC时,四边形ABCD是菱形,故D错误.
故答案为:C.
6.【答案】 D
解:A、在三角形中,到三角形三边距离相等的点是三条角平分线的交点 ,故A不符合题意;
B、 平行四边形是中心对称图形,不是轴对称图形,故B不符合题意;
C、 三角形的中线将三角形分成面积相等的两个部分 ,故C不符合题意;
D、 一组对边平行,一组对角相等的四边形是平行四边形,故D符合题意.
故答案为:D.
7.【答案】 B
解:∵四边形OABC是矩形,
∴OC=AB,CB=OA,
∵点A,C的坐标分别是(6,0),(0,3),
∴AB=3,OA=6,
∴点B坐标为(6,3),
故答案为:B.
8.【答案】 A
解:如图,DE是菱形ABCD的高,DE=1cm,
∵菱形ABCD的周长是 8cm ,
∴AD=2cm,
在Rt△ADE中,∵DE= 12 AD,∴∠A=30°,
∵AB∥DC,
∴∠A+∠ADC=180°,
∴∠ADC=150°,
∴∠ADC:∠A=150°:30°=5:1.
故答案为:A.
9.【答案】 B
解:∵四边形ABCD为平行四边形,
∴AB∥CD,CD=AB=6,
∴∠ABE=∠CEB,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠CBE=∠CEB,
∴CE=BC=4,
∴DE=CD﹣CE=6﹣4=2.
故答案为:B.
10.【答案】 B
解:如图,连接 AC 交 BD 于点 O ,
∵正方形 ABCD 的对角线BD为 22 ,
∴ OD=12BD=2 ,
∴满足点 D 到直线 l 的距离为 3 ,且点 A 、 C 到直线 l 的距离相等的直线,如图中的 l1(l1//AC) ,
根据对称性可知,在 D 的另一侧同样存在一条直线 l2 符合题意,
因此,正确的直线 l 有2条,
故答案为:B.
二、填空题
11.【答案】 130°;50°
解: ∵ ? ABCD,∠A=50°,
∴∠B=130°,∠C=50°.
故答案为:130°,50°.
12.【答案】 AB=BC (答案不唯一)
解:四边形ABCD中, ∠A=∠B=∠C=90° ,使得四边形ABCD是正方形还需加上一个 AB=BC 条件.理由如下:
∵∠A=∠B=∠C=90° ,
∴ 四边形ABCD是矩形,
又 ∵AB=BC ,
∴ 矩形ABCD是正方形.
故答案为: AB=BC( 答案不唯一 ) .
13.【答案】 110°
解:∵四边形 ABCD 是平行四边形
∴ ∠A=∠C , AB//CD
∵ ∠A+∠C=140°
∴ ∠A=∠C=70°
∴ ∠D=180°?∠A=110° .
故答案为:110°
14.【答案】 2;2
解:如图,正方形ABCD中,对角线AC=2,
由正方形的性质可知△ABC为等腰直角三角形,
∴AB=BC, AB2+BC2=AC2=4 ,
∴ AB=BC=2 ,S正方形=AB2=2,
故答案为: 2 ;2.
15.【答案】 30
解:菱形的面积等于两对角线的积的一半,则这个菱形的面积是6×10× 12 =30cm2.
故答案为:30.
16.【答案】 83
解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC= 12 AC= 12 ×4=2,∠BAC= 12 ∠BAD= 12 ×120°=60°,
∴AC=4,∠AOB=90°,
∴∠ABO=30°,
∴AB=2OA=4,OB= 23 ,
∴BD=2OB= 43 ,
∴该菱形的面积是: 12 AC?BD= 12 ×4× 43 = 83 ,
故答案为: 83 .
17.【答案】 (2,﹣3)
解:∵四边形OABC是菱形,
∴A、C关于直线OB对称,
∵A(2,3),
∴C(2,﹣3),
故答案为:(2,﹣3).
三、解答题
18.【答案】 证明:如图,
∵四边形ABCD是平行四边形
∴AD∥BC,
∴∠2=∠3.
又∵BD平分∠ABC,
∴∠1=∠2,
∴∠1=∠3,
∴ AB =AD,
∴□ABCD是菱形.
19.【答案】 解:由 ?ABCD 得,
AB∥DC,AB=DC,
又∵AF=CE,
∴ FB=AB-AF=DC-CE=DE,
又AB∥DC,即FB∥DE,
∴ 四边形BEDF是平行四边形,
又BE⊥CD,即∠BED=90°,
∴ 四边形BEDF是矩形.
20.【答案】 证明: ∵ 四边形 ABCD 是平行四边形,
∴AD//BC , AD=BC ,
∵BE=DF ,
∴AD?DF=BC?BE ,即 AF=EC ,
∵AF//EC , AF=EC ,
∴ 四边形 AECF 是平行四边形,、
∴AE//CF
21.【答案】 证明:∵四边形ABCD是正方形,
∴∠FDC=∠DCF=45°,
∵∠E=90°,ED=EC,
∴∠EDC=∠ECD=45°,
∴∠FCE=∠FDE=∠E=90°,
∴四边形DFCE是矩形,
∵DE=CE,
∴四边形DFCE是正方形.
22.【答案】 拓展:
证明:∵四边形ABCD、四边形CEFG均为菱形,
∴BC=CD,CE=CG,∠BCD=∠A,∠ECG=∠F.
∵∠A=∠F,
∴∠BCD=∠ECG.
∴∠BCD-∠ECD=∠ECG-∠ECD,
即∠BCE=∠DCG.
∴△BCE≌△DCG(SAS),
∴BE=DG.
应用:∵四边形ABCD为菱形,
∴AD∥BC,
∵BE=DG,
∴S△ABE+S△CDE=S△BEC=S△CDG=8,
∵AE= 2ED ,
∴S△CDE= 14×8=2 ?,
∴S△ECG=S△CDE+S△CDG=10
∴S菱形CEFG=2S△ECG=20.
23.【答案】 (1)相等且垂直
(2)成立,
理由:∵四边形ACDE正方形,四边形BCMN正方形,
∴AC=CD? ? MC=BC? ?∠ACD=∠BCM=90°,
∴?∠ACD+∠DCM=∠BCM+∠DCM,
即∠ACM=∠BCD,
∴△ACM≌△DCB(SAS),
∴AM=BD ,∠MAC=∠BDC,
同(1)可证AM⊥DB,
∴AM=BD且AM⊥DB.
(3)解:如图,
∵AM⊥DB,
∴∠DOM=∠AOB=∠AOD=∠BOM=90°,
由勾股定理得OD2+OM2=DM2 , OD2+OA2=AD2 , OB2+OM2=MB2 , OA2+OB2=AB2 ,
∴AB2+DM2=OD2+OM2+OA2+OB2=AD2+BM2 ,
∵AD=2AC=42 , BM=2BC=22?,
∴AB2+DM2=(42)2+(22)2=40.
一、选择题
1.在平行四边形 ABCD 中,若 ∠A=2∠B ,则 ∠D 的度数是(? )
A.?50°???????????????????????????????????????B.?60°???????????????????????????????????????C.?70°???????????????????????????????????????D.?80°
2.平行四边形、矩形、菱形、正方形共有的性质是(?? ).
A.?对角线互相平分?????????????B.?对角线相等?????????????C.?对角线互相垂直?????????????D.?对角形互相垂直平分
3.矩形具有而菱形不具有的性质是(?? )
A.?对角相等???????????????????????B.?对角线互相垂直???????????????????????C.?对角线相等???????????????????????D.?对边平行
4.小军不慎将一块平行四边形玻璃打碎成如图所示的四块,他带了两块碎玻璃到商店配成一块与原来相同的平行四边形玻璃,他带的碎玻璃编号是(?? )
A.?①②?????????????????????????????????????B.?①④?????????????????????????????????????C.?②③?????????????????????????????????????D.?②④
5.已知四边形ABCD是平行四边形,则下列结论中正确的是(?? )
A.?当AB⊥BD时,它是菱形 B.?当AC=BD时,它是正方形
C.?当∠ABC=90°时,它是矩形 D.?当AB=BC时,它是矩形
6.下列命题中,正确的是(??? )
A.?在三角形中,到三角形三边距离相等的点是三条边垂直平分线的交点???
B.?平行四边形是轴对称图形???
C.?三角形的中位线将三角形分成面积相等的两个部分???
D.?一组对边平行,一组对角相等的四边形是平行四边形
7.如图,在平面直角坐标系中,四边形OABC是矩形,点O是坐标原点,点A、C的坐标分别是 (6,0) , (0,3) ,点B在第一象限,则点B的坐标是(?? )
A.?(3,6)???????????????????????????????????B.?(6,3)???????????????????????????????????C.?(6,6)???????????????????????????????????D.?(3,3)
8.菱形的周长为 8cm ,高为 1cm ,则该菱形两邻角度数比为(?? )
A.?5:1????????????????????????????????????????B.?4:1????????????????????????????????????????C.?3:1????????????????????????????????????????D.?2:1
9.如图,在?ABCD中,AB=6,BC=4,BE平分∠ABC,交CD于点E,则DE的长度是(?? )
A.?32??????????????????????????????????????????B.?2??????????????????????????????????????????C.?52??????????????????????????????????????????D.?3
10.如图,正方形 ABCD 的对角线 BD 长为 22 ,若直线 l 满足:①点 D 到直线 l 的距离为 3 ;② A,C 两点到直线 l 的距离相等,则正确的直线 l 的条数为(?? ?)
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
二、填空题
11.如图所示,在 ? ABCD中,∠A=50°,则∠B=________,∠C=________.
12.已知在四边形ABCD中, ∠A=∠B=∠C=90° ,若使四边形ABCD是正方形,则还需加上一个条件:________.
13.如图,在 ?ABCD 中,若 ∠A+∠C=140° , 则 ∠D 的大小为________.
14.正方形的对角线长为2,则正方形的边长为________cm.面积为________cm2.
15.菱形ABCD中,对角线AC长为10cm,BD=6cm,则菱形ABCD的面积为________cm2.
16.如图,已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是________.
17.如图,在菱形OABC中,点B在x轴上,点A的坐标为(2,3),则点C的坐标为________.
三、解答题
18.如图,□ABCD中对角线BD平分∠ABC.
求证:□ABCD是菱形.
19.如图,在□ABCD中,BE⊥CD,点E为垂足,AF=CE,求证:四边形BEDF是矩形.
20.如图,在平行四边形 ABCD 中, BE=DF .
求证: AE//CF .
21.如图,四边形 ABCD 是正方形,对角线 AC 、 BD 相交于点F, ∠E=90° , ED=EC .求证:四边形 DFCE 是正方形.
22.(感知)如图①,四边形ABCD、CEFG均为正方形.可知BE=DG.
(拓展)如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.求证:BE=DG.
(应用)如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上.若AE=2ED,∠A=∠F,△EBC的面积为8,菱形CEFG的面积是?????????? .(只填结果)
23.如图1,点C在线段AB上,分别以AC、BC为边在线段AB的同侧作正方形ACDE和正方形BCMN,连结AM、BD.
(1)AM与BD的关系是:________ .
(2)如果将正方形BCMN绕点C顺时针旋转锐角α,它不变(如图2).(1)中所得的结论是否仍然成立?请说明理由.
(3)在(2)的条件下,连接AB、DM,若AC=4,BC=2,求 AB2+DM2 的值.
参考答案
一、选择题
1.【答案】 B
解:∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,∠A+∠B=180°,
又∵∠A=2∠B,
∴2∠B+∠B=180°,
解得:∠B=60°,
∴∠D=60°;
故答案为:B.
2.【答案】 A
解:∵平行四边形、矩形、菱形、正方形的对角线互相平分
∴选项A正确;
∵菱形的对角线不相等
∴选项B错误;
∵矩形的对角线不相互垂直
∴选项C和D错误;
故答案为:A.
3.【答案】 C
解:矩形的对角线相等,对边平行且相等,对角也相等,
菱形的对角相等,对角线互相垂直平分,对边平行且相等,
于是可得矩形具有菱形不具有的性质是对角线相等,
故答案为:C.
4.【答案】 C
解:∵只有②③两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点,
∴带②③两块碎玻璃,就可以确定平行四边形的大小.
故答案为:C.
5.【答案】 C
解:A、?当AC⊥BD时,四边形ABCD是菱形,故A错误;
B、当AC=BD时,四边形ABCD是矩形,故B错误;
C、当∠ABC=90°时,四边形ABCD是矩形,故C正确;
D、 当AB=BC时,四边形ABCD是菱形,故D错误.
故答案为:C.
6.【答案】 D
解:A、在三角形中,到三角形三边距离相等的点是三条角平分线的交点 ,故A不符合题意;
B、 平行四边形是中心对称图形,不是轴对称图形,故B不符合题意;
C、 三角形的中线将三角形分成面积相等的两个部分 ,故C不符合题意;
D、 一组对边平行,一组对角相等的四边形是平行四边形,故D符合题意.
故答案为:D.
7.【答案】 B
解:∵四边形OABC是矩形,
∴OC=AB,CB=OA,
∵点A,C的坐标分别是(6,0),(0,3),
∴AB=3,OA=6,
∴点B坐标为(6,3),
故答案为:B.
8.【答案】 A
解:如图,DE是菱形ABCD的高,DE=1cm,
∵菱形ABCD的周长是 8cm ,
∴AD=2cm,
在Rt△ADE中,∵DE= 12 AD,∴∠A=30°,
∵AB∥DC,
∴∠A+∠ADC=180°,
∴∠ADC=150°,
∴∠ADC:∠A=150°:30°=5:1.
故答案为:A.
9.【答案】 B
解:∵四边形ABCD为平行四边形,
∴AB∥CD,CD=AB=6,
∴∠ABE=∠CEB,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠CBE=∠CEB,
∴CE=BC=4,
∴DE=CD﹣CE=6﹣4=2.
故答案为:B.
10.【答案】 B
解:如图,连接 AC 交 BD 于点 O ,
∵正方形 ABCD 的对角线BD为 22 ,
∴ OD=12BD=2 ,
∴满足点 D 到直线 l 的距离为 3 ,且点 A 、 C 到直线 l 的距离相等的直线,如图中的 l1(l1//AC) ,
根据对称性可知,在 D 的另一侧同样存在一条直线 l2 符合题意,
因此,正确的直线 l 有2条,
故答案为:B.
二、填空题
11.【答案】 130°;50°
解: ∵ ? ABCD,∠A=50°,
∴∠B=130°,∠C=50°.
故答案为:130°,50°.
12.【答案】 AB=BC (答案不唯一)
解:四边形ABCD中, ∠A=∠B=∠C=90° ,使得四边形ABCD是正方形还需加上一个 AB=BC 条件.理由如下:
∵∠A=∠B=∠C=90° ,
∴ 四边形ABCD是矩形,
又 ∵AB=BC ,
∴ 矩形ABCD是正方形.
故答案为: AB=BC( 答案不唯一 ) .
13.【答案】 110°
解:∵四边形 ABCD 是平行四边形
∴ ∠A=∠C , AB//CD
∵ ∠A+∠C=140°
∴ ∠A=∠C=70°
∴ ∠D=180°?∠A=110° .
故答案为:110°
14.【答案】 2;2
解:如图,正方形ABCD中,对角线AC=2,
由正方形的性质可知△ABC为等腰直角三角形,
∴AB=BC, AB2+BC2=AC2=4 ,
∴ AB=BC=2 ,S正方形=AB2=2,
故答案为: 2 ;2.
15.【答案】 30
解:菱形的面积等于两对角线的积的一半,则这个菱形的面积是6×10× 12 =30cm2.
故答案为:30.
16.【答案】 83
解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC= 12 AC= 12 ×4=2,∠BAC= 12 ∠BAD= 12 ×120°=60°,
∴AC=4,∠AOB=90°,
∴∠ABO=30°,
∴AB=2OA=4,OB= 23 ,
∴BD=2OB= 43 ,
∴该菱形的面积是: 12 AC?BD= 12 ×4× 43 = 83 ,
故答案为: 83 .
17.【答案】 (2,﹣3)
解:∵四边形OABC是菱形,
∴A、C关于直线OB对称,
∵A(2,3),
∴C(2,﹣3),
故答案为:(2,﹣3).
三、解答题
18.【答案】 证明:如图,
∵四边形ABCD是平行四边形
∴AD∥BC,
∴∠2=∠3.
又∵BD平分∠ABC,
∴∠1=∠2,
∴∠1=∠3,
∴ AB =AD,
∴□ABCD是菱形.
19.【答案】 解:由 ?ABCD 得,
AB∥DC,AB=DC,
又∵AF=CE,
∴ FB=AB-AF=DC-CE=DE,
又AB∥DC,即FB∥DE,
∴ 四边形BEDF是平行四边形,
又BE⊥CD,即∠BED=90°,
∴ 四边形BEDF是矩形.
20.【答案】 证明: ∵ 四边形 ABCD 是平行四边形,
∴AD//BC , AD=BC ,
∵BE=DF ,
∴AD?DF=BC?BE ,即 AF=EC ,
∵AF//EC , AF=EC ,
∴ 四边形 AECF 是平行四边形,、
∴AE//CF
21.【答案】 证明:∵四边形ABCD是正方形,
∴∠FDC=∠DCF=45°,
∵∠E=90°,ED=EC,
∴∠EDC=∠ECD=45°,
∴∠FCE=∠FDE=∠E=90°,
∴四边形DFCE是矩形,
∵DE=CE,
∴四边形DFCE是正方形.
22.【答案】 拓展:
证明:∵四边形ABCD、四边形CEFG均为菱形,
∴BC=CD,CE=CG,∠BCD=∠A,∠ECG=∠F.
∵∠A=∠F,
∴∠BCD=∠ECG.
∴∠BCD-∠ECD=∠ECG-∠ECD,
即∠BCE=∠DCG.
∴△BCE≌△DCG(SAS),
∴BE=DG.
应用:∵四边形ABCD为菱形,
∴AD∥BC,
∵BE=DG,
∴S△ABE+S△CDE=S△BEC=S△CDG=8,
∵AE= 2ED ,
∴S△CDE= 14×8=2 ?,
∴S△ECG=S△CDE+S△CDG=10
∴S菱形CEFG=2S△ECG=20.
23.【答案】 (1)相等且垂直
(2)成立,
理由:∵四边形ACDE正方形,四边形BCMN正方形,
∴AC=CD? ? MC=BC? ?∠ACD=∠BCM=90°,
∴?∠ACD+∠DCM=∠BCM+∠DCM,
即∠ACM=∠BCD,
∴△ACM≌△DCB(SAS),
∴AM=BD ,∠MAC=∠BDC,
同(1)可证AM⊥DB,
∴AM=BD且AM⊥DB.
(3)解:如图,
∵AM⊥DB,
∴∠DOM=∠AOB=∠AOD=∠BOM=90°,
由勾股定理得OD2+OM2=DM2 , OD2+OA2=AD2 , OB2+OM2=MB2 , OA2+OB2=AB2 ,
∴AB2+DM2=OD2+OM2+OA2+OB2=AD2+BM2 ,
∵AD=2AC=42 , BM=2BC=22?,
∴AB2+DM2=(42)2+(22)2=40.
