18.2.2菱形的性质 同步练习(含答案)
文档属性
| 名称 | 18.2.2菱形的性质 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-29 08:54:51 | ||
图片预览



文档简介
125984001235710018.2.2菱形的性质同步练习
一、单选题
1.下列结论中,矩形具有而菱形不一定具有的性质是( )
A.内角和为360° B.对角线互相平分 C.对角线相等 D.对角线互相垂直
2.如图,已知某广场菱形花坛ABCD的周长是24米,∠BAD=60°,则花坛对角线AC的长等于( )
A.6false米 B.6米 C.3false米 D.3米
3.菱形不具备的性质是( )
A.四条边都相等 B.对角线一定相等 C.是轴对称图形 D.是中心对称图形
4.如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )
A.2.4cm B.4.8cm C.5cm D.9.6cm
5.如图,菱形ABCD的对角线AC、BD的长分别为6和8,则这个菱形的周长是( )
A.20 B.24 C.40 D.48
6.如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有(??? ).
A.1个 B.2个 C.3个 D.4个
7.如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为( )
A.(1,-1) B.(-1,-1) C.(false,0) D.(0,-false)
8.如图,在菱形false中,对角线false与false相交于点false,false,垂足为false,若false,则false的大小为( )
A.75° B.65°
C.55° D.50°
9.如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.给出如下几个结论:
①∠ADE=∠DBF;②△DAE≌△BDG;③若AF=2DF,则BG=6GF;④CG与BD一定不垂直;⑤∠BGE=60°.其中正确的结论个数为( )
A.5 B.4 C.3 D.2
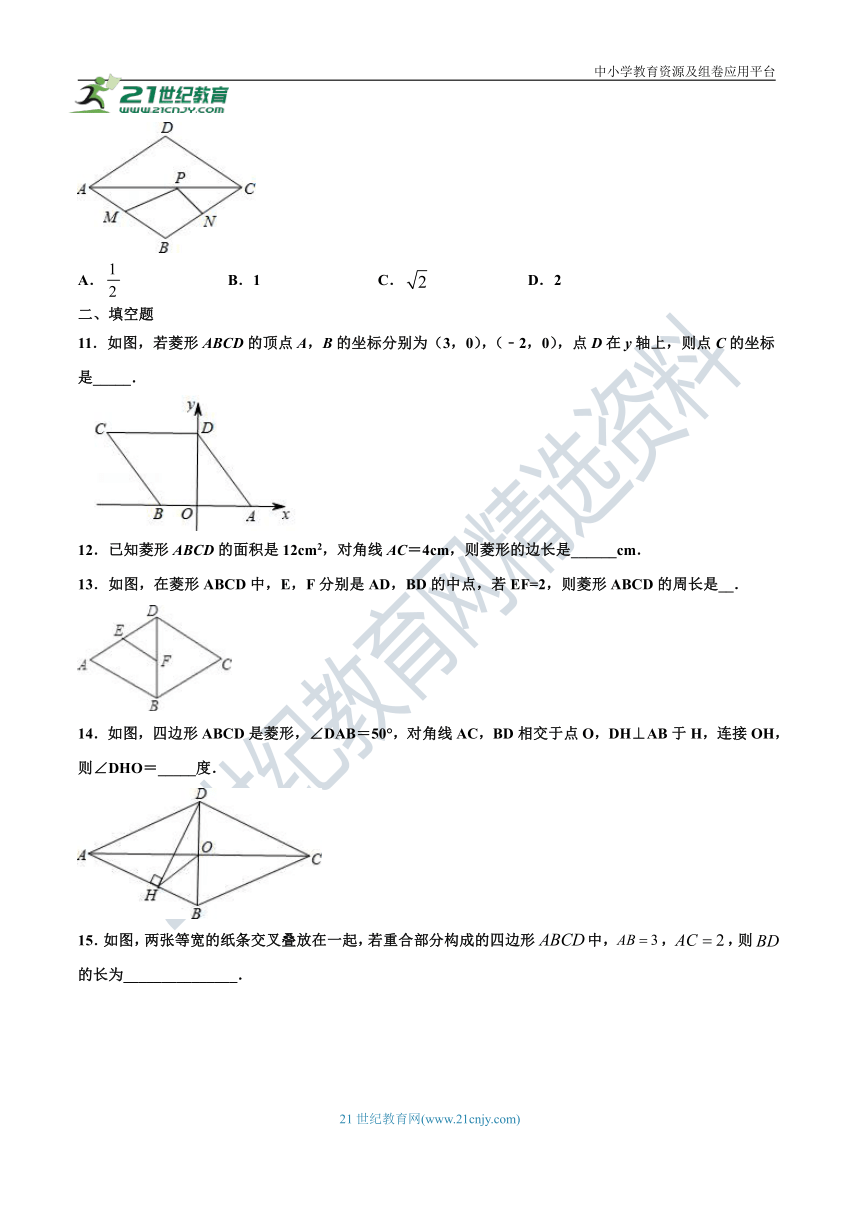
10.如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是( )
A.false B.1 C.false D.2
二、填空题
11.如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),(﹣2,0),点D在y轴上,则点C的坐标是_____.
12.已知菱形ABCD的面积是12cm2,对角线AC=4cm,则菱形的边长是______cm.
13.如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=2,则菱形ABCD的周长是__.
14.如图,四边形ABCD是菱形,∠DAB=50°,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,则∠DHO=_____度.
15.如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形false中,false,false,则false的长为_______________.
16.如图,已知菱形ABCD的周长为16,面积为false,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为______.
三、解答题
17.如图,已知A、F、C、D四点在同一条直线上,AF=CD,AB∥DE,且AB=DE
(1)求证:△ABC≌△DEF;
(2)若EF=3,DE=4,∠DEF=90°,请直接写出使四边形EFBC为菱形时AF的长度.
18.如图,矩形ABCD中,O是对角线AC的中点,延长AB到G,使BG=AB,连接GO并延长,交BC于E,交AD于F,且AC=2AB,连接AE、CF.求证:四边形AECF是菱形.
19.如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:false;
(2)若AB=2,false,当四边形ADFC是菱形时,求BF的长.
答案
一、单选题
1.C 2.A 3.B 4.B 5.A 6.D. 7.B 8.B 9.C 10.B
二、填空题
11.(﹣5,4).
12.false
13.16
14.25.
15.4false
16.false.
三、解答题
17.【详解】(1)∵AB∥DE,
∴∠A=∠D,
∵AF=CD,
∴AF+FC=CD+FC,
即AC=DF,
∵AB=DE,
∴△ABC≌△DEF;
(2)如图,连接AB交AD于O,
在Rt△EFD中,∵∠DEF=90°,EF=3,DE=4,
∴DF=false=5,
∵四边形EFBC是菱形,
∴BE⊥CF,∴EO=false,
∴OF=OC=false,
∴CF=false,
∴AF=CD=DF﹣FC=5﹣false=false.
18.【详解】
证明:连接CG,
∵在矩形ABCD中AC=2AB,
∴∠CAG=60°,
∵BG=AB,
∴AG=AC,
∴△ACG是等边三角形,
∵O为AC的中点,
∴GF⊥AC,
∵在矩形ABCD中,BC‖AD,
∴∠DAC=∠BCA,AO=OC,∠AOF=∠COE=90°,
∴△AOF≌△COE,
∴CE=AF,
∴四边形AECF是平行四边形,
∴四边形AECF是菱形(对角线互相垂直的平行四边形是菱形).
19.【详解】
解析:(1)∵△ABC≌△ADE且AB=AC
∴AE=AD,AB=AC
∠BAC+∠BAE=∠DAE+∠BAE
∴∠CAE=∠DAB
∴△AEC≌△ADB
(3)∵四边形ADFC是菱形且∠BAC=45°
∴∠DBA=∠BAC=45°
由(1)得AB=AD
∴∠DBA=∠BDA=45°
∴△ABD是直角边长为2的等腰直角三角形
∴BD=2false
又∵四边形ADFC是菱形
∴AD=DF=FC=AC=AB=2
∴BF=BD-DF=2false-2
20.:解:(1)结论AE=EF=AF.
理由:如图1中,连接AC,∵四边形ABCD是菱形,∠B=60°,∴AB=BC=CD=AD,∠B=∠D=60°,∴△ABC,△ADC是等边三角形,∴∠BAC=∠DAC=60°.∵BE=EC,∴∠BAE=∠CAE=30°,AE⊥BC.∵∠EAF=60°,∴∠CAF=∠DAF=30°,∴AF⊥CD,∴AE=AF(菱形的高相等),∴△AEF是等边三角形,∴AE=EF=AF.
(2)连接AC.如图2中,∵∠BAC=∠EAF=60°,∴∠BAE=∠CAE,在△BAE和△CAF中,∵∠BAE=∠CAF,BA=AC,∠B=∠ACF,∴△BAE≌△CAF,∴BE=CF.
(3)过点A作AG⊥BC于点G,过点F作FH⊥EC于点H.∵∠EAB=15°,∠ABC=60°,∴∠AEB=45°.在Rt△AGB中,∵∠ABC=60°AB=4,∴BG=2,AG=23.在Rt△AEG中,∵∠AEG=∠EAG=45°,∴AG=GE=23,∴EB=EG﹣BG=23?2.∵△AEB≌△AFC,∴AE=AF,EB=CF=23?2,∠AEB=∠AFC=45°.∵∠EAF=60°,AE=AF,∴△AEF是等边三角形,∴∠AEF=∠AFE=60°.
∵∠AEB=45°,∠AEF=60°,∴∠CEF=∠AEF﹣∠AEB=15°.在Rt△EFH中,∠CEF=15°,∴∠EFH=75°.∵∠AFE=60°,∴∠AFH=∠EFH﹣∠AFE=15°.∵∠AFC=45°,∴∠CFH=∠AFC﹣∠AFH=30°.在Rt△CHF中,∵∠CFH=30°,CF=23?2,∴FH=CF?sin60°=(23?2)×32=3?3,∴点F到BC的距离为3?3.
一、单选题
1.下列结论中,矩形具有而菱形不一定具有的性质是( )
A.内角和为360° B.对角线互相平分 C.对角线相等 D.对角线互相垂直
2.如图,已知某广场菱形花坛ABCD的周长是24米,∠BAD=60°,则花坛对角线AC的长等于( )
A.6false米 B.6米 C.3false米 D.3米
3.菱形不具备的性质是( )
A.四条边都相等 B.对角线一定相等 C.是轴对称图形 D.是中心对称图形
4.如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )
A.2.4cm B.4.8cm C.5cm D.9.6cm
5.如图,菱形ABCD的对角线AC、BD的长分别为6和8,则这个菱形的周长是( )
A.20 B.24 C.40 D.48
6.如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有(??? ).
A.1个 B.2个 C.3个 D.4个
7.如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为( )
A.(1,-1) B.(-1,-1) C.(false,0) D.(0,-false)
8.如图,在菱形false中,对角线false与false相交于点false,false,垂足为false,若false,则false的大小为( )
A.75° B.65°
C.55° D.50°
9.如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.给出如下几个结论:
①∠ADE=∠DBF;②△DAE≌△BDG;③若AF=2DF,则BG=6GF;④CG与BD一定不垂直;⑤∠BGE=60°.其中正确的结论个数为( )
A.5 B.4 C.3 D.2
10.如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是( )
A.false B.1 C.false D.2
二、填空题
11.如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),(﹣2,0),点D在y轴上,则点C的坐标是_____.
12.已知菱形ABCD的面积是12cm2,对角线AC=4cm,则菱形的边长是______cm.
13.如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=2,则菱形ABCD的周长是__.
14.如图,四边形ABCD是菱形,∠DAB=50°,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,则∠DHO=_____度.
15.如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形false中,false,false,则false的长为_______________.
16.如图,已知菱形ABCD的周长为16,面积为false,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为______.
三、解答题
17.如图,已知A、F、C、D四点在同一条直线上,AF=CD,AB∥DE,且AB=DE
(1)求证:△ABC≌△DEF;
(2)若EF=3,DE=4,∠DEF=90°,请直接写出使四边形EFBC为菱形时AF的长度.
18.如图,矩形ABCD中,O是对角线AC的中点,延长AB到G,使BG=AB,连接GO并延长,交BC于E,交AD于F,且AC=2AB,连接AE、CF.求证:四边形AECF是菱形.
19.如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:false;
(2)若AB=2,false,当四边形ADFC是菱形时,求BF的长.
答案
一、单选题
1.C 2.A 3.B 4.B 5.A 6.D. 7.B 8.B 9.C 10.B
二、填空题
11.(﹣5,4).
12.false
13.16
14.25.
15.4false
16.false.
三、解答题
17.【详解】(1)∵AB∥DE,
∴∠A=∠D,
∵AF=CD,
∴AF+FC=CD+FC,
即AC=DF,
∵AB=DE,
∴△ABC≌△DEF;
(2)如图,连接AB交AD于O,
在Rt△EFD中,∵∠DEF=90°,EF=3,DE=4,
∴DF=false=5,
∵四边形EFBC是菱形,
∴BE⊥CF,∴EO=false,
∴OF=OC=false,
∴CF=false,
∴AF=CD=DF﹣FC=5﹣false=false.
18.【详解】
证明:连接CG,
∵在矩形ABCD中AC=2AB,
∴∠CAG=60°,
∵BG=AB,
∴AG=AC,
∴△ACG是等边三角形,
∵O为AC的中点,
∴GF⊥AC,
∵在矩形ABCD中,BC‖AD,
∴∠DAC=∠BCA,AO=OC,∠AOF=∠COE=90°,
∴△AOF≌△COE,
∴CE=AF,
∴四边形AECF是平行四边形,
∴四边形AECF是菱形(对角线互相垂直的平行四边形是菱形).
19.【详解】
解析:(1)∵△ABC≌△ADE且AB=AC
∴AE=AD,AB=AC
∠BAC+∠BAE=∠DAE+∠BAE
∴∠CAE=∠DAB
∴△AEC≌△ADB
(3)∵四边形ADFC是菱形且∠BAC=45°
∴∠DBA=∠BAC=45°
由(1)得AB=AD
∴∠DBA=∠BDA=45°
∴△ABD是直角边长为2的等腰直角三角形
∴BD=2false
又∵四边形ADFC是菱形
∴AD=DF=FC=AC=AB=2
∴BF=BD-DF=2false-2
20.:解:(1)结论AE=EF=AF.
理由:如图1中,连接AC,∵四边形ABCD是菱形,∠B=60°,∴AB=BC=CD=AD,∠B=∠D=60°,∴△ABC,△ADC是等边三角形,∴∠BAC=∠DAC=60°.∵BE=EC,∴∠BAE=∠CAE=30°,AE⊥BC.∵∠EAF=60°,∴∠CAF=∠DAF=30°,∴AF⊥CD,∴AE=AF(菱形的高相等),∴△AEF是等边三角形,∴AE=EF=AF.
(2)连接AC.如图2中,∵∠BAC=∠EAF=60°,∴∠BAE=∠CAE,在△BAE和△CAF中,∵∠BAE=∠CAF,BA=AC,∠B=∠ACF,∴△BAE≌△CAF,∴BE=CF.
(3)过点A作AG⊥BC于点G,过点F作FH⊥EC于点H.∵∠EAB=15°,∠ABC=60°,∴∠AEB=45°.在Rt△AGB中,∵∠ABC=60°AB=4,∴BG=2,AG=23.在Rt△AEG中,∵∠AEG=∠EAG=45°,∴AG=GE=23,∴EB=EG﹣BG=23?2.∵△AEB≌△AFC,∴AE=AF,EB=CF=23?2,∠AEB=∠AFC=45°.∵∠EAF=60°,AE=AF,∴△AEF是等边三角形,∴∠AEF=∠AFE=60°.
∵∠AEB=45°,∠AEF=60°,∴∠CEF=∠AEF﹣∠AEB=15°.在Rt△EFH中,∠CEF=15°,∴∠EFH=75°.∵∠AFE=60°,∴∠AFH=∠EFH﹣∠AFE=15°.∵∠AFC=45°,∴∠CFH=∠AFC﹣∠AFH=30°.在Rt△CHF中,∵∠CFH=30°,CF=23?2,∴FH=CF?sin60°=(23?2)×32=3?3,∴点F到BC的距离为3?3.
