18.2.3正方形 同步练习(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
18.2.3正方形同步练习
一、单选题
1.关于?ABCD的叙述,正确的是( )
A.若AB⊥BC,则?ABCD是菱形 B.若AC⊥BD,则ABCD是正方形
C.若AC=BD,则?ABCD是矩形 D.若AB=AD,则?ABCD是正方形
2.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是( )
A.AC=BD,AB∥CD,AB=CD B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD D.AO=CO,BO=DO,AB=BC
3.下列命题正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.一组邻边相等的矩形是正方形
4.下列命题中正确的是( )
A.有一组邻边相等的四边形是菱形
B.有一个角是直角的平行四边形是矩形
C.对角线垂直的平行四边形是正方形
D.一组对边平行的四边形是平行四边形
5.如图,边长相等的两个正方形ABCD和OEFG,若将正方形OEFG绕点O按逆时针方向旋转150°,两个正方形的重叠部分四边形OMCN的面积( )
A.不变 B.先增大再减小 C.先减小再增大 D.不断增大
6.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为( )
A.3 B.4 C. D.
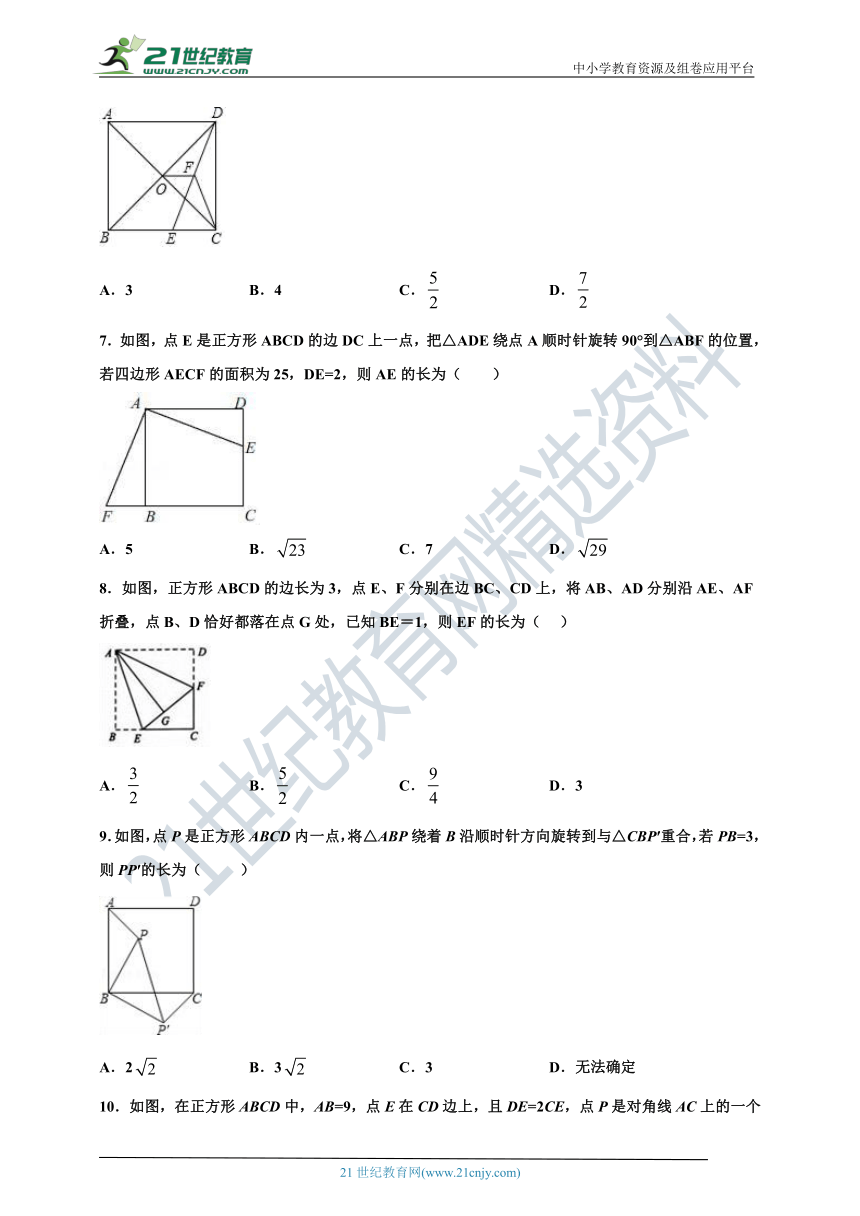
7.如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=2,则AE的长为( )
A.5 B. C.7 D.
8.如图,正方形ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B、D恰好都落在点G处,已知BE=1,则EF的长为(??? )
A. B. C. D.3
9.如图,点P是正方形ABCD内一点,将△ABP绕着B沿顺时针方向旋转到与△CBP′重合,若PB=3,则PP′的长为( )
A.2 B.3 C.3 D.无法确定
10.如图,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值是( )
A. B. C.9 D.
二、填空题
11.如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为__________.
12.如图,在正方形的外侧,作等边,则的度数是__________.
13.如图,中,交于,交于,是的角平分线,那么四边形的形状是________形;在前面的条件下,若再满足一个条件________,则四边形是正方形.
14.如图,在中,,点分别是边的中点,延长到点,使,得四边形.若使四边形是正方形,则应在中再添加一个条件为__________.
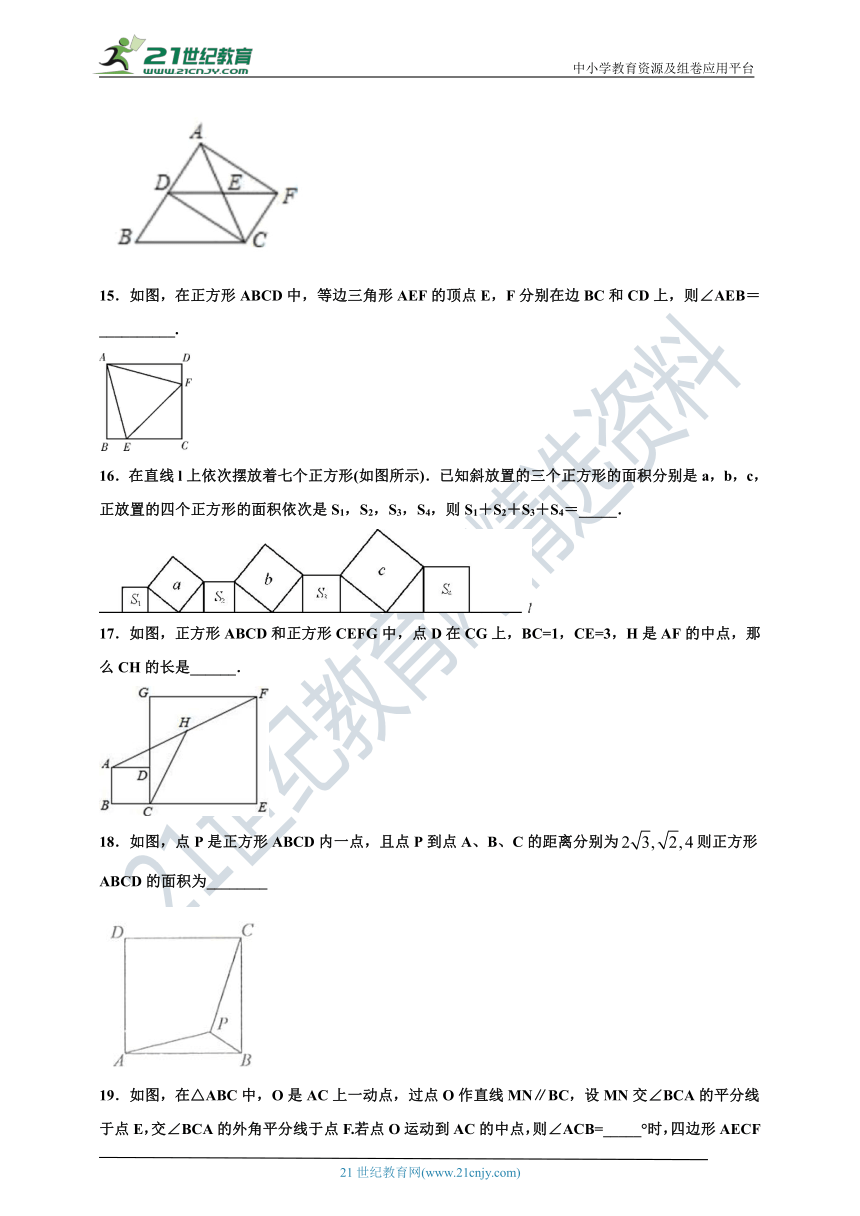
15.如图,在正方形ABCD中,等边三角形AEF的顶点E,F分别在边BC和CD上,则∠AEB=__________.
16.在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是a,b,c,正放置的四个正方形的面积依次是S1,S2,S3,S4,则S1+S2+S3+S4=_____.
17.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是______.
18.如图,点P是正方形ABCD内一点,且点P到点A、B、C的距离分别为则正方形ABCD的面积为________
19.如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.若点O运动到AC的中点,则∠ACB=_____°时,四边形AECF是正方形.
20.在正方形ABCD中,E在AB上,BE=2,AE=1,P是BD上的动点,则PE和PA的长度之和最小值为___________.
三、解答题
21.如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE,
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
22.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
23.如图,已知△ABC,点A在BC边的上方,把△ABC绕点B逆时针方向旋转60°得△DBE,绕点C顺时针方向旋转60°得△FEC,连接AD,AF.
(1)△ABD,△ACF,△BCE是什么特殊三角形?请说明理由;
(2)当△ABC满足什么条件时,四边形ADEF是正方形?请说明理由;
(3)当△ABC满足什么条件时,以点A,D,E,F为顶点的四边形不存在?请说明理由.
24.如图,(图1,图2),四边形ABCD是边长为4的正方形,点E在线段BC上,∠AEF=90°,且EF交正方形外角平分线CP于点F,交BC的延长线于点N, FN⊥BC.
(1)若点E是BC的中点(如图1),AE与EF相等吗?
(2)点E在BC间运动时(如图2),设BE=x,△ECF的面积为y.
①求y与x的函数关系式;
②当x取何值时,y有最大值,并求出这个最大值.
答案
一、单选题
1.C 2.C 3.D 4.B 5.A 6.D 7.D 8.B 9.B 10.A
二、填空题
11.6
12.
13.菱
14.答案不唯一,如∠ACB=90° 或∠BAC=45°或∠B=45°
15.75
16.a+c
17.
18.
19.90
20.
三、解答题
21.【答案】解:(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,
∴四边形AEBD是平行四边形.
∵AB=AC,AD是△ABC的角平分线,∴AD⊥BC.
∴∠ADB=90°.
∴平行四边形AEBD是矩形.
(2)当∠BAC=90°时,矩形AEBD是正方形.理由如下:
∵∠BAC=90°,AB=AC,AD是△ABC的角平分线,∴AD=BD=CD.
∵由(1)得四边形AEBD是矩形,∴矩形AEBD是正方形.
22.【详解】
(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD(直角三角形斜边上的中线等于斜边的一半),
∴四边形BECD是菱形;
(3)当∠A=45°时,四边形BECD是正方形,理由是:
解:∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,
∴AC=BC,
∵D为BA中点,
∴CD⊥AB,
∴∠CDB=90°,
∵四边形BECD是菱形,
∴菱形BECD是正方形,
即当∠A=45°时,四边形BECD是正方形.
23.【详解】
(1)△ABD,△ACF,△BCE都是等边三角形,
理由:由旋转可知:AB=DB,∠ABD=60°,
AC=FC,∠ACF=60°;BC=BE,∠CBE=60°,
∴△ABD,△ACF,△BCE都是等边三角形;
(2)当∠BAC=150°,且AB=AC时,四边形ADEF是正方形,
理由:∵△DBE是由△ABC绕点B旋转60°而得到的,∴DE=AC,
由(1)知△ACF为等边三角形,
∴AC=AF,∴DE=AF,
同理可得EF=AD,
∴四边形ADEF是平行四边形,
若∠BAC=150°,则∠DAF=360°-∠BAC-∠DAB-∠FAC=360°-150°-60°-60°=90°,
∴四边形ADEF是矩形,
又∵AB=AC,∴AD=AF,
则四边形ADEF是正方形;
(3)当∠BAC=60°时,以点A,D,E,F为顶点的四边形不存在,
理由:若∠BAC=60°,则∠DAF=360°-∠BAC-∠DAB-∠FAC=360°-60°-60°-60°=180°,
此时,点A,D,E,F四点共线,
∴以点A,D,E,F为顶点的四边形不存在.
24.【详解】
(1)如图,在AB上取AG=EC,
∵四边形ABCD是正方形,
∴AB=BC,
有∵AG=EC ,∴BG=BE ,
又∵∠B=90°,
∴∠AGE=135°,
又∵∠BCD=90°,CP平分∠DCN,
∴∠ECF=135°,
∵∠BAE+∠AEB=90°,∠AEB+∠FEC=90°,
∴∠BAE=∠FEC,
在△AGE和△ECF中,
,
∴△AGE≌△ECF,
∴AE=EF;
(2)①∵由(1)证明可知当E不是中点时同理可证AE=EF,
∵∠BAE=∠NEF,∠B=∠ENF=90°,
∴△ABE≌△ENF,
∴FN=BE=x,
∴S△ECF= (BC-BE)·FN,
即y= x(4-x),
∴y=- x2+2x(0<x<4),
②,
当x=2,y最大值=2.
_21?????????è?????(www.21cnjy.com)_
18.2.3正方形同步练习
一、单选题
1.关于?ABCD的叙述,正确的是( )
A.若AB⊥BC,则?ABCD是菱形 B.若AC⊥BD,则ABCD是正方形
C.若AC=BD,则?ABCD是矩形 D.若AB=AD,则?ABCD是正方形
2.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是( )
A.AC=BD,AB∥CD,AB=CD B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD D.AO=CO,BO=DO,AB=BC
3.下列命题正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.一组邻边相等的矩形是正方形
4.下列命题中正确的是( )
A.有一组邻边相等的四边形是菱形
B.有一个角是直角的平行四边形是矩形
C.对角线垂直的平行四边形是正方形
D.一组对边平行的四边形是平行四边形
5.如图,边长相等的两个正方形ABCD和OEFG,若将正方形OEFG绕点O按逆时针方向旋转150°,两个正方形的重叠部分四边形OMCN的面积( )
A.不变 B.先增大再减小 C.先减小再增大 D.不断增大
6.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为( )
A.3 B.4 C. D.
7.如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=2,则AE的长为( )
A.5 B. C.7 D.
8.如图,正方形ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B、D恰好都落在点G处,已知BE=1,则EF的长为(??? )
A. B. C. D.3
9.如图,点P是正方形ABCD内一点,将△ABP绕着B沿顺时针方向旋转到与△CBP′重合,若PB=3,则PP′的长为( )
A.2 B.3 C.3 D.无法确定
10.如图,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值是( )
A. B. C.9 D.
二、填空题
11.如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为__________.
12.如图,在正方形的外侧,作等边,则的度数是__________.
13.如图,中,交于,交于,是的角平分线,那么四边形的形状是________形;在前面的条件下,若再满足一个条件________,则四边形是正方形.
14.如图,在中,,点分别是边的中点,延长到点,使,得四边形.若使四边形是正方形,则应在中再添加一个条件为__________.
15.如图,在正方形ABCD中,等边三角形AEF的顶点E,F分别在边BC和CD上,则∠AEB=__________.
16.在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是a,b,c,正放置的四个正方形的面积依次是S1,S2,S3,S4,则S1+S2+S3+S4=_____.
17.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是______.
18.如图,点P是正方形ABCD内一点,且点P到点A、B、C的距离分别为则正方形ABCD的面积为________
19.如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.若点O运动到AC的中点,则∠ACB=_____°时,四边形AECF是正方形.
20.在正方形ABCD中,E在AB上,BE=2,AE=1,P是BD上的动点,则PE和PA的长度之和最小值为___________.
三、解答题
21.如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE,
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
22.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
23.如图,已知△ABC,点A在BC边的上方,把△ABC绕点B逆时针方向旋转60°得△DBE,绕点C顺时针方向旋转60°得△FEC,连接AD,AF.
(1)△ABD,△ACF,△BCE是什么特殊三角形?请说明理由;
(2)当△ABC满足什么条件时,四边形ADEF是正方形?请说明理由;
(3)当△ABC满足什么条件时,以点A,D,E,F为顶点的四边形不存在?请说明理由.
24.如图,(图1,图2),四边形ABCD是边长为4的正方形,点E在线段BC上,∠AEF=90°,且EF交正方形外角平分线CP于点F,交BC的延长线于点N, FN⊥BC.
(1)若点E是BC的中点(如图1),AE与EF相等吗?
(2)点E在BC间运动时(如图2),设BE=x,△ECF的面积为y.
①求y与x的函数关系式;
②当x取何值时,y有最大值,并求出这个最大值.
答案
一、单选题
1.C 2.C 3.D 4.B 5.A 6.D 7.D 8.B 9.B 10.A
二、填空题
11.6
12.
13.菱
14.答案不唯一,如∠ACB=90° 或∠BAC=45°或∠B=45°
15.75
16.a+c
17.
18.
19.90
20.
三、解答题
21.【答案】解:(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,
∴四边形AEBD是平行四边形.
∵AB=AC,AD是△ABC的角平分线,∴AD⊥BC.
∴∠ADB=90°.
∴平行四边形AEBD是矩形.
(2)当∠BAC=90°时,矩形AEBD是正方形.理由如下:
∵∠BAC=90°,AB=AC,AD是△ABC的角平分线,∴AD=BD=CD.
∵由(1)得四边形AEBD是矩形,∴矩形AEBD是正方形.
22.【详解】
(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD(直角三角形斜边上的中线等于斜边的一半),
∴四边形BECD是菱形;
(3)当∠A=45°时,四边形BECD是正方形,理由是:
解:∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,
∴AC=BC,
∵D为BA中点,
∴CD⊥AB,
∴∠CDB=90°,
∵四边形BECD是菱形,
∴菱形BECD是正方形,
即当∠A=45°时,四边形BECD是正方形.
23.【详解】
(1)△ABD,△ACF,△BCE都是等边三角形,
理由:由旋转可知:AB=DB,∠ABD=60°,
AC=FC,∠ACF=60°;BC=BE,∠CBE=60°,
∴△ABD,△ACF,△BCE都是等边三角形;
(2)当∠BAC=150°,且AB=AC时,四边形ADEF是正方形,
理由:∵△DBE是由△ABC绕点B旋转60°而得到的,∴DE=AC,
由(1)知△ACF为等边三角形,
∴AC=AF,∴DE=AF,
同理可得EF=AD,
∴四边形ADEF是平行四边形,
若∠BAC=150°,则∠DAF=360°-∠BAC-∠DAB-∠FAC=360°-150°-60°-60°=90°,
∴四边形ADEF是矩形,
又∵AB=AC,∴AD=AF,
则四边形ADEF是正方形;
(3)当∠BAC=60°时,以点A,D,E,F为顶点的四边形不存在,
理由:若∠BAC=60°,则∠DAF=360°-∠BAC-∠DAB-∠FAC=360°-60°-60°-60°=180°,
此时,点A,D,E,F四点共线,
∴以点A,D,E,F为顶点的四边形不存在.
24.【详解】
(1)如图,在AB上取AG=EC,
∵四边形ABCD是正方形,
∴AB=BC,
有∵AG=EC ,∴BG=BE ,
又∵∠B=90°,
∴∠AGE=135°,
又∵∠BCD=90°,CP平分∠DCN,
∴∠ECF=135°,
∵∠BAE+∠AEB=90°,∠AEB+∠FEC=90°,
∴∠BAE=∠FEC,
在△AGE和△ECF中,
,
∴△AGE≌△ECF,
∴AE=EF;
(2)①∵由(1)证明可知当E不是中点时同理可证AE=EF,
∵∠BAE=∠NEF,∠B=∠ENF=90°,
∴△ABE≌△ENF,
∴FN=BE=x,
∴S△ECF= (BC-BE)·FN,
即y= x(4-x),
∴y=- x2+2x(0<x<4),
②,
当x=2,y最大值=2.
_21?????????è?????(www.21cnjy.com)_
