六年级数学下册课件-7.1.11式与方程 苏教版(共 22 张ppt)
文档属性
| 名称 | 六年级数学下册课件-7.1.11式与方程 苏教版(共 22 张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-28 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
总复习:式与方程
苏教版六年级数学下册
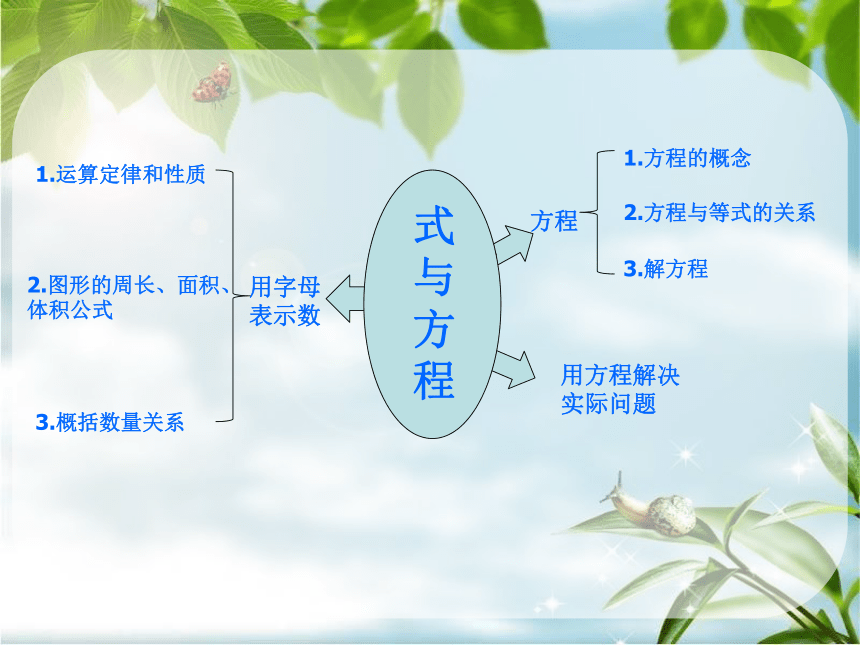
1
式
与
方
程
用字母
表示数
1.运算定律和性质
2.图形的周长、面积、体积公式
3.概括数量关系
方程
1.方程的概念
2.方程与等式的关系
3.解方程
用方程解决
实际问题
加法交换律:a+b=b+a
加法结合律:a+(b+c)=(a+b)+c
乘法交换律:ab=ba
乘法结合律:a(bc)=(ab)c
乘法分配律:a(b+c)=ab+ac
用字母表示运算定律和性质
减法的性质:a-b-c=a-(b+c)
除法的性质:a÷b÷c=a÷(b×c)
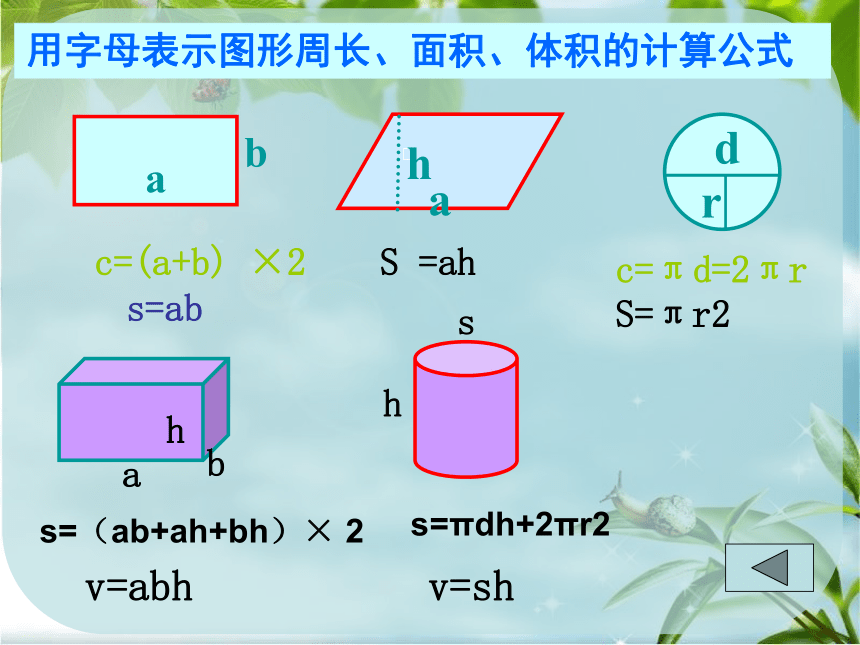
1.字母表示数
a
b
a
h
S
=ah
s=ab
c=πd=2πr
S=πr2
c=(a+b)
×2
d
r
用字母表示图形周长、面积、体积的计算公式
a
b
h
h
s
v=abh
v=sh
s=(ab+ah+bh)×
2
s=πdh+2πr2
用字母表示数可以简明地表示数量关系
例如:
1.用s表示路程,v表示速度,t表示时间,那么
2.每人栽种5棵树,a人一共栽
5a
棵树。
思考:含有字母的式子,在书写时需要注意什么?
路程
=速度×时间
s=
vt
用含有字母的式子表示下面的数量
学以致用
(1)一种贺卡的单价是
a
元,小张买5张这样的贺卡,用去(
)元;小明买n张这样的贺
卡,付出10元,应找回(
)元。
5a
10-an
(2)苹果的单价是6.2元/千克,梨的单价是4.5元/千克。妈妈买了a千克苹果和b千克梨,一共要付(
)元。
6.2a+4.5b
(3)一个正方形的边长是a米,周长是(
)米,面积是(
)平方米。当a=3时,正方形的周长是(
)米,面积是(
)平方米。
4a
a
2
12
9
3m
m-2
m+2
(4)m
表示一个偶数,与他相邻的两个偶
数是(
)和(
),这三个数的和是
(
)。
(m-2)+m+(m+2)=3m
学校买来9个足球,每个ɑ元,又买来b个篮球,每个58元。
9
ɑ表示
58
b表示
58-
ɑ表示
9
ɑ+
58
b表示
9个足球的总价
b个篮球的总价
篮球的单价比足球的单价贵多少钱
学校买足球和篮球的总价钱
9×45+58×6=753
如果ɑ
=
45
,
b
=
6
则9
ɑ+
58
b=
每人栽种5棵树,a人一共栽5a棵树。
5a=100
2.认识方程解方程
思考:如果一共栽了100棵树,我们
可以列出怎样的等式?
方程及相关概念
方程
:
等式
方程与等式的关系:
含有未知数的等式叫方程。
如:4x+5不是方程,X=5是方程
方程一定是等式,但等式不一定是方程。
方程
判断下列式子哪些是方程,为什么?
X-0.25=
X+8
2×6+10=22
X
=
0
3x+5>20
=
30%
√
√
√
×
×
×
解方程:
解方程的依据是什么?
等式的性质:
1、等式的两边同时加上(或减去)同一个数,等式仍然成立。
2、等式的两边同时乘(或除以)同一个数(0除外),等式仍然成立。
解:16
+
4X
-
16
=
40
-
16
4X
=
24
4X
÷
4
=
24
÷
4
X
=
6
解方程:
方程的解:
使方程左右两边相等的未知数的值。
解方程:
求方程解的过程叫解方程。
思考:
你是如何进行检验的?
开通前套数×5
—
4
=
现在收看的套数
解:设开通有线电视前能收看x套节目。
5x-4=56
答:开通有线电视前能收看12套节目。
3.用方程解决实际问题
5x=60
X=12
甲的路程
+
乙的路程
=
总路程
走进生活
长江三峡水库总库容
–
刘家峡水库=336亿立方米
(1)根据题意,设谁为未知数x。
(2)找出具体的数量,列出等量关系式。
(3)根据等量关系式,列出方程。
(4)解方程
(5)检验并答。
列方程解应用题的步骤
课堂小结:
本节课你有什么收获?
式
与
方
程
用字母
表示数
1.运算定律和性质
2.图形的周长、面积、
体积公式
3.概括数量关系
方程
1.方程的概念
2.方程与等式的关系
3.解方程
用方程解决
实际问题
作业:
课本82页第4题、第7题
总复习:式与方程
苏教版六年级数学下册
1
式
与
方
程
用字母
表示数
1.运算定律和性质
2.图形的周长、面积、体积公式
3.概括数量关系
方程
1.方程的概念
2.方程与等式的关系
3.解方程
用方程解决
实际问题
加法交换律:a+b=b+a
加法结合律:a+(b+c)=(a+b)+c
乘法交换律:ab=ba
乘法结合律:a(bc)=(ab)c
乘法分配律:a(b+c)=ab+ac
用字母表示运算定律和性质
减法的性质:a-b-c=a-(b+c)
除法的性质:a÷b÷c=a÷(b×c)
1.字母表示数
a
b
a
h
S
=ah
s=ab
c=πd=2πr
S=πr2
c=(a+b)
×2
d
r
用字母表示图形周长、面积、体积的计算公式
a
b
h
h
s
v=abh
v=sh
s=(ab+ah+bh)×
2
s=πdh+2πr2
用字母表示数可以简明地表示数量关系
例如:
1.用s表示路程,v表示速度,t表示时间,那么
2.每人栽种5棵树,a人一共栽
5a
棵树。
思考:含有字母的式子,在书写时需要注意什么?
路程
=速度×时间
s=
vt
用含有字母的式子表示下面的数量
学以致用
(1)一种贺卡的单价是
a
元,小张买5张这样的贺卡,用去(
)元;小明买n张这样的贺
卡,付出10元,应找回(
)元。
5a
10-an
(2)苹果的单价是6.2元/千克,梨的单价是4.5元/千克。妈妈买了a千克苹果和b千克梨,一共要付(
)元。
6.2a+4.5b
(3)一个正方形的边长是a米,周长是(
)米,面积是(
)平方米。当a=3时,正方形的周长是(
)米,面积是(
)平方米。
4a
a
2
12
9
3m
m-2
m+2
(4)m
表示一个偶数,与他相邻的两个偶
数是(
)和(
),这三个数的和是
(
)。
(m-2)+m+(m+2)=3m
学校买来9个足球,每个ɑ元,又买来b个篮球,每个58元。
9
ɑ表示
58
b表示
58-
ɑ表示
9
ɑ+
58
b表示
9个足球的总价
b个篮球的总价
篮球的单价比足球的单价贵多少钱
学校买足球和篮球的总价钱
9×45+58×6=753
如果ɑ
=
45
,
b
=
6
则9
ɑ+
58
b=
每人栽种5棵树,a人一共栽5a棵树。
5a=100
2.认识方程解方程
思考:如果一共栽了100棵树,我们
可以列出怎样的等式?
方程及相关概念
方程
:
等式
方程与等式的关系:
含有未知数的等式叫方程。
如:4x+5不是方程,X=5是方程
方程一定是等式,但等式不一定是方程。
方程
判断下列式子哪些是方程,为什么?
X-0.25=
X+8
2×6+10=22
X
=
0
3x+5>20
=
30%
√
√
√
×
×
×
解方程:
解方程的依据是什么?
等式的性质:
1、等式的两边同时加上(或减去)同一个数,等式仍然成立。
2、等式的两边同时乘(或除以)同一个数(0除外),等式仍然成立。
解:16
+
4X
-
16
=
40
-
16
4X
=
24
4X
÷
4
=
24
÷
4
X
=
6
解方程:
方程的解:
使方程左右两边相等的未知数的值。
解方程:
求方程解的过程叫解方程。
思考:
你是如何进行检验的?
开通前套数×5
—
4
=
现在收看的套数
解:设开通有线电视前能收看x套节目。
5x-4=56
答:开通有线电视前能收看12套节目。
3.用方程解决实际问题
5x=60
X=12
甲的路程
+
乙的路程
=
总路程
走进生活
长江三峡水库总库容
–
刘家峡水库=336亿立方米
(1)根据题意,设谁为未知数x。
(2)找出具体的数量,列出等量关系式。
(3)根据等量关系式,列出方程。
(4)解方程
(5)检验并答。
列方程解应用题的步骤
课堂小结:
本节课你有什么收获?
式
与
方
程
用字母
表示数
1.运算定律和性质
2.图形的周长、面积、
体积公式
3.概括数量关系
方程
1.方程的概念
2.方程与等式的关系
3.解方程
用方程解决
实际问题
作业:
课本82页第4题、第7题
