18.2.2 菱形的判定课件(17张PPT)
文档属性
| 名称 | 18.2.2 菱形的判定课件(17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 123.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-29 17:11:01 | ||
图片预览

文档简介
菱形的判定
温故知新:
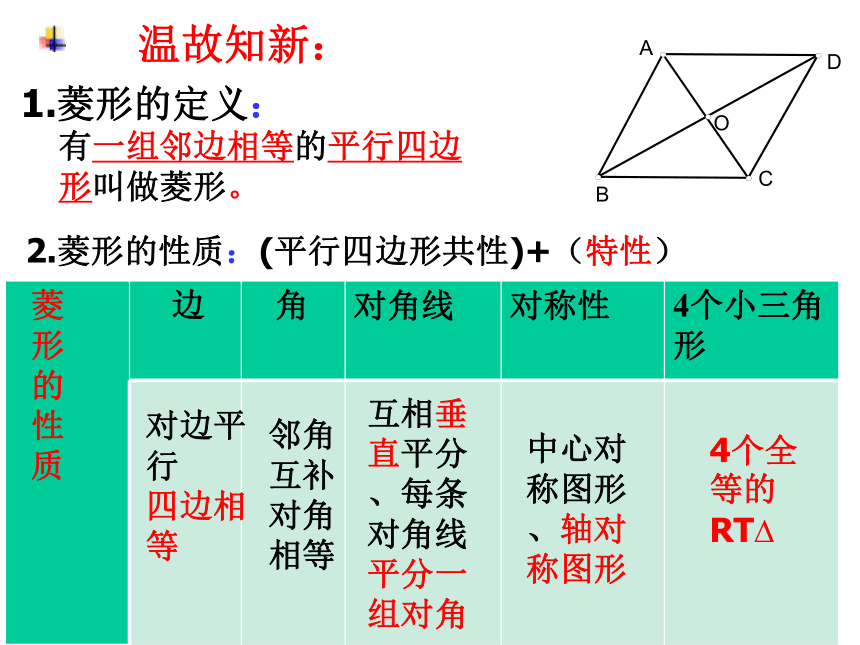
1.菱形的定义:
2.菱形的性质:(平行四边形共性)+(特性)
有一组邻边相等的平行四边形叫做菱形。
?
?
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 菱
形
的
性
质
边
角
对角线
对称性
4个小三角形
对边平行
四边相等
邻角互补对角相等
互相垂直平分、每条对角线平分一组对角
中心对称图形、轴对称图形
4个全等的RT?
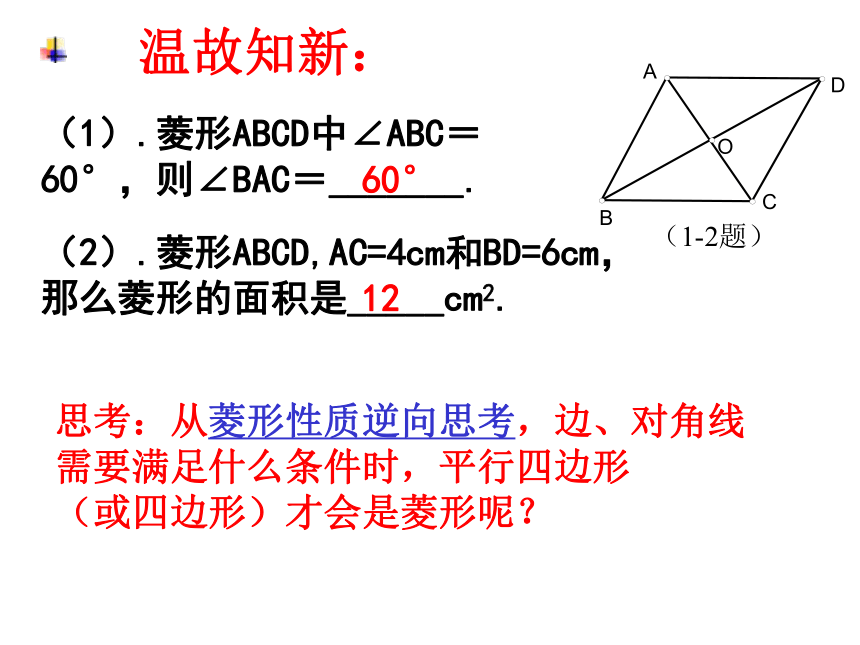
(1).菱形ABCD中∠ABC=60°,则∠BAC=_______.
60°
(2).菱形ABCD,AC=4cm和BD=6cm,那么菱形的面积是_____cm2.
12
温故知新:
(1-2题)
思考:从菱形性质逆向思考,边、对角线
需要满足什么条件时,平行四边形
(或四边形)才会是菱形呢?
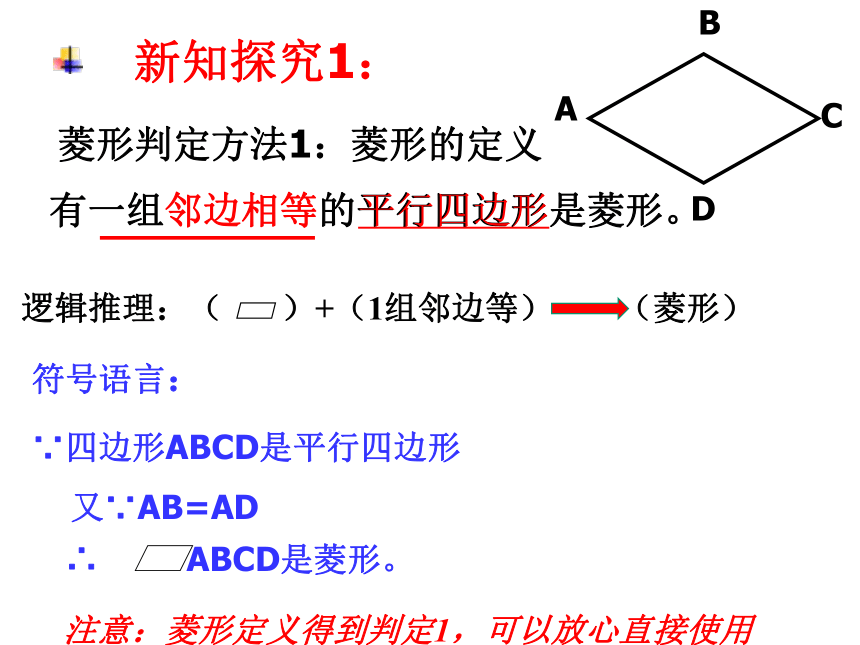
新知探究1:
菱形判定方法1:菱形的定义
有一组邻边相等的平行四边形是菱形。
平行四边形
符号语言:
∵四边形ABCD是平行四边形
又∵AB=AD
∴ ABCD是菱形。
A
B
C
D
注意:菱形定义得到判定1,可以放心直接使用
逻辑推理:( )+(1组邻边等) (菱形)
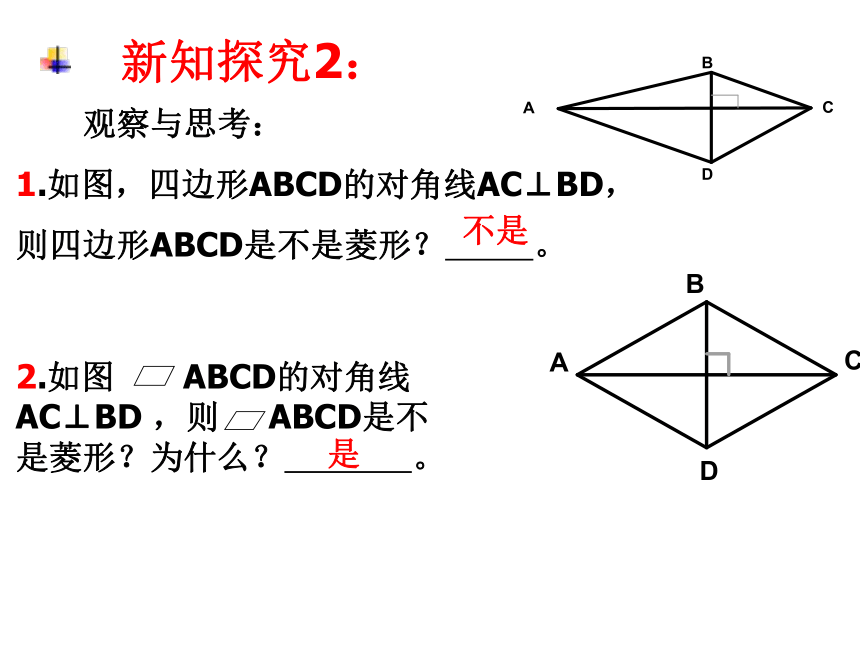
观察与思考:
1.如图,四边形ABCD的对角线AC⊥BD,
则四边形ABCD是不是菱形? 。
2.如图 ABCD的对角线AC⊥BD ,则 ABCD是不是菱形?为什么? 。
新知探究2:
不是
是
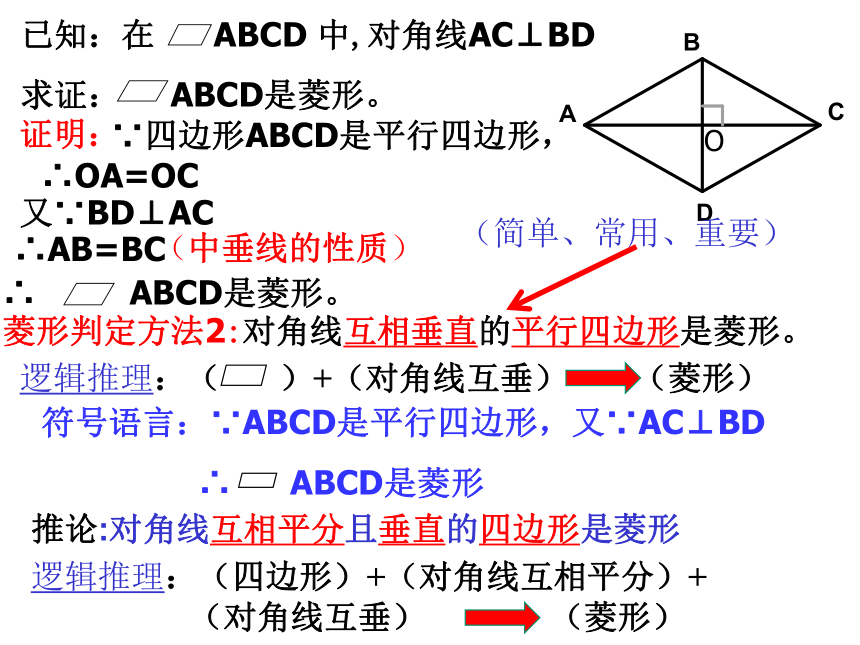
已知:在 ABCD 中,对角线AC⊥BD
求证: ABCD是菱形。
证明:
∵四边形ABCD是平行四边形,
∴OA=OC
又∵BD⊥AC
∴ ABCD是菱形。
∴AB=BC
菱形判定方法2:对角线互相垂直的平行四边形是菱形。
O
(中垂线的性质)
推论:对角线互相平分且垂直的四边形是菱形
符号语言:∵ABCD是平行四边形,又∵AC⊥BD
∴ ABCD是菱形
逻辑推理:( )+(对角线互垂) (菱形)
逻辑推理:(四边形)+(对角线互相平分)+
(对角线互垂) (菱形)
(简单、常用、重要)
A
B
C
D
O
A
B
C
D
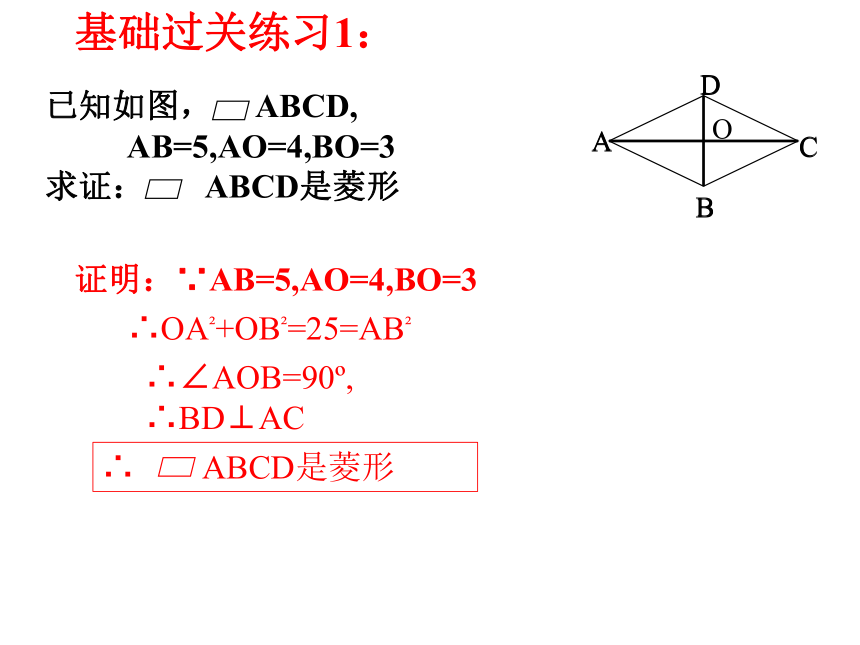
已知如图, ABCD,
AB=5,AO=4,BO=3
求证: ABCD是菱形
证明:∵AB=5,AO=4,BO=3
∴OA?+OB?=25=AB?
∴∠AOB=90?,
∴BD⊥AC
∴ ABCD是菱形
基础过关练习1:
已知:四边形ABCD中,AB=BC=CD=DA
求证:四边形ABCD是菱形。
菱形判定方法3:四条边相等的四边形是菱形。
∵AB=BC=CD=DA
∴四边形ABCD是菱形。
符号语言:
A
B
C
D
新知探究3:
证明:
∴四边形ABCD是平行四边形。
∵AB=CD,AD=BC,
又∵AB=BC,
∴四边形ABCD是菱形。
逻辑推理:(四边形)+(四边相等) (菱形)
(简单、常用、重要)
及时梳理
菱形的判定方法:
判定(1)( )+( )
判定(2)( )+( )
判定(3)(四边形)+( )
推论:(四边形)+( )
+( )
1组邻边等
对角线互垂
4条边等
对角线互相平分
对角线互相垂直
菱形
菱形
菱形
菱形
1.如图请添加一个条 使
ABCD 是菱形.
基础过关练习2:
AB=AD
或AC⊥BD
A
B
C
D
1
2
3
2.已知如图, ABCD中,
∠1=∠2,ABCD的形状 ,理由:
菱形
证明:∵ABCD是平行四边形
∴AD ∥ BC
∴∠1=∠3
∴∠2=∠3
又∵∠1=∠2
∴ ABCD是菱形
∴AB=CB
1.已知:如图 ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F.
求证:四边形AFCE是菱形.
3
4
(2)证明菱形的思路:
思路①先证明( ),再证明( )
思路②直接证明( )
(1)读小条件 想 一些小结论
ABCD 想到 哪些小结论
EF垂直平分AC 想到 哪些小结论
(3)要证明AFCE是平行四边形,就需要
先证明( ),那就容易想到
证明( )
平行四边形
1组邻边等或对角线互垂
四边都等
AE=CF或者OE=OF
△AOE≌△COF
小试牛刀
1.已知:如图 ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F.
求证:四边形AFCE是菱形.
证明:∵ 四边形ABCD是平行四边形,
∴ AE∥FC.
∴∠1=∠2.∠3=∠4
∴AAS可证△AOE≌△COF.
∴EO=FO.
∴AFCE是平行四边形.
又EF⊥AC,
又EF垂直平分AC,
∴ AFCE是菱形
∵ AO=CO,
3
4
∴AO=CO,
思考:
1.证△AOE≌△COF还有方法吗?
2.证AFCE是平行四边形还有方法吗?
3.证AFCE是菱形还有方法吗?
1.已知:如图 ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F.
求证:AFCE是菱形.
AE∥CF(易证)
AE=CF(理由)
证△AOE≌△COF.
∴EO=FO(理由)
一条菱特( 易证 )
证AFCE是平行四边形( 理由 )
∵ AO=CO(易证)
3
4
证△AOE≌△COF
AAS或ASA
AAS或ASA
四边相等
△AOE≌△COF
得AE=CF
EF垂直、平分AC
得EA=EC,FA=FC
课堂收获:
(一)菱形判定定理
判定1:
判定2:
判定3:
推论:
(二)大题中证明菱形的思路方法
1.先证明是(平行四边形),再证明
有( )
2.直接证明( )
有一组邻边相等的平行四边形是菱形。
对角线互相垂直的平行四边形是菱形。
对角线互相平分且垂直的四边形是菱形
四条边相等的四边形是菱形。
一条菱形特性
四边相等
注意:(平行四边形)可以用5种说法替换,所以菱形判定有十多种变式说法
已知:如图,在四边形 ABCD 中,点 E、F 分别是线段 AD、BC 的中点,G、H 分别是线段 BD、AC 的中点,
(1)求证:四边形 EGFH 是平行四边
(2)ABCD的边满足什么条件时,EGFH为菱形,说明理由
拓展提升
一组对边平行且相等
两组对边分别相等
两组对边分别平行
思路分析:
(1)从中位线角度你有几种方法证明到EGFH是平行四形? ; ;
. (2)从执果索因角度,逆向分析ABCD 的边满足什么条件? , EGFH才变成菱形。
已知:如图,在四边形 ABCD 中,点 E、F 分别是线段 AD、BC 的中点,G、H 分别是线段 BD、AC 的中点,
(1)求证:四边形 EGFH 是平行四边
(2)ABCD的边满足什么条件时,EGFH为菱形,说明理由
拓展提升
(2)求证:EGFH是菱形
EGFH是平行四边形(已证)
EG=EH (交代理由)
∴EGFH是平行四边形
∴EG FH
证明:∵E、G、F、H分别
是…的中点
作业:
1.教材第60页6题
2.拓展提升
3. 如图,已知 E、F、G、H 分别是矩形ABCD四边 AB、BC、CD、DA 的中点,且四边形 EFGH 的周长为 16cm,求矩形 ABCD 的对角线长
O
温故知新:
1.菱形的定义:
2.菱形的性质:(平行四边形共性)+(特性)
有一组邻边相等的平行四边形叫做菱形。
?
?
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 菱
形
的
性
质
边
角
对角线
对称性
4个小三角形
对边平行
四边相等
邻角互补对角相等
互相垂直平分、每条对角线平分一组对角
中心对称图形、轴对称图形
4个全等的RT?
(1).菱形ABCD中∠ABC=60°,则∠BAC=_______.
60°
(2).菱形ABCD,AC=4cm和BD=6cm,那么菱形的面积是_____cm2.
12
温故知新:
(1-2题)
思考:从菱形性质逆向思考,边、对角线
需要满足什么条件时,平行四边形
(或四边形)才会是菱形呢?
新知探究1:
菱形判定方法1:菱形的定义
有一组邻边相等的平行四边形是菱形。
平行四边形
符号语言:
∵四边形ABCD是平行四边形
又∵AB=AD
∴ ABCD是菱形。
A
B
C
D
注意:菱形定义得到判定1,可以放心直接使用
逻辑推理:( )+(1组邻边等) (菱形)
观察与思考:
1.如图,四边形ABCD的对角线AC⊥BD,
则四边形ABCD是不是菱形? 。
2.如图 ABCD的对角线AC⊥BD ,则 ABCD是不是菱形?为什么? 。
新知探究2:
不是
是
已知:在 ABCD 中,对角线AC⊥BD
求证: ABCD是菱形。
证明:
∵四边形ABCD是平行四边形,
∴OA=OC
又∵BD⊥AC
∴ ABCD是菱形。
∴AB=BC
菱形判定方法2:对角线互相垂直的平行四边形是菱形。
O
(中垂线的性质)
推论:对角线互相平分且垂直的四边形是菱形
符号语言:∵ABCD是平行四边形,又∵AC⊥BD
∴ ABCD是菱形
逻辑推理:( )+(对角线互垂) (菱形)
逻辑推理:(四边形)+(对角线互相平分)+
(对角线互垂) (菱形)
(简单、常用、重要)
A
B
C
D
O
A
B
C
D
已知如图, ABCD,
AB=5,AO=4,BO=3
求证: ABCD是菱形
证明:∵AB=5,AO=4,BO=3
∴OA?+OB?=25=AB?
∴∠AOB=90?,
∴BD⊥AC
∴ ABCD是菱形
基础过关练习1:
已知:四边形ABCD中,AB=BC=CD=DA
求证:四边形ABCD是菱形。
菱形判定方法3:四条边相等的四边形是菱形。
∵AB=BC=CD=DA
∴四边形ABCD是菱形。
符号语言:
A
B
C
D
新知探究3:
证明:
∴四边形ABCD是平行四边形。
∵AB=CD,AD=BC,
又∵AB=BC,
∴四边形ABCD是菱形。
逻辑推理:(四边形)+(四边相等) (菱形)
(简单、常用、重要)
及时梳理
菱形的判定方法:
判定(1)( )+( )
判定(2)( )+( )
判定(3)(四边形)+( )
推论:(四边形)+( )
+( )
1组邻边等
对角线互垂
4条边等
对角线互相平分
对角线互相垂直
菱形
菱形
菱形
菱形
1.如图请添加一个条 使
ABCD 是菱形.
基础过关练习2:
AB=AD
或AC⊥BD
A
B
C
D
1
2
3
2.已知如图, ABCD中,
∠1=∠2,ABCD的形状 ,理由:
菱形
证明:∵ABCD是平行四边形
∴AD ∥ BC
∴∠1=∠3
∴∠2=∠3
又∵∠1=∠2
∴ ABCD是菱形
∴AB=CB
1.已知:如图 ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F.
求证:四边形AFCE是菱形.
3
4
(2)证明菱形的思路:
思路①先证明( ),再证明( )
思路②直接证明( )
(1)读小条件 想 一些小结论
ABCD 想到 哪些小结论
EF垂直平分AC 想到 哪些小结论
(3)要证明AFCE是平行四边形,就需要
先证明( ),那就容易想到
证明( )
平行四边形
1组邻边等或对角线互垂
四边都等
AE=CF或者OE=OF
△AOE≌△COF
小试牛刀
1.已知:如图 ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F.
求证:四边形AFCE是菱形.
证明:∵ 四边形ABCD是平行四边形,
∴ AE∥FC.
∴∠1=∠2.∠3=∠4
∴AAS可证△AOE≌△COF.
∴EO=FO.
∴AFCE是平行四边形.
又EF⊥AC,
又EF垂直平分AC,
∴ AFCE是菱形
∵ AO=CO,
3
4
∴AO=CO,
思考:
1.证△AOE≌△COF还有方法吗?
2.证AFCE是平行四边形还有方法吗?
3.证AFCE是菱形还有方法吗?
1.已知:如图 ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F.
求证:AFCE是菱形.
AE∥CF(易证)
AE=CF(理由)
证△AOE≌△COF.
∴EO=FO(理由)
一条菱特( 易证 )
证AFCE是平行四边形( 理由 )
∵ AO=CO(易证)
3
4
证△AOE≌△COF
AAS或ASA
AAS或ASA
四边相等
△AOE≌△COF
得AE=CF
EF垂直、平分AC
得EA=EC,FA=FC
课堂收获:
(一)菱形判定定理
判定1:
判定2:
判定3:
推论:
(二)大题中证明菱形的思路方法
1.先证明是(平行四边形),再证明
有( )
2.直接证明( )
有一组邻边相等的平行四边形是菱形。
对角线互相垂直的平行四边形是菱形。
对角线互相平分且垂直的四边形是菱形
四条边相等的四边形是菱形。
一条菱形特性
四边相等
注意:(平行四边形)可以用5种说法替换,所以菱形判定有十多种变式说法
已知:如图,在四边形 ABCD 中,点 E、F 分别是线段 AD、BC 的中点,G、H 分别是线段 BD、AC 的中点,
(1)求证:四边形 EGFH 是平行四边
(2)ABCD的边满足什么条件时,EGFH为菱形,说明理由
拓展提升
一组对边平行且相等
两组对边分别相等
两组对边分别平行
思路分析:
(1)从中位线角度你有几种方法证明到EGFH是平行四形? ; ;
. (2)从执果索因角度,逆向分析ABCD 的边满足什么条件? , EGFH才变成菱形。
已知:如图,在四边形 ABCD 中,点 E、F 分别是线段 AD、BC 的中点,G、H 分别是线段 BD、AC 的中点,
(1)求证:四边形 EGFH 是平行四边
(2)ABCD的边满足什么条件时,EGFH为菱形,说明理由
拓展提升
(2)求证:EGFH是菱形
EGFH是平行四边形(已证)
EG=EH (交代理由)
∴EGFH是平行四边形
∴EG FH
证明:∵E、G、F、H分别
是…的中点
作业:
1.教材第60页6题
2.拓展提升
3. 如图,已知 E、F、G、H 分别是矩形ABCD四边 AB、BC、CD、DA 的中点,且四边形 EFGH 的周长为 16cm,求矩形 ABCD 的对角线长
O
