第1章三角形的证明 单元培优测试卷(Word版 含答案)
文档属性
| 名称 | 第1章三角形的证明 单元培优测试卷(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 642.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-28 20:29:46 | ||
图片预览

文档简介
第1章三角形的证明 单元培优测试卷
一、选择题
1、等腰三角形中有一个角为100°,则其底角为( )
A.50° B.40° C.40°或100° D.50°或100°
2、已知等腰三角形有一边长为5,一边长为2,则其周长为( )
A.12 B.9 C.10 D.12或9
3、如图,在Rt△ABC中,∠C=90°,∠B=30°,CD是斜边AB上的高,AD=3cm,则AB的长度是( )
A.3cm B.6cm C.9cm D.12cm
4、如图,点D在△ABC的边BC上,且BC=BD+AD,则点D在( )的垂直平分线上.
A.AB B.AC C.BC D.不能确定
5、如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是( )
A.ED=CD B.∠DAC=∠B C.∠C>2∠B D.∠B+∠ADE=90°
6、如图,已知△ABC的周长是18cm,∠ABC和∠ACB的角平分线交于点O,OD⊥BC于点D,若OD=3cm,则△ABC的面积是( )cm2.
A.24 B.27 C.30 D.33
7、如图,BM是∠ABC的平分线,点D是BM上一点,点P为直线BC上的一个动点.若△ABD的面积为9,AB=6,则线段DP的长不可能是( )
A.2 B.3 C.4 D.5.5
8、如图所示,在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P,BE=BC,PG∥AD交BC于F,交AB于G,连接CP.下列结论:①∠ACB=2∠APB;②S△PAC:S△PAB=PC:PB;③BP垂直平分CE;④∠PCF=∠CPF.其中正确的有( )
A.①②④ B.①③④ C.②③④ D.①③
9、如图,AD平分∠BAC,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF.
则下列结论中:①AD是△ABC的高;②AD是△ABC的中线;③ED=FD;④AB=AE+BF.
其中正确的个数有( )
A.4个 B.3个 C.2个 D.1个
10、如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则B6B7的边长为( )
A.6 B.12 C.32 D.64
二、填空题
11、在△ABC中,AB=AC,∠A=40°,则∠B的度数为 °.
12、Rt△ABC中,∠C=90°,点D是斜边AB的中点,若CD=2,则AB= .
13、如图,在平面直角坐标系中,△ABO是边长为2的等边三角形,则A点的坐标是 .
14、如图,线段AB、BC的垂直平分线l1、l2相交于点O,若∠AOC=90°,∠A=13°,则∠C= °.
15、如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,DF⊥AC于点F,S△ABC=7,DE=2,AB=4,则AC长是 .
16、如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于E点,∠B=50°,∠FAE=20°,
则∠C= 度.
17、如图,在△ABC中,∠B=∠C,D,E分别是线段BC、AC上的一点,且AD=AE.
用等式表示∠1和∠2之间的数量关系是 .
18、如图所示,在△ABC中,∠C=90°,DE垂直平分AB,交BC于点E,垂足为点D,BE=8,∠B=15°,则EC的长为 .
19、如图,已知△ABC中高AD恰好平分边BC,∠B=30°,点P是BA延长线上一点,点
O是线段AD上一点且OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP.其中正确的为 .(填序号)
20、如图,四边形ABCD中,对角线AC、BD相交于点E,若∠ABD=∠ADC=90°,AC平分∠DAB,DE=4,BC=,则AE的长为 .
三、解答题
21、已知△ABC中,D为边BC上一点,AB=AD=CD.
(1)试说明∠ABC=2∠C;
(2)过点B作AD的平行线交CA的延长线于点E,若AD平分∠BAC,求证:AE=AB.
22、如图,在Rt△ABC中,∠C=90°,AC=6,AB=10,DE垂直平分AB,分别交AB、BC于点D、E.求CE的长.
23、已知:如图,在等腰三角形ADC中,AD=CD,且AB∥DC,CB⊥AB于B,CE⊥AD交AD的延长线于E.
(1)求证:CE=CB;
(2)如果连接BE,请写出BE与AC的关系并证明.
24、如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠BAD= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状也在改变,判断当∠BDA等于多少度时,△ADE是等腰三角形.
25、如图,在△ABC中,BM⊥AC,垂足为M.N为AB上的一点,D为BC的中点,DN=BC.
(1)求证CN⊥AB.
(2)若∠A=55°,则∠MDN= °.
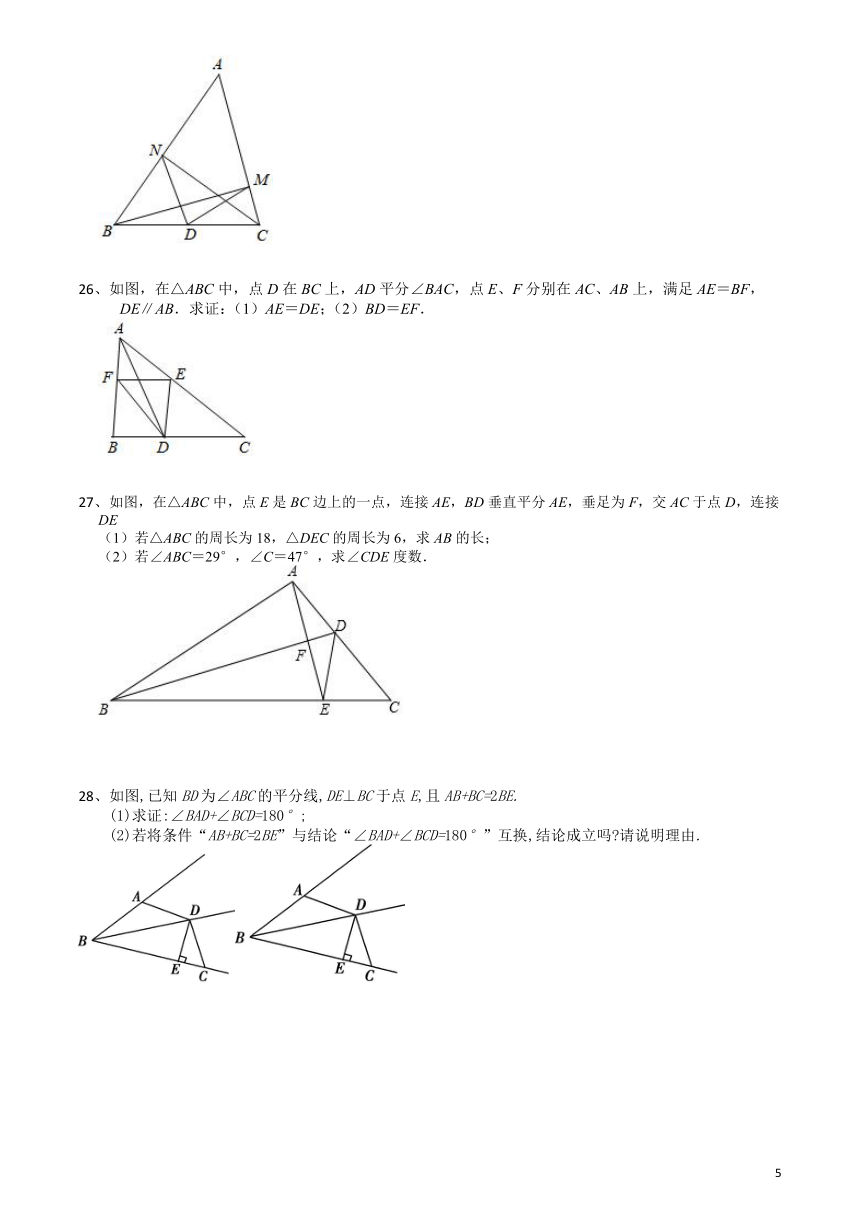
26、如图,在△ABC中,点D在BC上,AD平分∠BAC,点E、F分别在AC、AB上,满足AE=BF,
DE∥AB.求证:(1)AE=DE;(2)BD=EF.
27、如图,在△ABC中,点E是BC边上的一点,连接AE,BD垂直平分AE,垂足为F,交AC于点D,连接DE
(1)若△ABC的周长为18,△DEC的周长为6,求AB的长;
(2)若∠ABC=29°,∠C=47°,求∠CDE度数.
28、如图,已知BD为∠ABC的平分线,DE⊥BC于点E,且AB+BC=2BE.
(1)求证:∠BAD+∠BCD=180°;
(2)若将条件“AB+BC=2BE”与结论“∠BAD+∠BCD=180°”互换,结论成立吗?请说明理由.
(答案)
一、选择题
1、等腰三角形中有一个角为100°,则其底角为( )
A.50° B.40° C.40°或100° D.50°或100°
解:∵等腰三角形的一个角100°,∴100°的角是顶角,
∴底角是×(180°﹣100°)=40°,故选:B.
2、已知等腰三角形有一边长为5,一边长为2,则其周长为( )
A.12 B.9 C.10 D.12或9
解:①若5为腰长,2为底边长,
∵5,5,2能组成三角形,∴此时周长为:5+5+2=12;
②若2为腰长,5为底边长,
∵2+2=4<5,∴不能组成三角形,故舍去;
∴周长为12. 故选:A.
3、如图,在Rt△ABC中,∠C=90°,∠B=30°,CD是斜边AB上的高,AD=3cm,则AB的长度是( )
A.3cm B.6cm C.9cm D.12cm
解:在Rt△ABC中,
∵CD是斜边AB上的高,∴∠ADC=90°,∴∠ACD=∠B=30°(同角的余角相等),
∵AD=3cm,在Rt△ACD中,AC=2AD=6cm,
在Rt△ABC中,AB=2AC=12cm.∴AB的长度是12cm.故选:D.
4、如图,点D在△ABC的边BC上,且BC=BD+AD,则点D在( )的垂直平分线上.
A.AB B.AC C.BC D.不能确定
解:∵BC=BD+AD=BD+CD∴AD=CD
∴点D在AC的垂直平分线上.故选:B.
5、如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是( )
A.ED=CD B.∠DAC=∠B C.∠C>2∠B D.∠B+∠ADE=90°
解:∵DE是线段AB的垂直平分线,∴AD=BD.
∴∠B=∠BAD,∠ADE=∠BDE.∴∠B+∠ADE=90°
其它选项无法证明其是正确的.
故选:D.
6、如图,已知△ABC的周长是18cm,∠ABC和∠ACB的角平分线交于点O,OD⊥BC于点D,若OD=3cm,则△ABC的面积是( )cm2.
A.24 B.27 C.30 D.33
解:过O点作OE⊥AB于E,OF⊥AC于F,连接OA,如图,
∵OB平分∠ABC,OD⊥BC,OE⊥AB,∴OE=OD=3,
同理可得OF=OD=3,
∴S△ABC=S△OAB+S△OBC+S△OAC=×OE×AB+×OD×BC+×OF×AC=(AB+BC+AC),
∵△ABC的周长是18,∴S△ABC=×18=27(cm2).
故选:B.
7、如图,BM是∠ABC的平分线,点D是BM上一点,点P为直线BC上的一个动点.若△ABD的面积为9,AB=6,则线段DP的长不可能是( )
A.2 B.3 C.4 D.5.5
解:过点D作DE⊥AB于E,DF⊥BC于F,
∵△ABD的面积为9,AB=6,∴DE=,
∵BM是∠ABC的平分线,∴DE=3,∴DP≥3,故选:A.
8、如图所示,在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P,BE=BC,PG∥AD交BC于F,交AB于G,连接CP.下列结论:①∠ACB=2∠APB;②S△PAC:S△PAB=PC:PB;③BP垂直平分CE;④∠PCF=∠CPF.其中正确的有( )
A.①②④ B.①③④ C.②③④ D.①③
解:∵PA平分∠CAB,PB平分∠CBE,∴∠PAB=∠CAB,∠PBE=∠CBE,
∵∠CBE=∠CAB+∠ACB,∠PBE=∠PAB+∠APB,∴∠ACB=2∠APB;故①正确;
过P作PM⊥AB于M,PN⊥AC于N,PS⊥BC于S,∴PM=PN=PS,∴PC平分∠BCD,
∵S△PAC:S△PAB=(AC?PN):(AB?PM)=AC:AB;故②不正确;
∵BE=BC,BP平分∠CBE∴BP垂直平分CE(三线合一),故③正确;
∵PG∥AD,∴∠FPC=∠DCP
∵PC平分∠DCB,∴∠DCP=∠PCF,∴∠PCF=∠CPF,故④正确.
本题正确的有:①③④
故选:B.
9、如图,AD平分∠BAC,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF.
则下列结论中:①AD是△ABC的高;②AD是△ABC的中线;③ED=FD;④AB=AE+BF.
其中正确的个数有( )
A.4个 B.3个 C.2个 D.1个
解:∵BC恰好平分∠ABF,∴∠ABC=∠FBD,
∵AC∥BF,∴∠C=∠FBD,∴∠C=∠ABC,∴△ABC为等腰三角形,
∵AD平分∠BAC,∴AD⊥BC,CD=BD,所以①②正确;
过D点作DH⊥AB于H,如图,
∵AD平分∠BAC,DE⊥AC,DH⊥AB,∴DE=DH,
∵AC∥BF,DE⊥AC,∴DF⊥BF,
∵BD平分∠ABF,DH⊥AB,∴DH=DF,∴DE=DF,所以③正确;
在△ADE和△ADH中,,∴△ADE≌△ADH(HL),∴AH=AE,
同理可得BH=BF,∴AB=AH+BH=AE+BF,所以④正确.
故选:A.
10、如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则B6B7的边长为( )
A.6 B.12 C.32 D.64
解:∵△A1B1A2是等边三角形,∴A1B1=A2B1,∠3=∠4=∠12=60°,∴∠2=120°,
∵∠MON=30°,∴∠1=180°﹣120°﹣30°=30°,
又∵∠3=60°,∴∠5=180°﹣60°﹣30°=90°,
∵∠MON=∠1=30°,∴OA1=A1B1=1,∴A2B1=1,
∵△A2B2A3、△A3B3A4是等边三角形,∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,∴A2B2=2B1A2=2,B3A3=2B2A3,
∴A3B3=4B1A2=4,A4B4=8B1A2=8,A5B5=16B1A2=16,
以此类推:A7B7=26B1A2=26=64,B6A7==32,△B7B6A7是直角三角形,∠B7B6A7=90°,
∴B6B7===32.
故选:C.
二、填空题
11、在△ABC中,AB=AC,∠A=40°,则∠B的度数为 °.
解:∵AB=AC,∴∠B=∠C,
∵∠A=40°,∴∠B=(180°﹣40°)÷2=70°.故答案为:70.
12、Rt△ABC中,∠C=90°,点D是斜边AB的中点,若CD=2,则AB= .
解:在Rt△ABC中,点D是斜边AB的中点,CD=2,
∴AB=2CD=2×2=4,
故答案为:4.
13、如图,在平面直角坐标系中,△ABO是边长为2的等边三角形,则A点的坐标是 .
解:过A作AE⊥x轴于E,
∵△ABO是等边三角形,边长为2,∴OA=2,OE=BE=1,
在Rt△AEO中,由勾股定理得:AE===,
即点A的坐标为(1,﹣).故答案为:(1,﹣).
14、如图,线段AB、BC的垂直平分线l1、l2相交于点O,若∠AOC=90°,∠A=13°,则∠C= °.
解:如图,连接OB,
∵OD垂直平分AB,∴OA=OB,∴∠ABO=∠A=13°,
∴∠AOB=180°﹣13°﹣13°=154°,
∵∠AOB+∠BOC+∠AOC=360°,∴∠BOC=360°﹣90°﹣154°=116°,
∵OE垂直平分BC,∴∠C=∠OBC=(180°﹣116°)=32°.
故答案为:32.
15、如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,DF⊥AC于点F,S△ABC=7,DE=2,AB=4,则AC长是 .
解:∵AD是△ABC中∠BAC的角平分线,DE⊥AB,DF⊥AC,∴DE=DF,
∴S△ABC=×4×2+AC?2=7,解得AC=3. 故答案为:3.
16、如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于E点,∠B=50°,∠FAE=20°,
则∠C= 度.
解:∵DE是线段AC的垂直平分线,∴EA=EC,∴∠EAC=∠C,
∵AF平分∠BAC,
∴∠BAF=∠CAF=∠FAE+∠CAE=20°+∠C,
由三角形内角和定理得,∠B+∠BAC+∠C=180°,即50°+20°+∠C+20°+∠C+∠C=180°,
解得,∠C=30°, 故答案为:30.
17、如图,在△ABC中,∠B=∠C,D,E分别是线段BC、AC上的一点,且AD=AE.
用等式表示∠1和∠2之间的数量关系是 .
解:根据三角形外角的性质得:∠AED=∠CDE+∠C,∠ADC=∠B+∠BAD,
∵AD=AE,∴∠AED=∠ADE,
∵AB=AC,∴∠B=∠C,
∴∠B+∠BAD=∠EDC+∠C+∠CDE,即∠BAD=2∠CDE,∠1=2∠2.
故答案为:∠1=2∠2.
18、如图所示,在△ABC中,∠C=90°,DE垂直平分AB,交BC于点E,垂足为点D,BE=8,∠B=15°,则EC的长为 .
解:在△ABC中,∠ACB=90°,∠B=15°,∴∠BAC=90°﹣15°=75°,
∵DE垂直平分AB,BE=8,∴BE=AE=8,∴∠EAB=∠B=15°,
∴∠EAC=75°﹣15°=60°,
∵∠C=90°,∴∠AEC=30°,∴AC=AE=×8=4,∴EC=AC=4,
故答案为:.
19、如图,已知△ABC中高AD恰好平分边BC,∠B=30°,点P是BA延长线上一点,点
O是线段AD上一点且OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP.其中正确的为 .(填序号)
解:①连接OB,如图1,
∵△ABC中高AD恰好平分边BC,即AD是BC垂直平分线,∴AB=AC,BD=CD,
∴OB=OC=OP,∴∠APO=∠ABO,∠DBO=∠DCO,
∵∠ABC=∠ABO+∠DBO=30°,∴∠APO+∠DCO=30°.故①正确;
②△OBP中,∠BOP=180°﹣∠OPB﹣∠OBP,
△BOC中,∠BOC=180°﹣∠OBC﹣∠OCB,
∴∠POC=360°﹣∠BOP﹣∠BOC=∠OPB+∠OBP+∠OBC+∠OCB,
∵∠OPB=∠OBP,∠OBC=∠OCB,∴∠POC=2∠ABD=60°,
∵PO=OC,∴△OPC是等边三角形,故②正确;
③如图2,在AC上截取AE=PA,
∵∠PAE=180°﹣∠BAC=60°,∴△APE是等边三角形,
∴∠PEA=∠APE=60°,PE=PA,∴∠APO+∠OPE=60°,
∵∠OPE+∠CPE=∠CPO=60°,∴∠APO=∠CPE,
∵OP=CP,在△OPA和△CPE中,,∴△OPA≌△CPE(SAS),
∴AO=CE,∴AC=AE+CE=AO+AP;故③正确;
④如图3,作CH⊥BP,
∵∠HCB=60°,∠PCO=60°,∴∠PCH=∠OCD,
在△CDO和△CHP中,,∴△CDO≌△CHP(AAS),
∴S△OCD=S△CHP∴CH=CD,
∵CD=BD,∴BD=CH,
在Rt△ABD和Rt△ACH中,,∴Rt△ABD≌Rt△ACH(HL),∴S△ABD=S△AHC,
∵四边形OAPC面积=S△OAC+S△AHC+S△CHP,S△ABC=S△AOC+S△ABD+S△OCD
∴四边形OAPC面积=S△ABC.故④正确.
故答案为:①②③④.
20、如图,四边形ABCD中,对角线AC、BD相交于点E,若∠ABD=∠ADC=90°,AC平分∠DAB,DE=4,BC=,则AE的长为 .
解:过点C作CH⊥AB交AB的延长线于H,CJ⊥BD于J.
∵CA平分∠DAN,CD⊥AD,CH⊥AH,∴∠DAC=∠BAC,CD=CH,
∵∠ADC=∠ABD=90°,∴∠DAC+∠ACD=90°,∠CAB+∠AEB=90°,∴∠ACD=∠AEB,
∵∠DEC=∠AEB,∴∠DEC=∠DCE,∴DE=DC=CH=4,
∵∠CJB=∠JBH=∠H=90°,∴四边形BHCE是矩形,
∴BE=CH=4,EC=BH===,
∴DE===,
∴JE=DE﹣DJ=4﹣=,EB=BJ﹣EJ=4﹣=,
∴EC===,
∵CJ∥AB,∴=,∴=,∴AE=,
故答案为:
三、解答题
21、已知△ABC中,D为边BC上一点,AB=AD=CD.
(1)试说明∠ABC=2∠C;
(2)过点B作AD的平行线交CA的延长线于点E,若AD平分∠BAC,求证:AE=AB.
证明:(1)∵AB=AD,∴∠ABC=∠ADB,
∵AD=CD,∴∠DAC=∠C,
∵∠ADB=∠DAC+∠C=2∠C,∴∠ABC=2∠C;
(2)∵AD平分∠BAC,∴∠DAB=∠CAD,
∵BE∥AD,∴∠DAB=∠ABE,∠E=∠CAD,
∴∠ABE=∠E,∴AE=AB.
22、如图,在Rt△ABC中,∠C=90°,AC=6,AB=10,DE垂直平分AB,分别交AB、BC于点D、E.求CE的长.
解:在Rt△ABC中,∠C=90°,∴;
∵DE垂直平分AB,分别交AB、BC于点D、E,∴AE=BE;
设CE=x,则AE=BE=8﹣x;
在Rt△ACE中,∠C=90°,∴CE2+AC2=AE2;即x2+62=(8﹣x)2,
解得,即.
23、已知:如图,在等腰三角形ADC中,AD=CD,且AB∥DC,CB⊥AB于B,CE⊥AD交AD的延长线于E.
(1)求证:CE=CB;
(2)如果连接BE,请写出BE与AC的关系并证明.
证明:(1)∵AD=CD,∴∠DAC=∠DCA,
∵AB∥CD,∴∠DCA=∠CAB,
∴∠DAC=∠CAB,∴AC是∠EAB的角平分线,
∵CE⊥AE,CB⊥AB,∴CE=CB;
( 2) AC垂直平分BE,
证明:由(1)知,CE=CB,
∵CE⊥AE,CB⊥AB,∴∠CEA=∠CBA=90°,
∵在Rt△CEA和Rt△CBA中,∴Rt△CEA≌Rt△CBA(HL),
∴AE=AB,CE=CB,
∴点A、点C在线段BE的垂直平分线上,∴AC垂直平分BE.
24、如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠BAD= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状也在改变,判断当∠BDA等于多少度时,△ADE是等腰三角形.
解:(1)∠BAD=180°﹣∠ABD﹣∠BDA=180°﹣40°﹣115°=25°;
从图中可以得知,点D从B向C运动时,∠BDA逐渐变小;
故答案为:25°;小.
(2∵∠EDC+∠EDA=∠DAB+∠B,∠B=∠EDA=40°,
∴∠EDC=∠DAB.,
∵∠B=∠C,∴当DC=AB=2时,△ABD≌△DCE,
(3)∵AB=AC,∴∠B=∠C=40°,
①当AD=AE时,∠ADE=∠AED=40°,
∵∠AED>∠C,∴此时不符合;
②当DA=DE时,即∠DAE=∠DEA=(180°﹣40°)=70°,
∵∠BAC=180°﹣40°﹣40°=100°,
∴∠BAD=100°﹣70°=30°;∴∠BDA=180°﹣30°﹣40°=110°;
③当EA=ED时,∠ADE=∠DAE=40°,
∴∠BAD=100°﹣40°=60°,∴∠BDA=180°﹣60°﹣40°=80°;
∴当∠ADB=110°或80°时,△ADE是等腰三角形.
25、如图,在△ABC中,BM⊥AC,垂足为M.N为AB上的一点,D为BC的中点,DN=BC.
(1)求证CN⊥AB.
(2)若∠A=55°,则∠MDN= °.
解答:(1)证明:∵BM⊥AC,点D是BC的中点,∴BD=CD=DM=BC,
∵DN=BC,∴DM=DN=BD=CD,∴∠DBN=∠BND,∠DNC=∠DCN,
∵∠NBD+∠BNC+∠NCD=180°,∴2∠BND+2∠CND=180°,
∴∠BND+∠CND=90°,即∠CNB=90°,∴CN⊥AB;
(2)解:∵BM⊥AC,CN⊥AB,∴∠BNC=∠BMC=90°,
∵D为BC的中点,∴DN=BD,DM=CD,∴∠BND=∠NBD,∠DMC=∠MCD,
∴∠BND+∠DMC=∠ABC+∠ACB=180°﹣∠A=125°,
∴∠AND+∠AMD=360°﹣125°=235°,∴∠MDN=360°﹣∠A﹣∠AND﹣∠AMD=70°,
故答案为:70.
26、如图,在△ABC中,点D在BC上,AD平分∠BAC,点E、F分别在AC、AB上,满足AE=BF,
DE∥AB.求证:(1)AE=DE;(2)BD=EF.
解:(1)证明:∵AD平分∠BAC,∴∠BAD=∠EAD,
∵DE∥AB,∴∠BAD=∠ADE,∴∠EAD=∠ADE,∴AE=DE;
(2)证明:由(1)知,AE=DE.
又AE=BF,∴BF=DE.
又DE∥AB,∴∠BFD=∠EDF.
在△BFD与△EDF中,,∴△BFD≌△EDF(SAS),∴BD=EF.
27、如图,在△ABC中,点E是BC边上的一点,连接AE,BD垂直平分AE,垂足为F,交AC于点D,连接DE
(1)若△ABC的周长为18,△DEC的周长为6,求AB的长;
(2)若∠ABC=29°,∠C=47°,求∠CDE度数.
解:(1)∵BD垂直平分AE,∴AB=BE,AD=DE,
∵△ABC的周长为18,△DEC的周长为6,∴AB+BE+AD+CD+CE=18,CD+CE+DE=6,
∴2AB=18﹣6=12,∴AB=6;
(2)∵∠ABC=29°,∠C=47°,∴∠BAC=104°,
∵AB=BE,∠ABC=29°,∴∠BAE=∠AEB=,
∴∠DAE=∠BAC﹣∠BAE=104°﹣=,
∵AD=DE,∴∠DAE=∠DEA,∴∠CDE=2∠DAE=57°.
28、如图,已知BD为∠ABC的平分线,DE⊥BC于点E,且AB+BC=2BE.
(1)求证:∠BAD+∠BCD=180°;
(2)若将条件“AB+BC=2BE”与结论“∠BAD+∠BCD=180°”互换,结论成立吗?请说明理由.
【解析】 (1)过点D作DF⊥BA于点F.
∵AB+BC=2BE,∴AB=BE+BE-BC=BE+BE-BE-EC=BE-EC,即AB+EC=BE.
∵BD为∠ABC的平分线,DE⊥BC,DF⊥BA,∴DF=DE.
在Rt△BFD和Rt△BED中, ∴Rt△BFD≌Rt△BED(HL),∴BF=BE,∴AB+AF=BE.
∵AB+EC=BE,∴AF=EC.
在△AFD和△CED中, ∴△AFD≌△CED(SAS),∴∠DAF=∠DCE.
∵∠BAD+∠DAF=180°,∴∠BAD+∠BCD=180°.
(2)结论成立.理由如下:
过点D作DF⊥BA于点F.
∵∠BAD+∠DAF=180°,∠BAD+∠BCD=180°,∴∠DCE=∠DAF.
∵BD为∠ABC的平分线,DE⊥BC,DF⊥BA,∴∠DFA=∠DEC=90°,DF=DE.
在△AFD和△CED中 , ∴△AFD≌△CED(AAS),∴AF=CE.
在Rt△BFD和Rt△BED中, ∴Rt△BFD≌Rt△BED(HL),∴BF=BE,∴AB+AF=BE,
∴AB=BE-AF=BE-CE=BE-(BC-BE)=BE-BC+BE=2BE-BC, 即AB+BC=2BE.
一、选择题
1、等腰三角形中有一个角为100°,则其底角为( )
A.50° B.40° C.40°或100° D.50°或100°
2、已知等腰三角形有一边长为5,一边长为2,则其周长为( )
A.12 B.9 C.10 D.12或9
3、如图,在Rt△ABC中,∠C=90°,∠B=30°,CD是斜边AB上的高,AD=3cm,则AB的长度是( )
A.3cm B.6cm C.9cm D.12cm
4、如图,点D在△ABC的边BC上,且BC=BD+AD,则点D在( )的垂直平分线上.
A.AB B.AC C.BC D.不能确定
5、如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是( )
A.ED=CD B.∠DAC=∠B C.∠C>2∠B D.∠B+∠ADE=90°
6、如图,已知△ABC的周长是18cm,∠ABC和∠ACB的角平分线交于点O,OD⊥BC于点D,若OD=3cm,则△ABC的面积是( )cm2.
A.24 B.27 C.30 D.33
7、如图,BM是∠ABC的平分线,点D是BM上一点,点P为直线BC上的一个动点.若△ABD的面积为9,AB=6,则线段DP的长不可能是( )
A.2 B.3 C.4 D.5.5
8、如图所示,在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P,BE=BC,PG∥AD交BC于F,交AB于G,连接CP.下列结论:①∠ACB=2∠APB;②S△PAC:S△PAB=PC:PB;③BP垂直平分CE;④∠PCF=∠CPF.其中正确的有( )
A.①②④ B.①③④ C.②③④ D.①③
9、如图,AD平分∠BAC,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF.
则下列结论中:①AD是△ABC的高;②AD是△ABC的中线;③ED=FD;④AB=AE+BF.
其中正确的个数有( )
A.4个 B.3个 C.2个 D.1个
10、如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则B6B7的边长为( )
A.6 B.12 C.32 D.64
二、填空题
11、在△ABC中,AB=AC,∠A=40°,则∠B的度数为 °.
12、Rt△ABC中,∠C=90°,点D是斜边AB的中点,若CD=2,则AB= .
13、如图,在平面直角坐标系中,△ABO是边长为2的等边三角形,则A点的坐标是 .
14、如图,线段AB、BC的垂直平分线l1、l2相交于点O,若∠AOC=90°,∠A=13°,则∠C= °.
15、如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,DF⊥AC于点F,S△ABC=7,DE=2,AB=4,则AC长是 .
16、如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于E点,∠B=50°,∠FAE=20°,
则∠C= 度.
17、如图,在△ABC中,∠B=∠C,D,E分别是线段BC、AC上的一点,且AD=AE.
用等式表示∠1和∠2之间的数量关系是 .
18、如图所示,在△ABC中,∠C=90°,DE垂直平分AB,交BC于点E,垂足为点D,BE=8,∠B=15°,则EC的长为 .
19、如图,已知△ABC中高AD恰好平分边BC,∠B=30°,点P是BA延长线上一点,点
O是线段AD上一点且OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP.其中正确的为 .(填序号)
20、如图,四边形ABCD中,对角线AC、BD相交于点E,若∠ABD=∠ADC=90°,AC平分∠DAB,DE=4,BC=,则AE的长为 .
三、解答题
21、已知△ABC中,D为边BC上一点,AB=AD=CD.
(1)试说明∠ABC=2∠C;
(2)过点B作AD的平行线交CA的延长线于点E,若AD平分∠BAC,求证:AE=AB.
22、如图,在Rt△ABC中,∠C=90°,AC=6,AB=10,DE垂直平分AB,分别交AB、BC于点D、E.求CE的长.
23、已知:如图,在等腰三角形ADC中,AD=CD,且AB∥DC,CB⊥AB于B,CE⊥AD交AD的延长线于E.
(1)求证:CE=CB;
(2)如果连接BE,请写出BE与AC的关系并证明.
24、如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠BAD= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状也在改变,判断当∠BDA等于多少度时,△ADE是等腰三角形.
25、如图,在△ABC中,BM⊥AC,垂足为M.N为AB上的一点,D为BC的中点,DN=BC.
(1)求证CN⊥AB.
(2)若∠A=55°,则∠MDN= °.
26、如图,在△ABC中,点D在BC上,AD平分∠BAC,点E、F分别在AC、AB上,满足AE=BF,
DE∥AB.求证:(1)AE=DE;(2)BD=EF.
27、如图,在△ABC中,点E是BC边上的一点,连接AE,BD垂直平分AE,垂足为F,交AC于点D,连接DE
(1)若△ABC的周长为18,△DEC的周长为6,求AB的长;
(2)若∠ABC=29°,∠C=47°,求∠CDE度数.
28、如图,已知BD为∠ABC的平分线,DE⊥BC于点E,且AB+BC=2BE.
(1)求证:∠BAD+∠BCD=180°;
(2)若将条件“AB+BC=2BE”与结论“∠BAD+∠BCD=180°”互换,结论成立吗?请说明理由.
(答案)
一、选择题
1、等腰三角形中有一个角为100°,则其底角为( )
A.50° B.40° C.40°或100° D.50°或100°
解:∵等腰三角形的一个角100°,∴100°的角是顶角,
∴底角是×(180°﹣100°)=40°,故选:B.
2、已知等腰三角形有一边长为5,一边长为2,则其周长为( )
A.12 B.9 C.10 D.12或9
解:①若5为腰长,2为底边长,
∵5,5,2能组成三角形,∴此时周长为:5+5+2=12;
②若2为腰长,5为底边长,
∵2+2=4<5,∴不能组成三角形,故舍去;
∴周长为12. 故选:A.
3、如图,在Rt△ABC中,∠C=90°,∠B=30°,CD是斜边AB上的高,AD=3cm,则AB的长度是( )
A.3cm B.6cm C.9cm D.12cm
解:在Rt△ABC中,
∵CD是斜边AB上的高,∴∠ADC=90°,∴∠ACD=∠B=30°(同角的余角相等),
∵AD=3cm,在Rt△ACD中,AC=2AD=6cm,
在Rt△ABC中,AB=2AC=12cm.∴AB的长度是12cm.故选:D.
4、如图,点D在△ABC的边BC上,且BC=BD+AD,则点D在( )的垂直平分线上.
A.AB B.AC C.BC D.不能确定
解:∵BC=BD+AD=BD+CD∴AD=CD
∴点D在AC的垂直平分线上.故选:B.
5、如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是( )
A.ED=CD B.∠DAC=∠B C.∠C>2∠B D.∠B+∠ADE=90°
解:∵DE是线段AB的垂直平分线,∴AD=BD.
∴∠B=∠BAD,∠ADE=∠BDE.∴∠B+∠ADE=90°
其它选项无法证明其是正确的.
故选:D.
6、如图,已知△ABC的周长是18cm,∠ABC和∠ACB的角平分线交于点O,OD⊥BC于点D,若OD=3cm,则△ABC的面积是( )cm2.
A.24 B.27 C.30 D.33
解:过O点作OE⊥AB于E,OF⊥AC于F,连接OA,如图,
∵OB平分∠ABC,OD⊥BC,OE⊥AB,∴OE=OD=3,
同理可得OF=OD=3,
∴S△ABC=S△OAB+S△OBC+S△OAC=×OE×AB+×OD×BC+×OF×AC=(AB+BC+AC),
∵△ABC的周长是18,∴S△ABC=×18=27(cm2).
故选:B.
7、如图,BM是∠ABC的平分线,点D是BM上一点,点P为直线BC上的一个动点.若△ABD的面积为9,AB=6,则线段DP的长不可能是( )
A.2 B.3 C.4 D.5.5
解:过点D作DE⊥AB于E,DF⊥BC于F,
∵△ABD的面积为9,AB=6,∴DE=,
∵BM是∠ABC的平分线,∴DE=3,∴DP≥3,故选:A.
8、如图所示,在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P,BE=BC,PG∥AD交BC于F,交AB于G,连接CP.下列结论:①∠ACB=2∠APB;②S△PAC:S△PAB=PC:PB;③BP垂直平分CE;④∠PCF=∠CPF.其中正确的有( )
A.①②④ B.①③④ C.②③④ D.①③
解:∵PA平分∠CAB,PB平分∠CBE,∴∠PAB=∠CAB,∠PBE=∠CBE,
∵∠CBE=∠CAB+∠ACB,∠PBE=∠PAB+∠APB,∴∠ACB=2∠APB;故①正确;
过P作PM⊥AB于M,PN⊥AC于N,PS⊥BC于S,∴PM=PN=PS,∴PC平分∠BCD,
∵S△PAC:S△PAB=(AC?PN):(AB?PM)=AC:AB;故②不正确;
∵BE=BC,BP平分∠CBE∴BP垂直平分CE(三线合一),故③正确;
∵PG∥AD,∴∠FPC=∠DCP
∵PC平分∠DCB,∴∠DCP=∠PCF,∴∠PCF=∠CPF,故④正确.
本题正确的有:①③④
故选:B.
9、如图,AD平分∠BAC,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF.
则下列结论中:①AD是△ABC的高;②AD是△ABC的中线;③ED=FD;④AB=AE+BF.
其中正确的个数有( )
A.4个 B.3个 C.2个 D.1个
解:∵BC恰好平分∠ABF,∴∠ABC=∠FBD,
∵AC∥BF,∴∠C=∠FBD,∴∠C=∠ABC,∴△ABC为等腰三角形,
∵AD平分∠BAC,∴AD⊥BC,CD=BD,所以①②正确;
过D点作DH⊥AB于H,如图,
∵AD平分∠BAC,DE⊥AC,DH⊥AB,∴DE=DH,
∵AC∥BF,DE⊥AC,∴DF⊥BF,
∵BD平分∠ABF,DH⊥AB,∴DH=DF,∴DE=DF,所以③正确;
在△ADE和△ADH中,,∴△ADE≌△ADH(HL),∴AH=AE,
同理可得BH=BF,∴AB=AH+BH=AE+BF,所以④正确.
故选:A.
10、如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则B6B7的边长为( )
A.6 B.12 C.32 D.64
解:∵△A1B1A2是等边三角形,∴A1B1=A2B1,∠3=∠4=∠12=60°,∴∠2=120°,
∵∠MON=30°,∴∠1=180°﹣120°﹣30°=30°,
又∵∠3=60°,∴∠5=180°﹣60°﹣30°=90°,
∵∠MON=∠1=30°,∴OA1=A1B1=1,∴A2B1=1,
∵△A2B2A3、△A3B3A4是等边三角形,∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,∴A2B2=2B1A2=2,B3A3=2B2A3,
∴A3B3=4B1A2=4,A4B4=8B1A2=8,A5B5=16B1A2=16,
以此类推:A7B7=26B1A2=26=64,B6A7==32,△B7B6A7是直角三角形,∠B7B6A7=90°,
∴B6B7===32.
故选:C.
二、填空题
11、在△ABC中,AB=AC,∠A=40°,则∠B的度数为 °.
解:∵AB=AC,∴∠B=∠C,
∵∠A=40°,∴∠B=(180°﹣40°)÷2=70°.故答案为:70.
12、Rt△ABC中,∠C=90°,点D是斜边AB的中点,若CD=2,则AB= .
解:在Rt△ABC中,点D是斜边AB的中点,CD=2,
∴AB=2CD=2×2=4,
故答案为:4.
13、如图,在平面直角坐标系中,△ABO是边长为2的等边三角形,则A点的坐标是 .
解:过A作AE⊥x轴于E,
∵△ABO是等边三角形,边长为2,∴OA=2,OE=BE=1,
在Rt△AEO中,由勾股定理得:AE===,
即点A的坐标为(1,﹣).故答案为:(1,﹣).
14、如图,线段AB、BC的垂直平分线l1、l2相交于点O,若∠AOC=90°,∠A=13°,则∠C= °.
解:如图,连接OB,
∵OD垂直平分AB,∴OA=OB,∴∠ABO=∠A=13°,
∴∠AOB=180°﹣13°﹣13°=154°,
∵∠AOB+∠BOC+∠AOC=360°,∴∠BOC=360°﹣90°﹣154°=116°,
∵OE垂直平分BC,∴∠C=∠OBC=(180°﹣116°)=32°.
故答案为:32.
15、如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,DF⊥AC于点F,S△ABC=7,DE=2,AB=4,则AC长是 .
解:∵AD是△ABC中∠BAC的角平分线,DE⊥AB,DF⊥AC,∴DE=DF,
∴S△ABC=×4×2+AC?2=7,解得AC=3. 故答案为:3.
16、如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于E点,∠B=50°,∠FAE=20°,
则∠C= 度.
解:∵DE是线段AC的垂直平分线,∴EA=EC,∴∠EAC=∠C,
∵AF平分∠BAC,
∴∠BAF=∠CAF=∠FAE+∠CAE=20°+∠C,
由三角形内角和定理得,∠B+∠BAC+∠C=180°,即50°+20°+∠C+20°+∠C+∠C=180°,
解得,∠C=30°, 故答案为:30.
17、如图,在△ABC中,∠B=∠C,D,E分别是线段BC、AC上的一点,且AD=AE.
用等式表示∠1和∠2之间的数量关系是 .
解:根据三角形外角的性质得:∠AED=∠CDE+∠C,∠ADC=∠B+∠BAD,
∵AD=AE,∴∠AED=∠ADE,
∵AB=AC,∴∠B=∠C,
∴∠B+∠BAD=∠EDC+∠C+∠CDE,即∠BAD=2∠CDE,∠1=2∠2.
故答案为:∠1=2∠2.
18、如图所示,在△ABC中,∠C=90°,DE垂直平分AB,交BC于点E,垂足为点D,BE=8,∠B=15°,则EC的长为 .
解:在△ABC中,∠ACB=90°,∠B=15°,∴∠BAC=90°﹣15°=75°,
∵DE垂直平分AB,BE=8,∴BE=AE=8,∴∠EAB=∠B=15°,
∴∠EAC=75°﹣15°=60°,
∵∠C=90°,∴∠AEC=30°,∴AC=AE=×8=4,∴EC=AC=4,
故答案为:.
19、如图,已知△ABC中高AD恰好平分边BC,∠B=30°,点P是BA延长线上一点,点
O是线段AD上一点且OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP.其中正确的为 .(填序号)
解:①连接OB,如图1,
∵△ABC中高AD恰好平分边BC,即AD是BC垂直平分线,∴AB=AC,BD=CD,
∴OB=OC=OP,∴∠APO=∠ABO,∠DBO=∠DCO,
∵∠ABC=∠ABO+∠DBO=30°,∴∠APO+∠DCO=30°.故①正确;
②△OBP中,∠BOP=180°﹣∠OPB﹣∠OBP,
△BOC中,∠BOC=180°﹣∠OBC﹣∠OCB,
∴∠POC=360°﹣∠BOP﹣∠BOC=∠OPB+∠OBP+∠OBC+∠OCB,
∵∠OPB=∠OBP,∠OBC=∠OCB,∴∠POC=2∠ABD=60°,
∵PO=OC,∴△OPC是等边三角形,故②正确;
③如图2,在AC上截取AE=PA,
∵∠PAE=180°﹣∠BAC=60°,∴△APE是等边三角形,
∴∠PEA=∠APE=60°,PE=PA,∴∠APO+∠OPE=60°,
∵∠OPE+∠CPE=∠CPO=60°,∴∠APO=∠CPE,
∵OP=CP,在△OPA和△CPE中,,∴△OPA≌△CPE(SAS),
∴AO=CE,∴AC=AE+CE=AO+AP;故③正确;
④如图3,作CH⊥BP,
∵∠HCB=60°,∠PCO=60°,∴∠PCH=∠OCD,
在△CDO和△CHP中,,∴△CDO≌△CHP(AAS),
∴S△OCD=S△CHP∴CH=CD,
∵CD=BD,∴BD=CH,
在Rt△ABD和Rt△ACH中,,∴Rt△ABD≌Rt△ACH(HL),∴S△ABD=S△AHC,
∵四边形OAPC面积=S△OAC+S△AHC+S△CHP,S△ABC=S△AOC+S△ABD+S△OCD
∴四边形OAPC面积=S△ABC.故④正确.
故答案为:①②③④.
20、如图,四边形ABCD中,对角线AC、BD相交于点E,若∠ABD=∠ADC=90°,AC平分∠DAB,DE=4,BC=,则AE的长为 .
解:过点C作CH⊥AB交AB的延长线于H,CJ⊥BD于J.
∵CA平分∠DAN,CD⊥AD,CH⊥AH,∴∠DAC=∠BAC,CD=CH,
∵∠ADC=∠ABD=90°,∴∠DAC+∠ACD=90°,∠CAB+∠AEB=90°,∴∠ACD=∠AEB,
∵∠DEC=∠AEB,∴∠DEC=∠DCE,∴DE=DC=CH=4,
∵∠CJB=∠JBH=∠H=90°,∴四边形BHCE是矩形,
∴BE=CH=4,EC=BH===,
∴DE===,
∴JE=DE﹣DJ=4﹣=,EB=BJ﹣EJ=4﹣=,
∴EC===,
∵CJ∥AB,∴=,∴=,∴AE=,
故答案为:
三、解答题
21、已知△ABC中,D为边BC上一点,AB=AD=CD.
(1)试说明∠ABC=2∠C;
(2)过点B作AD的平行线交CA的延长线于点E,若AD平分∠BAC,求证:AE=AB.
证明:(1)∵AB=AD,∴∠ABC=∠ADB,
∵AD=CD,∴∠DAC=∠C,
∵∠ADB=∠DAC+∠C=2∠C,∴∠ABC=2∠C;
(2)∵AD平分∠BAC,∴∠DAB=∠CAD,
∵BE∥AD,∴∠DAB=∠ABE,∠E=∠CAD,
∴∠ABE=∠E,∴AE=AB.
22、如图,在Rt△ABC中,∠C=90°,AC=6,AB=10,DE垂直平分AB,分别交AB、BC于点D、E.求CE的长.
解:在Rt△ABC中,∠C=90°,∴;
∵DE垂直平分AB,分别交AB、BC于点D、E,∴AE=BE;
设CE=x,则AE=BE=8﹣x;
在Rt△ACE中,∠C=90°,∴CE2+AC2=AE2;即x2+62=(8﹣x)2,
解得,即.
23、已知:如图,在等腰三角形ADC中,AD=CD,且AB∥DC,CB⊥AB于B,CE⊥AD交AD的延长线于E.
(1)求证:CE=CB;
(2)如果连接BE,请写出BE与AC的关系并证明.
证明:(1)∵AD=CD,∴∠DAC=∠DCA,
∵AB∥CD,∴∠DCA=∠CAB,
∴∠DAC=∠CAB,∴AC是∠EAB的角平分线,
∵CE⊥AE,CB⊥AB,∴CE=CB;
( 2) AC垂直平分BE,
证明:由(1)知,CE=CB,
∵CE⊥AE,CB⊥AB,∴∠CEA=∠CBA=90°,
∵在Rt△CEA和Rt△CBA中,∴Rt△CEA≌Rt△CBA(HL),
∴AE=AB,CE=CB,
∴点A、点C在线段BE的垂直平分线上,∴AC垂直平分BE.
24、如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠BAD= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状也在改变,判断当∠BDA等于多少度时,△ADE是等腰三角形.
解:(1)∠BAD=180°﹣∠ABD﹣∠BDA=180°﹣40°﹣115°=25°;
从图中可以得知,点D从B向C运动时,∠BDA逐渐变小;
故答案为:25°;小.
(2∵∠EDC+∠EDA=∠DAB+∠B,∠B=∠EDA=40°,
∴∠EDC=∠DAB.,
∵∠B=∠C,∴当DC=AB=2时,△ABD≌△DCE,
(3)∵AB=AC,∴∠B=∠C=40°,
①当AD=AE时,∠ADE=∠AED=40°,
∵∠AED>∠C,∴此时不符合;
②当DA=DE时,即∠DAE=∠DEA=(180°﹣40°)=70°,
∵∠BAC=180°﹣40°﹣40°=100°,
∴∠BAD=100°﹣70°=30°;∴∠BDA=180°﹣30°﹣40°=110°;
③当EA=ED时,∠ADE=∠DAE=40°,
∴∠BAD=100°﹣40°=60°,∴∠BDA=180°﹣60°﹣40°=80°;
∴当∠ADB=110°或80°时,△ADE是等腰三角形.
25、如图,在△ABC中,BM⊥AC,垂足为M.N为AB上的一点,D为BC的中点,DN=BC.
(1)求证CN⊥AB.
(2)若∠A=55°,则∠MDN= °.
解答:(1)证明:∵BM⊥AC,点D是BC的中点,∴BD=CD=DM=BC,
∵DN=BC,∴DM=DN=BD=CD,∴∠DBN=∠BND,∠DNC=∠DCN,
∵∠NBD+∠BNC+∠NCD=180°,∴2∠BND+2∠CND=180°,
∴∠BND+∠CND=90°,即∠CNB=90°,∴CN⊥AB;
(2)解:∵BM⊥AC,CN⊥AB,∴∠BNC=∠BMC=90°,
∵D为BC的中点,∴DN=BD,DM=CD,∴∠BND=∠NBD,∠DMC=∠MCD,
∴∠BND+∠DMC=∠ABC+∠ACB=180°﹣∠A=125°,
∴∠AND+∠AMD=360°﹣125°=235°,∴∠MDN=360°﹣∠A﹣∠AND﹣∠AMD=70°,
故答案为:70.
26、如图,在△ABC中,点D在BC上,AD平分∠BAC,点E、F分别在AC、AB上,满足AE=BF,
DE∥AB.求证:(1)AE=DE;(2)BD=EF.
解:(1)证明:∵AD平分∠BAC,∴∠BAD=∠EAD,
∵DE∥AB,∴∠BAD=∠ADE,∴∠EAD=∠ADE,∴AE=DE;
(2)证明:由(1)知,AE=DE.
又AE=BF,∴BF=DE.
又DE∥AB,∴∠BFD=∠EDF.
在△BFD与△EDF中,,∴△BFD≌△EDF(SAS),∴BD=EF.
27、如图,在△ABC中,点E是BC边上的一点,连接AE,BD垂直平分AE,垂足为F,交AC于点D,连接DE
(1)若△ABC的周长为18,△DEC的周长为6,求AB的长;
(2)若∠ABC=29°,∠C=47°,求∠CDE度数.
解:(1)∵BD垂直平分AE,∴AB=BE,AD=DE,
∵△ABC的周长为18,△DEC的周长为6,∴AB+BE+AD+CD+CE=18,CD+CE+DE=6,
∴2AB=18﹣6=12,∴AB=6;
(2)∵∠ABC=29°,∠C=47°,∴∠BAC=104°,
∵AB=BE,∠ABC=29°,∴∠BAE=∠AEB=,
∴∠DAE=∠BAC﹣∠BAE=104°﹣=,
∵AD=DE,∴∠DAE=∠DEA,∴∠CDE=2∠DAE=57°.
28、如图,已知BD为∠ABC的平分线,DE⊥BC于点E,且AB+BC=2BE.
(1)求证:∠BAD+∠BCD=180°;
(2)若将条件“AB+BC=2BE”与结论“∠BAD+∠BCD=180°”互换,结论成立吗?请说明理由.
【解析】 (1)过点D作DF⊥BA于点F.
∵AB+BC=2BE,∴AB=BE+BE-BC=BE+BE-BE-EC=BE-EC,即AB+EC=BE.
∵BD为∠ABC的平分线,DE⊥BC,DF⊥BA,∴DF=DE.
在Rt△BFD和Rt△BED中, ∴Rt△BFD≌Rt△BED(HL),∴BF=BE,∴AB+AF=BE.
∵AB+EC=BE,∴AF=EC.
在△AFD和△CED中, ∴△AFD≌△CED(SAS),∴∠DAF=∠DCE.
∵∠BAD+∠DAF=180°,∴∠BAD+∠BCD=180°.
(2)结论成立.理由如下:
过点D作DF⊥BA于点F.
∵∠BAD+∠DAF=180°,∠BAD+∠BCD=180°,∴∠DCE=∠DAF.
∵BD为∠ABC的平分线,DE⊥BC,DF⊥BA,∴∠DFA=∠DEC=90°,DF=DE.
在△AFD和△CED中 , ∴△AFD≌△CED(AAS),∴AF=CE.
在Rt△BFD和Rt△BED中, ∴Rt△BFD≌Rt△BED(HL),∴BF=BE,∴AB+AF=BE,
∴AB=BE-AF=BE-CE=BE-(BC-BE)=BE-BC+BE=2BE-BC, 即AB+BC=2BE.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
