18.2.3 正方形 提升训练题(Word版 含答案)
文档属性
| 名称 | 18.2.3 正方形 提升训练题(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 487.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-28 00:00:00 | ||
图片预览




文档简介
18.2.3 正方形 提升训练题
一、选择题
1.矩形,菱形,正方形都具有的性质是( )
A.每一条对角线平分一组对角
B.对角线相等
C.对角线互相平分
D.对角线互相垂直
2.正方形ABCD中,对角线AC、BD交于点O,则∠CBO等于( )
A.30° B.45° C.60° D.75°
3.下列说法正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线相等的四边形是矩形
C.每一条对角线都平分一组对角的四边形是菱形
D.对角线互相垂直且相等的四边形是正方形
4.平行四边形ABCD各边中点依次是E、F、G、H,关于四边形EFGH,下面结论一定成立的是( )
A.有一个内角等于90° B.有一组邻边相等 C.对角线互相垂直 D.对角线互相平分
5.四边形ABCD的对角线AC与BD相等且互相垂直,则顺次连接这个四边形四边的中点得到四边形是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
6.正方形具有而菱形不具有的性质是( )
A.对角线垂直且互相平分 B.每一条对角线平分一组对角 C.对角线相等 D.对边相等
7.如图,已知四边形ABCD中,∠BAD=∠ABC=∠BCD=90°,下列条件能使四边形ABCD成为正方形的是( )
A.AC=BD B.AB⊥BC C.AD=BC D.AC⊥BD
8.如图,四边形false是正方形,O,D两点的坐标分别是false,false,点C在第一象限,则点C的坐标是( )
A.false B.false C.false D.false
9.如图,正方形ABCD的对角线相交于点false,则图中等腰直角三角形的个数为( )
A.4 B.6 C.8 D.10
10.如图,已知在正方形ABCD中,对角线AC与BD相交于点O,AE,DF分别是∠OAD与∠ODC的平分线,AE的延长线与DF相交于点G,则下列结论:①AG⊥DF;②EF∥AB;③AB=AF;④AB=2EF.其中正确的结论是( )
A.①② B.③④ C.①②③ D.①②③④
二、填空题
11.已知正方形的对角线长为 false,则这个正方形的面积是______.
12.正方形的边长为6,则该正方形的边心距是_____________.
13.正方形的一条对角线长为false,则这个正方形的面积为____________false.
14.已知正方形false的边长等于false,那么边false的中点false到对角线false的距离等于_______false.
15.如图,在正方形false的内侧,作等边false,则false的度数是________.
三、解答题
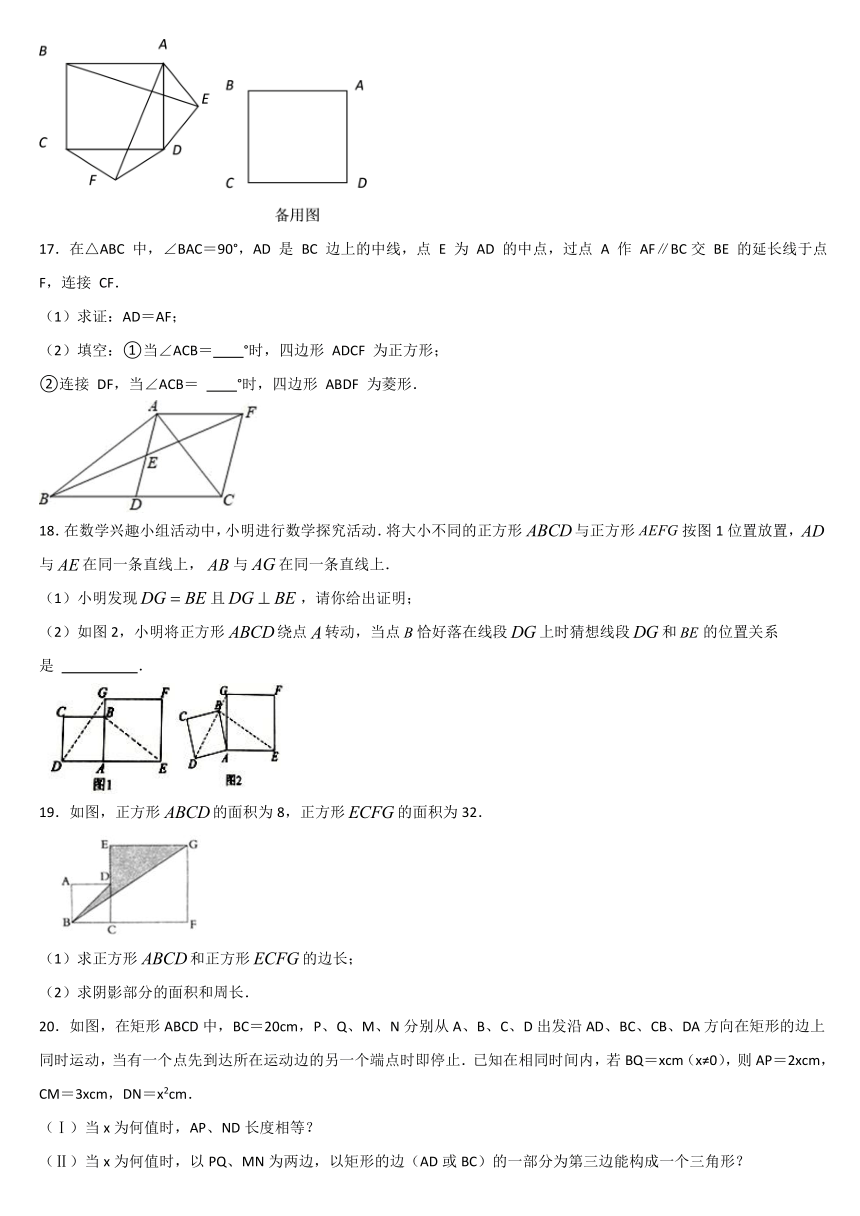
16.如图,在正方形ABCD的外侧, 作两个等腰三角形ADE和DCF,
(1) 若EA=ED=FD=FC,请判断BE和AF的关系?并给予证明.
(2)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,请用备用图画出图形,直接写出BE和AF的关系,不用证明.
17.在△ABC 中,∠BAC=90°,AD 是 BC 边上的中线,点 E 为 AD 的中点,过点 A 作 AF∥BC交 BE 的延长线于点 F,连接 CF.
(1)求证:AD=AF;
(2)填空:①当∠ACB= °时,四边形 ADCF 为正方形;
②连接 DF,当∠ACB= °时,四边形 ABDF 为菱形.
18.在数学兴趣小组活动中,小明进行数学探究活动.将大小不同的正方形false与正方形false按图1位置放置,false与false在同一条直线上,false与false在同一条直线上.
(1)小明发现false且false,请你给出证明;
(2)如图2,小明将正方形false绕点false转动,当点false恰好落在线段false上时猜想线段false和false的位置关系是 .
19.如图,正方形false的面积为8,正方形false的面积为32.
(1)求正方形false和正方形false的边长;
(2)求阴影部分的面积和周长.
20.如图,在矩形ABCD中,BC=20cm,P、Q、M、N分别从A、B、C、D出发沿AD、BC、CB、DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时即停止.已知在相同时间内,若BQ=xcm(x≠0),则AP=2xcm,CM=3xcm,DN=x2cm.
(Ⅰ)当x为何值时,AP、ND长度相等?
(Ⅱ)当x为何值时,以PQ、MN为两边,以矩形的边(AD或BC)的一部分为第三边能构成一个三角形?
(Ⅲ)当x为何值时,以P、Q、M、N为顶点的四边形是平行四边形?
21.定义:点P是四边形ABCD内一点,若三角形△PAB,△PBC,△PCD,△PDA均为等腰三角形,则称点P是四边形ABCD的一个“准中心”,如,正方形的中心就是它的一个“准中心”.
(1)如图,已知点P是正方形ABCD内的一点,且∠PBC=∠PCB=60°,证明点P是正四边形ABCD的一个“准中心”;
(2)填空:正方形ABCD共有 个“准中心”;
(3)已知∠BAD=60°,AB=AD=6,点C是∠BAD平分线上的动点,问在四边形ABCD的对角线AC上最多存在几个“准中心”点P(自行画出示意图),并求出每个“准中心”点P对应线段AC的长(精确到个位).
22.如图,false四个小球分别从正方形的四个顶点false处出发(小球的大小忽略不计),以同样的速度分别沿false方向滚动,其终点分别是点false,顺次连接四个小球所在的位置,得到四边形false.
(1)不论小球滚动多长时间,求证;四边形false总是正方形;
(2)这个四边形在什么时候面积最大?
(3)在什么时侯四边形false的面积为正方形false面积的一半?请说明理由.
23.如图,点false是正方形false边false.上一点,连接false,作false于点false,false于点false,连接false.
(1)求证:false;
(2)己知false,四边形false的面积为false,求false的值.
【参考答案】
1.C 2.B 3.C 4.D 5.D 6.C 7.D 8.D 9.C 10.C
11.25
12.3
13.false
14.false
15.false
16.(1)在正方形ABCD中,∠BAD=∠ADC=90false,AB=AD=CD.
∵EA=ED=FD=FC,
在△AED和△DFC中,
false,
∴△AED≌△DFC(SSS),
∴∠EAD=∠FDC.
∴∠BAD+∠EAD=∠ADC+∠FDC.
即∠BAE=∠ADF.
在△BAE和△ADF中,
false,
∴△BAE≌△ADF(SAS)
∴AF=BE,
∴∠ABE=∠DAF.
∵∠DAF+∠BAF=90false,
∴∠ABE+∠BAF=90false,
∴∠AMB=90false,
∴AF⊥BE.
故AF=BE,AF⊥BE.
(2)所画图形如图,AF=BE,AF⊥BE理由如下:
在△AED和△DFC中,
false,
∴△AED≌△DFC(SSS),
∴∠EAD=∠FDC.
∴∠BAD+∠EAD=∠ADC+∠FDC.即∠BAE=∠ADF.
在△BAE和△ADF中,false ,
∴△BAE≌△ADF(SAS),
∴AF=BE,
∴∠ABE=∠DAF.
∵∠DAF+∠BAF=90false,
∴∠ABE+∠BAF=90false,
∴∠AMB=90false,
∴AF⊥BE.
故AF=BE,AF⊥BE.
17.(1)∵∠BAC=90°,AD是BC边上的中线,
∵AD=CD=BD,
∵点E为AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,
∵∠AEF=∠DEB,
∴△AEF≌△DEB(AAS),
∴AF=BD,
∴AD=AF;
(2)①当∠ACB=45°时,四边形ADCF为正方形;
∵AD=AF,
∴AF=CD,
∵AF∥CD,
∴四边形ADCF是菱形,
要使四边形ADCF是正方形,
则∠DCF=90°,
∴∠ACD=∠ACF=45°;
②当∠ACB=30°时,四边形ABDF为菱形;
由(1)得AF=BD,AF∥BC,
∴四边形ABDF是平行四边形,
要使四边形ABDF为菱形,
∴AB=BD,
又∵AD =BD,
∴△ABD是等边三角形,
∴∠ABD=60°,
∴∠ACB=30°.
故答案为:45,30.
18.证明:(1)如图1,延长false交false于点false,
false 四边形false与四边形false是正方形,
false
在false与false中,
false,
false,
false,
false中,false
false
false中,false
false
false
(2)false
理由是:如图2,∵四边形ABCD和四边形AEFG都为正方形,
false
false,即false,
在false和false中,
false,
false
false
false
false
故答案为:false.
19.(1)∵false,false,
∴false,false,
答:正方形false和正方形false的边长分别是false和false;
(2)∵false,
∴false;
∴false;
又false,
∴false
falsefalse;
∵false,
false,false,
false,
∴false
false
false.
答:阴影部分的面积和周长分别是false和false.
20.(Ⅰ)∵false,
∴AP=ND时,即false,
解得:false或false(舍去),
∴当false为2时,AP、ND长度相等;
(Ⅱ)当点P与点N重合或点Q与点M重合时,以PQ,MN为两边,以矩形的边(AD或BC)的一部分为第三边可能构成一个三角形,
①当点P与点N重合时,
由题意得:false,
解得:false (舍去),
∵false,此时点Q与点M不重合,
∴false符合题意;
②当点Q与点M重合时,
由题意得:false,
解得:false,
此时false,不符合题意,
∴点Q与点M不能重合.
综上所述,所求false的值为:false;
(Ⅲ)∵当N点到达A点时,false,此时M点和Q点还未相遇,
∴点Q只能在点M的左侧,
①当点P在点N的左侧时,如图1所示:
由题意得:false,
解得:false (舍去),false,
当false时四边形PQMN是平行四边形;
②当点P在点N的右侧时,如图2所示:
由题意得:false,
解得:false(舍去),false,
当false时,四边形NQMP是平行四边形;
综上所述,当false或false时,以P,Q,M,N为顶点的四边形是平行四边形.
21.(1)∵ABCD为正方形,
∴∠ABC=∠BCD=∠CDA=∠DAB=90°,AB=BC=CD,
又∵∠PBC=∠PCB=60°,
∴∠BPC=60°,
∴PB=PC=BC=AB=CD,
∴PA=PD,
∴△PAB,△PBC,△PCD,△PDA均为等腰三角形,
∴点P是正方形ABCD的一个“准中心”.
(2)由(1)可知正方形ABCD有4个这样的“准中心”,再加上对角线的交点,即为5个“准中心”,
故答案为:5;
(3)在四边形ABCD的对角线AC上最多存在3个“准中心”点P;
①如图1,当PA=PB=PC=PD时,点P是“准中心”点,
∵∠BAD=60°,点C是∠BAD平分线上,
∴∠BAC=30°,
∴∠ACB=∠BPC=60°,∠ABC=90°,
则AC=false.
②如图2,当PA=BA=DA,PB=PC=PD时,点P是“准中心”点,
则PA=6,
∵∠BAD=60°,点C是∠BAD平分线上,
∴∠BAC=30°,
∴∠APB=75°,
∴∠PCB=false=37.5°,
作BE⊥AC于点E,
在Rt△AEB中,BE=falseAB=3,AE=ABfalse,
在Rt△CEB中,CE=false,
∴AC=AE+CE=false.
③如图3,当AB=PB=PC=PD=AD时,点P是“准中心”点,
此时四边形ABPD是菱形,连接BD,
则PA=2AE=2AB?cos30°=false,
∴AC=PA+PC=false.
综上,在四边形ABCD的对角线AC上最多存在3个“准中心”点P;AC长为4false或9或16.
22.解:(1)根据题意得false.
∵四边形false是正方形,
∴false°,
∴false.
∵在false和false中,
false,
∴false,
∴false,
∴四边形false为菱形,
∴false,
∴false,
∴四边形false为正方形.
(2)根据题意得当false在即将出发或到达终点时面积最大,此时false.
(3)当false分别在false的中点时,四边形false的面积为正方形false面积的一半.
理由如下:
设正方形false的边长为false,
则根据题意知false.
在false中,false.
由勾股定理,得false,
即false,解得false,
同理可得false.
∴当false四个小球分别在正方形false各边的中点时,四边形false的面积为正方形false面积的一半.
23.(1)证明:∵四边形ABCD为正方形,
∴BA=AD,∠BAD=90°,
∵DE⊥AM于点E,BF⊥AM于点F,
∴∠AFB=90°,∠DEA=90°,
∵∠ABF+∠BAF=90°,∠EAD+∠BAF=90°,
∴∠ABF=∠EAD,
在△ABF和△DEA中
false,
∴△ABF≌△DAE(AAS),
∴BF=AE;
(2)设AE=x,则BF=x,DE=AF=2,
∵四边形ABED的面积为24,
∴false?x?x+false?x?2=24,
解得x1=6,x2=﹣8(舍去),
∴EF=x﹣2=4,
在Rt△BEF中,BE=false=2false,
∴false=false
一、选择题
1.矩形,菱形,正方形都具有的性质是( )
A.每一条对角线平分一组对角
B.对角线相等
C.对角线互相平分
D.对角线互相垂直
2.正方形ABCD中,对角线AC、BD交于点O,则∠CBO等于( )
A.30° B.45° C.60° D.75°
3.下列说法正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线相等的四边形是矩形
C.每一条对角线都平分一组对角的四边形是菱形
D.对角线互相垂直且相等的四边形是正方形
4.平行四边形ABCD各边中点依次是E、F、G、H,关于四边形EFGH,下面结论一定成立的是( )
A.有一个内角等于90° B.有一组邻边相等 C.对角线互相垂直 D.对角线互相平分
5.四边形ABCD的对角线AC与BD相等且互相垂直,则顺次连接这个四边形四边的中点得到四边形是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
6.正方形具有而菱形不具有的性质是( )
A.对角线垂直且互相平分 B.每一条对角线平分一组对角 C.对角线相等 D.对边相等
7.如图,已知四边形ABCD中,∠BAD=∠ABC=∠BCD=90°,下列条件能使四边形ABCD成为正方形的是( )
A.AC=BD B.AB⊥BC C.AD=BC D.AC⊥BD
8.如图,四边形false是正方形,O,D两点的坐标分别是false,false,点C在第一象限,则点C的坐标是( )
A.false B.false C.false D.false
9.如图,正方形ABCD的对角线相交于点false,则图中等腰直角三角形的个数为( )
A.4 B.6 C.8 D.10
10.如图,已知在正方形ABCD中,对角线AC与BD相交于点O,AE,DF分别是∠OAD与∠ODC的平分线,AE的延长线与DF相交于点G,则下列结论:①AG⊥DF;②EF∥AB;③AB=AF;④AB=2EF.其中正确的结论是( )
A.①② B.③④ C.①②③ D.①②③④
二、填空题
11.已知正方形的对角线长为 false,则这个正方形的面积是______.
12.正方形的边长为6,则该正方形的边心距是_____________.
13.正方形的一条对角线长为false,则这个正方形的面积为____________false.
14.已知正方形false的边长等于false,那么边false的中点false到对角线false的距离等于_______false.
15.如图,在正方形false的内侧,作等边false,则false的度数是________.
三、解答题
16.如图,在正方形ABCD的外侧, 作两个等腰三角形ADE和DCF,
(1) 若EA=ED=FD=FC,请判断BE和AF的关系?并给予证明.
(2)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,请用备用图画出图形,直接写出BE和AF的关系,不用证明.
17.在△ABC 中,∠BAC=90°,AD 是 BC 边上的中线,点 E 为 AD 的中点,过点 A 作 AF∥BC交 BE 的延长线于点 F,连接 CF.
(1)求证:AD=AF;
(2)填空:①当∠ACB= °时,四边形 ADCF 为正方形;
②连接 DF,当∠ACB= °时,四边形 ABDF 为菱形.
18.在数学兴趣小组活动中,小明进行数学探究活动.将大小不同的正方形false与正方形false按图1位置放置,false与false在同一条直线上,false与false在同一条直线上.
(1)小明发现false且false,请你给出证明;
(2)如图2,小明将正方形false绕点false转动,当点false恰好落在线段false上时猜想线段false和false的位置关系是 .
19.如图,正方形false的面积为8,正方形false的面积为32.
(1)求正方形false和正方形false的边长;
(2)求阴影部分的面积和周长.
20.如图,在矩形ABCD中,BC=20cm,P、Q、M、N分别从A、B、C、D出发沿AD、BC、CB、DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时即停止.已知在相同时间内,若BQ=xcm(x≠0),则AP=2xcm,CM=3xcm,DN=x2cm.
(Ⅰ)当x为何值时,AP、ND长度相等?
(Ⅱ)当x为何值时,以PQ、MN为两边,以矩形的边(AD或BC)的一部分为第三边能构成一个三角形?
(Ⅲ)当x为何值时,以P、Q、M、N为顶点的四边形是平行四边形?
21.定义:点P是四边形ABCD内一点,若三角形△PAB,△PBC,△PCD,△PDA均为等腰三角形,则称点P是四边形ABCD的一个“准中心”,如,正方形的中心就是它的一个“准中心”.
(1)如图,已知点P是正方形ABCD内的一点,且∠PBC=∠PCB=60°,证明点P是正四边形ABCD的一个“准中心”;
(2)填空:正方形ABCD共有 个“准中心”;
(3)已知∠BAD=60°,AB=AD=6,点C是∠BAD平分线上的动点,问在四边形ABCD的对角线AC上最多存在几个“准中心”点P(自行画出示意图),并求出每个“准中心”点P对应线段AC的长(精确到个位).
22.如图,false四个小球分别从正方形的四个顶点false处出发(小球的大小忽略不计),以同样的速度分别沿false方向滚动,其终点分别是点false,顺次连接四个小球所在的位置,得到四边形false.
(1)不论小球滚动多长时间,求证;四边形false总是正方形;
(2)这个四边形在什么时候面积最大?
(3)在什么时侯四边形false的面积为正方形false面积的一半?请说明理由.
23.如图,点false是正方形false边false.上一点,连接false,作false于点false,false于点false,连接false.
(1)求证:false;
(2)己知false,四边形false的面积为false,求false的值.
【参考答案】
1.C 2.B 3.C 4.D 5.D 6.C 7.D 8.D 9.C 10.C
11.25
12.3
13.false
14.false
15.false
16.(1)在正方形ABCD中,∠BAD=∠ADC=90false,AB=AD=CD.
∵EA=ED=FD=FC,
在△AED和△DFC中,
false,
∴△AED≌△DFC(SSS),
∴∠EAD=∠FDC.
∴∠BAD+∠EAD=∠ADC+∠FDC.
即∠BAE=∠ADF.
在△BAE和△ADF中,
false,
∴△BAE≌△ADF(SAS)
∴AF=BE,
∴∠ABE=∠DAF.
∵∠DAF+∠BAF=90false,
∴∠ABE+∠BAF=90false,
∴∠AMB=90false,
∴AF⊥BE.
故AF=BE,AF⊥BE.
(2)所画图形如图,AF=BE,AF⊥BE理由如下:
在△AED和△DFC中,
false,
∴△AED≌△DFC(SSS),
∴∠EAD=∠FDC.
∴∠BAD+∠EAD=∠ADC+∠FDC.即∠BAE=∠ADF.
在△BAE和△ADF中,false ,
∴△BAE≌△ADF(SAS),
∴AF=BE,
∴∠ABE=∠DAF.
∵∠DAF+∠BAF=90false,
∴∠ABE+∠BAF=90false,
∴∠AMB=90false,
∴AF⊥BE.
故AF=BE,AF⊥BE.
17.(1)∵∠BAC=90°,AD是BC边上的中线,
∵AD=CD=BD,
∵点E为AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,
∵∠AEF=∠DEB,
∴△AEF≌△DEB(AAS),
∴AF=BD,
∴AD=AF;
(2)①当∠ACB=45°时,四边形ADCF为正方形;
∵AD=AF,
∴AF=CD,
∵AF∥CD,
∴四边形ADCF是菱形,
要使四边形ADCF是正方形,
则∠DCF=90°,
∴∠ACD=∠ACF=45°;
②当∠ACB=30°时,四边形ABDF为菱形;
由(1)得AF=BD,AF∥BC,
∴四边形ABDF是平行四边形,
要使四边形ABDF为菱形,
∴AB=BD,
又∵AD =BD,
∴△ABD是等边三角形,
∴∠ABD=60°,
∴∠ACB=30°.
故答案为:45,30.
18.证明:(1)如图1,延长false交false于点false,
false 四边形false与四边形false是正方形,
false
在false与false中,
false,
false,
false,
false中,false
false
false中,false
false
false
(2)false
理由是:如图2,∵四边形ABCD和四边形AEFG都为正方形,
false
false,即false,
在false和false中,
false,
false
false
false
false
故答案为:false.
19.(1)∵false,false,
∴false,false,
答:正方形false和正方形false的边长分别是false和false;
(2)∵false,
∴false;
∴false;
又false,
∴false
falsefalse;
∵false,
false,false,
false,
∴false
false
false.
答:阴影部分的面积和周长分别是false和false.
20.(Ⅰ)∵false,
∴AP=ND时,即false,
解得:false或false(舍去),
∴当false为2时,AP、ND长度相等;
(Ⅱ)当点P与点N重合或点Q与点M重合时,以PQ,MN为两边,以矩形的边(AD或BC)的一部分为第三边可能构成一个三角形,
①当点P与点N重合时,
由题意得:false,
解得:false (舍去),
∵false,此时点Q与点M不重合,
∴false符合题意;
②当点Q与点M重合时,
由题意得:false,
解得:false,
此时false,不符合题意,
∴点Q与点M不能重合.
综上所述,所求false的值为:false;
(Ⅲ)∵当N点到达A点时,false,此时M点和Q点还未相遇,
∴点Q只能在点M的左侧,
①当点P在点N的左侧时,如图1所示:
由题意得:false,
解得:false (舍去),false,
当false时四边形PQMN是平行四边形;
②当点P在点N的右侧时,如图2所示:
由题意得:false,
解得:false(舍去),false,
当false时,四边形NQMP是平行四边形;
综上所述,当false或false时,以P,Q,M,N为顶点的四边形是平行四边形.
21.(1)∵ABCD为正方形,
∴∠ABC=∠BCD=∠CDA=∠DAB=90°,AB=BC=CD,
又∵∠PBC=∠PCB=60°,
∴∠BPC=60°,
∴PB=PC=BC=AB=CD,
∴PA=PD,
∴△PAB,△PBC,△PCD,△PDA均为等腰三角形,
∴点P是正方形ABCD的一个“准中心”.
(2)由(1)可知正方形ABCD有4个这样的“准中心”,再加上对角线的交点,即为5个“准中心”,
故答案为:5;
(3)在四边形ABCD的对角线AC上最多存在3个“准中心”点P;
①如图1,当PA=PB=PC=PD时,点P是“准中心”点,
∵∠BAD=60°,点C是∠BAD平分线上,
∴∠BAC=30°,
∴∠ACB=∠BPC=60°,∠ABC=90°,
则AC=false.
②如图2,当PA=BA=DA,PB=PC=PD时,点P是“准中心”点,
则PA=6,
∵∠BAD=60°,点C是∠BAD平分线上,
∴∠BAC=30°,
∴∠APB=75°,
∴∠PCB=false=37.5°,
作BE⊥AC于点E,
在Rt△AEB中,BE=falseAB=3,AE=ABfalse,
在Rt△CEB中,CE=false,
∴AC=AE+CE=false.
③如图3,当AB=PB=PC=PD=AD时,点P是“准中心”点,
此时四边形ABPD是菱形,连接BD,
则PA=2AE=2AB?cos30°=false,
∴AC=PA+PC=false.
综上,在四边形ABCD的对角线AC上最多存在3个“准中心”点P;AC长为4false或9或16.
22.解:(1)根据题意得false.
∵四边形false是正方形,
∴false°,
∴false.
∵在false和false中,
false,
∴false,
∴false,
∴四边形false为菱形,
∴false,
∴false,
∴四边形false为正方形.
(2)根据题意得当false在即将出发或到达终点时面积最大,此时false.
(3)当false分别在false的中点时,四边形false的面积为正方形false面积的一半.
理由如下:
设正方形false的边长为false,
则根据题意知false.
在false中,false.
由勾股定理,得false,
即false,解得false,
同理可得false.
∴当false四个小球分别在正方形false各边的中点时,四边形false的面积为正方形false面积的一半.
23.(1)证明:∵四边形ABCD为正方形,
∴BA=AD,∠BAD=90°,
∵DE⊥AM于点E,BF⊥AM于点F,
∴∠AFB=90°,∠DEA=90°,
∵∠ABF+∠BAF=90°,∠EAD+∠BAF=90°,
∴∠ABF=∠EAD,
在△ABF和△DEA中
false,
∴△ABF≌△DAE(AAS),
∴BF=AE;
(2)设AE=x,则BF=x,DE=AF=2,
∵四边形ABED的面积为24,
∴false?x?x+false?x?2=24,
解得x1=6,x2=﹣8(舍去),
∴EF=x﹣2=4,
在Rt△BEF中,BE=false=2false,
∴false=false
