2020-2021学年苏科版数学九年级下册5.5用二 次函数解决问题 专项提升训练(一)(word版含答案)
文档属性
| 名称 | 2020-2021学年苏科版数学九年级下册5.5用二 次函数解决问题 专项提升训练(一)(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 127.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-28 00:00:00 | ||
图片预览




文档简介
【用二次函数解决问题】专项提升训练(一)
一.选择题
1.据省统计局公布的数据,安徽省2019年第二季度GDP总值约为7.9千亿元人民币,若我省第四季度GDP总值为y千亿元人民币,平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是( )
A.y=7.9(1+2x)
B.y=7.9(1﹣x)2
C.y=7.9(1+x)2
D.y=7.9+7.9(1+x)+7.9(1+x)2
2.如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m.水面上升1.5m,水面宽度为( )
A.1m
B.2m
C.m
D.m
3.某文学书的售价为每本30元,每星期可卖出200本,书店准备在年终进行降价促销.经市场调研发现,单价每下降2元,每星期可多卖出10本.设每本书降价x元后,每星期售出此文学书的销售额为y元,则y与x之间的函数关系式为( )
A.y=(30﹣x)(200+10x)
B.y=(30﹣x)(200+5x)
C.y=(30﹣x)(200﹣10x)
D.y=(30﹣x)(200﹣5x)
4.竖直上抛物体离地面的高度h(m)与运动时间t(s)之间的关系可以近似地用公式h=﹣5t2+v0t+h0表示,其中h0(m)是物体抛出时离地面的高度,v0(m/s)是物体抛出时的速度.某人将一个小球从距地面1.5m的高处以20m/s的速度竖直向上抛出,小球达到的离地面的最大高度为( )
A.23.5m
B.22.5m
C.21.5m
D.20.5m
5.今年由于受新型冠状病毒的影响,一次性医用口罩的销量剧增.某药店一月份销售量是5000枚,二、三两个月销售量连续增长.若月平均增长率为x,则该药店三月份销售口罩枚数y(枚)与x的函数关系式是( )
A.y=5000(1+x)
B.y=5000(1+x)2
C.y=5000(1+x2)
D.y=5000(1+2x)
6.“闻起来臭,吃起来香”的臭豆腐是长沙特色小吃,臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把“焦脆而不糊”的豆腐块数的百分比称为“可食用率”.在特定条件下,“可食用率”P与加工煎炸时间t(单位:分钟)近似满足的函数关系为:P=at2+bt+c(a≠0,a,b,c是常数),如图记录了三次实验的数据.根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为( )
A.3.50分钟
B.4.05分钟
C.3.75分钟
D.4.25分钟
7.如图所示,将一根长2m的铁丝首尾相接围成矩形,则矩形的面积与其一边满足的函数关系是( )
A.正比例函数关系
B.一次函数关系
C.二次函数关系
D.反比例函数关系
8.如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m,宽OC是4m.按照图中所示的平面直角坐标系,抛物线可以用y=﹣x2+bx+c表示.在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )
A.2m
B.4m
C.4
m
D.4m
9.Rt△ABC的三个顶点A,B,C均在抛物线y=x2上,并且斜边AB平行于x轴.若斜边上的高为h,则( )
A.h<1
B.h=1
C.1<h<2
D.h>2
10.烟花厂为成都春节特别设计制作了一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是.若这种礼炮在升空到最高点时引爆,则从点火升空到引爆需要的时间为( )
A.3s
B.4s
C.5s
D.6s
二.填空题
11.一位运动员投掷铅球,如果铅球运行时离地面的高度为y(米)关于水平距离x(米)的函数解析式为,那么该运动员的铅球投掷成绩为
米.
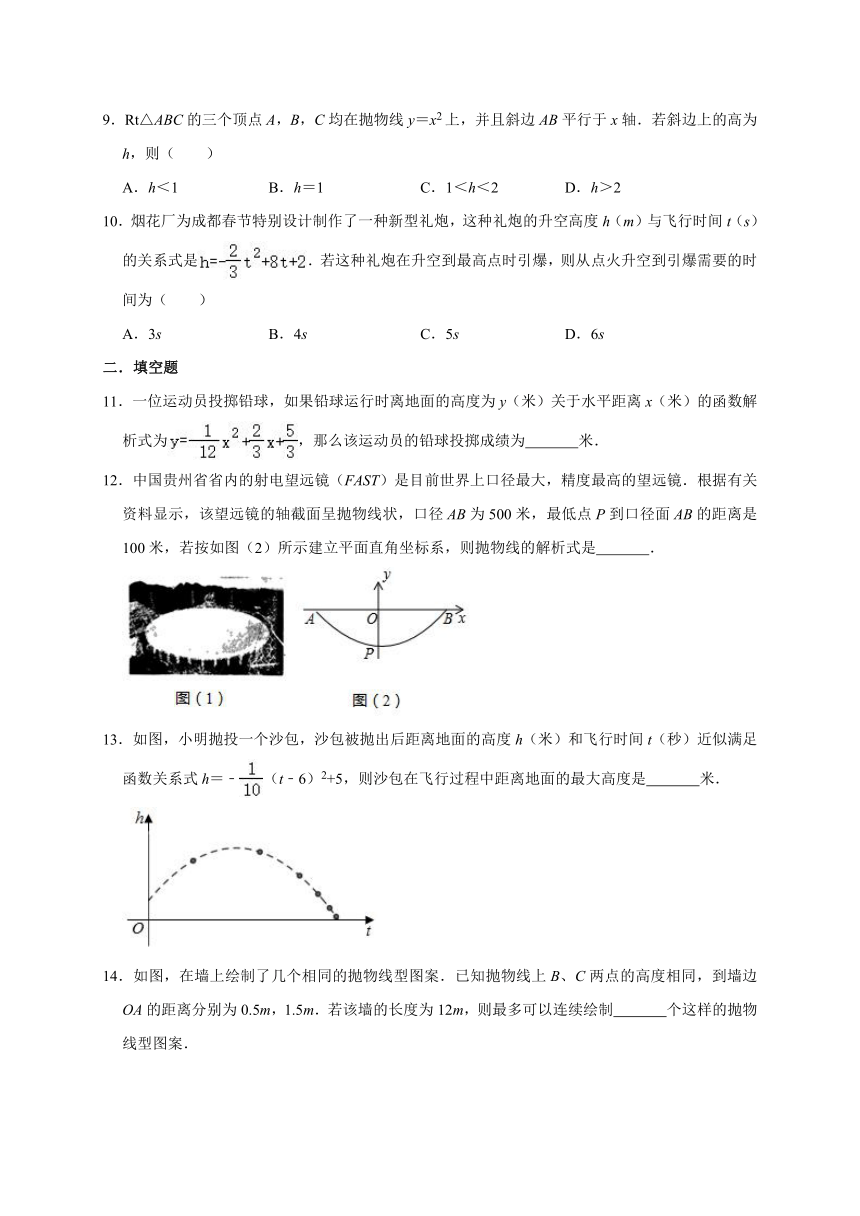
12.中国贵州省省内的射电望远镜(FAST)是目前世界上口径最大,精度最高的望远镜.根据有关资料显示,该望远镜的轴截面呈抛物线状,口径AB为500米,最低点P到口径面AB的距离是100米,若按如图(2)所示建立平面直角坐标系,则抛物线的解析式是
.
13.如图,小明抛投一个沙包,沙包被抛出后距离地面的高度h(米)和飞行时间t(秒)近似满足函数关系式h=﹣(t﹣6)2+5,则沙包在飞行过程中距离地面的最大高度是
米.
14.如图,在墙上绘制了几个相同的抛物线型图案.已知抛物线上B、C两点的高度相同,到墙边OA的距离分别为0.5m,1.5m.若该墙的长度为12m,则最多可以连续绘制
个这样的抛物线型图案.
15.在一定条件下,若物体运动的路程s(米)与时间t(秒)的关系式为s=5t2+2t,则当物体经过的路程是88米时,该物体所经过的时间为
秒.
三.解答题
16.某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线.已知跳板AB长为2米,跳板距水面CD高BC为3米,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度4米,现以CD为横轴,CB为纵轴建立直角坐标系.
(1)求这条抛物线的解析式;
(2)求运动员落水点与点C的距离.
17.某水果批发商经销一种水果,进货价是12元/千克,如果销售价定为22元/千克,每日可售出500千克;经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)若要每天销售盈利恰好为6000元,同时又可使顾客得到实惠,每千克应涨价为多少元?
(2)当销售价是多少时,每天的盈利最多?最多是多少?
18.如图,在一次高尔夫球的比赛中,某运动员在原点O处击球,目标是离击球点10米远的球洞,球的飞行路线是一条抛物线,结果球的落地点距离球洞2米(击球点、落地点、球洞三点共线),球在空中最高处达3.2米.
(1)求表示球飞行的高度y(单位:米)与表示球飞出的水平距离x(单位:米)之间的函数关系式;
(2)当球的飞行高度不低于3米时,求x的取值范围.
19.某商场以每个80元的价格进了一批玩具,当售价为120元时,商场平均每天可售出20个.为了扩大销售,增加盈利,商场决定采取降价措施,经调查发现:在一定范围内,玩具的单价每降低1元,商场每天可多售出2个.设每个玩具售价下降了x元,但售价不得低于玩具的进价,商场每天的销售利润为y元.
(1)降价后商场平均每天可售出
个玩具;
(2)求y与x的函数表达式,并直接写出自变量x的取值范围;
(3)商场将每个玩具的售价定为多少元时,可使每天获得的利润最大?最大利润是多少元?
20.已知直线l1:y=﹣2x+10交y轴于点A,交x轴于点B,二次函数的图象过A,B两点,交x轴于另一点C,BC=4,且对于该二次函数图象上的任意两点P1(x1,y1),P2(x2,y2),当x1>x2≥5时,总有y1>y2.
(1)求二次函数的表达式;
(2)若直线l2:y=mx+n(n≠10),求证:当m=﹣2时,l2∥l1;
(3)E为线段BC上不与端点重合的点,直线l3:y=﹣2x+q过点C且交直线AE于点F,求△ABE与△CEF面积之和的最小值.
参考答案
一.选择题
1.解:设平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是:y=7.9(1+x)2.
故选:C.
2.解:如右图建立平面直角坐标系,
设抛物线的解析式为y=ax2,
由已知可得,点(2,﹣2)在此抛物线上,
则﹣2=a×22,
解得a=﹣,
∴y=﹣x2,
当y=﹣0.5时,﹣x2=﹣0.5,
解得x=±1,
此时水面的宽度为2m,
故选:B.
3.解:设每本书降价x元,则每星期可售出(200+×10)=(200+5x)本,
∴每星期售出此文学书的销售额y=(30﹣x)(200+5x).
故选:B.
4.解:由题意可得,
h=﹣5t2+20t+1.5=﹣5(t﹣2)2+21.5,
因为a=﹣5<0,
故当t=2时,h取得最大值,此时h=21.5,
故选:C.
5.解:该药店三月份销售口罩枚数y(枚)与x的函数关系式是:y=5000(1+x)2.
故选:B.
6.解:将图象中的三个点(3,0.8)、(4,0.9)、(5,0.6)代入函数关系P=at2+bt+c中,
,
解得,
所以函数关系式为:P=﹣0.2t2+1.5t﹣1.9,
由题意可知:加工煎炸臭豆腐的最佳时间为抛物线顶点的横坐标:
t=﹣=﹣=3.75,
则当t=3.75分钟时,可以得到最佳时间.
故选:C.
7.解:设矩形的一边长为xm,则另一边的长为(2÷2﹣x)m,令矩形的面积为ym2,由题意得:
y=x(2÷2﹣x)
=x(1﹣x)
=﹣x2+x,
∴矩形的面积与其一边满足的函数关系是y=﹣x2+x,即满足二次函数关系.
故选:C.
8.解:根据题意,得
OA=12,OC=4.
所以抛物线的顶点横坐标为6,
即﹣==6,
∴b=2,
∵C(0,4),
∴c=4,
所以抛物线解析式为:
y=﹣x2+2x+4
=﹣(x﹣6)2+10
当y=8时,
8=﹣(x﹣6)2+10,
解得x1=6+2,x2=6﹣2.
则x1﹣x2=4.
所以两排灯的水平距离最小是4.
故选:D.
9.解:由题A,B,C均在抛物线y=x2上,并且斜边AB平行于x轴,
知A、B两点关于y轴对称,记斜边AB交y轴于点D,
可设A(﹣,b),B(,b),C(a,a2),D(0,b)
则因斜边上的高为h,
故:h=b﹣a2,
∵△ABC是直角三角形,由其性质直角三角形斜边中线等于斜边一半,
∴得CD=
∴=,方程两边平方得:(b﹣a2)=(a2﹣b)2
即h=(﹣h)2
因h>0,得h=1,是个定值.
故选:B.
10.解:∵礼炮在点火升空到最高点引爆,
∴t=﹣==6(s),
故选:D.
二.填空题
11.解:令=0,
解得x=10或﹣2(舍去﹣2),
故答案为10.
12.解:由题意可得:A(﹣250,0),P(0,﹣100),
设抛物线解析式为:y=ax2﹣100,
则0=62500a﹣100,
解得:a=,
故抛物线解析式为:y=x2﹣100.
故答案为:y=x2﹣100.
13.解:∵h=﹣(t﹣6)2+5为开口向下的抛物线,
∴当t=6时,h最大=5.
故答案为:5.
14.解:以点O为原点,建立如下坐标系,
由函数的图象知,点B、C的纵坐标相同,其横坐标分别为x=0.5和x=1.5,
故函数的对称轴为x=(0.5+1.5)=1,
设第一个图案与x轴交点为D,则OD=2,
则12÷2=6,
故最多可以连续绘制6个这样的抛物线型图案,
故答案为6.
15.解:把s=88代入s=5t2+2t得:
5t2+2t=88.
解得t1=4,t2=﹣4.4(舍去),
即t=4秒.
故答案为:4.
三.解答题
16.解:(1)如图所示,建立平面直角坐标系,
由题意可得抛物线的顶点坐标为(3,4),点A坐标为(2,3),
设抛物线的解析式为y=a(x﹣3)2+4,
将点A坐标(2,3)代入得:3=a(2﹣3)2+4,
解得:a=﹣1,
∴这条抛物线的解析式为y=﹣(x﹣3)2+4;
(2)∵y=﹣(x﹣3)2+4,
∴令y=0得:0=﹣(x﹣3)2+4,
解得:x1=1,x2=5,
∵起跳点A坐标为(2,3),
∴x1=1,不符合题意,
∴x=5,
∴运动员落水点与点C的距离为5米.
17.解:(1)设每千克应涨价为x元,由题意得:
(22﹣12+x)(500﹣20x)=6000,
整理得:x2﹣15x+50=0,
解得:x1=5,x2=10.
∵要使顾客得到实惠,
∴x=5.
∴每千克应涨价5元.
(2)设销售价为a元时,每天的盈利为w,由题意得:
w=(a﹣12)[500﹣20(a﹣22)]
=﹣20a2+1180a﹣11280
=﹣20+6125,
∵二次项系数为负,抛物线开口向下,
∴当a=时,w有最大值为6125.
∴当销售价是时,每天的盈利最多,最多是6125元.
18.解:(1)由题意可知,点(0,0),(8,0)在抛物线上,
∴设y与x之间的函数关系式为y=ax(x﹣8),
将(4,3.2)代入得:3.2=a×4×(4﹣8),
解得:a=﹣0.2,
∴y=﹣0.2x(x﹣8)
=﹣0.2x2+1.6,
∴y与x之间的函数关系式为y=﹣0.2x2+1.6;
(2)令y=3得:
3=﹣0.2x2+1.6,
∴x2﹣8x+15=0,
∴(x﹣3)(x﹣5)=0,
解得:x1=3,x2=5,
∴当球的飞行高度不低于3米时,3≤x≤5.
19.解:(1)降价后商场平均每天可售出玩具数量为:20+2x;
(2)由题意得y=(120﹣x﹣80)(20+2x)=﹣2x2+60x+800,其中,x的取值范围是0<x≤40;
(3)y=﹣2x2+60x+800=﹣2(x﹣15)2+1250(0<x≤40),
∴当x=15时,y有最大值1250.
此时玩具的售价为120﹣15=105(元).
∴该商场将每个玩具的售价定为105元时,可使每天获得的利润最大,最大利润是1250元.
故答案为:(1)20+2x.
20.解:(1)∵直线l1:y=﹣2x+10交y轴于点A,交x轴于点B,
∴点A(0,10),点B(5,0),
∵BC=4,
∴点C(9,0)或点C(1,0),
∵点P1(x1,y1),P2(x2,y2),当x1>x2≥5时,总有y1>y2.
∴当x≥5时,y随x的增大而增大,
当抛物线过点C(9,0)时,则当5<x<7时,y随x的增大而减少,不合题意舍去,
当抛物线过点C(1,0)时,则当x>3时,y随x的增大而增大,符合题意,
∴设抛物线解析式为:y=a(x﹣1)(x﹣5),过点A(0,10),
∴10=5a,
∴a=2,
∴抛物线解析式为:y=2(x﹣1)(x﹣5)=2x2﹣12x+10;
方法二:设抛物线解析式为y=ax2+bx+c,
由题意可得:,
解得:,
∴抛物线解析式为:y=2x2﹣12x+10;
(2)当m=﹣2时,直线l2:y=﹣2x+n(n≠10),
∴直线l2:y=﹣2x+n(n≠10)与直线l1:y=﹣2x+10不重合,
假设l1与l2不平行,则l1与l2必相交,设交点为P(xP,yP),
∴
解得:n=10,
∵n=10与已知n≠10矛盾,
∴l1与l2不相交,
∴l2∥l1;
(3)如图,
、
∵直线l3:y=﹣2x+q过点C,
∴0=﹣2×1+q,
∴q=2,
∴直线l3解析式为:y=﹣2x+2,
∴l3∥l1,
∴CF∥AB,
∴∠ECF=∠ABE,∠CFE=∠BAE,
∴△CEF∽△BEA,
∴=()2,
设BE=t(0<t<4),则CE=4﹣t,
∴S△ABE=×t×10=5t,
∴S△CEF=()2×S△ABE=()2×5t=,
∴S△ABE+S△CEF=5t+=10t+﹣40=10(﹣)2+40﹣40,
∴当t=2时,S△ABE+S△CEF的最小值为40﹣40.
一.选择题
1.据省统计局公布的数据,安徽省2019年第二季度GDP总值约为7.9千亿元人民币,若我省第四季度GDP总值为y千亿元人民币,平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是( )
A.y=7.9(1+2x)
B.y=7.9(1﹣x)2
C.y=7.9(1+x)2
D.y=7.9+7.9(1+x)+7.9(1+x)2
2.如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m.水面上升1.5m,水面宽度为( )
A.1m
B.2m
C.m
D.m
3.某文学书的售价为每本30元,每星期可卖出200本,书店准备在年终进行降价促销.经市场调研发现,单价每下降2元,每星期可多卖出10本.设每本书降价x元后,每星期售出此文学书的销售额为y元,则y与x之间的函数关系式为( )
A.y=(30﹣x)(200+10x)
B.y=(30﹣x)(200+5x)
C.y=(30﹣x)(200﹣10x)
D.y=(30﹣x)(200﹣5x)
4.竖直上抛物体离地面的高度h(m)与运动时间t(s)之间的关系可以近似地用公式h=﹣5t2+v0t+h0表示,其中h0(m)是物体抛出时离地面的高度,v0(m/s)是物体抛出时的速度.某人将一个小球从距地面1.5m的高处以20m/s的速度竖直向上抛出,小球达到的离地面的最大高度为( )
A.23.5m
B.22.5m
C.21.5m
D.20.5m
5.今年由于受新型冠状病毒的影响,一次性医用口罩的销量剧增.某药店一月份销售量是5000枚,二、三两个月销售量连续增长.若月平均增长率为x,则该药店三月份销售口罩枚数y(枚)与x的函数关系式是( )
A.y=5000(1+x)
B.y=5000(1+x)2
C.y=5000(1+x2)
D.y=5000(1+2x)
6.“闻起来臭,吃起来香”的臭豆腐是长沙特色小吃,臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把“焦脆而不糊”的豆腐块数的百分比称为“可食用率”.在特定条件下,“可食用率”P与加工煎炸时间t(单位:分钟)近似满足的函数关系为:P=at2+bt+c(a≠0,a,b,c是常数),如图记录了三次实验的数据.根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为( )
A.3.50分钟
B.4.05分钟
C.3.75分钟
D.4.25分钟
7.如图所示,将一根长2m的铁丝首尾相接围成矩形,则矩形的面积与其一边满足的函数关系是( )
A.正比例函数关系
B.一次函数关系
C.二次函数关系
D.反比例函数关系
8.如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m,宽OC是4m.按照图中所示的平面直角坐标系,抛物线可以用y=﹣x2+bx+c表示.在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )
A.2m
B.4m
C.4
m
D.4m
9.Rt△ABC的三个顶点A,B,C均在抛物线y=x2上,并且斜边AB平行于x轴.若斜边上的高为h,则( )
A.h<1
B.h=1
C.1<h<2
D.h>2
10.烟花厂为成都春节特别设计制作了一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是.若这种礼炮在升空到最高点时引爆,则从点火升空到引爆需要的时间为( )
A.3s
B.4s
C.5s
D.6s
二.填空题
11.一位运动员投掷铅球,如果铅球运行时离地面的高度为y(米)关于水平距离x(米)的函数解析式为,那么该运动员的铅球投掷成绩为
米.
12.中国贵州省省内的射电望远镜(FAST)是目前世界上口径最大,精度最高的望远镜.根据有关资料显示,该望远镜的轴截面呈抛物线状,口径AB为500米,最低点P到口径面AB的距离是100米,若按如图(2)所示建立平面直角坐标系,则抛物线的解析式是
.
13.如图,小明抛投一个沙包,沙包被抛出后距离地面的高度h(米)和飞行时间t(秒)近似满足函数关系式h=﹣(t﹣6)2+5,则沙包在飞行过程中距离地面的最大高度是
米.
14.如图,在墙上绘制了几个相同的抛物线型图案.已知抛物线上B、C两点的高度相同,到墙边OA的距离分别为0.5m,1.5m.若该墙的长度为12m,则最多可以连续绘制
个这样的抛物线型图案.
15.在一定条件下,若物体运动的路程s(米)与时间t(秒)的关系式为s=5t2+2t,则当物体经过的路程是88米时,该物体所经过的时间为
秒.
三.解答题
16.某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线.已知跳板AB长为2米,跳板距水面CD高BC为3米,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度4米,现以CD为横轴,CB为纵轴建立直角坐标系.
(1)求这条抛物线的解析式;
(2)求运动员落水点与点C的距离.
17.某水果批发商经销一种水果,进货价是12元/千克,如果销售价定为22元/千克,每日可售出500千克;经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)若要每天销售盈利恰好为6000元,同时又可使顾客得到实惠,每千克应涨价为多少元?
(2)当销售价是多少时,每天的盈利最多?最多是多少?
18.如图,在一次高尔夫球的比赛中,某运动员在原点O处击球,目标是离击球点10米远的球洞,球的飞行路线是一条抛物线,结果球的落地点距离球洞2米(击球点、落地点、球洞三点共线),球在空中最高处达3.2米.
(1)求表示球飞行的高度y(单位:米)与表示球飞出的水平距离x(单位:米)之间的函数关系式;
(2)当球的飞行高度不低于3米时,求x的取值范围.
19.某商场以每个80元的价格进了一批玩具,当售价为120元时,商场平均每天可售出20个.为了扩大销售,增加盈利,商场决定采取降价措施,经调查发现:在一定范围内,玩具的单价每降低1元,商场每天可多售出2个.设每个玩具售价下降了x元,但售价不得低于玩具的进价,商场每天的销售利润为y元.
(1)降价后商场平均每天可售出
个玩具;
(2)求y与x的函数表达式,并直接写出自变量x的取值范围;
(3)商场将每个玩具的售价定为多少元时,可使每天获得的利润最大?最大利润是多少元?
20.已知直线l1:y=﹣2x+10交y轴于点A,交x轴于点B,二次函数的图象过A,B两点,交x轴于另一点C,BC=4,且对于该二次函数图象上的任意两点P1(x1,y1),P2(x2,y2),当x1>x2≥5时,总有y1>y2.
(1)求二次函数的表达式;
(2)若直线l2:y=mx+n(n≠10),求证:当m=﹣2时,l2∥l1;
(3)E为线段BC上不与端点重合的点,直线l3:y=﹣2x+q过点C且交直线AE于点F,求△ABE与△CEF面积之和的最小值.
参考答案
一.选择题
1.解:设平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是:y=7.9(1+x)2.
故选:C.
2.解:如右图建立平面直角坐标系,
设抛物线的解析式为y=ax2,
由已知可得,点(2,﹣2)在此抛物线上,
则﹣2=a×22,
解得a=﹣,
∴y=﹣x2,
当y=﹣0.5时,﹣x2=﹣0.5,
解得x=±1,
此时水面的宽度为2m,
故选:B.
3.解:设每本书降价x元,则每星期可售出(200+×10)=(200+5x)本,
∴每星期售出此文学书的销售额y=(30﹣x)(200+5x).
故选:B.
4.解:由题意可得,
h=﹣5t2+20t+1.5=﹣5(t﹣2)2+21.5,
因为a=﹣5<0,
故当t=2时,h取得最大值,此时h=21.5,
故选:C.
5.解:该药店三月份销售口罩枚数y(枚)与x的函数关系式是:y=5000(1+x)2.
故选:B.
6.解:将图象中的三个点(3,0.8)、(4,0.9)、(5,0.6)代入函数关系P=at2+bt+c中,
,
解得,
所以函数关系式为:P=﹣0.2t2+1.5t﹣1.9,
由题意可知:加工煎炸臭豆腐的最佳时间为抛物线顶点的横坐标:
t=﹣=﹣=3.75,
则当t=3.75分钟时,可以得到最佳时间.
故选:C.
7.解:设矩形的一边长为xm,则另一边的长为(2÷2﹣x)m,令矩形的面积为ym2,由题意得:
y=x(2÷2﹣x)
=x(1﹣x)
=﹣x2+x,
∴矩形的面积与其一边满足的函数关系是y=﹣x2+x,即满足二次函数关系.
故选:C.
8.解:根据题意,得
OA=12,OC=4.
所以抛物线的顶点横坐标为6,
即﹣==6,
∴b=2,
∵C(0,4),
∴c=4,
所以抛物线解析式为:
y=﹣x2+2x+4
=﹣(x﹣6)2+10
当y=8时,
8=﹣(x﹣6)2+10,
解得x1=6+2,x2=6﹣2.
则x1﹣x2=4.
所以两排灯的水平距离最小是4.
故选:D.
9.解:由题A,B,C均在抛物线y=x2上,并且斜边AB平行于x轴,
知A、B两点关于y轴对称,记斜边AB交y轴于点D,
可设A(﹣,b),B(,b),C(a,a2),D(0,b)
则因斜边上的高为h,
故:h=b﹣a2,
∵△ABC是直角三角形,由其性质直角三角形斜边中线等于斜边一半,
∴得CD=
∴=,方程两边平方得:(b﹣a2)=(a2﹣b)2
即h=(﹣h)2
因h>0,得h=1,是个定值.
故选:B.
10.解:∵礼炮在点火升空到最高点引爆,
∴t=﹣==6(s),
故选:D.
二.填空题
11.解:令=0,
解得x=10或﹣2(舍去﹣2),
故答案为10.
12.解:由题意可得:A(﹣250,0),P(0,﹣100),
设抛物线解析式为:y=ax2﹣100,
则0=62500a﹣100,
解得:a=,
故抛物线解析式为:y=x2﹣100.
故答案为:y=x2﹣100.
13.解:∵h=﹣(t﹣6)2+5为开口向下的抛物线,
∴当t=6时,h最大=5.
故答案为:5.
14.解:以点O为原点,建立如下坐标系,
由函数的图象知,点B、C的纵坐标相同,其横坐标分别为x=0.5和x=1.5,
故函数的对称轴为x=(0.5+1.5)=1,
设第一个图案与x轴交点为D,则OD=2,
则12÷2=6,
故最多可以连续绘制6个这样的抛物线型图案,
故答案为6.
15.解:把s=88代入s=5t2+2t得:
5t2+2t=88.
解得t1=4,t2=﹣4.4(舍去),
即t=4秒.
故答案为:4.
三.解答题
16.解:(1)如图所示,建立平面直角坐标系,
由题意可得抛物线的顶点坐标为(3,4),点A坐标为(2,3),
设抛物线的解析式为y=a(x﹣3)2+4,
将点A坐标(2,3)代入得:3=a(2﹣3)2+4,
解得:a=﹣1,
∴这条抛物线的解析式为y=﹣(x﹣3)2+4;
(2)∵y=﹣(x﹣3)2+4,
∴令y=0得:0=﹣(x﹣3)2+4,
解得:x1=1,x2=5,
∵起跳点A坐标为(2,3),
∴x1=1,不符合题意,
∴x=5,
∴运动员落水点与点C的距离为5米.
17.解:(1)设每千克应涨价为x元,由题意得:
(22﹣12+x)(500﹣20x)=6000,
整理得:x2﹣15x+50=0,
解得:x1=5,x2=10.
∵要使顾客得到实惠,
∴x=5.
∴每千克应涨价5元.
(2)设销售价为a元时,每天的盈利为w,由题意得:
w=(a﹣12)[500﹣20(a﹣22)]
=﹣20a2+1180a﹣11280
=﹣20+6125,
∵二次项系数为负,抛物线开口向下,
∴当a=时,w有最大值为6125.
∴当销售价是时,每天的盈利最多,最多是6125元.
18.解:(1)由题意可知,点(0,0),(8,0)在抛物线上,
∴设y与x之间的函数关系式为y=ax(x﹣8),
将(4,3.2)代入得:3.2=a×4×(4﹣8),
解得:a=﹣0.2,
∴y=﹣0.2x(x﹣8)
=﹣0.2x2+1.6,
∴y与x之间的函数关系式为y=﹣0.2x2+1.6;
(2)令y=3得:
3=﹣0.2x2+1.6,
∴x2﹣8x+15=0,
∴(x﹣3)(x﹣5)=0,
解得:x1=3,x2=5,
∴当球的飞行高度不低于3米时,3≤x≤5.
19.解:(1)降价后商场平均每天可售出玩具数量为:20+2x;
(2)由题意得y=(120﹣x﹣80)(20+2x)=﹣2x2+60x+800,其中,x的取值范围是0<x≤40;
(3)y=﹣2x2+60x+800=﹣2(x﹣15)2+1250(0<x≤40),
∴当x=15时,y有最大值1250.
此时玩具的售价为120﹣15=105(元).
∴该商场将每个玩具的售价定为105元时,可使每天获得的利润最大,最大利润是1250元.
故答案为:(1)20+2x.
20.解:(1)∵直线l1:y=﹣2x+10交y轴于点A,交x轴于点B,
∴点A(0,10),点B(5,0),
∵BC=4,
∴点C(9,0)或点C(1,0),
∵点P1(x1,y1),P2(x2,y2),当x1>x2≥5时,总有y1>y2.
∴当x≥5时,y随x的增大而增大,
当抛物线过点C(9,0)时,则当5<x<7时,y随x的增大而减少,不合题意舍去,
当抛物线过点C(1,0)时,则当x>3时,y随x的增大而增大,符合题意,
∴设抛物线解析式为:y=a(x﹣1)(x﹣5),过点A(0,10),
∴10=5a,
∴a=2,
∴抛物线解析式为:y=2(x﹣1)(x﹣5)=2x2﹣12x+10;
方法二:设抛物线解析式为y=ax2+bx+c,
由题意可得:,
解得:,
∴抛物线解析式为:y=2x2﹣12x+10;
(2)当m=﹣2时,直线l2:y=﹣2x+n(n≠10),
∴直线l2:y=﹣2x+n(n≠10)与直线l1:y=﹣2x+10不重合,
假设l1与l2不平行,则l1与l2必相交,设交点为P(xP,yP),
∴
解得:n=10,
∵n=10与已知n≠10矛盾,
∴l1与l2不相交,
∴l2∥l1;
(3)如图,
、
∵直线l3:y=﹣2x+q过点C,
∴0=﹣2×1+q,
∴q=2,
∴直线l3解析式为:y=﹣2x+2,
∴l3∥l1,
∴CF∥AB,
∴∠ECF=∠ABE,∠CFE=∠BAE,
∴△CEF∽△BEA,
∴=()2,
设BE=t(0<t<4),则CE=4﹣t,
∴S△ABE=×t×10=5t,
∴S△CEF=()2×S△ABE=()2×5t=,
∴S△ABE+S△CEF=5t+=10t+﹣40=10(﹣)2+40﹣40,
∴当t=2时,S△ABE+S△CEF的最小值为40﹣40.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
