2020-2021学年高二下学期数学人教A版选修4-5第一讲含绝对值不等式的解法 课件(共21张PPT)
文档属性
| 名称 | 2020-2021学年高二下学期数学人教A版选修4-5第一讲含绝对值不等式的解法 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 941.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 09:48:48 | ||
图片预览








文档简介
(共21张PPT)
课前讲练
含绝对值不等式的解法
绝对值不等式的解法
教学目标:
知识目标:
1.理解含有一个绝对值的不等式的意义。
2.掌握含有一个绝对值的不等式的解法。
能力目标:
1.精确理解绝对值的定义,培养数形结合的能力。
2.在解题中,渗透转化与化归的思想,同时培养学生的抽象思维能力。
复习绝对值的意义:
|x|=
X>0
x
X=0
0
X<0
-
x
一个数的绝对值表示:
与这个数对应的点到
原点的距离,|x|≥0
A
x1
X
O
B
x2
|x1|
|x2|
=|OA|
=|OB|
代数的意义
几何意义
类比:|x|<3的解
|x|>3
的解
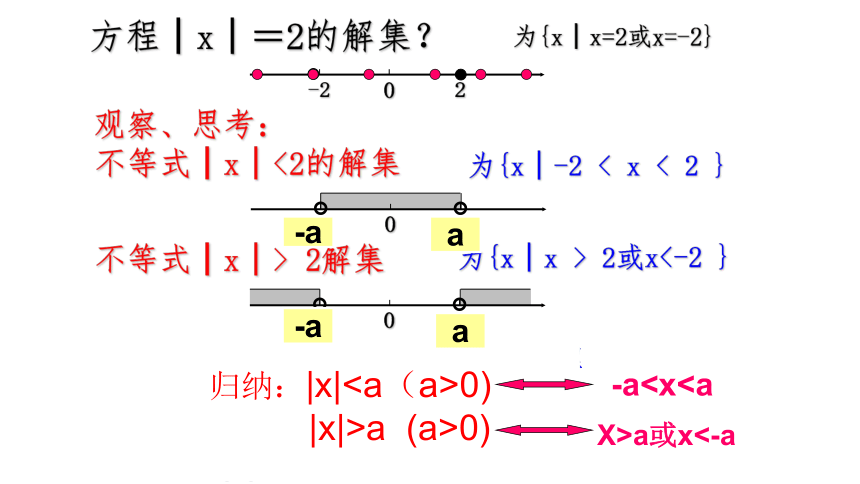
观察、思考:
不等式│x│<2的解集
方程│x│=2的解集?
为{x│x=2或x=-2}
0
2
-2
为{x│-2
<
x
<
2
}
不等式│x│>
2解集
为{x│x
>
2或x<-2
}
0
2
-2
0
2
-2
|x|<0的解
|x|>0的解
|x|<-2的解
|x|>-2的解
|x|<
的
解
|x|>
的解
归纳:|x|0)
|x|>a
(a>0)
-aX>a或x<-a
-a
a
-a
a
如果把|x|<2中的x换成“x-1”,也就是
|
x-1
|
<2如何解?
变式例题:
如果把|x|>2中的x换成“3x-1”,也就是
|
3x-1
|
>2如何解?
题型一:研究|ax+b|<(>)c型不等式
在这里,我们只要把ax+b看作是整体就可以了,此时可以得到:
练习:解不等式.
(1)|x-5|<8;
(2)|2x
+
3|>1.
解:(1)由原不等式可得-8∴-3∴原不等式的解集为{x|-3(2)由原不等式可得2x
+
3<
-1或2x
+
3
>1,
∴x<-2或x>-1
∴原不等式的解集为{x
|
x<-2或x>-1}.
解题总结:
2、归纳型如
|
f(x)||f(x)|>a(a>0)
不等式的解法。
1、采用了整体换元。
|
f(x)|-a|
f(x)|>a
f(x)<-a或f(x)>a
解不等式
|
5x-6
|
<
6
–
x
变式例题:型如
|
f(x)||f(x)|>a的不等式中
“a”用代数式替换,如何解?
|x|=
x
X<0
-
x
X≥0
思考二:是否可以转化为熟悉问题求解?
思考一:关键是去绝对值符号,能用定义吗?
5x-6
≥
0
5x-6<6-x
(Ⅰ)
或
(Ⅱ)
5x-6<0
-(5x-6)<6-x
解(Ⅰ)得:6/5≤x<2
解(Ⅱ)
得:0取它们的并集得:(0,2)
解不等式
|
5x-6
|
<
6
–
x
解:
解不等式
|
5x-6
|
<
6
–
x
解:
由绝对值的意义,原不等式转化为:
-(6-x)<5x-6<(6-x)
综合得0解(Ⅰ)得:0练习
(1)
;
(2)
|3x-1|>x+3.
例2、解不等式
1<︱3x+4︱≤6
解法一:原不等式可化为:
∴原不等式的解集为:
例2、解不等式
1<︱3x+4︱≤6
解法二:依绝对值的意义,原不等式等价于:
-6≤3x+4<-1
或
1<3x+4
≤6
∴原不等式的解集为:
比较此题的两种解法,解法二比较简单,解法二
去掉绝对值符号的依据是:
练习:
解不等式
3<|3-2x|≤5
.
0
3
-1
4
解不等式
3<|3-2x|≤5
.
0
3
-1
4
?
?
-
<
5
|
2
3
|
3
x
解法2:
题型:不等式n<|
ax
+
b
|
<m
(m>n>0)
的解集
方法一:等价于不等式组
方法二:几何意义
-m
-n
n
m
0
1.不等式1<|x+1|<3的解集是 ( )
A.(0,2) B.(-2,0)∪(2,4)
C.(-4,0)
D.(-4,-2)∪(0,2)
D
【解析】原不等式等价于1<x+1<3或-3<x+1<-1,
解得0<x<2或-4<x<-2.
练习
归纳:
课前讲练
含绝对值不等式的解法
绝对值不等式的解法
教学目标:
知识目标:
1.理解含有一个绝对值的不等式的意义。
2.掌握含有一个绝对值的不等式的解法。
能力目标:
1.精确理解绝对值的定义,培养数形结合的能力。
2.在解题中,渗透转化与化归的思想,同时培养学生的抽象思维能力。
复习绝对值的意义:
|x|=
X>0
x
X=0
0
X<0
-
x
一个数的绝对值表示:
与这个数对应的点到
原点的距离,|x|≥0
A
x1
X
O
B
x2
|x1|
|x2|
=|OA|
=|OB|
代数的意义
几何意义
类比:|x|<3的解
|x|>3
的解
观察、思考:
不等式│x│<2的解集
方程│x│=2的解集?
为{x│x=2或x=-2}
0
2
-2
为{x│-2
<
x
<
2
}
不等式│x│>
2解集
为{x│x
>
2或x<-2
}
0
2
-2
0
2
-2
|x|<0的解
|x|>0的解
|x|<-2的解
|x|>-2的解
|x|<
的
解
|x|>
的解
归纳:|x|
|x|>a
(a>0)
-a
-a
a
-a
a
如果把|x|<2中的x换成“x-1”,也就是
|
x-1
|
<2如何解?
变式例题:
如果把|x|>2中的x换成“3x-1”,也就是
|
3x-1
|
>2如何解?
题型一:研究|ax+b|<(>)c型不等式
在这里,我们只要把ax+b看作是整体就可以了,此时可以得到:
练习:解不等式.
(1)|x-5|<8;
(2)|2x
+
3|>1.
解:(1)由原不等式可得-8
+
3<
-1或2x
+
3
>1,
∴x<-2或x>-1
∴原不等式的解集为{x
|
x<-2或x>-1}.
解题总结:
2、归纳型如
|
f(x)|
不等式的解法。
1、采用了整体换元。
|
f(x)|
f(x)|>a
f(x)<-a或f(x)>a
解不等式
|
5x-6
|
<
6
–
x
变式例题:型如
|
f(x)|
“a”用代数式替换,如何解?
|x|=
x
X<0
-
x
X≥0
思考二:是否可以转化为熟悉问题求解?
思考一:关键是去绝对值符号,能用定义吗?
5x-6
≥
0
5x-6<6-x
(Ⅰ)
或
(Ⅱ)
5x-6<0
-(5x-6)<6-x
解(Ⅰ)得:6/5≤x<2
解(Ⅱ)
得:0
解不等式
|
5x-6
|
<
6
–
x
解:
解不等式
|
5x-6
|
<
6
–
x
解:
由绝对值的意义,原不等式转化为:
-(6-x)<5x-6<(6-x)
综合得0
(1)
;
(2)
|3x-1|>x+3.
例2、解不等式
1<︱3x+4︱≤6
解法一:原不等式可化为:
∴原不等式的解集为:
例2、解不等式
1<︱3x+4︱≤6
解法二:依绝对值的意义,原不等式等价于:
-6≤3x+4<-1
或
1<3x+4
≤6
∴原不等式的解集为:
比较此题的两种解法,解法二比较简单,解法二
去掉绝对值符号的依据是:
练习:
解不等式
3<|3-2x|≤5
.
0
3
-1
4
解不等式
3<|3-2x|≤5
.
0
3
-1
4
?
?
-
<
5
|
2
3
|
3
x
解法2:
题型:不等式n<|
ax
+
b
|
<m
(m>n>0)
的解集
方法一:等价于不等式组
方法二:几何意义
-m
-n
n
m
0
1.不等式1<|x+1|<3的解集是 ( )
A.(0,2) B.(-2,0)∪(2,4)
C.(-4,0)
D.(-4,-2)∪(0,2)
D
【解析】原不等式等价于1<x+1<3或-3<x+1<-1,
解得0<x<2或-4<x<-2.
练习
归纳:
