北师大版初中数学七年级下第二章相交线与平行线同步试卷(word版含解析)
文档属性
| 名称 | 北师大版初中数学七年级下第二章相交线与平行线同步试卷(word版含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 429.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-29 00:00:00 | ||
图片预览

文档简介
北师大版初中数学七年级下第二章同步试卷
考试时间:120分钟 满分:120分
姓名:__________ 班级:__________考号:__________
一、单选题(共10题;共30分)
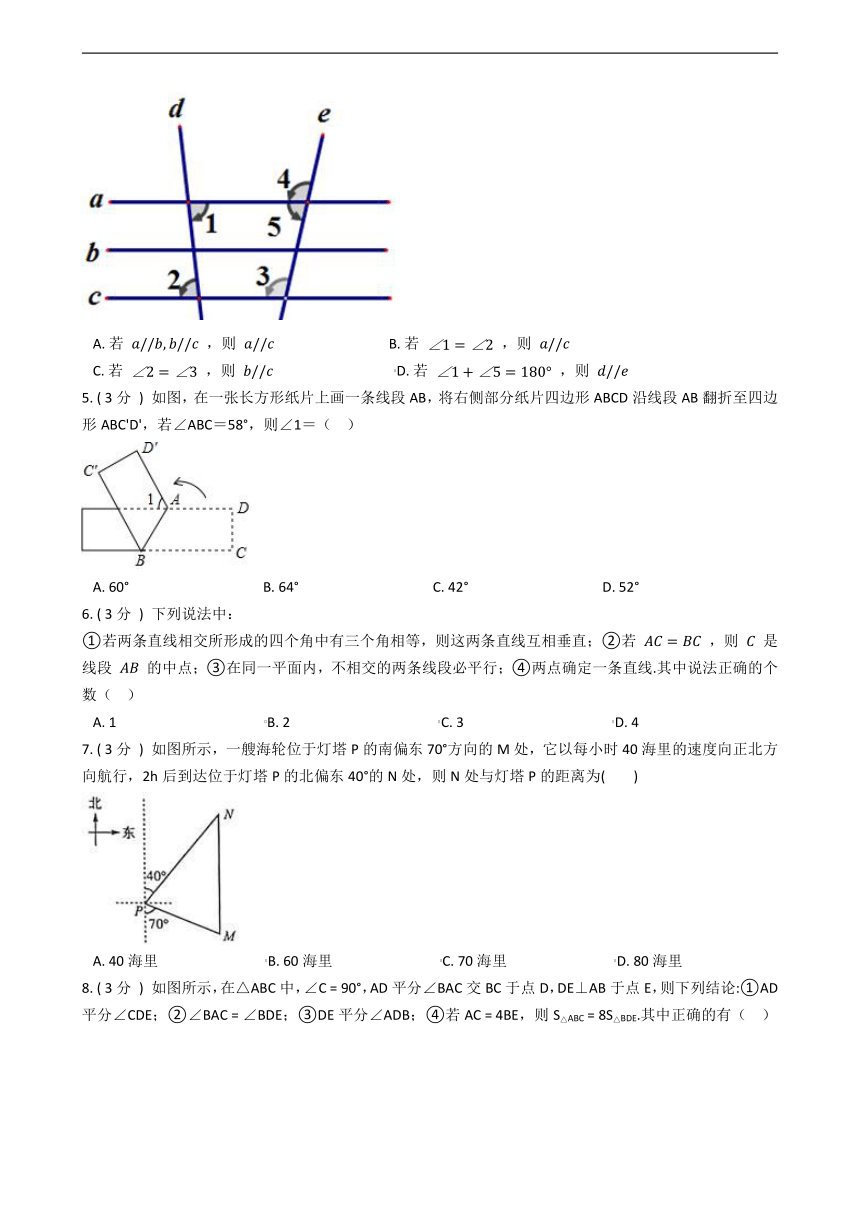
1. ( 3分 ) 如图,在 RtΔABC 中, ∠ACB=90° ,以其三边为边向外作正方形,过点 C 作 CR⊥FG 于点 R ,再过点 C 作 PQ⊥CR 分别交边 DE , BH 于点 P , Q .若 QH=2PE , PQ=15 ,则 CR 的长为 ( ?? )
A.?14???????????????????????????????????????B.?15???????????????????????????????????????C.?83???????????????????????????????????????D.?65
2. ( 3分 ) 如图,在△ABC中,∠A=90°,P是BC上一点,且DB=DC,过BC上一点P,作PE⊥AB于E,PF⊥DC于F,已知:AD:DB=1:3,BC= 46 ,则PE+PF的长是(?? )
A.?46??????????????????????????????????????B.?42??????????????????????????????????????C.?6??????????????????????????????????????D.?26
3. ( 3分 ) 如图,四边形ABCD内接于?O,连结对角线AC与BD交于点E,且BD为?O的直径,已知∠BDC=40°,∠AEB=110°,则∠ABC=(???? )
A.?65°???????????????????????????????????????B.?70°???????????????????????????????????????C.?75°???????????????????????????????????????D.?80°
4. ( 3分 ) 如图,下列说法错误的是(? )
A.?若 a//b,b//c ,则 a//c?????????????????????????????????B.?若 ∠1=∠2 ,则 a//c
C.?若 ∠2=∠3 ,则 b//c???????????????????????????????????D.?若 ∠1+∠5=180° ,则 d//e
5. ( 3分 ) 如图,在一张长方形纸片上画一条线段AB,将右侧部分纸片四边形ABCD沿线段AB翻折至四边形ABC'D',若∠ABC=58°,则∠1=(?? )
A.?60°???????????????????????????????????????B.?64°???????????????????????????????????????C.?42°???????????????????????????????????????D.?52°
6. ( 3分 ) 下列说法中:
①若两条直线相交所形成的四个角中有三个角相等,则这两条直线互相垂直;②若 AC=BC ,则 C 是线段 AB 的中点;③在同一平面内,不相交的两条线段必平行;④两点确定一条直线.其中说法正确的个数(?? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
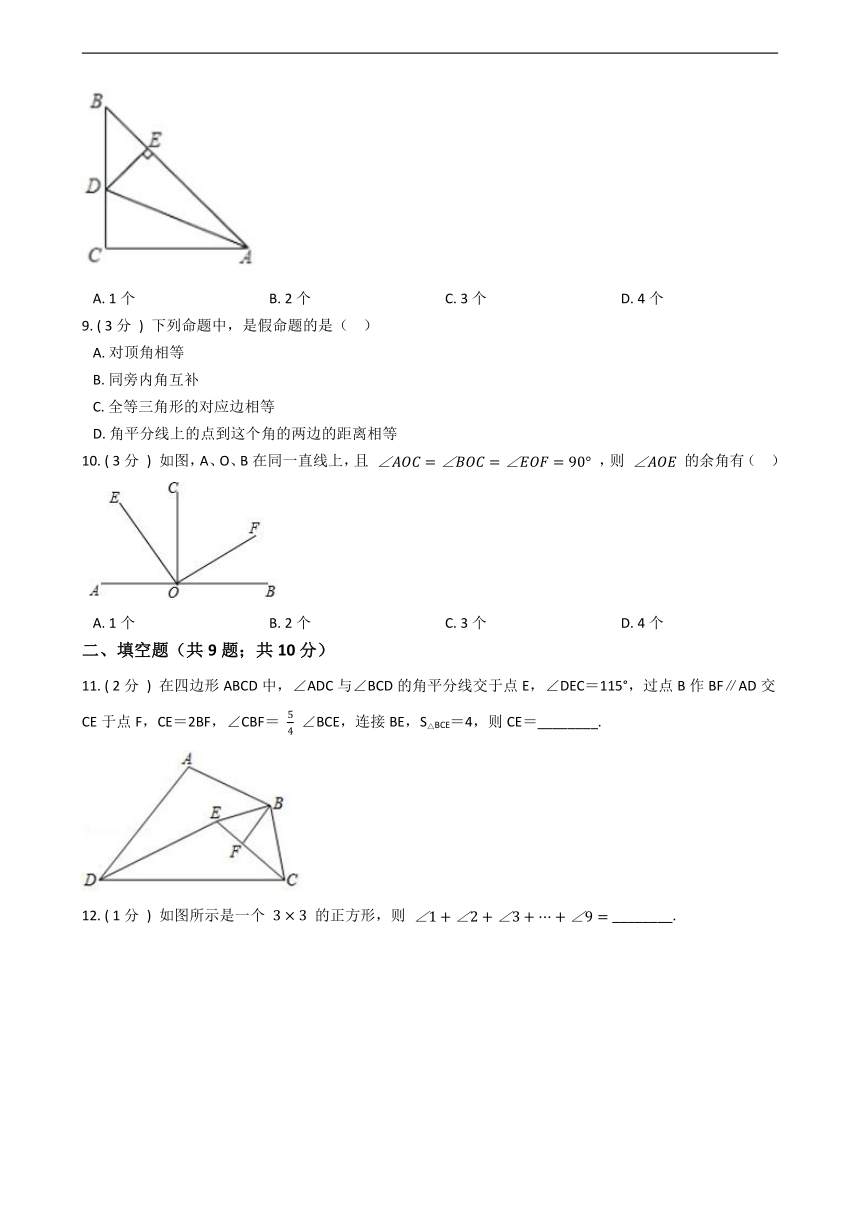
7. ( 3分 ) 如图所示,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2h后到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为(?????? )
A.?40海里???????????????????????????????B.?60海里???????????????????????????????C.?70海里???????????????????????????????D.?80海里
8. ( 3分 ) 如图所示,在△ABC中,∠C = 90°,AD平分∠BAC交BC于点D,DE⊥AB于点E,则下列结论:①AD平分∠CDE;②∠BAC = ∠BDE;③DE平分∠ADB;④若AC = 4BE,则S△ABC = 8S△BDE.其中正确的有(?? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
9. ( 3分 ) 下列命题中,是假命题的是(?? )
A.?对顶角相等
B.?同旁内角互补
C.?全等三角形的对应边相等
D.?角平分线上的点到这个角的两边的距离相等
10. ( 3分 ) 如图,A、O、B在同一直线上,且 ∠AOC=∠BOC=∠EOF=90° ,则 ∠AOE 的余角有(?? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题(共9题;共10分)
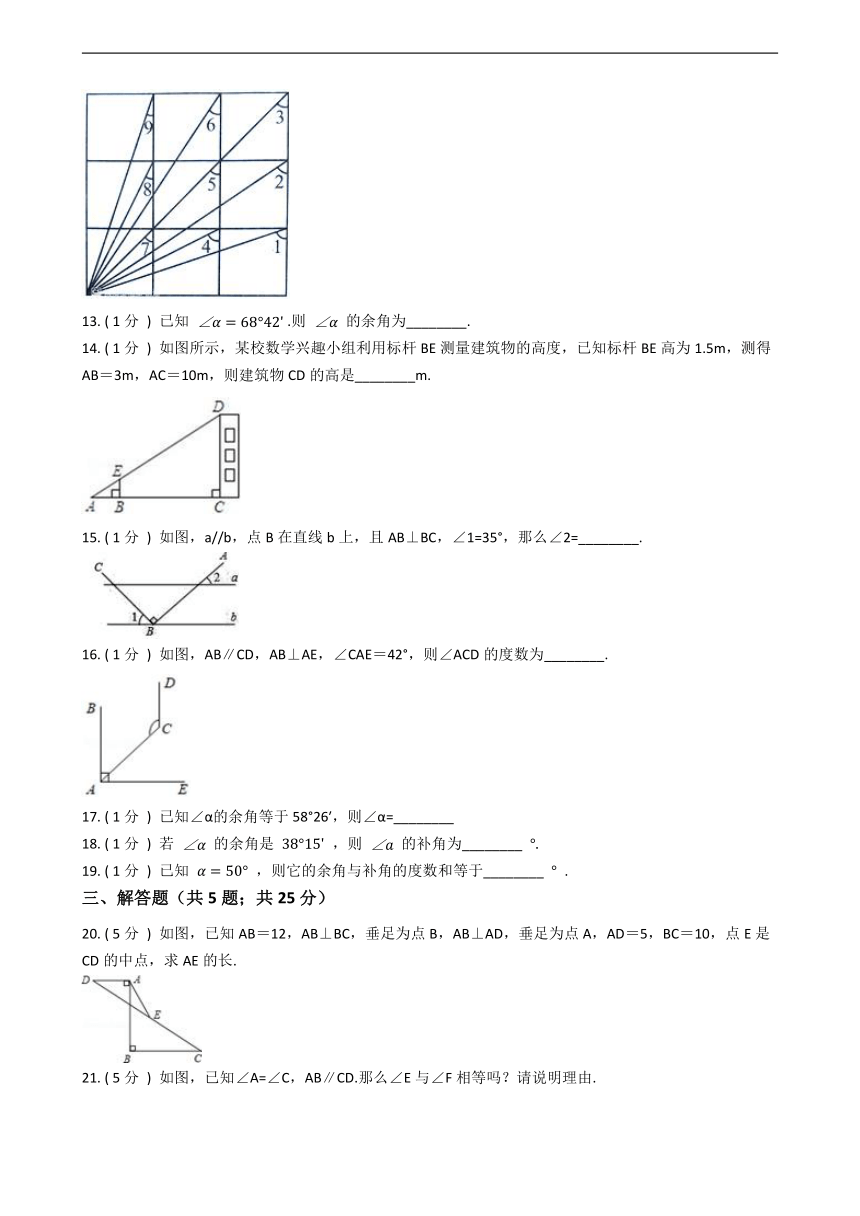
11. ( 2分 ) 在四边形ABCD中,∠ADC与∠BCD的角平分线交于点E,∠DEC=115°,过点B作BF∥AD交CE于点F,CE=2BF,∠CBF= 54 ∠BCE,连接BE,S△BCE=4,则CE=________.
12. ( 1分 ) 如图所示是一个 3×3 的正方形,则 ∠1+∠2+∠3+?+∠9= ________.
13. ( 1分 ) 已知 ∠α=68°42' .则 ∠α 的余角为________.
14. ( 1分 ) 如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高为1.5m,测得AB=3m,AC=10m,则建筑物CD的高是________m.
15. ( 1分 ) 如图,a//b,点B在直线b上,且AB⊥BC,∠1=35°,那么∠2=________.
16. ( 1分 ) 如图,AB∥CD,AB⊥AE,∠CAE=42°,则∠ACD的度数为________.
17. ( 1分 ) 已知∠α的余角等于58°26′,则∠α=________
18. ( 1分 ) 若 ∠α 的余角是 38°15' ,则 ∠a 的补角为________ °.
19. ( 1分 ) 已知 α=50° ,则它的余角与补角的度数和等于________ ° .
三、解答题(共5题;共25分)
20. ( 5分 ) 如图,已知AB=12,AB⊥BC,垂足为点B,AB⊥AD,垂足为点A,AD=5,BC=10,点E是CD的中点,求AE的长.
21. ( 5分 ) 如图,已知∠A=∠C,AB∥CD.那么∠E与∠F相等吗?请说明理由.
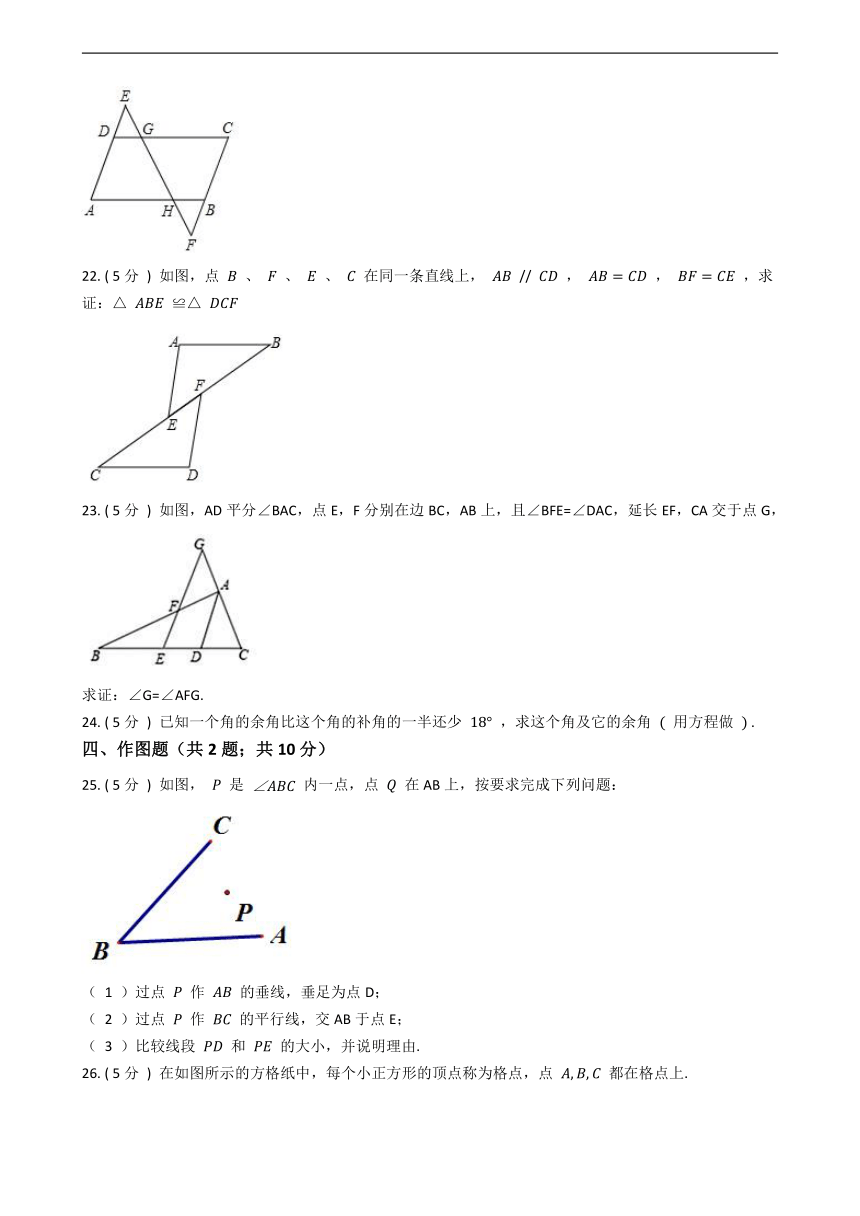
22. ( 5分 ) 如图,点 B 、 F 、 E 、 C 在同一条直线上, AB // CD , AB=CD , BF=CE ,求证:△ ABE ≌△ DCF
23. ( 5分 ) 如图,AD平分∠BAC,点E,F分别在边BC,AB上,且∠BFE=∠DAC,延长EF,CA交于点G,
求证:∠G=∠AFG.
24. ( 5分 ) 已知一个角的余角比这个角的补角的一半还少 18° ,求这个角及它的余角 ( 用方程做 ) .
四、作图题(共2题;共10分)
25. ( 5分 ) 如图, P 是 ∠ABC 内一点,点 Q 在AB上,按要求完成下列问题:
( 1 )过点 P 作 AB 的垂线,垂足为点D;
( 2 )过点 P 作 BC 的平行线,交AB于点E;
( 3 )比较线段 PD 和 PE 的大小,并说明理由.
26. ( 5分 ) 在如图所示的方格纸中,每个小正方形的顶点称为格点,点 A,B,C 都在格点上.
( 1 )找一格点 D ,使得直线 CD//AB ,画出直线 CD ;
( 2 )找一格点 E ,使得直线 AE⊥BC 于点 F ,画出直线 AE ,并注明垂足 F .
五、综合题(共4题;共45分)
27. ( 15分 ) 如图,在四边形 ABCD 中, ∠A=∠C=90° , DE , BF 分别平分 ∠ADC , ∠ABC ,并交线段 AB , CD 于点 E , F (点 E , B 不重合).在线段 BF 上取点 M , N (点 M 在 BN 之间),使 BM=2FN .当点 P 从点 D 匀速运动到点 E 时,点 Q 恰好从点 M 匀速运动到点 N .记 QN=x , PD=y ,已知 y=?65x+12 ,当 Q 为 BF 中点时, y=245 .
(1)判断 DE 与 BF 的位置关系,并说明理由.
(2)求 DE , BF 的长.
(3)若 AD=6 .
①当 DP=DF 时,通过计算比较 BE 与 BQ 的大小关系.
②连结 PQ ,当 PQ 所在直线经过四边形 ABCD 的一个顶点时,求所有满足条件的的值.
28. ( 10分 ) 如图,在四边形 ABCD 中, AE,BE 分别平分 ∠BAD 和 ∠ABC ,点 E 在 CD 上, ∠1+∠2=90°
(1)完成下面的说理过程解:
解: ∵AE平分∠BAD (已知),
∴∠BAD=2∠1 (???????????????? ),
∵BE平分∠ABC (已知),
∴∠ABC=2∠2 (???????????????? ),
∴∠BAD+∠ABC=2∠1+2∠2 (???????????????? ),
∵∠1+∠2=90° (已知),
∴∠BAD+∠ABC=180°
∴AD//BC (???????????????? ).
(2)若 AE 平分 ∠DEF ,试说明 BE 平分 ∠CEF .
29. ( 10分 ) 如图,已知 ∠AOC=2∠BOC , ∠AOC 的余角比 ∠BOC 小 30° .
?
(1)求 ∠AOB 的度数;
(2)过点O作射线OD,使得 ∠AOC=4∠AOD ,请你求出 ∠COD 的度数.
30. ( 10分 ) 如图,直线AB,CD相交于点O,OE平分 ∠BOC , ∠FOD=90°
(1)若 ∠AOF=50° ,求 ∠BOE 的度数;
(2)若 ∠BOD : ∠BOE=1 :4,求 ∠AOF 的度数.
答案解析部分
一、单选题
1.【答案】 A
【解析】【解答】解:如图,连接EC,CH,设AB交CR于点J.
∵四边形ACDE,四边形BCIH都是正方形,
∴∠ACE=∠BCH=45°.
∵DE∥AI∥BH,
∴∠CEP=∠CHQ.
∵∠ECP=∠HCQ,
∴△ECP∽△HCQ,
∴PCCQ=CECH=EPHQ=12.
∵PQ=15,
∴PC=5,CQ=10.
∵EC:CH=1:2,
∴AC:BC=1:2,设AC=a,BC=2a.
∵PQ⊥CR,?CR⊥AB,
∴CQ∥AB.
∵AC∥BQ,CQ∥AB,
∴四边形ABQC是平行四边形,
∴AB=CQ=10.
∵AC2+BC2=AB2 ,
∴5a2=100,
∴a=25 ,
∴AC=25 , BC=45.
∵12·AC·BC=12·AB·CJ,
∴CJ=25×4510=4.
∵JR=AF=AB=10,
∴CR=CJ+JR=14.
故答案为:A.
【分析】连接EC,CH.设AB交CR于J,利用正方形的性质,易证∠ACE=45°,∠ACB=∠BCI=90°,据此证明△ECP∽△HCQ,利用相似三角形对应边成比例可得PC、CQ的长,由EC:CH=1:2,推出AC:BC=1:2,设AC=a,BC=2a,证明四边形ABQC是平行四边形,推出AB=CQ=10,根据AC2+BC2=AB2 , 构建方程求出a即可解决问题.
2.【答案】 B
【解析】【解答】解:作PM⊥AC于点M,连接PD,则四边形AEPM为矩形,PE=AM.
∵DB=DC,
∴∠B=∠DCB.
∵PM⊥AC, AB⊥AC,
∴PM∥AB,
∴∠B=∠MPC,
∴∠DCB=∠MPC..
∵PC=PC,∠PFC=∠PMC=90°,∠DCB=∠MPC,
∴△PFC≌△CMP(AAS),
∴PF=CM,
∴PE+PF=AM+CM=AC.
∵AD:DB=1:3, 设AD=x,DB=3x,则CD=3x,AC=22x,BC=26x.
∵BC=46?,
∴x=2,
∴PE+PF=AC=22×2=42.
故答案为:B.
【分析】作PM⊥AC于点M,连接PD,可得矩形AEPM,易证△PFC≌△CMP,得到PE+PF=AC,然后设AD=x,表示出DB、CD、AC、BC,由BC=46?可得x的值,进而可求出PE+PF的值.
3.【答案】 D
【解析】【解答】解:∵∠BDC和∠BAC所对的弧都是BC弧,
∴∠BDC=∠BAC=40°,
∴∠ABE=180°-∠BAE-∠AEB=180°-40°-110°=30°,
∵BD为直径,
∴∠BCD=90°,
∴∠CBD=90°-∠BCD=90°-40°=50°,
∴∠ABC=∠ABD+∠CBD=30°+50°=80°,
故答案为:D.
【分析】根据圆周角定理,结合三角形内角和定理求出∠BAC的大小,然后根据直径所对的圆周角是直角,结合余角的性质求出∠CBD,最后根据角的和差关系求∠ABC即可.
4.【答案】 C
【解析】【解答】解: ?A、若?a//b,b//c? , ∵在同一平面内,平行于同一条直线的两条直线平行,则?a//c?,正确;
B、若∠1=∠2? , 利用内错角相等,两直线平行可得?a//c?,正确;
C、若∠2=∠3?,利用利用同位角相等,两直线平行可得?d∥e??,错误;
D、若?∠1+∠5=180°? , 利用同旁内角互补,两直线平行可得d//e , 正确;
故答案为:C.
【分析】在同一平面内,平行于同一条直线的两条直线平行,对A作出判断;分别根据平行线的性质定理可得BCD作出判断.
5.【答案】 B
【解析】【解答】∵AD∥BC,
∴∠ABC+∠BAD=180°,且∠ABC=58°,
∴∠BAD=122°,
∵将右侧部分纸片四边形ABCD沿线段AB翻折至四边形ABC'D',
∴∠BAD=∠BAD'=122°,
∴∠1=122°-58°=64°,
故答案为:B.
【分析】由平行线的性质可得∠BAD=122°,由折叠的性质可得∠BAD=∠BAD'=122°,即可求解.
6.【答案】 B
【解析】【解答】解:①若两条直线相交所形成的四个角中有三个角相等,则这两条直线互相垂直,该说法正确;
②若点C在线段AB上,且 AC=BC ,则 C 是线段 AB 的中点,原说法错误;
③在同一平面内,不相交的两条直线必平行,原说法错误;
④两点确定一条直线,此说法正确.
故答案为:B.
【分析】根据平行线的定义、垂线的定义、相交线的定义、两点确定一条直线,对各个小题分析判断即可得解.
7.【答案】 D
【解析】【解答】解:由题意可得:MN=2×40=80(海里),∠M=70°,∠N=40°,
∴∠MPN=180°-∠M-∠N=180°-70°-40°=70°,
∴∠M=∠MPN,
∴NP=MN=80(海里).
故答案为:D.
【分析】首先由速度以及时间求出MN的值,然后根据两直线平行,内错角相等可得到∠N、∠M的度数,进一步推出∠M=∠MPN,最后结合等腰三角形的判定解答即可.
8.【答案】 B
【解析】【解答】解:∵ AD平分∠BAC,
∴∠DAC=∠DAE.
∵∠C=90°, DE⊥AB,
∴∠C=∠E=90°.
∵AD=AD,∠DAC=∠DAE,∠C=∠E=90°,
∴△DAC≌△DAE,
∴∠CDA=∠EDA,
∴① AD平分∠CDE ,正确.
无法证明∠BDE=60°,
∴③ DE平分∠ADB错误.
∵BE+AE=AB,AE=AC,AC=4BE,
∴AB=5BE,AE=4BE,
∴S△ADB=5S△BDE , S△ADC=4S△BDE ,
∴S△ABC=9S△BDE , ④错误.
∵∠BDE=90°-∠B,∠BAC=90°-∠B,
∴∠BDE=∠BAC,
∴②∠BAC=∠BDE正确.
故答案为:B.
【分析】根据角平分线的概念以及性质可得∠DAC=∠DAE,∠C=∠E=90°,然后可证△DAC≌△DAE,根据全等三角形的性质可判断①的正误;无法推出∠BDE=60°,进而可判断③的正误;由线段的和差关系可推出AB=5BE,AE=4BE,利用三角形的面积公式不难判断④的正误;根据同角的余角相等可判断②的正误.
9.【答案】 B
【解析】【解答】解:A、对顶角相等是真命题,故A不符合题意;
B、同旁内角互补是假命题,故B符合题意;
C、全等三角形的对应边相等是真命题,故C不符合题意;
D、角平分线上的点到这个角的两边的距离相等.是真命题,故D不符合题意;、
故答案为:B.
【分析】利用对顶角的性质,可对A作出判断;利用两直线平行,同旁内角互补,可对B作出判断;利用全等三角形的性质,可对C作出判断;利用角平分线的性质,可对D作出判断,由此可得到是假命题的选项.
10.【答案】 B
【解析】【解答】解: ∵∠AOC=90° ,
∴∠COE+∠AOE=90° ,
即 ∠AOE 的余角是 ∠COE ;
又 ∵∠EOF=90° , ∠AOB=180° ,
∴∠BOF+∠AOE=90° ,
即 ∠AOE 的余角是 ∠BOF .
故答案为:B
【分析】根据互余的定义,即是求与 ∠AOE 的和是 90° 的角,根据角相互间的和差关系可得.本题主要考查了平角,余角的定义,是一个基本的类型,熟记定义是关键.
二、填空题
11.【答案】 4
【解析】【解答】解:∵DE平分∠ADC,CE平分∠DCB,
∴∠ADE=∠EDC,∠ECD=∠ECB.
∵AD∥BF,
∴∠A+∠ABF=180°,
∴∠ADC+∠DCB+∠CBF=180°,
∴2∠EDC+2∠BCE+54∠BCE=180°.
∵∠DEC=115°,
∴∠EDC+∠ECD=65°,
∴∠EDC+∠BCE=65°,
∴∠BCE=40°,∠EDC=25°,
∴∠CBF=54∠BCE=50°,
∴∠CFB=90°,
∴BF⊥EC,
∴CE=2BF,设BF=m,则CE=2m.
∵S△BCE=?12EC·BF=4,
∴12×2m×m=4,
∴m=2或-2(舍去),
∴CE=2m=4.
故答案为:4.
【分析】由AD∥BF,可得∠A+∠ABF=180°,进而由四边形内角和为360°可得∠ADC+∠DCB+∠BCE=180°,由∠DEC=115°,可得∠EDC+∠DCE=65°,然后结合角平分线的概念可求得∠BCE、∠EDC、∠CBF的度数,然后求出∠CFB=90°,再利用三角形的面积公式求解即可.
12.【答案】 405°
【解析】【解答】解:根据正方形的性质和全等三角形的性质可知,
∠1+∠9=90°,∠2+∠6=90°,∠3=∠5=∠7=45°,∠4+∠8=90°,
∴ ∠1+∠2+∠3+?+∠9=3×90°+3×45°=405°?,
故答案为:405°.
【分析】根据正方形的性质和全等三角形的性质分析,找出互余的三对角,结合等腰直角三角形的性质即可求出这几个角的和.
13.【答案】 21°18′
【解析】【解答】解: ∵ ∠α=68°42'
∴ ∠α 的余角为 90°?68°42′=89°60′?68°42′=21°18′
故答案为:21°18′.
【分析】根据互为余角的两个角的和等于90°,列式计算即可.
14.【答案】 5
【解析】【解答】解:∵EB⊥AC,CD⊥AC,
∴EB∥CD,
∴△AEB∽△ADC,
∴BEAB=CDAC ,
∴1.53=CD10 ,
∴CD=5.
故答案为:5.
【分析】根据垂直于同一直线的两直线互相平行可得EB∥CD,进而推出△AEB∽△ADC,然后借助相似三角形对应边成比例就可求得CD的值.
15.【答案】 55°
【解析】【解答】解:如图,
∵AB⊥BC,∴∠3=90°﹣∠1=55°.
∵a∥b,∴∠2=∠3=55°.
故答案为:55°.
【分析】根据垂直的定义及平角的定义,可求得∠3=55°,根据两直线平行同位角相等可得∠2=∠3=55°.
16.【答案】 132°
【解析】【解答】解:∵AB⊥AE,
∴∠BAC+∠CAE=90°
∴∠BAC=90°-42°=48°,
∵AB∥CD,
∴∠ACD+∠BAC=180°,
∴∠ACD=180°-48°=132°.
故答案为:132°.
【分析】利用垂直的定义可证得∠BAC+∠CAE=90°,由此可求出∠BAC的度数;再利用两直线平行,同旁内角互补,就可求出∠ACD的度数.
17.【答案】 31°34′
【解析】【解答】解:由余角的定义得:∠α=90°﹣58°26′=31°34′,
故答案为:31°34′.
【分析】根据和为90°的两个角就互为余角即可得出答案.
18.【答案】 128.25
【解析】【解答】解: ∵∠α 的余角是 38°15' ,
∴∠a 的补角为: 38°15'+90°=128.25° .
故答案为:128.25.
【分析】根据同角的补角比余角大90°即可求出答案.
19.【答案】 170
【解析】【解答】解: ∵α=50° ,
∴ 根据互为补角的概念,得
α 的补角为: 180°?50°=130° ,
根据互为余角的概念,得,
α 的余角为: 90°?50°=40° ,
∴ 余角与补角的度数和为: 130°+40°=170° .
故答案为170.
【分析】此题考查余角和补角的概念,如果两个角的和等于 180°( 平角 ) ,就说这两个角互为补角.如果两个角和为 90° ,则两个角互为余角.根据概念先求出 α 的余角和补角,再进行相加计算即可.
三、解答题
20.【答案】 解:如图,延长AE交BC于点F,
∵点E是CD的中点 ∴DE=CE,
∵AB⊥BC,AB⊥AD ∴AD∥BC
∴∠ADE=∠BCE且DE=CE,∠AED=∠CEF
∴△AED≌△FEC(ASA)
∴AD=FC=5,AE=EF
∴BF=BC﹣FC=5
∴在Rt△ABF中,AF= AB2+BF2 =13
∴AE= AF2 = 132
【解析】【分析】 延长AE交BC于点F,易证△AED≌△FEC,然后由全等三角形对应边相等可求出AD、FC、BF的值,接下来在Rt△ABF中,根据勾股定理可得AF的值,最后根据AE=EF就可得到AE的值.
21.【答案】 解:∠E=∠F.理由如下:
∵AB∥CD,
∴∠A=∠EDC.
∵∠A=∠C,
∴∠EDC=∠C,
∴AE∥CF,
∴∠E=∠F.
【解析】【分析】由AB∥CD,根据平行线的性质得∠A=∠EDC,而∠A=∠C,则∠EDC=∠C,根据平行线的判定得到AE∥CF,然后再根据平行线的性质得到∠E=∠F.
22.【答案】 解: ∵AB//CD (已知),
∴∠B=∠C (两直线平行,内错角相等)
∵BF=CE (已知),
∴BF+EF=CE+EF ,即 BE=CF .
在 ΔABE 和 ΔDCF 中,
{AB=CD∠B=∠CBE=CF ,
∴ΔABE?ΔDCF(SAS)
【解析】【分析】?根据两直线平行,内错角相等,可得∠B=∠C,由BF=CE得出BE=CF,根据SAS可证△ABE≌△DCF.
23.【答案】 证明:∵AD平分∠BAC,
∴∠DAB=∠DAC
∵∠BFE=∠DAC,
∴∠BFE=∠DAB,
∴AD∥EG,
∴∠G=∠DAC
又∵∠BFE=∠DAC,
∴∠G=∠BFE,
由对顶角相等得:∠BFE=∠AFG,
∴∠G=∠AFG.
【解析】【分析】利用角平分线的定义可得到∠DAB=∠DAC,结合已知可推出∠BFE=∠DAB;再利用两直线平行同位角相等可证得∠G=∠DAC,由此可得到∠G=∠BFE,然后可证得结论.
24.【答案】 解:设这个角是 α ,则它的余角为 90°?α ,补角为 180°?α ,
由题意得, 90°?α=12(180°?α)?18° ,
解得 α=36° ,
90°?36°=54° .
答:这个角是 36° ,它的余角是 54°
【解析】【分析】设这个角是 α ,然后表示出它的余角和补角,再列出方程求解即可.
四、作图题
25.【答案】 解:所以如图为所求做图形.
PE>PD
理由:点到直线垂线段最短.
【解析】【分析】 (1)根据垂线的定义即可过点P画AB的垂线,垂足为点D;
(2)根据平行线的定义即可过点P画BC的平行线交AB于点E;
(3)由垂线段最短可知PE>PD.
26.【答案】 解:直线CD\AE,点F如图所示;
【解析】【分析】(1)根据直线的定义,平行线的定义画出图形即可.(2)根据直线的定义,垂线的定义画出图形即可.
五、综合题
27.【答案】 (1)解: DE 与 BF 的位置关系为: DE//BF ,理由如下:
如图1所示:
∵∠A=∠C=90° , ∴∠ADC+∠ABC=360°?(∠A+∠C)=180° ,
∵DE 、 BF 分别平分 ∠ADC 、 ∠ABC , ∴∠ADE=12∠ADC , ∠ABF=12∠ABC ,
∴∠ADE+∠ABF=12×180°=90° ,
∵∠ADE+∠AED=90° , ∴∠AED=∠ABF , ∴DE//BF ;
(2)解:令 x=0 ,得 y=12 , ∴DE=12 ,
令 y=0 ,得 x=10 , ∴MN=10 ,
把 y=245 代入 y=?65x+12 ,
解得: x=6 ,即 NQ=6 , ∴QM=10?6=4 ,
∵Q 是 BF 中点, ∴FQ=QB ,
∵BM=2FN , ∴FN+6=4+2FN ,
解得: FN=2 , ∴BM=4 , ∴BF=FN+MN+MB=16 ;
(3)解:①连接 EM 并延长交 BC 于点 H ,如图2所示:
∵FM=2+10=12=DE , DE//BF ,四边形 DFME 是平行四边形, ∴DF=EM ,
∵AD=6 , DE=12 , ∠A=90° , ∴∠DEA=30° , ∴∠DEA=∠FBE=∠FBC=30° ,
∴∠ADE=60° , ∴∠ADE=∠CDE=∠FME=60° ,
∴∠DFM=∠DEM=120° , ∴∠MEB=180°?120°?30°=30° ,
∴∠MEB=∠FBE=30° , ∴∠EHB=180°?30°?30°?30°=90° , DF=EM=BM=4 ,
∴MH=12BM=2 , ∴EH=4+2=6 ,
由勾股定理得: HB=BM2?MH2=42?22=23 ,
∴BE=EH2?HB2=62+(23)2=43 ,
当 DP=DF 时, ?65x+12=4 ,解得: x=203 ,
∴BQ=14?x=14?203=223 ,
223>43 , ∴BQ>BE ;
②(Ⅰ)当 PQ 经过点 D 时,如图3所示:
y=0 ,则 x=10 ;
(Ⅱ)当 PQ 经过点 C 时,如图4所示:
∵BF=16 , ∠FCB=90° , ∠CBF=30° , ∴CF=12BF=8 , ∴CD=8+4=12 ,
∵FQ//DP , ∴ΔCFQ∽ΔCDP , FQDP=CFCD , 2+x?65x+12=812 ,解得: x=103 ;
(Ⅲ)当 PQ 经过点 A 时,如图5所示:
∵PE//BQ , ∴ΔAPE∽ΔAQB , PEBQ=AEAB ,
由勾股定理得: AE=DE2?AD2=122?62=63 ,
∴AB=63+43=103 , 12?(?65x+12)14?x=63103 ,
解得: x=143 ,
由图可知, PQ 不可能过点 B ;
综上所述,当 x=10 或 x=103 或 x=143 时, PQ 所在的直线经过四边形 ABCD 的一个顶点.
【解析】【分析】(1)首先由四边形内角和为360°可得∠ADC+∠ABC=180°,然后根据角平分线的定义可得∠ADE+∠ABF的度数,结合∠ADE+∠AED=90°可得∠AED与∠ABF的数量关系,进而判断DE与BF的位置关系;
(2)分别令x=0、y=0求出对应的y、x的值,即为DE、MN的值,把y=245代入求出x的值,即为NQ的值,然后根据QM=MN-NQ求出QM的值,由Q为BF的中点以及BM=2FN可得到关于FN的等式,进而求出FN的值,最后根据BF=FN+MN+MB计算即可;
(3)①连接EM并延长交BC于点H,可推出四边形DFME为平行四边形,由平行四边形的性质以及平行线的性质可求得∠DEA,∠ADE,∠DFM,∠MEB,∠EHB的度数,进一步得到MH、EH的值,然后利用勾股定理求出HB、BE的值,利用DP=DF可得关于x的方程,求解即可;
②当PQ经过点C时,首先求出CF、CD的值,由△CFQ∽△CDP可得关于x的方程,求解即可;当PQ经过点A时,易证△APE∽△AQB,由勾股定理求出AE的值,进而得到AB的值,然后利用相似三角形对应边成比例可得关于x的方程,求解即可.
28.【答案】 (1)解: ∵AE平分∠BAD (已知),
∴∠BAD=2∠1 (角平分线的定义? ),
∵BE平分∠ABC (已知),
∴∠ABC=2∠2 (角平分线的定义? ),
∴∠BAD+∠ABC=2∠1+2∠2 (??? 等量代换????? ),
∵∠1+∠2=90° (已知),
∴∠BAD+∠ABC=180°
∴AD//BC (? 同旁内角互补,两直线平行? ).
(2)解: ∵∠1+∠2+∠AEB=180°,∠1+∠2=90°
∴∠AEB=90°=∠AEF+∠BEF
∵∠AED+∠AEB+∠CEB=180°
∴∠AED+∠CEB=90°
∵AE 平分 ∠DEF
∴∠AED=∠AEF
∴∠BEF=∠CEB (等角的余角相等)
∴BE 平分 ∠CEF
【解析】【分析】(1)首先根据角平分线定义可得∠BAD=2∠1,∠ABC=2∠2,则由等量代换可得∠BAD+∠ABC=2∠1+2∠2,根据同旁内角互补,两直线平行可得AD∥BC;
(2)由三角形内角和定理,结合∠1和∠2互余可得∠AEB为90°,从而得出∠AED和∠BEC互余,则由AE平分∠DEF,根据余角的性质得出BE平分∠CEF.
29.【答案】 (1)解:设 ∠BOC=x ,则 ∠AOC=2x ,
依题意列方程 90°?2x=x?30° ,
解得: x=40° ,
即 ∠AOB=40°
(2)解:由 (1) 得, ∠AOC=80° ,
①当射线OD在 ∠AOC 内部时, ∠AOD=20° ,
则 ∠COD=∠AOC?∠AOD=60° ;
②当射线OD在 ∠AOC 外部时, ∠AOD=20° ,
则 ∠COD=∠AOC+∠AOD=100° .
【解析】【分析】(1)设 ∠BOC=x ,则 ∠AOC=2x ,根据∠AOC 的余角比 ∠BOC 小 30゜ 列方程求解即可;
(2)分两种情况:①当射线OD在 ∠AOC内部,②当射线OD在 ∠AOC 外部,分别求出 ∠COD 的度数即可.
30.【答案】 (1)解: ∵∠COF 与 ∠DOF 是邻补角,
∴∠COF=180°?∠DOF=90° .
∵∠AOC 与 ∠AOF 互为余角,
∴∠AOC=90°?∠AOF=90°?50°=40° .
∵∠AOC 与 ∠BOC 是邻补角,
∴∠COB=180°?∠AOC=180°?40°=140° .
∵OE 平分 ∠BOC ,
∴∠BOE=12∠BOC=70°
(2)解: ∠BOD : ∠BOE=1 :4,
设 ∠BOD=∠AOC=x , ∠BOE=∠COE=4x .
∵∠AOC 与 ∠BOC 是邻补角,
∴∠AOC+∠BOC=180° ,
即 x+4x+4x=180° ,
解得 x=20° .
∵∠AOC 与 ∠AOF 互为余角,
∴∠AOF=90°?∠AOC=90°?20°=70°
【解析】【分析】(1)根据补角,余角的关系,可得 ∠COB ,根据角平分线的定义,可得答案;
(2)根据邻补角,可得关于x的方程,解方程可得 ∠AOC ,再根据余角的定义,可得答案.
考试时间:120分钟 满分:120分
姓名:__________ 班级:__________考号:__________
一、单选题(共10题;共30分)
1. ( 3分 ) 如图,在 RtΔABC 中, ∠ACB=90° ,以其三边为边向外作正方形,过点 C 作 CR⊥FG 于点 R ,再过点 C 作 PQ⊥CR 分别交边 DE , BH 于点 P , Q .若 QH=2PE , PQ=15 ,则 CR 的长为 ( ?? )
A.?14???????????????????????????????????????B.?15???????????????????????????????????????C.?83???????????????????????????????????????D.?65
2. ( 3分 ) 如图,在△ABC中,∠A=90°,P是BC上一点,且DB=DC,过BC上一点P,作PE⊥AB于E,PF⊥DC于F,已知:AD:DB=1:3,BC= 46 ,则PE+PF的长是(?? )
A.?46??????????????????????????????????????B.?42??????????????????????????????????????C.?6??????????????????????????????????????D.?26
3. ( 3分 ) 如图,四边形ABCD内接于?O,连结对角线AC与BD交于点E,且BD为?O的直径,已知∠BDC=40°,∠AEB=110°,则∠ABC=(???? )
A.?65°???????????????????????????????????????B.?70°???????????????????????????????????????C.?75°???????????????????????????????????????D.?80°
4. ( 3分 ) 如图,下列说法错误的是(? )
A.?若 a//b,b//c ,则 a//c?????????????????????????????????B.?若 ∠1=∠2 ,则 a//c
C.?若 ∠2=∠3 ,则 b//c???????????????????????????????????D.?若 ∠1+∠5=180° ,则 d//e
5. ( 3分 ) 如图,在一张长方形纸片上画一条线段AB,将右侧部分纸片四边形ABCD沿线段AB翻折至四边形ABC'D',若∠ABC=58°,则∠1=(?? )
A.?60°???????????????????????????????????????B.?64°???????????????????????????????????????C.?42°???????????????????????????????????????D.?52°
6. ( 3分 ) 下列说法中:
①若两条直线相交所形成的四个角中有三个角相等,则这两条直线互相垂直;②若 AC=BC ,则 C 是线段 AB 的中点;③在同一平面内,不相交的两条线段必平行;④两点确定一条直线.其中说法正确的个数(?? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
7. ( 3分 ) 如图所示,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2h后到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为(?????? )
A.?40海里???????????????????????????????B.?60海里???????????????????????????????C.?70海里???????????????????????????????D.?80海里
8. ( 3分 ) 如图所示,在△ABC中,∠C = 90°,AD平分∠BAC交BC于点D,DE⊥AB于点E,则下列结论:①AD平分∠CDE;②∠BAC = ∠BDE;③DE平分∠ADB;④若AC = 4BE,则S△ABC = 8S△BDE.其中正确的有(?? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
9. ( 3分 ) 下列命题中,是假命题的是(?? )
A.?对顶角相等
B.?同旁内角互补
C.?全等三角形的对应边相等
D.?角平分线上的点到这个角的两边的距离相等
10. ( 3分 ) 如图,A、O、B在同一直线上,且 ∠AOC=∠BOC=∠EOF=90° ,则 ∠AOE 的余角有(?? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题(共9题;共10分)
11. ( 2分 ) 在四边形ABCD中,∠ADC与∠BCD的角平分线交于点E,∠DEC=115°,过点B作BF∥AD交CE于点F,CE=2BF,∠CBF= 54 ∠BCE,连接BE,S△BCE=4,则CE=________.
12. ( 1分 ) 如图所示是一个 3×3 的正方形,则 ∠1+∠2+∠3+?+∠9= ________.
13. ( 1分 ) 已知 ∠α=68°42' .则 ∠α 的余角为________.
14. ( 1分 ) 如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高为1.5m,测得AB=3m,AC=10m,则建筑物CD的高是________m.
15. ( 1分 ) 如图,a//b,点B在直线b上,且AB⊥BC,∠1=35°,那么∠2=________.
16. ( 1分 ) 如图,AB∥CD,AB⊥AE,∠CAE=42°,则∠ACD的度数为________.
17. ( 1分 ) 已知∠α的余角等于58°26′,则∠α=________
18. ( 1分 ) 若 ∠α 的余角是 38°15' ,则 ∠a 的补角为________ °.
19. ( 1分 ) 已知 α=50° ,则它的余角与补角的度数和等于________ ° .
三、解答题(共5题;共25分)
20. ( 5分 ) 如图,已知AB=12,AB⊥BC,垂足为点B,AB⊥AD,垂足为点A,AD=5,BC=10,点E是CD的中点,求AE的长.
21. ( 5分 ) 如图,已知∠A=∠C,AB∥CD.那么∠E与∠F相等吗?请说明理由.
22. ( 5分 ) 如图,点 B 、 F 、 E 、 C 在同一条直线上, AB // CD , AB=CD , BF=CE ,求证:△ ABE ≌△ DCF
23. ( 5分 ) 如图,AD平分∠BAC,点E,F分别在边BC,AB上,且∠BFE=∠DAC,延长EF,CA交于点G,
求证:∠G=∠AFG.
24. ( 5分 ) 已知一个角的余角比这个角的补角的一半还少 18° ,求这个角及它的余角 ( 用方程做 ) .
四、作图题(共2题;共10分)
25. ( 5分 ) 如图, P 是 ∠ABC 内一点,点 Q 在AB上,按要求完成下列问题:
( 1 )过点 P 作 AB 的垂线,垂足为点D;
( 2 )过点 P 作 BC 的平行线,交AB于点E;
( 3 )比较线段 PD 和 PE 的大小,并说明理由.
26. ( 5分 ) 在如图所示的方格纸中,每个小正方形的顶点称为格点,点 A,B,C 都在格点上.
( 1 )找一格点 D ,使得直线 CD//AB ,画出直线 CD ;
( 2 )找一格点 E ,使得直线 AE⊥BC 于点 F ,画出直线 AE ,并注明垂足 F .
五、综合题(共4题;共45分)
27. ( 15分 ) 如图,在四边形 ABCD 中, ∠A=∠C=90° , DE , BF 分别平分 ∠ADC , ∠ABC ,并交线段 AB , CD 于点 E , F (点 E , B 不重合).在线段 BF 上取点 M , N (点 M 在 BN 之间),使 BM=2FN .当点 P 从点 D 匀速运动到点 E 时,点 Q 恰好从点 M 匀速运动到点 N .记 QN=x , PD=y ,已知 y=?65x+12 ,当 Q 为 BF 中点时, y=245 .
(1)判断 DE 与 BF 的位置关系,并说明理由.
(2)求 DE , BF 的长.
(3)若 AD=6 .
①当 DP=DF 时,通过计算比较 BE 与 BQ 的大小关系.
②连结 PQ ,当 PQ 所在直线经过四边形 ABCD 的一个顶点时,求所有满足条件的的值.
28. ( 10分 ) 如图,在四边形 ABCD 中, AE,BE 分别平分 ∠BAD 和 ∠ABC ,点 E 在 CD 上, ∠1+∠2=90°
(1)完成下面的说理过程解:
解: ∵AE平分∠BAD (已知),
∴∠BAD=2∠1 (???????????????? ),
∵BE平分∠ABC (已知),
∴∠ABC=2∠2 (???????????????? ),
∴∠BAD+∠ABC=2∠1+2∠2 (???????????????? ),
∵∠1+∠2=90° (已知),
∴∠BAD+∠ABC=180°
∴AD//BC (???????????????? ).
(2)若 AE 平分 ∠DEF ,试说明 BE 平分 ∠CEF .
29. ( 10分 ) 如图,已知 ∠AOC=2∠BOC , ∠AOC 的余角比 ∠BOC 小 30° .
?
(1)求 ∠AOB 的度数;
(2)过点O作射线OD,使得 ∠AOC=4∠AOD ,请你求出 ∠COD 的度数.
30. ( 10分 ) 如图,直线AB,CD相交于点O,OE平分 ∠BOC , ∠FOD=90°
(1)若 ∠AOF=50° ,求 ∠BOE 的度数;
(2)若 ∠BOD : ∠BOE=1 :4,求 ∠AOF 的度数.
答案解析部分
一、单选题
1.【答案】 A
【解析】【解答】解:如图,连接EC,CH,设AB交CR于点J.
∵四边形ACDE,四边形BCIH都是正方形,
∴∠ACE=∠BCH=45°.
∵DE∥AI∥BH,
∴∠CEP=∠CHQ.
∵∠ECP=∠HCQ,
∴△ECP∽△HCQ,
∴PCCQ=CECH=EPHQ=12.
∵PQ=15,
∴PC=5,CQ=10.
∵EC:CH=1:2,
∴AC:BC=1:2,设AC=a,BC=2a.
∵PQ⊥CR,?CR⊥AB,
∴CQ∥AB.
∵AC∥BQ,CQ∥AB,
∴四边形ABQC是平行四边形,
∴AB=CQ=10.
∵AC2+BC2=AB2 ,
∴5a2=100,
∴a=25 ,
∴AC=25 , BC=45.
∵12·AC·BC=12·AB·CJ,
∴CJ=25×4510=4.
∵JR=AF=AB=10,
∴CR=CJ+JR=14.
故答案为:A.
【分析】连接EC,CH.设AB交CR于J,利用正方形的性质,易证∠ACE=45°,∠ACB=∠BCI=90°,据此证明△ECP∽△HCQ,利用相似三角形对应边成比例可得PC、CQ的长,由EC:CH=1:2,推出AC:BC=1:2,设AC=a,BC=2a,证明四边形ABQC是平行四边形,推出AB=CQ=10,根据AC2+BC2=AB2 , 构建方程求出a即可解决问题.
2.【答案】 B
【解析】【解答】解:作PM⊥AC于点M,连接PD,则四边形AEPM为矩形,PE=AM.
∵DB=DC,
∴∠B=∠DCB.
∵PM⊥AC, AB⊥AC,
∴PM∥AB,
∴∠B=∠MPC,
∴∠DCB=∠MPC..
∵PC=PC,∠PFC=∠PMC=90°,∠DCB=∠MPC,
∴△PFC≌△CMP(AAS),
∴PF=CM,
∴PE+PF=AM+CM=AC.
∵AD:DB=1:3, 设AD=x,DB=3x,则CD=3x,AC=22x,BC=26x.
∵BC=46?,
∴x=2,
∴PE+PF=AC=22×2=42.
故答案为:B.
【分析】作PM⊥AC于点M,连接PD,可得矩形AEPM,易证△PFC≌△CMP,得到PE+PF=AC,然后设AD=x,表示出DB、CD、AC、BC,由BC=46?可得x的值,进而可求出PE+PF的值.
3.【答案】 D
【解析】【解答】解:∵∠BDC和∠BAC所对的弧都是BC弧,
∴∠BDC=∠BAC=40°,
∴∠ABE=180°-∠BAE-∠AEB=180°-40°-110°=30°,
∵BD为直径,
∴∠BCD=90°,
∴∠CBD=90°-∠BCD=90°-40°=50°,
∴∠ABC=∠ABD+∠CBD=30°+50°=80°,
故答案为:D.
【分析】根据圆周角定理,结合三角形内角和定理求出∠BAC的大小,然后根据直径所对的圆周角是直角,结合余角的性质求出∠CBD,最后根据角的和差关系求∠ABC即可.
4.【答案】 C
【解析】【解答】解: ?A、若?a//b,b//c? , ∵在同一平面内,平行于同一条直线的两条直线平行,则?a//c?,正确;
B、若∠1=∠2? , 利用内错角相等,两直线平行可得?a//c?,正确;
C、若∠2=∠3?,利用利用同位角相等,两直线平行可得?d∥e??,错误;
D、若?∠1+∠5=180°? , 利用同旁内角互补,两直线平行可得d//e , 正确;
故答案为:C.
【分析】在同一平面内,平行于同一条直线的两条直线平行,对A作出判断;分别根据平行线的性质定理可得BCD作出判断.
5.【答案】 B
【解析】【解答】∵AD∥BC,
∴∠ABC+∠BAD=180°,且∠ABC=58°,
∴∠BAD=122°,
∵将右侧部分纸片四边形ABCD沿线段AB翻折至四边形ABC'D',
∴∠BAD=∠BAD'=122°,
∴∠1=122°-58°=64°,
故答案为:B.
【分析】由平行线的性质可得∠BAD=122°,由折叠的性质可得∠BAD=∠BAD'=122°,即可求解.
6.【答案】 B
【解析】【解答】解:①若两条直线相交所形成的四个角中有三个角相等,则这两条直线互相垂直,该说法正确;
②若点C在线段AB上,且 AC=BC ,则 C 是线段 AB 的中点,原说法错误;
③在同一平面内,不相交的两条直线必平行,原说法错误;
④两点确定一条直线,此说法正确.
故答案为:B.
【分析】根据平行线的定义、垂线的定义、相交线的定义、两点确定一条直线,对各个小题分析判断即可得解.
7.【答案】 D
【解析】【解答】解:由题意可得:MN=2×40=80(海里),∠M=70°,∠N=40°,
∴∠MPN=180°-∠M-∠N=180°-70°-40°=70°,
∴∠M=∠MPN,
∴NP=MN=80(海里).
故答案为:D.
【分析】首先由速度以及时间求出MN的值,然后根据两直线平行,内错角相等可得到∠N、∠M的度数,进一步推出∠M=∠MPN,最后结合等腰三角形的判定解答即可.
8.【答案】 B
【解析】【解答】解:∵ AD平分∠BAC,
∴∠DAC=∠DAE.
∵∠C=90°, DE⊥AB,
∴∠C=∠E=90°.
∵AD=AD,∠DAC=∠DAE,∠C=∠E=90°,
∴△DAC≌△DAE,
∴∠CDA=∠EDA,
∴① AD平分∠CDE ,正确.
无法证明∠BDE=60°,
∴③ DE平分∠ADB错误.
∵BE+AE=AB,AE=AC,AC=4BE,
∴AB=5BE,AE=4BE,
∴S△ADB=5S△BDE , S△ADC=4S△BDE ,
∴S△ABC=9S△BDE , ④错误.
∵∠BDE=90°-∠B,∠BAC=90°-∠B,
∴∠BDE=∠BAC,
∴②∠BAC=∠BDE正确.
故答案为:B.
【分析】根据角平分线的概念以及性质可得∠DAC=∠DAE,∠C=∠E=90°,然后可证△DAC≌△DAE,根据全等三角形的性质可判断①的正误;无法推出∠BDE=60°,进而可判断③的正误;由线段的和差关系可推出AB=5BE,AE=4BE,利用三角形的面积公式不难判断④的正误;根据同角的余角相等可判断②的正误.
9.【答案】 B
【解析】【解答】解:A、对顶角相等是真命题,故A不符合题意;
B、同旁内角互补是假命题,故B符合题意;
C、全等三角形的对应边相等是真命题,故C不符合题意;
D、角平分线上的点到这个角的两边的距离相等.是真命题,故D不符合题意;、
故答案为:B.
【分析】利用对顶角的性质,可对A作出判断;利用两直线平行,同旁内角互补,可对B作出判断;利用全等三角形的性质,可对C作出判断;利用角平分线的性质,可对D作出判断,由此可得到是假命题的选项.
10.【答案】 B
【解析】【解答】解: ∵∠AOC=90° ,
∴∠COE+∠AOE=90° ,
即 ∠AOE 的余角是 ∠COE ;
又 ∵∠EOF=90° , ∠AOB=180° ,
∴∠BOF+∠AOE=90° ,
即 ∠AOE 的余角是 ∠BOF .
故答案为:B
【分析】根据互余的定义,即是求与 ∠AOE 的和是 90° 的角,根据角相互间的和差关系可得.本题主要考查了平角,余角的定义,是一个基本的类型,熟记定义是关键.
二、填空题
11.【答案】 4
【解析】【解答】解:∵DE平分∠ADC,CE平分∠DCB,
∴∠ADE=∠EDC,∠ECD=∠ECB.
∵AD∥BF,
∴∠A+∠ABF=180°,
∴∠ADC+∠DCB+∠CBF=180°,
∴2∠EDC+2∠BCE+54∠BCE=180°.
∵∠DEC=115°,
∴∠EDC+∠ECD=65°,
∴∠EDC+∠BCE=65°,
∴∠BCE=40°,∠EDC=25°,
∴∠CBF=54∠BCE=50°,
∴∠CFB=90°,
∴BF⊥EC,
∴CE=2BF,设BF=m,则CE=2m.
∵S△BCE=?12EC·BF=4,
∴12×2m×m=4,
∴m=2或-2(舍去),
∴CE=2m=4.
故答案为:4.
【分析】由AD∥BF,可得∠A+∠ABF=180°,进而由四边形内角和为360°可得∠ADC+∠DCB+∠BCE=180°,由∠DEC=115°,可得∠EDC+∠DCE=65°,然后结合角平分线的概念可求得∠BCE、∠EDC、∠CBF的度数,然后求出∠CFB=90°,再利用三角形的面积公式求解即可.
12.【答案】 405°
【解析】【解答】解:根据正方形的性质和全等三角形的性质可知,
∠1+∠9=90°,∠2+∠6=90°,∠3=∠5=∠7=45°,∠4+∠8=90°,
∴ ∠1+∠2+∠3+?+∠9=3×90°+3×45°=405°?,
故答案为:405°.
【分析】根据正方形的性质和全等三角形的性质分析,找出互余的三对角,结合等腰直角三角形的性质即可求出这几个角的和.
13.【答案】 21°18′
【解析】【解答】解: ∵ ∠α=68°42'
∴ ∠α 的余角为 90°?68°42′=89°60′?68°42′=21°18′
故答案为:21°18′.
【分析】根据互为余角的两个角的和等于90°,列式计算即可.
14.【答案】 5
【解析】【解答】解:∵EB⊥AC,CD⊥AC,
∴EB∥CD,
∴△AEB∽△ADC,
∴BEAB=CDAC ,
∴1.53=CD10 ,
∴CD=5.
故答案为:5.
【分析】根据垂直于同一直线的两直线互相平行可得EB∥CD,进而推出△AEB∽△ADC,然后借助相似三角形对应边成比例就可求得CD的值.
15.【答案】 55°
【解析】【解答】解:如图,
∵AB⊥BC,∴∠3=90°﹣∠1=55°.
∵a∥b,∴∠2=∠3=55°.
故答案为:55°.
【分析】根据垂直的定义及平角的定义,可求得∠3=55°,根据两直线平行同位角相等可得∠2=∠3=55°.
16.【答案】 132°
【解析】【解答】解:∵AB⊥AE,
∴∠BAC+∠CAE=90°
∴∠BAC=90°-42°=48°,
∵AB∥CD,
∴∠ACD+∠BAC=180°,
∴∠ACD=180°-48°=132°.
故答案为:132°.
【分析】利用垂直的定义可证得∠BAC+∠CAE=90°,由此可求出∠BAC的度数;再利用两直线平行,同旁内角互补,就可求出∠ACD的度数.
17.【答案】 31°34′
【解析】【解答】解:由余角的定义得:∠α=90°﹣58°26′=31°34′,
故答案为:31°34′.
【分析】根据和为90°的两个角就互为余角即可得出答案.
18.【答案】 128.25
【解析】【解答】解: ∵∠α 的余角是 38°15' ,
∴∠a 的补角为: 38°15'+90°=128.25° .
故答案为:128.25.
【分析】根据同角的补角比余角大90°即可求出答案.
19.【答案】 170
【解析】【解答】解: ∵α=50° ,
∴ 根据互为补角的概念,得
α 的补角为: 180°?50°=130° ,
根据互为余角的概念,得,
α 的余角为: 90°?50°=40° ,
∴ 余角与补角的度数和为: 130°+40°=170° .
故答案为170.
【分析】此题考查余角和补角的概念,如果两个角的和等于 180°( 平角 ) ,就说这两个角互为补角.如果两个角和为 90° ,则两个角互为余角.根据概念先求出 α 的余角和补角,再进行相加计算即可.
三、解答题
20.【答案】 解:如图,延长AE交BC于点F,
∵点E是CD的中点 ∴DE=CE,
∵AB⊥BC,AB⊥AD ∴AD∥BC
∴∠ADE=∠BCE且DE=CE,∠AED=∠CEF
∴△AED≌△FEC(ASA)
∴AD=FC=5,AE=EF
∴BF=BC﹣FC=5
∴在Rt△ABF中,AF= AB2+BF2 =13
∴AE= AF2 = 132
【解析】【分析】 延长AE交BC于点F,易证△AED≌△FEC,然后由全等三角形对应边相等可求出AD、FC、BF的值,接下来在Rt△ABF中,根据勾股定理可得AF的值,最后根据AE=EF就可得到AE的值.
21.【答案】 解:∠E=∠F.理由如下:
∵AB∥CD,
∴∠A=∠EDC.
∵∠A=∠C,
∴∠EDC=∠C,
∴AE∥CF,
∴∠E=∠F.
【解析】【分析】由AB∥CD,根据平行线的性质得∠A=∠EDC,而∠A=∠C,则∠EDC=∠C,根据平行线的判定得到AE∥CF,然后再根据平行线的性质得到∠E=∠F.
22.【答案】 解: ∵AB//CD (已知),
∴∠B=∠C (两直线平行,内错角相等)
∵BF=CE (已知),
∴BF+EF=CE+EF ,即 BE=CF .
在 ΔABE 和 ΔDCF 中,
{AB=CD∠B=∠CBE=CF ,
∴ΔABE?ΔDCF(SAS)
【解析】【分析】?根据两直线平行,内错角相等,可得∠B=∠C,由BF=CE得出BE=CF,根据SAS可证△ABE≌△DCF.
23.【答案】 证明:∵AD平分∠BAC,
∴∠DAB=∠DAC
∵∠BFE=∠DAC,
∴∠BFE=∠DAB,
∴AD∥EG,
∴∠G=∠DAC
又∵∠BFE=∠DAC,
∴∠G=∠BFE,
由对顶角相等得:∠BFE=∠AFG,
∴∠G=∠AFG.
【解析】【分析】利用角平分线的定义可得到∠DAB=∠DAC,结合已知可推出∠BFE=∠DAB;再利用两直线平行同位角相等可证得∠G=∠DAC,由此可得到∠G=∠BFE,然后可证得结论.
24.【答案】 解:设这个角是 α ,则它的余角为 90°?α ,补角为 180°?α ,
由题意得, 90°?α=12(180°?α)?18° ,
解得 α=36° ,
90°?36°=54° .
答:这个角是 36° ,它的余角是 54°
【解析】【分析】设这个角是 α ,然后表示出它的余角和补角,再列出方程求解即可.
四、作图题
25.【答案】 解:所以如图为所求做图形.
PE>PD
理由:点到直线垂线段最短.
【解析】【分析】 (1)根据垂线的定义即可过点P画AB的垂线,垂足为点D;
(2)根据平行线的定义即可过点P画BC的平行线交AB于点E;
(3)由垂线段最短可知PE>PD.
26.【答案】 解:直线CD\AE,点F如图所示;
【解析】【分析】(1)根据直线的定义,平行线的定义画出图形即可.(2)根据直线的定义,垂线的定义画出图形即可.
五、综合题
27.【答案】 (1)解: DE 与 BF 的位置关系为: DE//BF ,理由如下:
如图1所示:
∵∠A=∠C=90° , ∴∠ADC+∠ABC=360°?(∠A+∠C)=180° ,
∵DE 、 BF 分别平分 ∠ADC 、 ∠ABC , ∴∠ADE=12∠ADC , ∠ABF=12∠ABC ,
∴∠ADE+∠ABF=12×180°=90° ,
∵∠ADE+∠AED=90° , ∴∠AED=∠ABF , ∴DE//BF ;
(2)解:令 x=0 ,得 y=12 , ∴DE=12 ,
令 y=0 ,得 x=10 , ∴MN=10 ,
把 y=245 代入 y=?65x+12 ,
解得: x=6 ,即 NQ=6 , ∴QM=10?6=4 ,
∵Q 是 BF 中点, ∴FQ=QB ,
∵BM=2FN , ∴FN+6=4+2FN ,
解得: FN=2 , ∴BM=4 , ∴BF=FN+MN+MB=16 ;
(3)解:①连接 EM 并延长交 BC 于点 H ,如图2所示:
∵FM=2+10=12=DE , DE//BF ,四边形 DFME 是平行四边形, ∴DF=EM ,
∵AD=6 , DE=12 , ∠A=90° , ∴∠DEA=30° , ∴∠DEA=∠FBE=∠FBC=30° ,
∴∠ADE=60° , ∴∠ADE=∠CDE=∠FME=60° ,
∴∠DFM=∠DEM=120° , ∴∠MEB=180°?120°?30°=30° ,
∴∠MEB=∠FBE=30° , ∴∠EHB=180°?30°?30°?30°=90° , DF=EM=BM=4 ,
∴MH=12BM=2 , ∴EH=4+2=6 ,
由勾股定理得: HB=BM2?MH2=42?22=23 ,
∴BE=EH2?HB2=62+(23)2=43 ,
当 DP=DF 时, ?65x+12=4 ,解得: x=203 ,
∴BQ=14?x=14?203=223 ,
223>43 , ∴BQ>BE ;
②(Ⅰ)当 PQ 经过点 D 时,如图3所示:
y=0 ,则 x=10 ;
(Ⅱ)当 PQ 经过点 C 时,如图4所示:
∵BF=16 , ∠FCB=90° , ∠CBF=30° , ∴CF=12BF=8 , ∴CD=8+4=12 ,
∵FQ//DP , ∴ΔCFQ∽ΔCDP , FQDP=CFCD , 2+x?65x+12=812 ,解得: x=103 ;
(Ⅲ)当 PQ 经过点 A 时,如图5所示:
∵PE//BQ , ∴ΔAPE∽ΔAQB , PEBQ=AEAB ,
由勾股定理得: AE=DE2?AD2=122?62=63 ,
∴AB=63+43=103 , 12?(?65x+12)14?x=63103 ,
解得: x=143 ,
由图可知, PQ 不可能过点 B ;
综上所述,当 x=10 或 x=103 或 x=143 时, PQ 所在的直线经过四边形 ABCD 的一个顶点.
【解析】【分析】(1)首先由四边形内角和为360°可得∠ADC+∠ABC=180°,然后根据角平分线的定义可得∠ADE+∠ABF的度数,结合∠ADE+∠AED=90°可得∠AED与∠ABF的数量关系,进而判断DE与BF的位置关系;
(2)分别令x=0、y=0求出对应的y、x的值,即为DE、MN的值,把y=245代入求出x的值,即为NQ的值,然后根据QM=MN-NQ求出QM的值,由Q为BF的中点以及BM=2FN可得到关于FN的等式,进而求出FN的值,最后根据BF=FN+MN+MB计算即可;
(3)①连接EM并延长交BC于点H,可推出四边形DFME为平行四边形,由平行四边形的性质以及平行线的性质可求得∠DEA,∠ADE,∠DFM,∠MEB,∠EHB的度数,进一步得到MH、EH的值,然后利用勾股定理求出HB、BE的值,利用DP=DF可得关于x的方程,求解即可;
②当PQ经过点C时,首先求出CF、CD的值,由△CFQ∽△CDP可得关于x的方程,求解即可;当PQ经过点A时,易证△APE∽△AQB,由勾股定理求出AE的值,进而得到AB的值,然后利用相似三角形对应边成比例可得关于x的方程,求解即可.
28.【答案】 (1)解: ∵AE平分∠BAD (已知),
∴∠BAD=2∠1 (角平分线的定义? ),
∵BE平分∠ABC (已知),
∴∠ABC=2∠2 (角平分线的定义? ),
∴∠BAD+∠ABC=2∠1+2∠2 (??? 等量代换????? ),
∵∠1+∠2=90° (已知),
∴∠BAD+∠ABC=180°
∴AD//BC (? 同旁内角互补,两直线平行? ).
(2)解: ∵∠1+∠2+∠AEB=180°,∠1+∠2=90°
∴∠AEB=90°=∠AEF+∠BEF
∵∠AED+∠AEB+∠CEB=180°
∴∠AED+∠CEB=90°
∵AE 平分 ∠DEF
∴∠AED=∠AEF
∴∠BEF=∠CEB (等角的余角相等)
∴BE 平分 ∠CEF
【解析】【分析】(1)首先根据角平分线定义可得∠BAD=2∠1,∠ABC=2∠2,则由等量代换可得∠BAD+∠ABC=2∠1+2∠2,根据同旁内角互补,两直线平行可得AD∥BC;
(2)由三角形内角和定理,结合∠1和∠2互余可得∠AEB为90°,从而得出∠AED和∠BEC互余,则由AE平分∠DEF,根据余角的性质得出BE平分∠CEF.
29.【答案】 (1)解:设 ∠BOC=x ,则 ∠AOC=2x ,
依题意列方程 90°?2x=x?30° ,
解得: x=40° ,
即 ∠AOB=40°
(2)解:由 (1) 得, ∠AOC=80° ,
①当射线OD在 ∠AOC 内部时, ∠AOD=20° ,
则 ∠COD=∠AOC?∠AOD=60° ;
②当射线OD在 ∠AOC 外部时, ∠AOD=20° ,
则 ∠COD=∠AOC+∠AOD=100° .
【解析】【分析】(1)设 ∠BOC=x ,则 ∠AOC=2x ,根据∠AOC 的余角比 ∠BOC 小 30゜ 列方程求解即可;
(2)分两种情况:①当射线OD在 ∠AOC内部,②当射线OD在 ∠AOC 外部,分别求出 ∠COD 的度数即可.
30.【答案】 (1)解: ∵∠COF 与 ∠DOF 是邻补角,
∴∠COF=180°?∠DOF=90° .
∵∠AOC 与 ∠AOF 互为余角,
∴∠AOC=90°?∠AOF=90°?50°=40° .
∵∠AOC 与 ∠BOC 是邻补角,
∴∠COB=180°?∠AOC=180°?40°=140° .
∵OE 平分 ∠BOC ,
∴∠BOE=12∠BOC=70°
(2)解: ∠BOD : ∠BOE=1 :4,
设 ∠BOD=∠AOC=x , ∠BOE=∠COE=4x .
∵∠AOC 与 ∠BOC 是邻补角,
∴∠AOC+∠BOC=180° ,
即 x+4x+4x=180° ,
解得 x=20° .
∵∠AOC 与 ∠AOF 互为余角,
∴∠AOF=90°?∠AOC=90°?20°=70°
【解析】【分析】(1)根据补角,余角的关系,可得 ∠COB ,根据角平分线的定义,可得答案;
(2)根据邻补角,可得关于x的方程,解方程可得 ∠AOC ,再根据余角的定义,可得答案.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
