人教版数学 七年级下册 5.1.1 相交线 同步练习(Word版 含答案)
文档属性
| 名称 | 人教版数学 七年级下册 5.1.1 相交线 同步练习(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 83.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-29 00:00:00 | ||
图片预览



文档简介
5.1.1 相交线
1.如图,点O在直线AB上.若∠BOC=60°,则∠AOC的大小是( )
A.60° B.90° C.120° D.150°
2.如图,直线AB和CD相交于点O,则∠AOC的邻补角是 .
3.如图,直线AB和CD相交于点O,OE平分∠BOD.若∠BOE=30°,则∠AOD= .
4.下列图形中,∠1与∠2是对顶角的是( )
5.(2020·安顺)如图,直线a,b相交于点O,如果∠1+∠2=60°,那么∠3是( )
A.150° B.120° C.60° D.30°
6.如图是对顶角量角器,用它测量角的原理是 .
7.在括号内填写依据:
如图,因为直线a,b相交于点O,
所以∠1+∠3=180°( ),
∠1=∠2( ).
8.如图,直线AB,CD相交于点O,∠AOC=60°,∠1=40°,则∠2= ,∠AOE= .
9.如图,直线AB,CD相交于点O,∠EOC=70°,OA平分∠EOC,求∠BOD的度数.
10.下列说法正确的有( )
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个 B.2个 C.3个 D.4个
11.两条直线相交所成的四个角中,有两个角分别是(2x-10)°和(110-x)°,则x= .
12.如图,三条直线l1,l2,l3相交于一点,则∠1+∠2+∠3等于( )
A.90° B.120° C.180° D.360°
13.如图,直线AB,CD相交于点O,OE平分∠BOD.若∠AOD=110°,则∠COE的度数为( )
A.135° B.145° C.155° D.125°
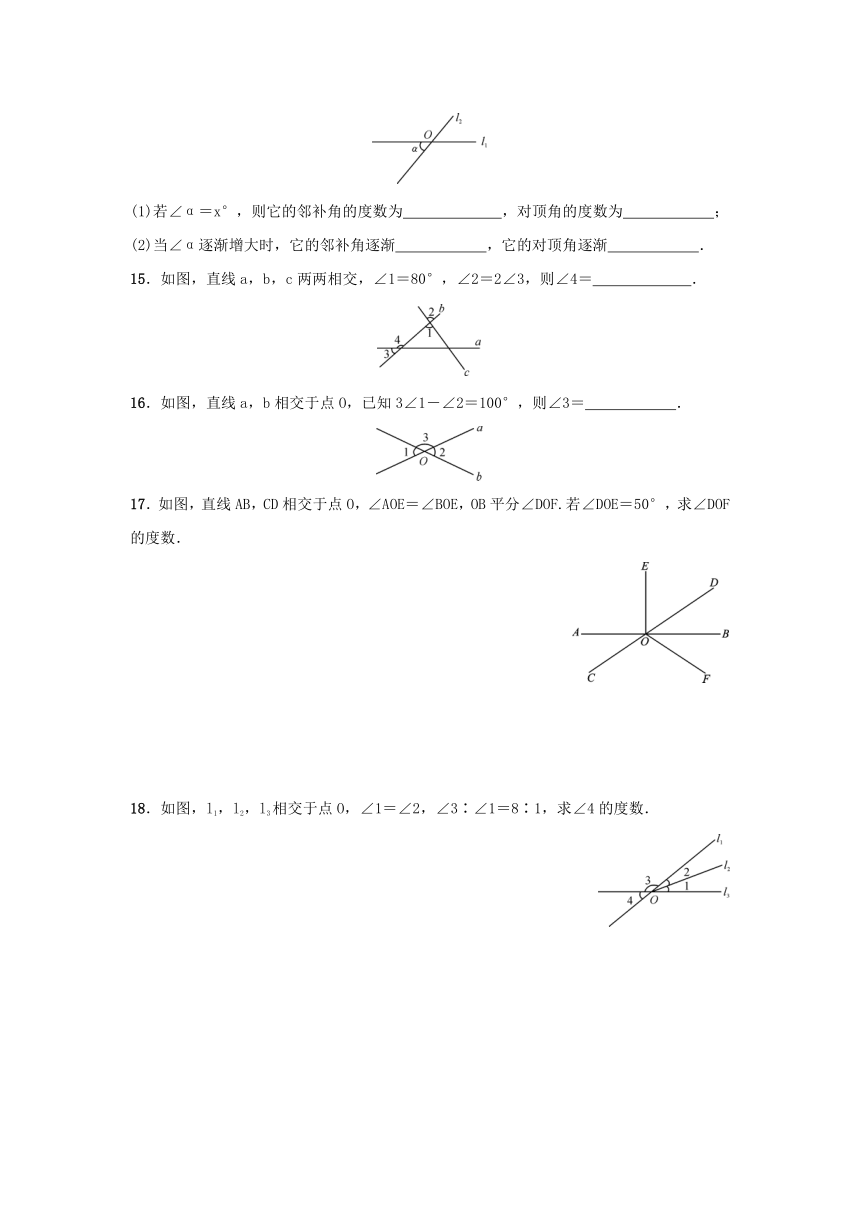
14.如图,两条直线l1,l2相交于点O.
(1)若∠α=x°,则它的邻补角的度数为 ,对顶角的度数为 ;
(2)当∠α逐渐增大时,它的邻补角逐渐 ,它的对顶角逐渐 .
15.如图,直线a,b,c两两相交,∠1=80°,∠2=2∠3,则∠4= .
16.如图,直线a,b相交于点O,已知3∠1-∠2=100°,则∠3= .
17.如图,直线AB,CD相交于点O,∠AOE=∠BOE,OB平分∠DOF.若∠DOE=50°,求∠DOF的度数.
18.如图,l1,l2,l3相交于点O,∠1=∠2,∠3∶∠1=8∶1,求∠4的度数.
19.探究题:
(1)三条直线相交,最少有 个交点,最多有 个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有 个交点,最多有 个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有1个交点,最多有 个交点,对顶角有 对,邻补角有 对.
参考答案:
1.如图,点O在直线AB上.若∠BOC=60°,则∠AOC的大小是( C )
A.60° B.90° C.120° D.150°
2.如图,直线AB和CD相交于点O,则∠AOC的邻补角是∠AOD和∠BOC.
3.如图,直线AB和CD相交于点O,OE平分∠BOD.若∠BOE=30°,则∠AOD=120°.
4.下列图形中,∠1与∠2是对顶角的是( C )
5.(2020·安顺)如图,直线a,b相交于点O,如果∠1+∠2=60°,那么∠3是( A )
A.150° B.120° C.60° D.30°
6.如图是对顶角量角器,用它测量角的原理是对顶角相等.
7.在括号内填写依据:
如图,因为直线a,b相交于点O,
所以∠1+∠3=180°(邻补角互补),
∠1=∠2(对顶角相等).
8.如图,直线AB,CD相交于点O,∠AOC=60°,∠1=40°,则∠2=20°,∠AOE=140°.
9.如图,直线AB,CD相交于点O,∠EOC=70°,OA平分∠EOC,求∠BOD的度数.
解:因为OA平分∠EOC,∠EOC=70°,
所以∠AOC=∠EOC=35°,
所以∠BOD=∠AOC=35°.
10.下列说法正确的有(B)
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个 B.2个 C.3个 D.4个
11.两条直线相交所成的四个角中,有两个角分别是(2x-10)°和(110-x)°,则x=40或80.
12.如图,三条直线l1,l2,l3相交于一点,则∠1+∠2+∠3等于( C )
A.90° B.120° C.180° D.360°
13.如图,直线AB,CD相交于点O,OE平分∠BOD.若∠AOD=110°,则∠COE的度数为(B)
A.135° B.145° C.155° D.125°
14.如图,两条直线l1,l2相交于点O.
(1)若∠α=x°,则它的邻补角的度数为(180-x)°,对顶角的度数为x°;
(2)当∠α逐渐增大时,它的邻补角逐渐减小,它的对顶角逐渐增大.
15.如图,直线a,b,c两两相交,∠1=80°,∠2=2∠3,则∠4=140°.
16.如图,直线a,b相交于点O,已知3∠1-∠2=100°,则∠3=130°.
17.如图,直线AB,CD相交于点O,∠AOE=∠BOE,OB平分∠DOF.若∠DOE=50°,求∠DOF的度数.
解:因为∠AOE=∠BOE,且∠AOE+∠BOE=180°,
所以∠AOE=∠BOE=90°.
因为∠DOE=50°,
所以∠DOB=∠BOE-∠DOE=40°.
因为OB平分∠DOF,
所以∠DOF=2∠DOB=80°.
18.如图,l1,l2,l3相交于点O,∠1=∠2,∠3∶∠1=8∶1,求∠4的度数.
解:设∠1=∠2=x°,则∠3=8x°.
由∠1+∠2+∠3=180°,得
10x=180.解得x=18.
所以∠1=∠2=18°.
所以∠4=∠1+∠2=36°.
19.探究题:
(1)三条直线相交,最少有1个交点,最多有3个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有1个交点,最多有6个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有1个交点,最多有个交点,对顶角有n(n-1)对,邻补角有2n(n-1)对.
解:(1)图略,对顶角有6对,邻补角有12对.
(2)图略,对顶角有12对,邻补角有24对.
1.如图,点O在直线AB上.若∠BOC=60°,则∠AOC的大小是( )
A.60° B.90° C.120° D.150°
2.如图,直线AB和CD相交于点O,则∠AOC的邻补角是 .
3.如图,直线AB和CD相交于点O,OE平分∠BOD.若∠BOE=30°,则∠AOD= .
4.下列图形中,∠1与∠2是对顶角的是( )
5.(2020·安顺)如图,直线a,b相交于点O,如果∠1+∠2=60°,那么∠3是( )
A.150° B.120° C.60° D.30°
6.如图是对顶角量角器,用它测量角的原理是 .
7.在括号内填写依据:
如图,因为直线a,b相交于点O,
所以∠1+∠3=180°( ),
∠1=∠2( ).
8.如图,直线AB,CD相交于点O,∠AOC=60°,∠1=40°,则∠2= ,∠AOE= .
9.如图,直线AB,CD相交于点O,∠EOC=70°,OA平分∠EOC,求∠BOD的度数.
10.下列说法正确的有( )
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个 B.2个 C.3个 D.4个
11.两条直线相交所成的四个角中,有两个角分别是(2x-10)°和(110-x)°,则x= .
12.如图,三条直线l1,l2,l3相交于一点,则∠1+∠2+∠3等于( )
A.90° B.120° C.180° D.360°
13.如图,直线AB,CD相交于点O,OE平分∠BOD.若∠AOD=110°,则∠COE的度数为( )
A.135° B.145° C.155° D.125°
14.如图,两条直线l1,l2相交于点O.
(1)若∠α=x°,则它的邻补角的度数为 ,对顶角的度数为 ;
(2)当∠α逐渐增大时,它的邻补角逐渐 ,它的对顶角逐渐 .
15.如图,直线a,b,c两两相交,∠1=80°,∠2=2∠3,则∠4= .
16.如图,直线a,b相交于点O,已知3∠1-∠2=100°,则∠3= .
17.如图,直线AB,CD相交于点O,∠AOE=∠BOE,OB平分∠DOF.若∠DOE=50°,求∠DOF的度数.
18.如图,l1,l2,l3相交于点O,∠1=∠2,∠3∶∠1=8∶1,求∠4的度数.
19.探究题:
(1)三条直线相交,最少有 个交点,最多有 个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有 个交点,最多有 个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有1个交点,最多有 个交点,对顶角有 对,邻补角有 对.
参考答案:
1.如图,点O在直线AB上.若∠BOC=60°,则∠AOC的大小是( C )
A.60° B.90° C.120° D.150°
2.如图,直线AB和CD相交于点O,则∠AOC的邻补角是∠AOD和∠BOC.
3.如图,直线AB和CD相交于点O,OE平分∠BOD.若∠BOE=30°,则∠AOD=120°.
4.下列图形中,∠1与∠2是对顶角的是( C )
5.(2020·安顺)如图,直线a,b相交于点O,如果∠1+∠2=60°,那么∠3是( A )
A.150° B.120° C.60° D.30°
6.如图是对顶角量角器,用它测量角的原理是对顶角相等.
7.在括号内填写依据:
如图,因为直线a,b相交于点O,
所以∠1+∠3=180°(邻补角互补),
∠1=∠2(对顶角相等).
8.如图,直线AB,CD相交于点O,∠AOC=60°,∠1=40°,则∠2=20°,∠AOE=140°.
9.如图,直线AB,CD相交于点O,∠EOC=70°,OA平分∠EOC,求∠BOD的度数.
解:因为OA平分∠EOC,∠EOC=70°,
所以∠AOC=∠EOC=35°,
所以∠BOD=∠AOC=35°.
10.下列说法正确的有(B)
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个 B.2个 C.3个 D.4个
11.两条直线相交所成的四个角中,有两个角分别是(2x-10)°和(110-x)°,则x=40或80.
12.如图,三条直线l1,l2,l3相交于一点,则∠1+∠2+∠3等于( C )
A.90° B.120° C.180° D.360°
13.如图,直线AB,CD相交于点O,OE平分∠BOD.若∠AOD=110°,则∠COE的度数为(B)
A.135° B.145° C.155° D.125°
14.如图,两条直线l1,l2相交于点O.
(1)若∠α=x°,则它的邻补角的度数为(180-x)°,对顶角的度数为x°;
(2)当∠α逐渐增大时,它的邻补角逐渐减小,它的对顶角逐渐增大.
15.如图,直线a,b,c两两相交,∠1=80°,∠2=2∠3,则∠4=140°.
16.如图,直线a,b相交于点O,已知3∠1-∠2=100°,则∠3=130°.
17.如图,直线AB,CD相交于点O,∠AOE=∠BOE,OB平分∠DOF.若∠DOE=50°,求∠DOF的度数.
解:因为∠AOE=∠BOE,且∠AOE+∠BOE=180°,
所以∠AOE=∠BOE=90°.
因为∠DOE=50°,
所以∠DOB=∠BOE-∠DOE=40°.
因为OB平分∠DOF,
所以∠DOF=2∠DOB=80°.
18.如图,l1,l2,l3相交于点O,∠1=∠2,∠3∶∠1=8∶1,求∠4的度数.
解:设∠1=∠2=x°,则∠3=8x°.
由∠1+∠2+∠3=180°,得
10x=180.解得x=18.
所以∠1=∠2=18°.
所以∠4=∠1+∠2=36°.
19.探究题:
(1)三条直线相交,最少有1个交点,最多有3个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有1个交点,最多有6个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有1个交点,最多有个交点,对顶角有n(n-1)对,邻补角有2n(n-1)对.
解:(1)图略,对顶角有6对,邻补角有12对.
(2)图略,对顶角有12对,邻补角有24对.
