11.1.3多面体与棱柱 34张课件 2020-2021学年高一下学期数学人教B版(2019)必修第四册
文档属性
| 名称 | 11.1.3多面体与棱柱 34张课件 2020-2021学年高一下学期数学人教B版(2019)必修第四册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 617.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 09:52:54 | ||
图片预览








文档简介
11.1.3 多面体与棱柱
新课程标准
素养风向标
1.了解多面体的概念及特征.
2.理解棱柱概念及结构特征.
1.了解多面体的定义及其分类.(数学抽象)
2.理解棱柱的定义和结构特征.(直观想
象)
基础预习初探
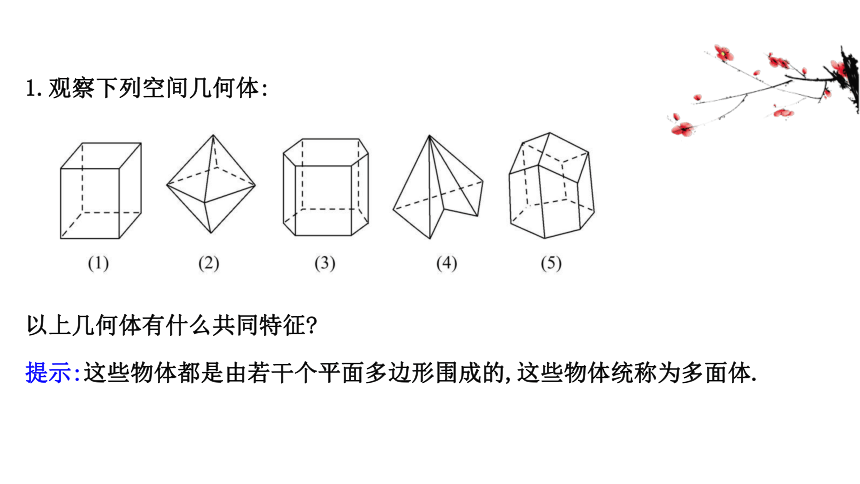
1.观察下列空间几何体:
以上几何体有什么共同特征?
提示:这些物体都是由若干个平面多边形围成的,这些物体统称为多面体.
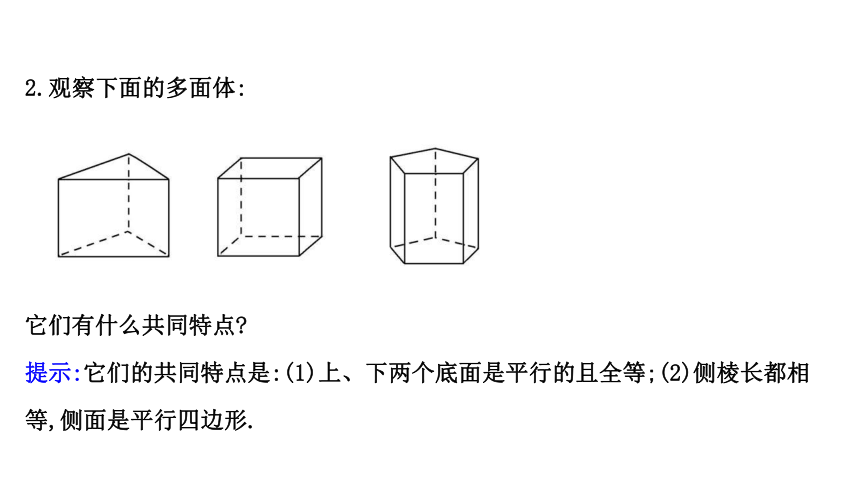
2.观察下面的多面体:
它们有什么共同特点?
提示:它们的共同特点是:(1)上、下两个底面是平行的且全等;(2)侧棱长都相等,侧面是平行四边形.
【概念生成】
1.多面体的有关概念:
(1)定义:
一般地,由若干个___________所围成的封闭几何体称为多面体.
(2)各部分名称:
①面:围成多面体的各个多边形;
②棱:相邻两个面的_______;
③顶点:棱与棱的公共点.
平面多边形
公共边
④面对角线:一个多面体中连接_________________的线段,如果不是多面体的
棱,就称其为多面体的面对角线.
⑤体对角线:连接_______________________的线段称为多面体的体对角线.
⑥截面:一个几何体和一平面相交所得的_________(包含它的内部),称为这个
几何体的一个截面.
同一面上两个顶点
不在同一面上的两个顶点
平面图形
2.棱柱
(1)定义:有两个面互相平行,且该多面体的顶点都在这两个面上,其余各面都是平行四边形,这样的多面体称为棱柱.
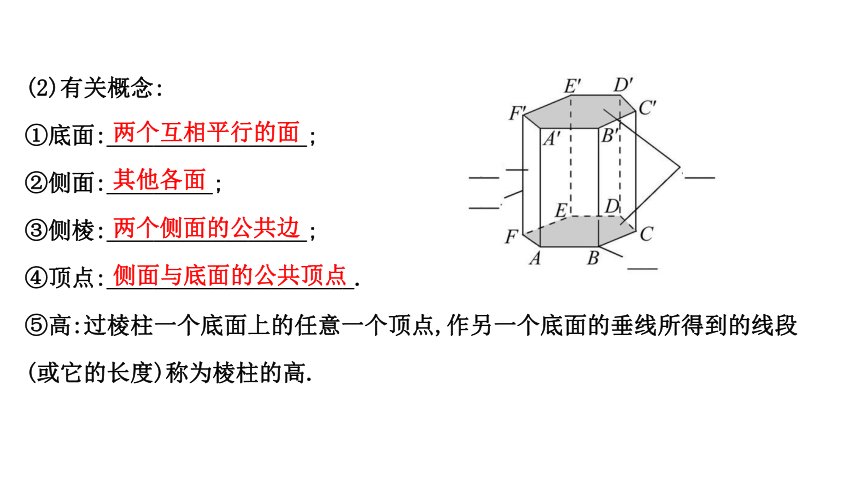
(2)有关概念:
①底面:_________________;
②侧面:_________;
③侧棱:_________________;
④顶点:_____________________.
⑤高:过棱柱一个底面上的任意一个顶点,作另一个底面的垂线所得到的线段
(或它的长度)称为棱柱的高.
两个互相平行的面
其他各面
两个侧面的公共边
侧面与底面的公共顶点
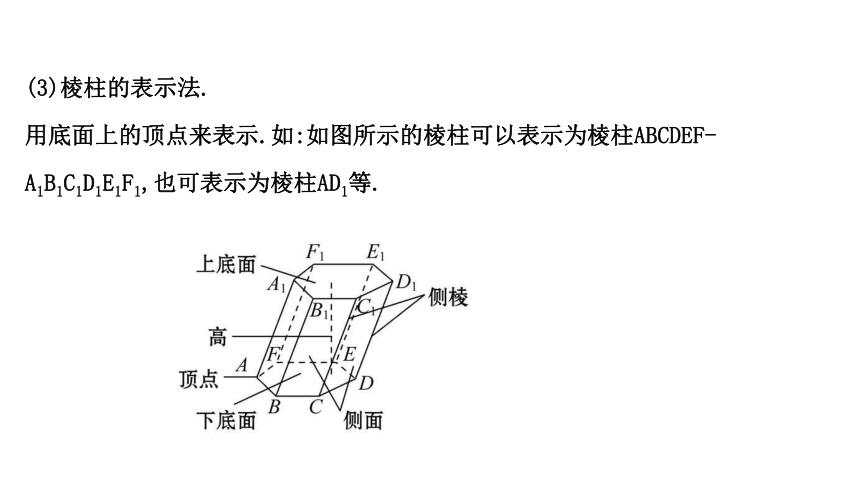
(3)棱柱的表示法.
用底面上的顶点来表示.如:如图所示的棱柱可以表示为棱柱ABCDEF-A1B1C1D1E1F1,也可表示为棱柱AD1等.
(4)棱柱的分类.
按底面的_____分为:三棱柱、四棱柱、五棱柱……
棱柱又分为斜棱柱和直棱柱.
①斜棱柱:侧棱_______于底面的棱柱.
②直棱柱:侧棱_____于底面的棱柱.
③正棱柱:底面是正多边形的_______.
形状
不垂直
垂直
直棱柱
④平行六面体:底面是___________的棱柱,即平行六面体的六个面都是平行四
边形.
⑤长方体:底面是矩形的_____________.
⑥正方体:棱长都相等的_______.
平行四边形
直平行六面体
长方体
核心互动探究
探究点一 对多面体的识别和判断
【典例1】如图,长方体ABCD-A1B1C1D1.
(1)这个长方体是棱柱吗?如果是,是几棱柱?为什么?
(2)用平面BCNM把这个长方体分成两部分,各部分形成的
几何体还是棱柱吗?如果是,是几棱柱,并用符号表示.
【思维导引】观察图形→紧扣概念→得出结论→回答问题
【解析】(1)长方体ABCD-A1B1C1D1是棱柱,且是四棱柱.
因为平面ABCD与平面A1B1C1D1平行,且其余各面都是平行四边形,且顶点都在这两个面上.
(2)用平面BCNM把这个长方体分成两部分,其中一部分有两个平行的平面BB1M与平面CC1N,其余各面都是四边形,并且顶点都在这两个面上,符合棱柱的定义,所以是三棱柱,可用符号表示为三棱柱BB1M-CC1N;另一部分有两个平行的平面ABMA1与平面DCND1,其余各面都是四边形,并且顶点都在这两个面上,符合棱柱的定义,所以是四棱柱,可用符号表示为四棱柱ABMA1-DCND1.
【类题通法】
正确判断几何体类型的方法
要正确判断几何体的类型,就要熟练掌握各类简单几何体的结构特征.对于有些四棱柱,互相平行的平面不只是两个,所以对于底面来说并不固定.棱柱的概念中两个面互相平行,指的是两个底面互相平行.但由于棱柱的放置方式不同,两个底面的位置就不一样,但无论如何放置,都应该满足棱柱的定义.
提醒:判断棱柱的关键是看该几何体是否满足棱柱的概念,特别是看其是否存在两个互相平行的面.
【定向训练】
下列图形经过折叠可以围成一个棱柱的是 ( )
【解析】选D.A,B,C中底面图形的边数与侧面的个数不一致,故不能围成棱柱.
【补偿训练】
有两个面互相平行,其余各面均为平行四边形的几何体一定是棱柱.这种说法是否正确?如果正确,说明理由;若不正确,举出反例.
【解析】这种说法不正确.如图所示的几何体,它由两个等底的四棱柱组合而成,它有两个面相互平行,其余各面都是平行四边形,但相邻的两个侧面的公共边并不都平行.因此该几何体不是棱柱.
探究点二 几种常见四棱柱的关系
【典例2】下列说法正确的是 ( )
A.棱柱的面中,至少有两个互相平行
B.棱柱中两个互相平行的平面一定是棱柱的底面
C.棱柱中各条棱长都相等
D.棱柱的侧面是平行四边形,但它的底面一定不是平行四边形
【思维导引】依据棱柱的相关概念判断.
【解析】选A.由棱柱的定义知,棱柱的底面平行,故A正确;正方体相对的两个面平行,但其也可以是侧面,故B错误;棱柱的侧棱相等,但是各条棱不一定都相等,故C错误;棱柱的侧面一定是平行四边形,但它的底面可以是平行四边形,也可以是其他多边形,故D错误.
【类题通法】
几种常见四棱柱的关系
【定向训练】
一个棱柱是正四棱柱的条件是 ( )
A.底面是正方形,有两个面是矩形的四棱柱
B.底面是正方形,两个侧面垂直于底面的四棱柱
C.底面是菱形,且有个顶点处的两条棱互相垂直的四棱柱
D.底面是正方形,每个侧面都是全等的矩形的四棱柱
【解析】选D.选项A,B中,两个面为相对侧面时,四棱柱不一定是直四棱柱,C中底面不是正方形,故排除选项A,B,C.
探究点三 棱柱中的有关计算
【典例3】在正三棱柱ABC-A1B1C1中,AB=3,AA1=4.M为AA1的中点,P是BC上一点,
且由P沿棱柱侧面经过棱CC1到M的最短路线长为 ,设这条最短路线与CC1的
交点为N.求点P的位置.
【思维导引】把三棱柱的侧面展开后放在平面上,通过列方程来求出点P到点C
的距离,即确定了点P的位置.
【解析】把该三棱柱的侧面展开后如图所示.
设CP=x,则AP=3+x.
根据已知可得方程22+(3+x)2=29.解得x=2(负值舍去).
则点P为BC的三等分点,且靠近点B.
【类题通法】
立体图形的展开问题
解决空间几何体表面上两点间的最短路线问题,一般都是将空间几何体表面展开,转化为求平面内两点间的线段长,这体现了数学中的转化思想.
【定向训练】
如图,在直三棱柱ABB1-DCC1中,∠ABB1=90°,AB=4,BC=2,CC1=1,DC上有一动点P,则△APC1周长的最小值是________.?
【解析】把△DCC1展到四边形ABCD所在的平面上,如图所示,
连接AC1,则PA+PC1≥AC1= =5,
又在直三棱柱ABB1-DCC1中,
AC1=
所以△APC1的周长的最小值为5+ .
答案:5+
【补偿训练】
现有一个底面是菱形的直四棱柱,它的体对角线长为9和15,高是5,求该直四棱柱的侧面积.
【解析】如图,设底面对角线AC=a,BD=b,
交点为O,对角线A1C=15,B1D=9,
所以a2+52=152,b2+52=92,所以a2=200,b2=56.
因为该直四棱柱的底面是菱形,
所以AB2= =64.
所以AB=8.所以直四棱柱的侧面积为4×8×5=160.
【课堂小结】
课堂素养达标
1.在棱柱中,下列说法正确的是 ( )
A.只有两个面平行
B.所有的棱都相等
C.所有的面都是平行四边形
D.两底面平行,且各侧棱也平行
【解析】选D.长方体也是棱柱,以长方体为例,可知A,B不正确,棱柱的两底面可以是三角形,五边形等,故C不正确.
2.下列三种说法中,正确的个数为 ( )
①侧棱垂直于底面的棱柱是直棱柱;
②底面是正多边形的棱柱是正棱柱;
③棱柱的侧面都是平行四边形.
A.0 B.1 C.2 D.3
【解析】选C.由直棱柱的定义,知①正确;由正棱柱的定义,知底面是正多边形的直棱柱是正棱柱,故②错误;由棱柱的定义知其侧面都是平行四边形,故③正确.
3.六面体的体对角线的条数为________.?
【解析】以正方体ABCD-A1B1C1D1为例,如图,其中体对角线为A1C,D1B,AC1,B1D,共4条.
答案:4
4.一个棱柱至少有________个面;面数最少的棱柱有________个顶点,有________条棱.?
【解析】面数最少的棱柱是三棱柱,有5个面,6个顶点,9条棱.
答案:5 6 9
新课程标准
素养风向标
1.了解多面体的概念及特征.
2.理解棱柱概念及结构特征.
1.了解多面体的定义及其分类.(数学抽象)
2.理解棱柱的定义和结构特征.(直观想
象)
基础预习初探
1.观察下列空间几何体:
以上几何体有什么共同特征?
提示:这些物体都是由若干个平面多边形围成的,这些物体统称为多面体.
2.观察下面的多面体:
它们有什么共同特点?
提示:它们的共同特点是:(1)上、下两个底面是平行的且全等;(2)侧棱长都相等,侧面是平行四边形.
【概念生成】
1.多面体的有关概念:
(1)定义:
一般地,由若干个___________所围成的封闭几何体称为多面体.
(2)各部分名称:
①面:围成多面体的各个多边形;
②棱:相邻两个面的_______;
③顶点:棱与棱的公共点.
平面多边形
公共边
④面对角线:一个多面体中连接_________________的线段,如果不是多面体的
棱,就称其为多面体的面对角线.
⑤体对角线:连接_______________________的线段称为多面体的体对角线.
⑥截面:一个几何体和一平面相交所得的_________(包含它的内部),称为这个
几何体的一个截面.
同一面上两个顶点
不在同一面上的两个顶点
平面图形
2.棱柱
(1)定义:有两个面互相平行,且该多面体的顶点都在这两个面上,其余各面都是平行四边形,这样的多面体称为棱柱.
(2)有关概念:
①底面:_________________;
②侧面:_________;
③侧棱:_________________;
④顶点:_____________________.
⑤高:过棱柱一个底面上的任意一个顶点,作另一个底面的垂线所得到的线段
(或它的长度)称为棱柱的高.
两个互相平行的面
其他各面
两个侧面的公共边
侧面与底面的公共顶点
(3)棱柱的表示法.
用底面上的顶点来表示.如:如图所示的棱柱可以表示为棱柱ABCDEF-A1B1C1D1E1F1,也可表示为棱柱AD1等.
(4)棱柱的分类.
按底面的_____分为:三棱柱、四棱柱、五棱柱……
棱柱又分为斜棱柱和直棱柱.
①斜棱柱:侧棱_______于底面的棱柱.
②直棱柱:侧棱_____于底面的棱柱.
③正棱柱:底面是正多边形的_______.
形状
不垂直
垂直
直棱柱
④平行六面体:底面是___________的棱柱,即平行六面体的六个面都是平行四
边形.
⑤长方体:底面是矩形的_____________.
⑥正方体:棱长都相等的_______.
平行四边形
直平行六面体
长方体
核心互动探究
探究点一 对多面体的识别和判断
【典例1】如图,长方体ABCD-A1B1C1D1.
(1)这个长方体是棱柱吗?如果是,是几棱柱?为什么?
(2)用平面BCNM把这个长方体分成两部分,各部分形成的
几何体还是棱柱吗?如果是,是几棱柱,并用符号表示.
【思维导引】观察图形→紧扣概念→得出结论→回答问题
【解析】(1)长方体ABCD-A1B1C1D1是棱柱,且是四棱柱.
因为平面ABCD与平面A1B1C1D1平行,且其余各面都是平行四边形,且顶点都在这两个面上.
(2)用平面BCNM把这个长方体分成两部分,其中一部分有两个平行的平面BB1M与平面CC1N,其余各面都是四边形,并且顶点都在这两个面上,符合棱柱的定义,所以是三棱柱,可用符号表示为三棱柱BB1M-CC1N;另一部分有两个平行的平面ABMA1与平面DCND1,其余各面都是四边形,并且顶点都在这两个面上,符合棱柱的定义,所以是四棱柱,可用符号表示为四棱柱ABMA1-DCND1.
【类题通法】
正确判断几何体类型的方法
要正确判断几何体的类型,就要熟练掌握各类简单几何体的结构特征.对于有些四棱柱,互相平行的平面不只是两个,所以对于底面来说并不固定.棱柱的概念中两个面互相平行,指的是两个底面互相平行.但由于棱柱的放置方式不同,两个底面的位置就不一样,但无论如何放置,都应该满足棱柱的定义.
提醒:判断棱柱的关键是看该几何体是否满足棱柱的概念,特别是看其是否存在两个互相平行的面.
【定向训练】
下列图形经过折叠可以围成一个棱柱的是 ( )
【解析】选D.A,B,C中底面图形的边数与侧面的个数不一致,故不能围成棱柱.
【补偿训练】
有两个面互相平行,其余各面均为平行四边形的几何体一定是棱柱.这种说法是否正确?如果正确,说明理由;若不正确,举出反例.
【解析】这种说法不正确.如图所示的几何体,它由两个等底的四棱柱组合而成,它有两个面相互平行,其余各面都是平行四边形,但相邻的两个侧面的公共边并不都平行.因此该几何体不是棱柱.
探究点二 几种常见四棱柱的关系
【典例2】下列说法正确的是 ( )
A.棱柱的面中,至少有两个互相平行
B.棱柱中两个互相平行的平面一定是棱柱的底面
C.棱柱中各条棱长都相等
D.棱柱的侧面是平行四边形,但它的底面一定不是平行四边形
【思维导引】依据棱柱的相关概念判断.
【解析】选A.由棱柱的定义知,棱柱的底面平行,故A正确;正方体相对的两个面平行,但其也可以是侧面,故B错误;棱柱的侧棱相等,但是各条棱不一定都相等,故C错误;棱柱的侧面一定是平行四边形,但它的底面可以是平行四边形,也可以是其他多边形,故D错误.
【类题通法】
几种常见四棱柱的关系
【定向训练】
一个棱柱是正四棱柱的条件是 ( )
A.底面是正方形,有两个面是矩形的四棱柱
B.底面是正方形,两个侧面垂直于底面的四棱柱
C.底面是菱形,且有个顶点处的两条棱互相垂直的四棱柱
D.底面是正方形,每个侧面都是全等的矩形的四棱柱
【解析】选D.选项A,B中,两个面为相对侧面时,四棱柱不一定是直四棱柱,C中底面不是正方形,故排除选项A,B,C.
探究点三 棱柱中的有关计算
【典例3】在正三棱柱ABC-A1B1C1中,AB=3,AA1=4.M为AA1的中点,P是BC上一点,
且由P沿棱柱侧面经过棱CC1到M的最短路线长为 ,设这条最短路线与CC1的
交点为N.求点P的位置.
【思维导引】把三棱柱的侧面展开后放在平面上,通过列方程来求出点P到点C
的距离,即确定了点P的位置.
【解析】把该三棱柱的侧面展开后如图所示.
设CP=x,则AP=3+x.
根据已知可得方程22+(3+x)2=29.解得x=2(负值舍去).
则点P为BC的三等分点,且靠近点B.
【类题通法】
立体图形的展开问题
解决空间几何体表面上两点间的最短路线问题,一般都是将空间几何体表面展开,转化为求平面内两点间的线段长,这体现了数学中的转化思想.
【定向训练】
如图,在直三棱柱ABB1-DCC1中,∠ABB1=90°,AB=4,BC=2,CC1=1,DC上有一动点P,则△APC1周长的最小值是________.?
【解析】把△DCC1展到四边形ABCD所在的平面上,如图所示,
连接AC1,则PA+PC1≥AC1= =5,
又在直三棱柱ABB1-DCC1中,
AC1=
所以△APC1的周长的最小值为5+ .
答案:5+
【补偿训练】
现有一个底面是菱形的直四棱柱,它的体对角线长为9和15,高是5,求该直四棱柱的侧面积.
【解析】如图,设底面对角线AC=a,BD=b,
交点为O,对角线A1C=15,B1D=9,
所以a2+52=152,b2+52=92,所以a2=200,b2=56.
因为该直四棱柱的底面是菱形,
所以AB2= =64.
所以AB=8.所以直四棱柱的侧面积为4×8×5=160.
【课堂小结】
课堂素养达标
1.在棱柱中,下列说法正确的是 ( )
A.只有两个面平行
B.所有的棱都相等
C.所有的面都是平行四边形
D.两底面平行,且各侧棱也平行
【解析】选D.长方体也是棱柱,以长方体为例,可知A,B不正确,棱柱的两底面可以是三角形,五边形等,故C不正确.
2.下列三种说法中,正确的个数为 ( )
①侧棱垂直于底面的棱柱是直棱柱;
②底面是正多边形的棱柱是正棱柱;
③棱柱的侧面都是平行四边形.
A.0 B.1 C.2 D.3
【解析】选C.由直棱柱的定义,知①正确;由正棱柱的定义,知底面是正多边形的直棱柱是正棱柱,故②错误;由棱柱的定义知其侧面都是平行四边形,故③正确.
3.六面体的体对角线的条数为________.?
【解析】以正方体ABCD-A1B1C1D1为例,如图,其中体对角线为A1C,D1B,AC1,B1D,共4条.
答案:4
4.一个棱柱至少有________个面;面数最少的棱柱有________个顶点,有________条棱.?
【解析】面数最少的棱柱是三棱柱,有5个面,6个顶点,9条棱.
答案:5 6 9
