11.1.5旋转体 39张课件 2020-2021学年高一下学期数学人教B版(2019)必修第四册
文档属性
| 名称 | 11.1.5旋转体 39张课件 2020-2021学年高一下学期数学人教B版(2019)必修第四册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 641.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 09:56:14 | ||
图片预览







文档简介
(共39张PPT)
11.1.5 旋 转 体
新课程标准
素养风向标
1.理解圆柱、圆锥、圆台以及球的概念. .
2.概括并掌握圆柱、圆锥、圆台以及球的结构特征.
1.了解圆柱、圆锥、圆台、球的定义. (数学抽象)
2.掌握圆柱、圆锥、圆台、球的结构特征. (逻辑推理)
3.能够根据圆柱、圆锥、圆台、球的结构特征识别和区分儿何体. (直观想象)
基础预习初探
观察下列实物图,你能说明由该实物图抽象出的几何体与多面体有何不同吗
提示:多面体有棱有侧面,抽象出的几何体没有棱,侧面是一个曲面.
继续探究:
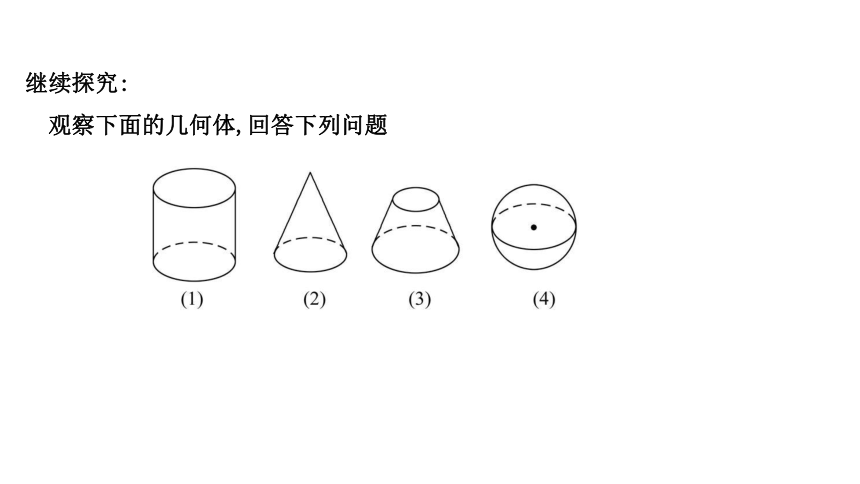
观察下面的几何体,回答下列问题
(1)它们有什么共同点
提示:它们都可以看成是由一个平面图形旋转而生成的.
(2)它们分别由什么样的平面图形旋转而成的
提示:(1)是由矩形绕其中一边所在直线旋转而成.(2)是由直角三角形绕其中一直角边所在直线旋转而成.(3)是由直角梯形绕垂直于底边的腰所在直线旋转而成.(4)是由半圆绕直径所在直线旋转而成.
【概念生成】
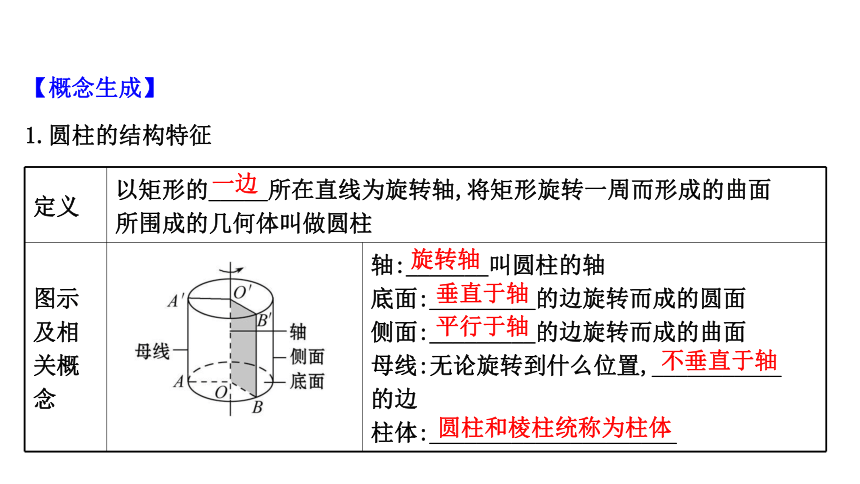
1.圆柱的结构特征
定义 以矩形的_____所在直线为旋转轴,将矩形旋转一周而形成的曲面
所围成的几何体叫做圆柱
图示
及相
关概
念 轴:_______叫圆柱的轴
底面:_________的边旋转而成的圆面
侧面:_________的边旋转而成的曲面
母线:无论旋转到什么位置,___________
的边
柱体:_____________________
一边
旋转轴
垂直于轴
平行于轴
不垂直于轴
圆柱和棱柱统称为柱体
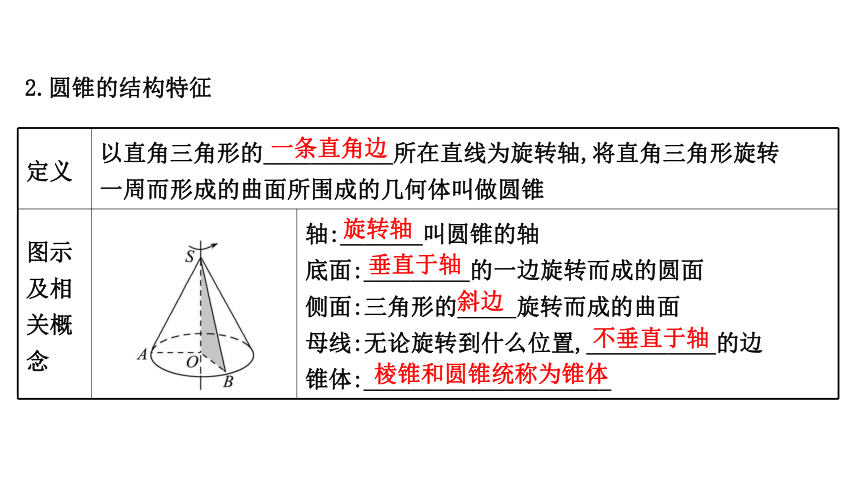
2.圆锥的结构特征
定义 以直角三角形的___________所在直线为旋转轴,将直角三角形旋转
一周而形成的曲面所围成的几何体叫做圆锥
图示
及相
关概
念 轴:_______叫圆锥的轴
底面:_________的一边旋转而成的圆面
侧面:三角形的_____旋转而成的曲面
母线:无论旋转到什么位置,___________的边
锥体:_____________________
一条直角边
旋转轴
垂直于轴
斜边
不垂直于轴
棱锥和圆锥统称为锥体
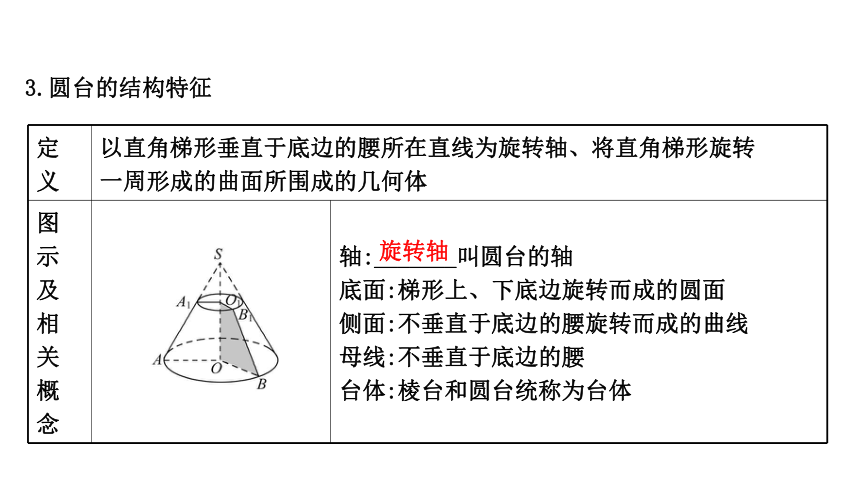
3.圆台的结构特征
定义 以直角梯形垂直于底边的腰所在直线为旋转轴、将直角梯形旋转
一周形成的曲面所围成的几何体
图示
及相
关概
念 轴:_______叫圆台的轴
底面:梯形上、下底边旋转而成的圆面
侧面:不垂直于底边的腰旋转而成的曲线
母线:不垂直于底边的腰
台体:棱台和圆台统称为台体
旋转轴
4.旋转体的概念
类似圆柱、圆锥、圆台的形成方式构成的几何体都是旋转体.
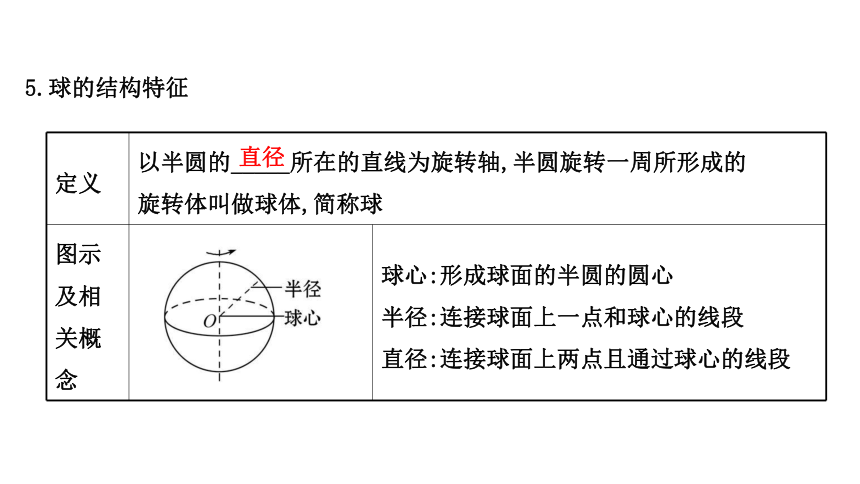
5.球的结构特征
定义 以半圆的_____所在的直线为旋转轴,半圆旋转一周所形成的
旋转体叫做球体,简称球
图示
及相
关概
念 球心:形成球面的半圆的圆心
半径:连接球面上一点和球心的线段
直径:连接球面上两点且通过球心的线段
直径
6.球的表面积
球的表面积公式:S=_____(R为球的半径).
4πR2
核心互动探究
探究点一 旋转体的概念与结构特征
【典例1】1.下列命题中正确的有 ( )
①圆台的所有平行于底面的截面都是圆;②圆台是直角梯形绕其一边旋转一周而成的;③在圆台的上、下底面圆周上各取一点,则这两点的连线一定是圆台的母线;④圆台可看成是平行于底面的平面截圆锥得到的
A.1个 B.2个 C.3个 D.4个
2.直角三角形绕其一边旋转一周所形成的几何体是否一定是圆锥
【思维导引】1.根据圆台的有关概念判断.
2.概念辨析题要紧扣定义,抓准差别进行判断,定义中要求以直角三角形的一条直角边所在直线为轴.
【解析】1.选B.由圆台特点知①④正确;对于②,当这一边是梯形中的一条底边和斜腰时,形成的不是圆台;由圆台的母线延长后交于一点知③错.
2.不一定,当绕其直角边旋转时形成圆锥,当绕其斜边旋转时形成同底的两个圆锥.
【类题通法】
判断旋转体形状的关键
(1)判断旋转体类型的关键是轴的确定,看旋转体是由平面图形绕哪条直线旋转所得,同一个平面图形绕不同的轴旋转,所得的旋转体一般是不同的.
(2)处理旋转体识图问题时,要抓住圆柱和圆锥定义中的关键点:①矩形或直角三角形绕轴旋转形成,其特征是轴所在直线必须与底面垂直;②矩形或直角三角形旋转到任何位置时其形状不能发生变化.
【定向训练】
下列命题中正确的是 ( )
A.直角三角形绕一条边所在直线旋转得到的旋转体是圆锥
B.夹在圆柱的两个平行截面间的几何体还是一个旋转体
C.圆锥截去一个小圆锥后剩余部分是圆台
D.通过圆台侧面上一点,有无数条母线
【解析】选C.选项A错误,应为直角三角形绕其一条直角边所在直线旋转得到的旋转体是圆锥;若绕其斜边所在直线旋转得到的是两个圆锥构成的一个组合体.B错误,没有说明这两个平行截面与底面的位置关系,当这两个平行截面与底面平行时正确,其他情况则是错误的.D错误,通过圆台侧面上一点,只有一条母线.
【补偿训练】
一个有30°角的直角三角板绕其各条边所在直线旋转所得的几何体是圆锥吗 如果以斜边上的高所在的直线为轴旋转180°得到什么图形
【解析】如图①②旋转一周围成的几何体是圆锥,如图③旋转一周所得的几何体是两个圆锥的组合体;如图④旋转180°是两个半圆锥的组合体.
探究点二 旋转体的结构特征及计算
【典例2】一个圆台的母线长为12 cm,两底面面积分别为4π cm2和25π cm2,求圆台的高.
【思维导引】作出圆台的轴截面,是一个等腰梯形.
【解析】圆台的轴截面是等腰梯形ABCD,如图所示.
由已知可得O1A=2 cm,OB=5 cm.
又由题意知,腰长为12 cm,
所以高AM=
【延伸探究】若本例题条件不变,将圆台还原为圆锥后,求圆锥的母线长.
【解析】如图所示,延长BA,OO1,CD,交于点S,
设截得此圆台的圆锥的母线长为l,
则由△SAO1∽△SBO,可得
解得l=20 cm,即截得此圆台的圆锥的母线长为20 cm.
【类题通法】
旋转体截面问题的解题方法
1.用平行于底面的平面去截柱、锥、台等几何体,注意抓住截面的性质(与底面全等或相似),同时结合旋转体中的经过旋转轴的截面(轴截面)的性质,利用相似三角形的性质,构设相关几何变量的方程组,解方程组求得相关几何量是解决旋转体问题的常用方法.
2.圆台(棱台)问题常常要还台为锥解决.
【定向训练】
一个圆锥的高为2,母线与轴的夹角为30°,求圆锥的母线长以及圆锥的轴截面的面积.
【解析】设圆锥的底面圆直径为AB,SO为高,SA为母线,如图所示,则∠ASO=30°.在Rt△SAO中,
AO=SO·tan 30°=2×
而S△ASB= SO·2AO=SO·AO=2×
所以圆锥的母线长为 ,它的轴截面面积为 .
【补偿训练】
将如图所示的直角梯形ABCD绕腰AD所在直线旋转一周得到一个圆台,求截得此圆台的圆锥的高及母线长.
【解析】由题意易知,截得圆台的圆锥的轴截面右半部分如图,
因为∠ECD=∠CBA=45°,所以ED=CD=1,
所以圆锥的高AE=3,则AB=3,
所以母线长BE=3 .
探究点三 球的结构特征及计算
【典例3】半径是13 cm的球面上有A,B,C三点,并且AB=BC=CA=12 cm,试求球心到经过这三点的截面的距离.
【思维导引】解决有关球的计算问题,大都可以归结到球半径,截面圆半径以及球心与截面的圆心为端点的线段所组成的直角三角形中处理.
【解析】设截面圆的圆心为O1,球的球心为O,连接OO1,则OO1为球心到截面的距
离,而O1是正三角形ABC的外心,于是O1A= ×12=4 (cm).在直角△OO1A中,
由勾股定理,得OO1= =11(cm),所以球心到经过A,B,C
三点的截面的距离为11 cm.
【类题通法】
解答与球有关的问题要特别注意抓住:
①球的截面的性质R2=r2+ ;
②球心角、圆心角、圆周角及其关系;
③垂径定理.
【定向训练】
(2020·全国Ⅱ卷)已知△ABC是面积为 的等边三角形,且其顶点都在
球O的球面上.若球O的表面积为16π,则O到平面ABC的距离为 ( )
A. B. C.1 D.
【解析】选C.设△ABC的外接圆圆心为O1,记OO1=d,圆O1的半径为r,球O的半径
为R,△ABC的边长为a,则S△ABC= ,可得a=3,于是r= ,由题知,球O
的表面积为16π,则R=2,由R2=r2+d2易得d=1,即O到平面ABC的距离为1.
【课堂小结】
课堂素养达标
1.如图将图A,B,C,D所示的三角形绕直线l旋转一周,可以得到如图E所示的几何体的是哪一个图中的三角形 ( )
【解析】选B.图E所示的几何体是由两个同底的圆锥叠放在一起形成的组合体,而直角三角形绕着它的一条直角边旋转一周会得到圆锥,图B旋转后符合图E,A,C,D旋转后均不符合.
2.下列命题中,真命题的个数是 ( )
①圆锥的轴截面是所有过顶点的截面中面积最大的一个;
②圆柱的所有平行于底面的截面都是圆面;
③圆台的两个底面可以不平行.
A.0 B.1 C.2 D.3
【解析】选B.①中当圆锥过顶点的轴截面顶角大于90°时,其面积不是最大的;③圆台的两个底面一定平行,故①③错误.
3.用任意一个平面截一个几何体,各个截面都是圆面,则这个几何体一定
是 ( )
A.圆柱
B.圆锥
C.球体
D.圆柱、圆锥、球的组合体
【解析】选C.只有球体被任意一个平面所截,截面是圆面.
4.过球面上两点,可作球的大圆的个数 ( )
A.有且只有一个
B.1个或无数个
C.无数个
D.不存在这种大圆
【解析】选B.当球面上两点的连线过球心时,过这两点的平面可得无数个大圆,当两点的连线不过球心时,球心与这两点不共线,则可确定一个平面截球可得唯一一个大圆.
11.1.5 旋 转 体
新课程标准
素养风向标
1.理解圆柱、圆锥、圆台以及球的概念. .
2.概括并掌握圆柱、圆锥、圆台以及球的结构特征.
1.了解圆柱、圆锥、圆台、球的定义. (数学抽象)
2.掌握圆柱、圆锥、圆台、球的结构特征. (逻辑推理)
3.能够根据圆柱、圆锥、圆台、球的结构特征识别和区分儿何体. (直观想象)
基础预习初探
观察下列实物图,你能说明由该实物图抽象出的几何体与多面体有何不同吗
提示:多面体有棱有侧面,抽象出的几何体没有棱,侧面是一个曲面.
继续探究:
观察下面的几何体,回答下列问题
(1)它们有什么共同点
提示:它们都可以看成是由一个平面图形旋转而生成的.
(2)它们分别由什么样的平面图形旋转而成的
提示:(1)是由矩形绕其中一边所在直线旋转而成.(2)是由直角三角形绕其中一直角边所在直线旋转而成.(3)是由直角梯形绕垂直于底边的腰所在直线旋转而成.(4)是由半圆绕直径所在直线旋转而成.
【概念生成】
1.圆柱的结构特征
定义 以矩形的_____所在直线为旋转轴,将矩形旋转一周而形成的曲面
所围成的几何体叫做圆柱
图示
及相
关概
念 轴:_______叫圆柱的轴
底面:_________的边旋转而成的圆面
侧面:_________的边旋转而成的曲面
母线:无论旋转到什么位置,___________
的边
柱体:_____________________
一边
旋转轴
垂直于轴
平行于轴
不垂直于轴
圆柱和棱柱统称为柱体
2.圆锥的结构特征
定义 以直角三角形的___________所在直线为旋转轴,将直角三角形旋转
一周而形成的曲面所围成的几何体叫做圆锥
图示
及相
关概
念 轴:_______叫圆锥的轴
底面:_________的一边旋转而成的圆面
侧面:三角形的_____旋转而成的曲面
母线:无论旋转到什么位置,___________的边
锥体:_____________________
一条直角边
旋转轴
垂直于轴
斜边
不垂直于轴
棱锥和圆锥统称为锥体
3.圆台的结构特征
定义 以直角梯形垂直于底边的腰所在直线为旋转轴、将直角梯形旋转
一周形成的曲面所围成的几何体
图示
及相
关概
念 轴:_______叫圆台的轴
底面:梯形上、下底边旋转而成的圆面
侧面:不垂直于底边的腰旋转而成的曲线
母线:不垂直于底边的腰
台体:棱台和圆台统称为台体
旋转轴
4.旋转体的概念
类似圆柱、圆锥、圆台的形成方式构成的几何体都是旋转体.
5.球的结构特征
定义 以半圆的_____所在的直线为旋转轴,半圆旋转一周所形成的
旋转体叫做球体,简称球
图示
及相
关概
念 球心:形成球面的半圆的圆心
半径:连接球面上一点和球心的线段
直径:连接球面上两点且通过球心的线段
直径
6.球的表面积
球的表面积公式:S=_____(R为球的半径).
4πR2
核心互动探究
探究点一 旋转体的概念与结构特征
【典例1】1.下列命题中正确的有 ( )
①圆台的所有平行于底面的截面都是圆;②圆台是直角梯形绕其一边旋转一周而成的;③在圆台的上、下底面圆周上各取一点,则这两点的连线一定是圆台的母线;④圆台可看成是平行于底面的平面截圆锥得到的
A.1个 B.2个 C.3个 D.4个
2.直角三角形绕其一边旋转一周所形成的几何体是否一定是圆锥
【思维导引】1.根据圆台的有关概念判断.
2.概念辨析题要紧扣定义,抓准差别进行判断,定义中要求以直角三角形的一条直角边所在直线为轴.
【解析】1.选B.由圆台特点知①④正确;对于②,当这一边是梯形中的一条底边和斜腰时,形成的不是圆台;由圆台的母线延长后交于一点知③错.
2.不一定,当绕其直角边旋转时形成圆锥,当绕其斜边旋转时形成同底的两个圆锥.
【类题通法】
判断旋转体形状的关键
(1)判断旋转体类型的关键是轴的确定,看旋转体是由平面图形绕哪条直线旋转所得,同一个平面图形绕不同的轴旋转,所得的旋转体一般是不同的.
(2)处理旋转体识图问题时,要抓住圆柱和圆锥定义中的关键点:①矩形或直角三角形绕轴旋转形成,其特征是轴所在直线必须与底面垂直;②矩形或直角三角形旋转到任何位置时其形状不能发生变化.
【定向训练】
下列命题中正确的是 ( )
A.直角三角形绕一条边所在直线旋转得到的旋转体是圆锥
B.夹在圆柱的两个平行截面间的几何体还是一个旋转体
C.圆锥截去一个小圆锥后剩余部分是圆台
D.通过圆台侧面上一点,有无数条母线
【解析】选C.选项A错误,应为直角三角形绕其一条直角边所在直线旋转得到的旋转体是圆锥;若绕其斜边所在直线旋转得到的是两个圆锥构成的一个组合体.B错误,没有说明这两个平行截面与底面的位置关系,当这两个平行截面与底面平行时正确,其他情况则是错误的.D错误,通过圆台侧面上一点,只有一条母线.
【补偿训练】
一个有30°角的直角三角板绕其各条边所在直线旋转所得的几何体是圆锥吗 如果以斜边上的高所在的直线为轴旋转180°得到什么图形
【解析】如图①②旋转一周围成的几何体是圆锥,如图③旋转一周所得的几何体是两个圆锥的组合体;如图④旋转180°是两个半圆锥的组合体.
探究点二 旋转体的结构特征及计算
【典例2】一个圆台的母线长为12 cm,两底面面积分别为4π cm2和25π cm2,求圆台的高.
【思维导引】作出圆台的轴截面,是一个等腰梯形.
【解析】圆台的轴截面是等腰梯形ABCD,如图所示.
由已知可得O1A=2 cm,OB=5 cm.
又由题意知,腰长为12 cm,
所以高AM=
【延伸探究】若本例题条件不变,将圆台还原为圆锥后,求圆锥的母线长.
【解析】如图所示,延长BA,OO1,CD,交于点S,
设截得此圆台的圆锥的母线长为l,
则由△SAO1∽△SBO,可得
解得l=20 cm,即截得此圆台的圆锥的母线长为20 cm.
【类题通法】
旋转体截面问题的解题方法
1.用平行于底面的平面去截柱、锥、台等几何体,注意抓住截面的性质(与底面全等或相似),同时结合旋转体中的经过旋转轴的截面(轴截面)的性质,利用相似三角形的性质,构设相关几何变量的方程组,解方程组求得相关几何量是解决旋转体问题的常用方法.
2.圆台(棱台)问题常常要还台为锥解决.
【定向训练】
一个圆锥的高为2,母线与轴的夹角为30°,求圆锥的母线长以及圆锥的轴截面的面积.
【解析】设圆锥的底面圆直径为AB,SO为高,SA为母线,如图所示,则∠ASO=30°.在Rt△SAO中,
AO=SO·tan 30°=2×
而S△ASB= SO·2AO=SO·AO=2×
所以圆锥的母线长为 ,它的轴截面面积为 .
【补偿训练】
将如图所示的直角梯形ABCD绕腰AD所在直线旋转一周得到一个圆台,求截得此圆台的圆锥的高及母线长.
【解析】由题意易知,截得圆台的圆锥的轴截面右半部分如图,
因为∠ECD=∠CBA=45°,所以ED=CD=1,
所以圆锥的高AE=3,则AB=3,
所以母线长BE=3 .
探究点三 球的结构特征及计算
【典例3】半径是13 cm的球面上有A,B,C三点,并且AB=BC=CA=12 cm,试求球心到经过这三点的截面的距离.
【思维导引】解决有关球的计算问题,大都可以归结到球半径,截面圆半径以及球心与截面的圆心为端点的线段所组成的直角三角形中处理.
【解析】设截面圆的圆心为O1,球的球心为O,连接OO1,则OO1为球心到截面的距
离,而O1是正三角形ABC的外心,于是O1A= ×12=4 (cm).在直角△OO1A中,
由勾股定理,得OO1= =11(cm),所以球心到经过A,B,C
三点的截面的距离为11 cm.
【类题通法】
解答与球有关的问题要特别注意抓住:
①球的截面的性质R2=r2+ ;
②球心角、圆心角、圆周角及其关系;
③垂径定理.
【定向训练】
(2020·全国Ⅱ卷)已知△ABC是面积为 的等边三角形,且其顶点都在
球O的球面上.若球O的表面积为16π,则O到平面ABC的距离为 ( )
A. B. C.1 D.
【解析】选C.设△ABC的外接圆圆心为O1,记OO1=d,圆O1的半径为r,球O的半径
为R,△ABC的边长为a,则S△ABC= ,可得a=3,于是r= ,由题知,球O
的表面积为16π,则R=2,由R2=r2+d2易得d=1,即O到平面ABC的距离为1.
【课堂小结】
课堂素养达标
1.如图将图A,B,C,D所示的三角形绕直线l旋转一周,可以得到如图E所示的几何体的是哪一个图中的三角形 ( )
【解析】选B.图E所示的几何体是由两个同底的圆锥叠放在一起形成的组合体,而直角三角形绕着它的一条直角边旋转一周会得到圆锥,图B旋转后符合图E,A,C,D旋转后均不符合.
2.下列命题中,真命题的个数是 ( )
①圆锥的轴截面是所有过顶点的截面中面积最大的一个;
②圆柱的所有平行于底面的截面都是圆面;
③圆台的两个底面可以不平行.
A.0 B.1 C.2 D.3
【解析】选B.①中当圆锥过顶点的轴截面顶角大于90°时,其面积不是最大的;③圆台的两个底面一定平行,故①③错误.
3.用任意一个平面截一个几何体,各个截面都是圆面,则这个几何体一定
是 ( )
A.圆柱
B.圆锥
C.球体
D.圆柱、圆锥、球的组合体
【解析】选C.只有球体被任意一个平面所截,截面是圆面.
4.过球面上两点,可作球的大圆的个数 ( )
A.有且只有一个
B.1个或无数个
C.无数个
D.不存在这种大圆
【解析】选B.当球面上两点的连线过球心时,过这两点的平面可得无数个大圆,当两点的连线不过球心时,球心与这两点不共线,则可确定一个平面截球可得唯一一个大圆.
