11.2平面的基本事实与推论 课件 2020-2021学年高一下学期数学人教B版(2019)必修第四册31张PPT
文档属性
| 名称 | 11.2平面的基本事实与推论 课件 2020-2021学年高一下学期数学人教B版(2019)必修第四册31张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 656.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 09:57:00 | ||
图片预览






文档简介
11.2 平面的基本事实与推论
基础预习初探
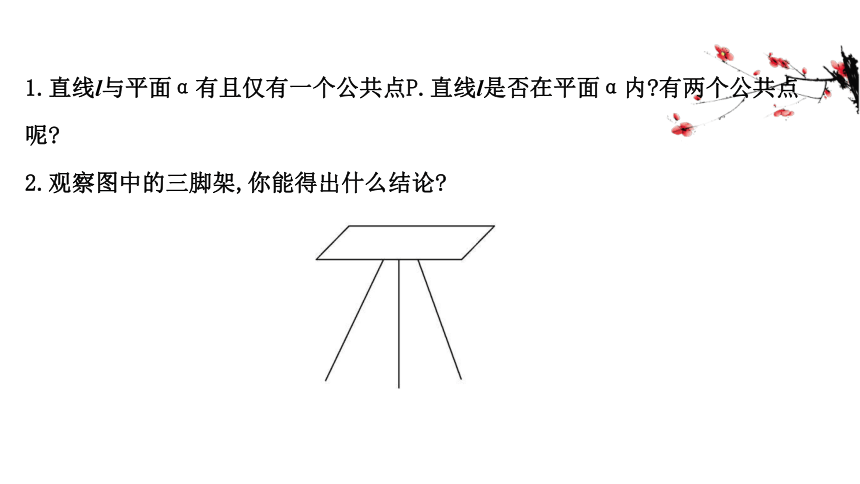
1.直线l与平面α有且仅有一个公共点P.直线l是否在平面α内?有两个公共点呢?
2.观察图中的三脚架,你能得出什么结论?
继续探究:
(1)三点确定一个平面吗?
提示:当三点在一条直线上时,不能确定一个平面,当三点不在同一条直线上时,确定一个平面.
(2)直线和平面都是由点组成的,联系集合的观点,点和直线、平面的位置关系,如何用符号来表示?直线和平面呢?
提示:点和直线、平面的位置关系可用数学符号“∈”或“?”表示,直线和平面的位置关系,可用数学符号 “?”或“?”表示.
【概念生成】
平面的基本事实及推论
基本
事实
内容
图形
符号
基本
事实1
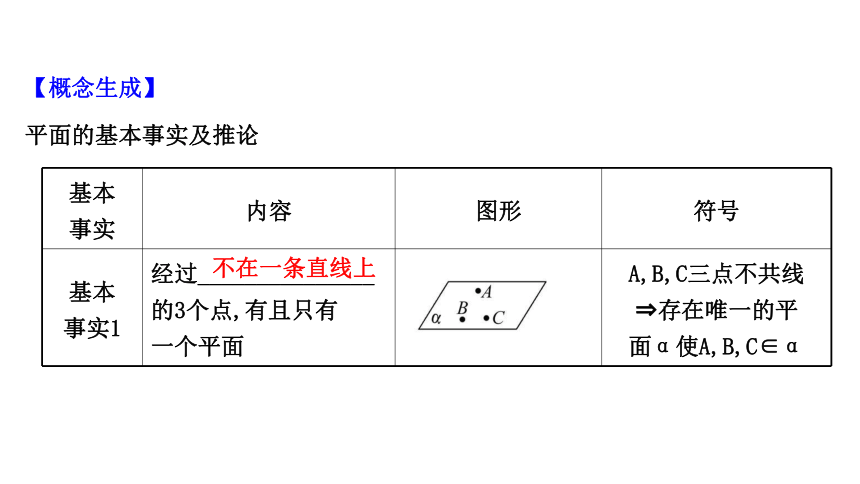
经过_______________
的3个点,有且只有
一个平面
A,B,C三点不共线
?存在唯一的平
面α使A,B,C∈α
不在一条直线上
基本
事实2
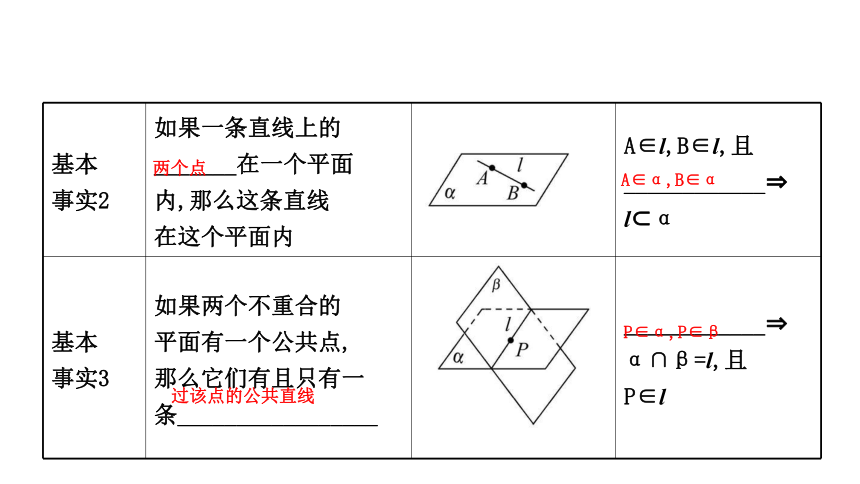
如果一条直线上的
_______在一个平面
内,那么这条直线
在这个平面内
A∈l,B∈l,且
____________?
l?α
基本
事实3
如果两个不重合的
平面有一个公共点,
那么它们有且只有一
条_________________
____________?
α∩β=l,且
P∈l
两个点
过该点的公共直线
A∈α,B∈α
P∈α,P∈β
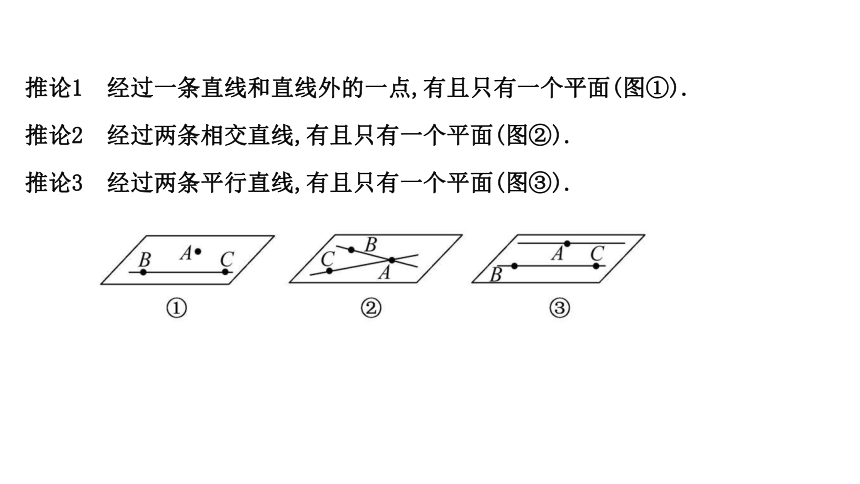
推论1 经过一条直线和直线外的一点,有且只有一个平面(图①).
推论2 经过两条相交直线,有且只有一个平面(图②).
推论3 经过两条平行直线,有且只有一个平面(图③).
核心互动探究
探究点一 文字语言、图形语言、符号语言的相互转化
【典例1】根据下列符号表示的语句,说明点、线、面之间的位置关系,并画出相应的图形:
(1)A∈α,B?α;
(2)l?α,m?α,m∩α=A,A?l;
(3)P∈l,P?α,Q∈l,Q∈α.
【思维导引】解答本题要正确理解立体几何中表示点、线、面之间位置关系的符号“∈”“?”“?”“?”“∩”的意义,在此基础上,由符号表示已知语句,写出相应的点、线、面的位置关系,画出图形.
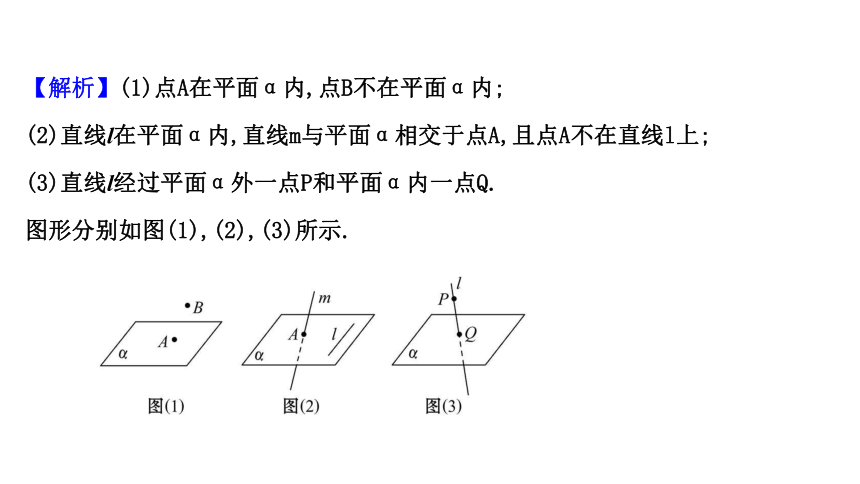
【解析】(1)点A在平面α内,点B不在平面α内;
(2)直线l在平面α内,直线m与平面α相交于点A,且点A不在直线l上;
(3)直线l经过平面α外一点P和平面α内一点Q.
图形分别如图(1),(2),(3)所示.
【类题通法】
文字语言、图形语言、符号语言的应用
1.用文字语言、符号语言表示一个图形时,首先仔细观察图形有几个平面、几条直线且相互之间的位置关系如何,试着用文字语言表示,再用符号语言表示.
2.要注意符号语言的意义.如点与直线的位置关系只能用“∈”或“?”表示,直线与平面的位置关系只能用“?”或“?”表示.
3.由符号语言或文字语言画相应的图形时,要注意实线和虚线的区别.
【定向训练】
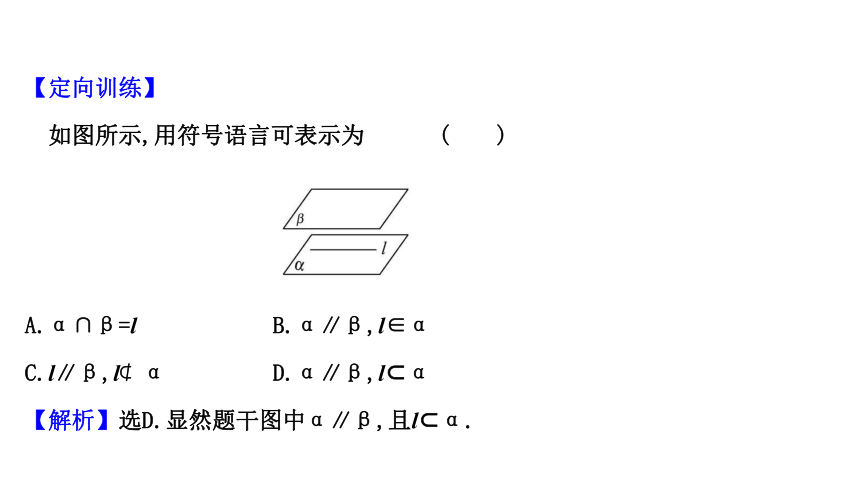
如图所示,用符号语言可表示为 ( )
A.α∩β=l B.α∥β,l∈α
C.l∥β,l?α D.α∥β,l?α
【解析】选D.显然题干图中α∥β,且l?α.
探究点二 点、线共面问题
【典例2】已知四条直线两两相交,且不共点,求证:这四条直线在同一平面内.
【思维导引】四条直线两两相交且不共点,可能有两种情况:一是有三条直线共点;二是任意三条直线都不共点.
【解析】已知:a,b,c,d四条直线两两相交,且不共点,求证:a,b,c,d四线共面.
证明:(1)若a,b,c三线共点于O,如图所示,因为O?d,
所以经过d与点O有且只有一个平面α.
因为A,B,C分别是d与a,b,c的交点,
所以A,B,C三点在平面α内.由基本事实2知a,b,c都在平面α内,故a,b,c,d共面;
(2)若a,b,c,d无三线共点,如图所示,
因为a∩b=A,所以经过a,b有且仅有一个平面α,所以B,C∈α.由基本事实2知c?α.
同理,d?α,从而有a,b,c,d共面.
综上所述,四条直线两两相交,且不共点,这四条直线在同一平面内.
【类题通法】
证明多线共面的两种方法
1.方法一:先由部分直线确定一个平面,再证明其他直线也在这个平面内.
2.方法二:先说明一些直线在一个平面内,另一些直线在另一个平面内,再证明两个平面重合.
【定向训练】
一条直线与三条平行直线都相交,求证:这四条直线共面.
【证明】已知:a∥b∥c,l∩a=A,l∩b=B,l∩c=C.求证:直线a,b,c,l共面.
证明:方法一:因为a∥b,所以a,b确定一个平面α,
因为A∈l,B∈l,且A∈α,B∈α,故l?α.
又因为a∥c,所以a,c确定一个平面β.
同理可证l?β,所以α∩β=a且α∩β=l.
因为过两条相交直线a,l有且只有一个平面,
故α与β重合,即直线a,b,c,l共面.
方法二:由方法一得a,b,l共面α,也就是说b在a,l确定的平面α内.同理可证c在a,l确定的平面α内.因为过a和l只能确定一个平面,所以a,b,c,l共面.
探究点三 交线问题
【典例3】如图,G是正方体ABCD-A1B1C1D1的棱DD1延长线上一点,E,F是棱AB,BC的中点.试分别画出过下列各点、直线的平面与正方体表面的交线:
(1)过点G及AC;
(2)过三点E,F,D1.
【思维导引】找两个平面的两个公共点,则过这两个公共点的直线为两平面的交线.
【解析】(1)画法:连接GA交A1D1于点M;连接GC交C1D1于点N;连接MN,AC,则MA,CN,MN,AC为所求平面与正方体表面的交线.如图①.
(2)画法:连接EF交DC的延长线于点P,交DA的延长线于点Q;连接D1P交CC1于点M,连接D1Q交AA1于点N;连接MF,NE,则D1M,MF,FE,EN,ND1为所求平面与正方体表面的交线.如图②.
【类题通法】
画截面图形的方法
画截面截得正方体的截面图形,关键是利用好三个基本事实,找到两个平面上的公共点是解决此类问题的突破口.
【定向训练】
如图,在棱长是a的正方体ABCD-A1B1C1D1中,M,N分别是AA1,D1C1的中点,过D,M,N三点的平面与正方体的下底面A1B1C1D1相交于直线l:
(1)画出交线l;
(2)设l∩A1B1=P,求PB1的长.
【解析】(1)如图,延长DM,D1A1,交于点Q,则点Q是平面DMN与平面A1B1C1D1的一个公共点.
连接QN,则直线QN就是交线l;
(2)因为M是AA1的中点,MA1∥DD1,
所以A1是QD1的中点.
又A1P∥D1N,所以A1P= D1N.
因为N是D1C1的中点,所以A1P= D1C1= ,
所以PB1=A1B1-A1P= a.
【补偿训练】
在平面α外,△ABC三边所在的直线满足AB∩α=P,BC∩α=Q,AC∩α=R,如图所示.求证:P,Q,R三点共线.
【证明】方法一:因为AB∩α=P,
所以P∈AB,P∈平面α.
又AB?平面ABC,所以P∈平面ABC.
所以由基本事实3可知:点P在平面ABC与平面α的交线上,同理可证Q,R也在平面ABC与平面α的交线上.所以P,Q,R三点共线.
方法二:因为AP∩AR=A,
所以直线AP与直线AR确定平面APR.
又因为AB∩α=P,AC∩α=R,
所以平面APR∩平面α=PR.
因为B∈平面APR,C∈平面APR,所以BC?平面APR.
因为Q∈BC,所以Q∈平面APR,又Q∈α,所以Q∈PR,所以P,Q,R三点共线.
【课堂小结】
课堂素养达标
1.若点A在平面α内,直线a在平面α内,点A不在直线a上,
用符号语言可表示为 ( )
A.A∈α,a?α,A?a
B.A∈α,a∈α,A?a
C.A?α,a?α,A?a
D.A∈α,a?α,A?a
【解析】选A.点与线、面的关系用∈、?;线与面的关系用?、?.B选项中,“a∈α”错误;C选项中“A?α”错误;D选项中“A?a”错误.
2.若两个不重合的平面有公共点,则公共点有 ( )
A.1个
B.2个
C.1个或无数个
D.无数个且在同一条直线上
【解析】选D.利用基本事实3可知如果两个平面有一个公共点,则它们就一定有一条交线,而线是由无数个点构成的,所以这两个平面有无数个在同一直线上的交点.
3.如果直线a?平面α,直线b?平面α,M∈a,N∈b,且M∈l,N∈l,
那么 ( )
A.l?α B.l?α
C.l∩α=M D.l∩α=N
【解析】选A.因为M∈a,N∈b,a,b?α,所以M,N∈α,根据基本事实2可知l?α.
4.由4条平行直线最多可以确定 ( )
A.2个平面 B.4个平面
C.5个平面 D.6个平面
【解析】选D.本题从确定平面的条件来考虑即可,要使四条平行直线确定的平面最多,只有当这四条直线中任两条所确定的平面互不相同时即为最多,从而得到结果.由确定平面的条件知,由4条平行直线最多可以确定6个平面.
基本
事实2
如果一条直线上的
_______在一个平面
内,那么这条直线
在这个平面内
A∈l,B∈l,且
____________?
l?α
基本
事实3
如果两个不重合的
平面有一个公共点,
那么它们有且只有一
条_________________
____________?
α∩β=l,且
P∈l
两个点
过该点的公共直线
A∈α,B∈α
P∈α,P∈β
基础预习初探
1.直线l与平面α有且仅有一个公共点P.直线l是否在平面α内?有两个公共点呢?
2.观察图中的三脚架,你能得出什么结论?
继续探究:
(1)三点确定一个平面吗?
提示:当三点在一条直线上时,不能确定一个平面,当三点不在同一条直线上时,确定一个平面.
(2)直线和平面都是由点组成的,联系集合的观点,点和直线、平面的位置关系,如何用符号来表示?直线和平面呢?
提示:点和直线、平面的位置关系可用数学符号“∈”或“?”表示,直线和平面的位置关系,可用数学符号 “?”或“?”表示.
【概念生成】
平面的基本事实及推论
基本
事实
内容
图形
符号
基本
事实1
经过_______________
的3个点,有且只有
一个平面
A,B,C三点不共线
?存在唯一的平
面α使A,B,C∈α
不在一条直线上
基本
事实2
如果一条直线上的
_______在一个平面
内,那么这条直线
在这个平面内
A∈l,B∈l,且
____________?
l?α
基本
事实3
如果两个不重合的
平面有一个公共点,
那么它们有且只有一
条_________________
____________?
α∩β=l,且
P∈l
两个点
过该点的公共直线
A∈α,B∈α
P∈α,P∈β
推论1 经过一条直线和直线外的一点,有且只有一个平面(图①).
推论2 经过两条相交直线,有且只有一个平面(图②).
推论3 经过两条平行直线,有且只有一个平面(图③).
核心互动探究
探究点一 文字语言、图形语言、符号语言的相互转化
【典例1】根据下列符号表示的语句,说明点、线、面之间的位置关系,并画出相应的图形:
(1)A∈α,B?α;
(2)l?α,m?α,m∩α=A,A?l;
(3)P∈l,P?α,Q∈l,Q∈α.
【思维导引】解答本题要正确理解立体几何中表示点、线、面之间位置关系的符号“∈”“?”“?”“?”“∩”的意义,在此基础上,由符号表示已知语句,写出相应的点、线、面的位置关系,画出图形.
【解析】(1)点A在平面α内,点B不在平面α内;
(2)直线l在平面α内,直线m与平面α相交于点A,且点A不在直线l上;
(3)直线l经过平面α外一点P和平面α内一点Q.
图形分别如图(1),(2),(3)所示.
【类题通法】
文字语言、图形语言、符号语言的应用
1.用文字语言、符号语言表示一个图形时,首先仔细观察图形有几个平面、几条直线且相互之间的位置关系如何,试着用文字语言表示,再用符号语言表示.
2.要注意符号语言的意义.如点与直线的位置关系只能用“∈”或“?”表示,直线与平面的位置关系只能用“?”或“?”表示.
3.由符号语言或文字语言画相应的图形时,要注意实线和虚线的区别.
【定向训练】
如图所示,用符号语言可表示为 ( )
A.α∩β=l B.α∥β,l∈α
C.l∥β,l?α D.α∥β,l?α
【解析】选D.显然题干图中α∥β,且l?α.
探究点二 点、线共面问题
【典例2】已知四条直线两两相交,且不共点,求证:这四条直线在同一平面内.
【思维导引】四条直线两两相交且不共点,可能有两种情况:一是有三条直线共点;二是任意三条直线都不共点.
【解析】已知:a,b,c,d四条直线两两相交,且不共点,求证:a,b,c,d四线共面.
证明:(1)若a,b,c三线共点于O,如图所示,因为O?d,
所以经过d与点O有且只有一个平面α.
因为A,B,C分别是d与a,b,c的交点,
所以A,B,C三点在平面α内.由基本事实2知a,b,c都在平面α内,故a,b,c,d共面;
(2)若a,b,c,d无三线共点,如图所示,
因为a∩b=A,所以经过a,b有且仅有一个平面α,所以B,C∈α.由基本事实2知c?α.
同理,d?α,从而有a,b,c,d共面.
综上所述,四条直线两两相交,且不共点,这四条直线在同一平面内.
【类题通法】
证明多线共面的两种方法
1.方法一:先由部分直线确定一个平面,再证明其他直线也在这个平面内.
2.方法二:先说明一些直线在一个平面内,另一些直线在另一个平面内,再证明两个平面重合.
【定向训练】
一条直线与三条平行直线都相交,求证:这四条直线共面.
【证明】已知:a∥b∥c,l∩a=A,l∩b=B,l∩c=C.求证:直线a,b,c,l共面.
证明:方法一:因为a∥b,所以a,b确定一个平面α,
因为A∈l,B∈l,且A∈α,B∈α,故l?α.
又因为a∥c,所以a,c确定一个平面β.
同理可证l?β,所以α∩β=a且α∩β=l.
因为过两条相交直线a,l有且只有一个平面,
故α与β重合,即直线a,b,c,l共面.
方法二:由方法一得a,b,l共面α,也就是说b在a,l确定的平面α内.同理可证c在a,l确定的平面α内.因为过a和l只能确定一个平面,所以a,b,c,l共面.
探究点三 交线问题
【典例3】如图,G是正方体ABCD-A1B1C1D1的棱DD1延长线上一点,E,F是棱AB,BC的中点.试分别画出过下列各点、直线的平面与正方体表面的交线:
(1)过点G及AC;
(2)过三点E,F,D1.
【思维导引】找两个平面的两个公共点,则过这两个公共点的直线为两平面的交线.
【解析】(1)画法:连接GA交A1D1于点M;连接GC交C1D1于点N;连接MN,AC,则MA,CN,MN,AC为所求平面与正方体表面的交线.如图①.
(2)画法:连接EF交DC的延长线于点P,交DA的延长线于点Q;连接D1P交CC1于点M,连接D1Q交AA1于点N;连接MF,NE,则D1M,MF,FE,EN,ND1为所求平面与正方体表面的交线.如图②.
【类题通法】
画截面图形的方法
画截面截得正方体的截面图形,关键是利用好三个基本事实,找到两个平面上的公共点是解决此类问题的突破口.
【定向训练】
如图,在棱长是a的正方体ABCD-A1B1C1D1中,M,N分别是AA1,D1C1的中点,过D,M,N三点的平面与正方体的下底面A1B1C1D1相交于直线l:
(1)画出交线l;
(2)设l∩A1B1=P,求PB1的长.
【解析】(1)如图,延长DM,D1A1,交于点Q,则点Q是平面DMN与平面A1B1C1D1的一个公共点.
连接QN,则直线QN就是交线l;
(2)因为M是AA1的中点,MA1∥DD1,
所以A1是QD1的中点.
又A1P∥D1N,所以A1P= D1N.
因为N是D1C1的中点,所以A1P= D1C1= ,
所以PB1=A1B1-A1P= a.
【补偿训练】
在平面α外,△ABC三边所在的直线满足AB∩α=P,BC∩α=Q,AC∩α=R,如图所示.求证:P,Q,R三点共线.
【证明】方法一:因为AB∩α=P,
所以P∈AB,P∈平面α.
又AB?平面ABC,所以P∈平面ABC.
所以由基本事实3可知:点P在平面ABC与平面α的交线上,同理可证Q,R也在平面ABC与平面α的交线上.所以P,Q,R三点共线.
方法二:因为AP∩AR=A,
所以直线AP与直线AR确定平面APR.
又因为AB∩α=P,AC∩α=R,
所以平面APR∩平面α=PR.
因为B∈平面APR,C∈平面APR,所以BC?平面APR.
因为Q∈BC,所以Q∈平面APR,又Q∈α,所以Q∈PR,所以P,Q,R三点共线.
【课堂小结】
课堂素养达标
1.若点A在平面α内,直线a在平面α内,点A不在直线a上,
用符号语言可表示为 ( )
A.A∈α,a?α,A?a
B.A∈α,a∈α,A?a
C.A?α,a?α,A?a
D.A∈α,a?α,A?a
【解析】选A.点与线、面的关系用∈、?;线与面的关系用?、?.B选项中,“a∈α”错误;C选项中“A?α”错误;D选项中“A?a”错误.
2.若两个不重合的平面有公共点,则公共点有 ( )
A.1个
B.2个
C.1个或无数个
D.无数个且在同一条直线上
【解析】选D.利用基本事实3可知如果两个平面有一个公共点,则它们就一定有一条交线,而线是由无数个点构成的,所以这两个平面有无数个在同一直线上的交点.
3.如果直线a?平面α,直线b?平面α,M∈a,N∈b,且M∈l,N∈l,
那么 ( )
A.l?α B.l?α
C.l∩α=M D.l∩α=N
【解析】选A.因为M∈a,N∈b,a,b?α,所以M,N∈α,根据基本事实2可知l?α.
4.由4条平行直线最多可以确定 ( )
A.2个平面 B.4个平面
C.5个平面 D.6个平面
【解析】选D.本题从确定平面的条件来考虑即可,要使四条平行直线确定的平面最多,只有当这四条直线中任两条所确定的平面互不相同时即为最多,从而得到结果.由确定平面的条件知,由4条平行直线最多可以确定6个平面.
基本
事实2
如果一条直线上的
_______在一个平面
内,那么这条直线
在这个平面内
A∈l,B∈l,且
____________?
l?α
基本
事实3
如果两个不重合的
平面有一个公共点,
那么它们有且只有一
条_________________
____________?
α∩β=l,且
P∈l
两个点
过该点的公共直线
A∈α,B∈α
P∈α,P∈β
