11.3.2直线与平面平行 课件 2020-2021学年高一下学期数学人教B版(2019)必修第四册31张PPT
文档属性
| 名称 | 11.3.2直线与平面平行 课件 2020-2021学年高一下学期数学人教B版(2019)必修第四册31张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 802.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 09:57:50 | ||
图片预览






文档简介
11.3.2 直线与平面平行
基础预习初探
1.观察我们的教室,教室的墙面、地面、天花板均可抽象成平面,把日光灯抽象成一条直线,那么日光灯所在直线与墙面、地面、天花板有何位置关系?
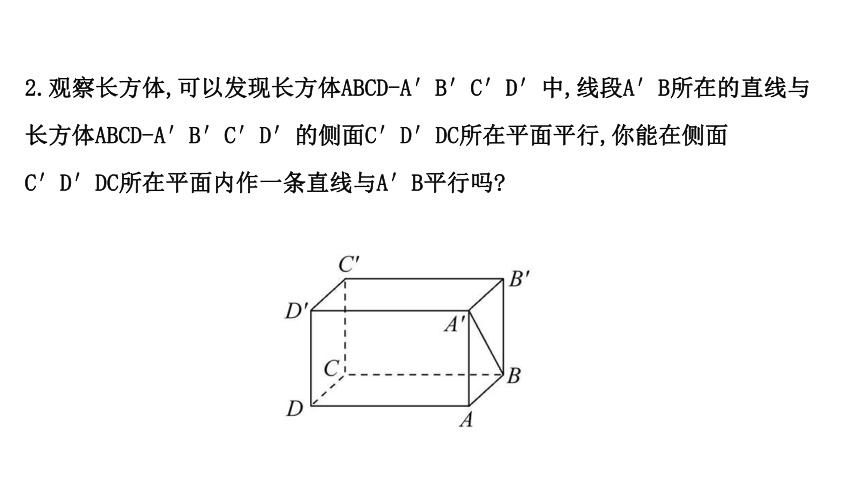
2.观察长方体,可以发现长方体ABCD-A′B′C′D′中,线段A′B所在的直线与长方体ABCD-A′B′C′D′的侧面C′D′DC所在平面平行,你能在侧面C′D′DC所在平面内作一条直线与A′B平行吗?
继续探究:
1.将一本书平放在桌面上,翻动书的封面,假设封面边缘为AB,那么请思考以下两个问题:
(1)翻转中你发现了哪些变化和哪些关系?
提示:翻转的过程其实是以装订边为轴的一个绕轴运动,转动过程中始终AB∥装订边.
(2)AB所在的直线与桌面所在的平面有什么样的位置关系呢?
提示:AB所在的直线与桌面所在的平面平行或AB在桌面所在平面内.
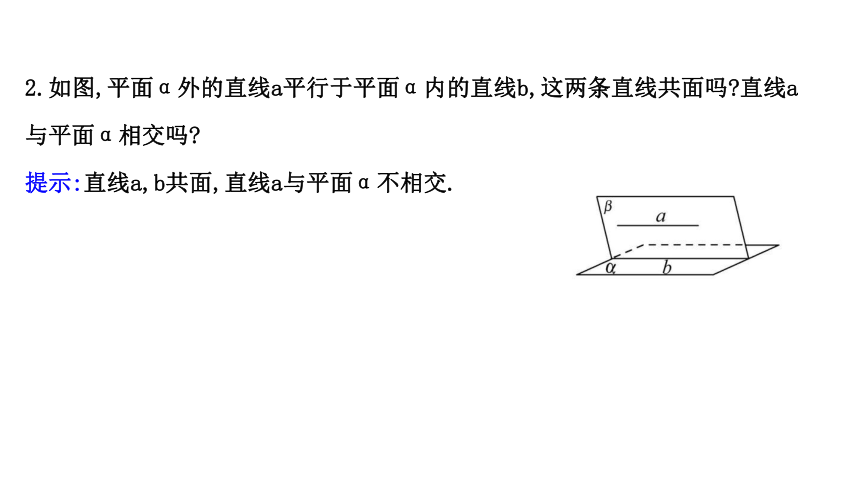
2.如图,平面α外的直线a平行于平面α内的直线b,这两条直线共面吗?直线a与平面α相交吗?
提示:直线a,b共面,直线a与平面α不相交.
【概念生成】
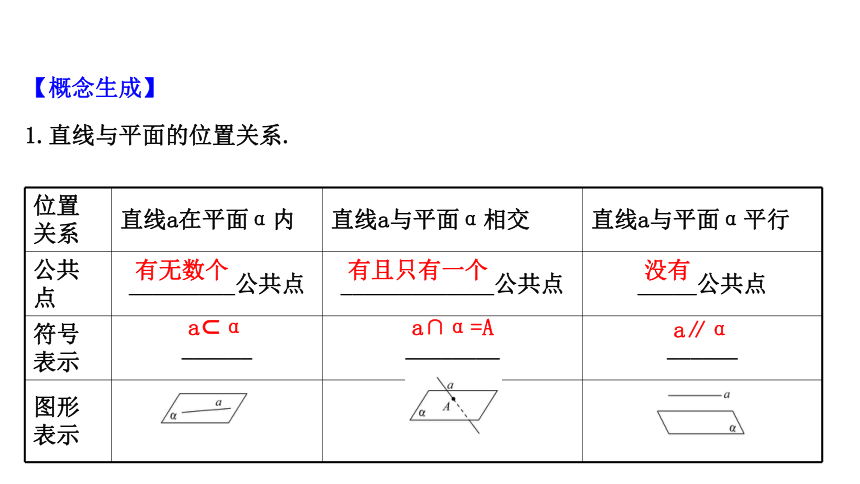
1.直线与平面的位置关系.
位置
关系
直线a在平面α内
直线a与平面α相交
直线a与平面α平行
公共点
_________公共点
_____________公共点
_____公共点
符号
表示
______
________
______
图形
表示
有无数个
有且只有一个
没有
a?α
a∩α=A
a∥α
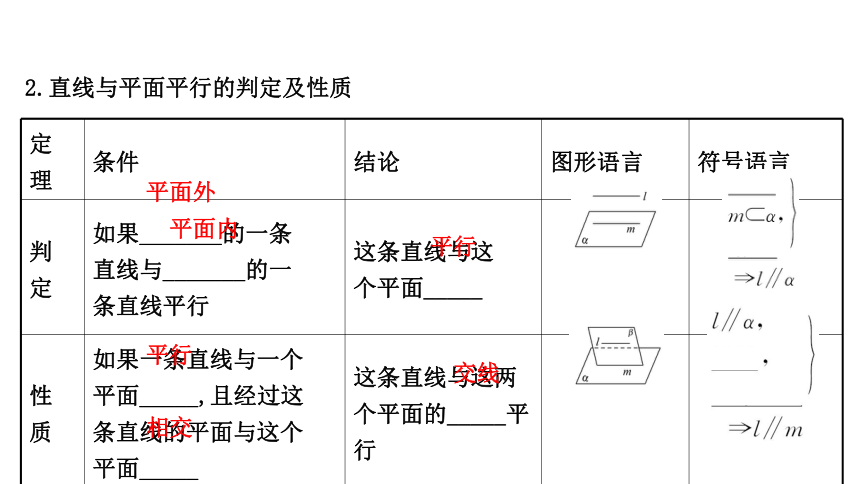
2.直线与平面平行的判定及性质
定理
条件
结论
图形语言
符号语言
判定
如果_______的一条
直线与_______的一
条直线平行
这条直线与这
个平面_____
性质
如果一条直线与一个
平面_____,且经过这
条直线的平面与这个
平面_____
这条直线与这两个平面的_____平行
平面外
平面内
平行
平行
相交
交线
核心互动探究
探究点一 线面平行的判定
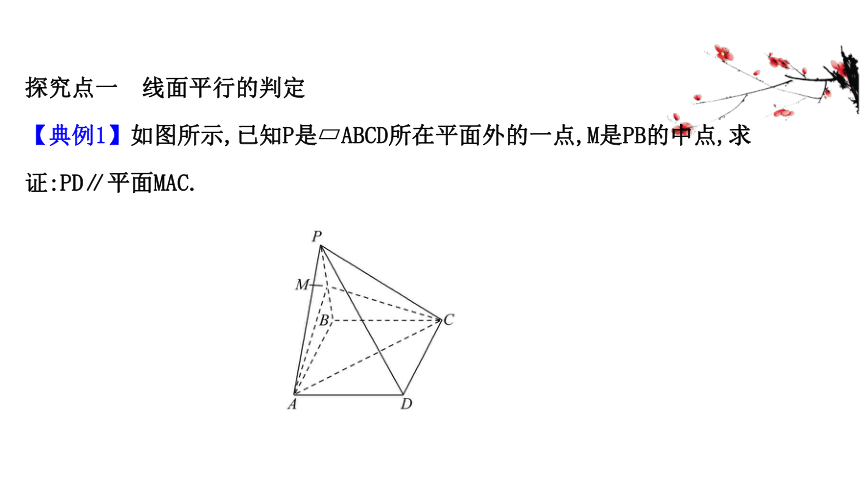
【典例1】如图所示,已知P是?ABCD所在平面外的一点,M是PB的中点,求证:PD∥平面MAC.
【思维导引】要证明直线a与平面α平行的关键是在平面α内找一条直线b,使a∥b.考虑是否有已知的平行线,若无已知的平行线,则根据已知条件作出平行线(有中点常作中位线).
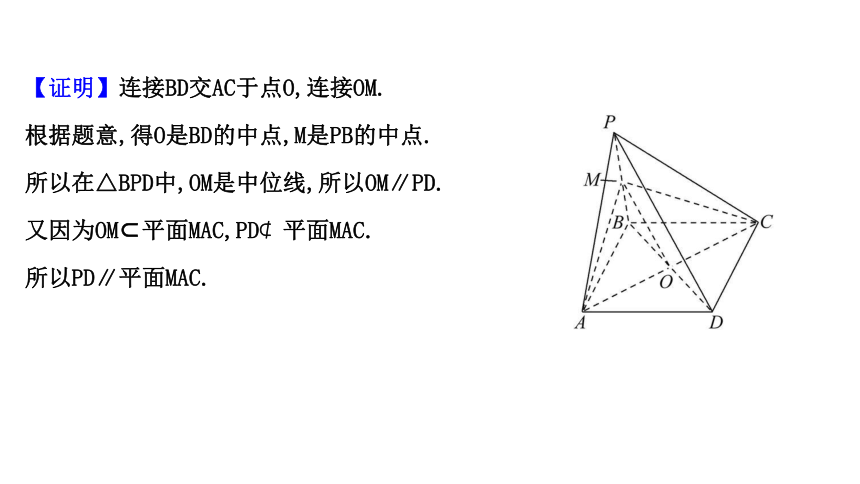
【证明】连接BD交AC于点O,连接OM.
根据题意,得O是BD的中点,M是PB的中点.
所以在△BPD中,OM是中位线,所以OM∥PD.
又因为OM?平面MAC,PD?平面MAC.
所以PD∥平面MAC.
【类题通法】
1.判定直线与平面平行的常用方法
(1)定义法:证明直线与平面没有公共点,通常要借助反证法来证明.
(2)判定定理法:由线线平行证明线面平行.
2.用直线与平面平行的判定定理证明线面平行
(1)基本步骤:
(2)上面的第一步是证题的关键,其常用方法有:①利用三角形中位线、梯形中位线的性质;②利用平行四边形的性质等.
提醒:在证明线面平行时,一定要说明一条直线在平面内,一条直线在平面外,这样才可以得到结论.
【定向训练】
如图,已知在正方体ABCD-A1B1C1D1中,O是底面ABCD对角线的交点,
求证:C1O∥平面AB1D1.
【证明】连接A1C1交B1D1于点O1,连接AO1,
因为O,O1分别为正方体面对角线AC,A1C1的中点,
所以AO平行且等于C1O1,
所以四边形AOC1O1是平行四边形,所以C1O∥AO1.
又因为C1O?平面AB1D1,AO1?平面AB1D1,
所以C1O∥平面AB1D1.
【补偿训练】
若M,N分别是△ABC边AB,AC的中点,MN与过直线BC的平面β的位置关系是 ( )
A.MN∥β
B.MN与β相交或MN?β
C.MN∥β或MN?β
D.MN∥β或MN与β相交或MN?β
【解析】选C.MN是△ABC的中位线,
所以MN∥BC.因为平面β过直线BC,
若平面β过直线MN,则MN?β.
若平面β不过直线MN,由线面平行的判定定理可知MN∥β.
探究点二 线面平行的应用
【典例2】如图所示,用平行于四面体ABCD一组对棱AB,CD的平面截此四面体,求证:截面MNPQ是平行四边形.
【思维导引】应用线面平行的性质定理.
【证明】因为AB∥平面MNPQ,
平面ABC∩平面MNPQ=MN,且AB?平面ABC,
所以由线面平行的性质定理知AB∥MN.
同理AB∥PQ,所以MN∥PQ.
同理可得MQ∥NP.
所以截面MNPQ是平行四边形.
【延伸探究】
1.若本例题条件不变,求证: .
【证明】因为AB∥平面MNPQ,
平面ABC∩平面MNPQ=MN,且AB?平面ABC,
所以由线面平行的性质定理知AB∥MN.
同理AB∥PQ,所以 .
又QM∥DC,所以 ,所以 .
2.若本例中添加条件:AB⊥CD,AB=10,CD=8,且BP∶PD=1∶1,求四边形MNPQ的面积.
【解析】由【典例2】解析知,四边形MNPQ是平行四边形.
因为AB⊥CD,又因为AB∥QP,CD∥MQ,所以PQ⊥QM,
所以四边形MNPQ是矩形.
又BP∶PD=1∶1,所以PQ= BA=5,QM= DC=4,
所以四边形MNPQ的面积为5×4=20.
【类题通法】
线面平行的应用
判定定理与性质定理常常交替使用,即先通过线线平行推出线面平行,再通过线面平行推出线线平行,复杂的题目还可以继续推下去,我们可称它为平行链,如下:
【定向训练】
如图所示,已知E,F,G,H分别为空间四边形ABCD的边AB,BC,CD,DA上的点,且EH∥FG.求证:EH∥BD.
【证明】因为EH∥FG,EH?平面BCD,FG?平面BCD,
所以EH∥平面BCD,
又因为EH?平面ABD,
平面ABD∩平面BCD=BD,所以EH∥BD.
【补偿训练】
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,N是PB的中点,过A,N,D三点的平面交PC于点M,求证:AD∥MN.
【证明】因为四边形ABCD为平行四边形,所以AD∥BC,
又BC?平面PBC,AD?平面PBC,
所以AD∥平面PBC,
又AD?平面ADMN,平面PBC∩平面ADMN=MN,
所以AD∥MN.
【课堂小结】
课堂素养达标
1.直线在平面外是指 ( )
A.直线与平面没有公共点
B.直线与平面相交
C.直线与平面平行
D.直线与平面最多有一个公共点
【解析】选D.直线在平面外是指直线与平面相交或直线与平面平行.
2.b是平面α外的一条直线,可以推出b∥α的条件是 ( )
A.b与α内的一条直线不相交
B.b与α内的两条直线不相交
C.b与α内的无数条直线不相交
D.b与α内的任何一条直线都不相交
【解析】选D.因为b∥α,所以b与α无公共点,从而b与α内任何一条直线无公共点.
3.如图,E,F分别为三棱锥A-BCD的棱BC,BA上的点,且BE∶BC=BF∶BA=1∶3,则直线EF与平面ACD的位置关系是__________.?
【解析】因为BE∶BC=BF∶BA=1∶3,所以EF∥AC.
又EF?平面ACD,AC?平面ACD,所以EF∥平面ACD.
答案:平行
基础预习初探
1.观察我们的教室,教室的墙面、地面、天花板均可抽象成平面,把日光灯抽象成一条直线,那么日光灯所在直线与墙面、地面、天花板有何位置关系?
2.观察长方体,可以发现长方体ABCD-A′B′C′D′中,线段A′B所在的直线与长方体ABCD-A′B′C′D′的侧面C′D′DC所在平面平行,你能在侧面C′D′DC所在平面内作一条直线与A′B平行吗?
继续探究:
1.将一本书平放在桌面上,翻动书的封面,假设封面边缘为AB,那么请思考以下两个问题:
(1)翻转中你发现了哪些变化和哪些关系?
提示:翻转的过程其实是以装订边为轴的一个绕轴运动,转动过程中始终AB∥装订边.
(2)AB所在的直线与桌面所在的平面有什么样的位置关系呢?
提示:AB所在的直线与桌面所在的平面平行或AB在桌面所在平面内.
2.如图,平面α外的直线a平行于平面α内的直线b,这两条直线共面吗?直线a与平面α相交吗?
提示:直线a,b共面,直线a与平面α不相交.
【概念生成】
1.直线与平面的位置关系.
位置
关系
直线a在平面α内
直线a与平面α相交
直线a与平面α平行
公共点
_________公共点
_____________公共点
_____公共点
符号
表示
______
________
______
图形
表示
有无数个
有且只有一个
没有
a?α
a∩α=A
a∥α
2.直线与平面平行的判定及性质
定理
条件
结论
图形语言
符号语言
判定
如果_______的一条
直线与_______的一
条直线平行
这条直线与这
个平面_____
性质
如果一条直线与一个
平面_____,且经过这
条直线的平面与这个
平面_____
这条直线与这两个平面的_____平行
平面外
平面内
平行
平行
相交
交线
核心互动探究
探究点一 线面平行的判定
【典例1】如图所示,已知P是?ABCD所在平面外的一点,M是PB的中点,求证:PD∥平面MAC.
【思维导引】要证明直线a与平面α平行的关键是在平面α内找一条直线b,使a∥b.考虑是否有已知的平行线,若无已知的平行线,则根据已知条件作出平行线(有中点常作中位线).
【证明】连接BD交AC于点O,连接OM.
根据题意,得O是BD的中点,M是PB的中点.
所以在△BPD中,OM是中位线,所以OM∥PD.
又因为OM?平面MAC,PD?平面MAC.
所以PD∥平面MAC.
【类题通法】
1.判定直线与平面平行的常用方法
(1)定义法:证明直线与平面没有公共点,通常要借助反证法来证明.
(2)判定定理法:由线线平行证明线面平行.
2.用直线与平面平行的判定定理证明线面平行
(1)基本步骤:
(2)上面的第一步是证题的关键,其常用方法有:①利用三角形中位线、梯形中位线的性质;②利用平行四边形的性质等.
提醒:在证明线面平行时,一定要说明一条直线在平面内,一条直线在平面外,这样才可以得到结论.
【定向训练】
如图,已知在正方体ABCD-A1B1C1D1中,O是底面ABCD对角线的交点,
求证:C1O∥平面AB1D1.
【证明】连接A1C1交B1D1于点O1,连接AO1,
因为O,O1分别为正方体面对角线AC,A1C1的中点,
所以AO平行且等于C1O1,
所以四边形AOC1O1是平行四边形,所以C1O∥AO1.
又因为C1O?平面AB1D1,AO1?平面AB1D1,
所以C1O∥平面AB1D1.
【补偿训练】
若M,N分别是△ABC边AB,AC的中点,MN与过直线BC的平面β的位置关系是 ( )
A.MN∥β
B.MN与β相交或MN?β
C.MN∥β或MN?β
D.MN∥β或MN与β相交或MN?β
【解析】选C.MN是△ABC的中位线,
所以MN∥BC.因为平面β过直线BC,
若平面β过直线MN,则MN?β.
若平面β不过直线MN,由线面平行的判定定理可知MN∥β.
探究点二 线面平行的应用
【典例2】如图所示,用平行于四面体ABCD一组对棱AB,CD的平面截此四面体,求证:截面MNPQ是平行四边形.
【思维导引】应用线面平行的性质定理.
【证明】因为AB∥平面MNPQ,
平面ABC∩平面MNPQ=MN,且AB?平面ABC,
所以由线面平行的性质定理知AB∥MN.
同理AB∥PQ,所以MN∥PQ.
同理可得MQ∥NP.
所以截面MNPQ是平行四边形.
【延伸探究】
1.若本例题条件不变,求证: .
【证明】因为AB∥平面MNPQ,
平面ABC∩平面MNPQ=MN,且AB?平面ABC,
所以由线面平行的性质定理知AB∥MN.
同理AB∥PQ,所以 .
又QM∥DC,所以 ,所以 .
2.若本例中添加条件:AB⊥CD,AB=10,CD=8,且BP∶PD=1∶1,求四边形MNPQ的面积.
【解析】由【典例2】解析知,四边形MNPQ是平行四边形.
因为AB⊥CD,又因为AB∥QP,CD∥MQ,所以PQ⊥QM,
所以四边形MNPQ是矩形.
又BP∶PD=1∶1,所以PQ= BA=5,QM= DC=4,
所以四边形MNPQ的面积为5×4=20.
【类题通法】
线面平行的应用
判定定理与性质定理常常交替使用,即先通过线线平行推出线面平行,再通过线面平行推出线线平行,复杂的题目还可以继续推下去,我们可称它为平行链,如下:
【定向训练】
如图所示,已知E,F,G,H分别为空间四边形ABCD的边AB,BC,CD,DA上的点,且EH∥FG.求证:EH∥BD.
【证明】因为EH∥FG,EH?平面BCD,FG?平面BCD,
所以EH∥平面BCD,
又因为EH?平面ABD,
平面ABD∩平面BCD=BD,所以EH∥BD.
【补偿训练】
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,N是PB的中点,过A,N,D三点的平面交PC于点M,求证:AD∥MN.
【证明】因为四边形ABCD为平行四边形,所以AD∥BC,
又BC?平面PBC,AD?平面PBC,
所以AD∥平面PBC,
又AD?平面ADMN,平面PBC∩平面ADMN=MN,
所以AD∥MN.
【课堂小结】
课堂素养达标
1.直线在平面外是指 ( )
A.直线与平面没有公共点
B.直线与平面相交
C.直线与平面平行
D.直线与平面最多有一个公共点
【解析】选D.直线在平面外是指直线与平面相交或直线与平面平行.
2.b是平面α外的一条直线,可以推出b∥α的条件是 ( )
A.b与α内的一条直线不相交
B.b与α内的两条直线不相交
C.b与α内的无数条直线不相交
D.b与α内的任何一条直线都不相交
【解析】选D.因为b∥α,所以b与α无公共点,从而b与α内任何一条直线无公共点.
3.如图,E,F分别为三棱锥A-BCD的棱BC,BA上的点,且BE∶BC=BF∶BA=1∶3,则直线EF与平面ACD的位置关系是__________.?
【解析】因为BE∶BC=BF∶BA=1∶3,所以EF∥AC.
又EF?平面ACD,AC?平面ACD,所以EF∥平面ACD.
答案:平行
