11.3.1平行直线与异面直线 课件 2020-2021学年高一下学期数学人教B版(2019)必修第四册 41张PPT
文档属性
| 名称 | 11.3.1平行直线与异面直线 课件 2020-2021学年高一下学期数学人教B版(2019)必修第四册 41张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 699.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 00:00:00 | ||
图片预览









文档简介
11.3 空间中的平行关系
11.3.1 平行直线与异面直线
基础预习初探
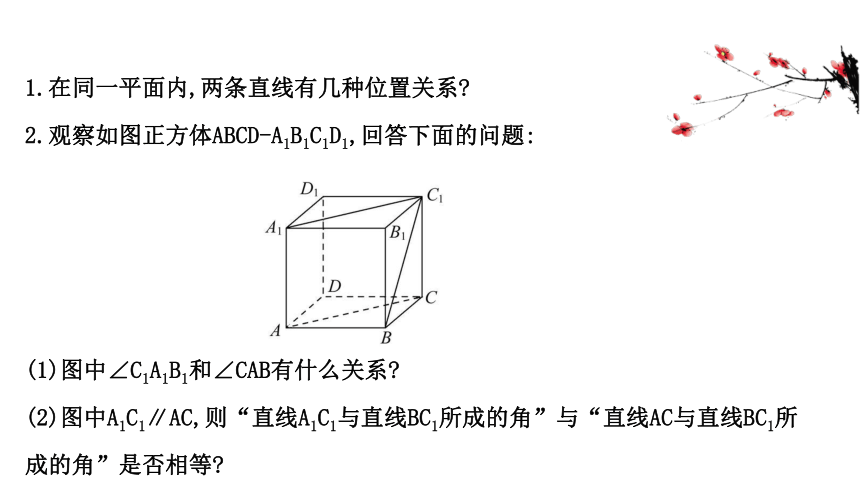
1.在同一平面内,两条直线有几种位置关系?
2.观察如图正方体ABCD-A1B1C1D1,回答下面的问题:
(1)图中∠C1A1B1和∠CAB有什么关系?
(2)图中A1C1∥AC,则“直线A1C1与直线BC1所成的角”与“直线AC与直线BC1所成的角”是否相等?
继续探究:
1.空间中,没有公共点的两条直线一定平行吗?
提示:不一定,在平面内没有公共点的两条直线平行,在空间没有公共点的两条直线可能平行,也可能异面.
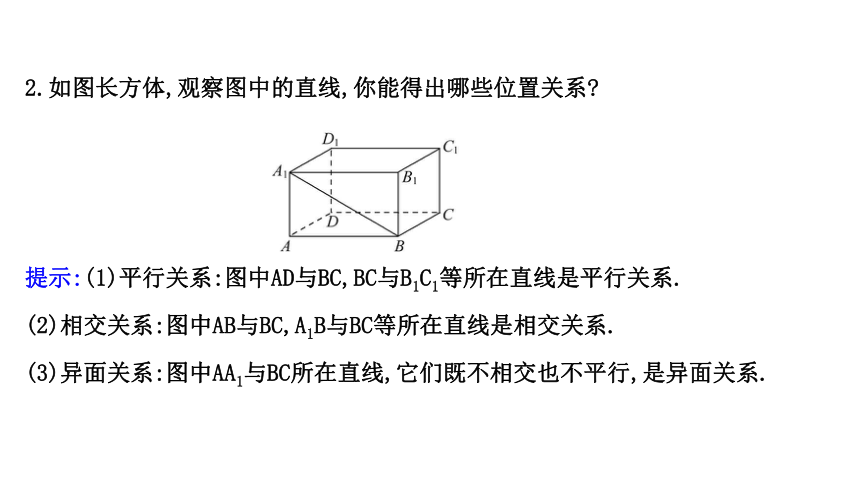
2.如图长方体,观察图中的直线,你能得出哪些位置关系?
提示:(1)平行关系:图中AD与BC,BC与B1C1等所在直线是平行关系.
(2)相交关系:图中AB与BC,A1B与BC等所在直线是相交关系.
(3)异面关系:图中AA1与BC所在直线,它们既不相交也不平行,是异面关系.
【概念生成】
1.平行直线
(1)过直线外一点_____________直线与已知直线平行;
(2)平行直线的传递性:平行于同一条直线的两条直线_________.这一性质
叫做空间平行线的_______.
符号表述: ?b∥c.
(3)等角定理
如果一个角的两边与另一个角的两边分别_________,并且方向_____,那么
这两个角_____.
有且只有一条
互相平行
传递性
对应平行
相同
相等
2.异面直线
(1)画法:如图,为了表示异面直线a,b不共面的特点,作图时,通常用一个或两个平面衬托.
(2)判定:
与一个平面相交于一点的直线与这个平面内___________的直线异面.
不经过交点
3.空间四边形
顺次连接_______的4点所构成的图形,称为空间四边形.其中4个点都是空间四
边形的_____;连接相邻顶点间的线段称为空间四边形的___;连接不相邻顶点间
的线段称为空间四边形的_______.空间四边形用表示顶点的4个字母表示.
不共面
顶点
对角线
边
核心互动探究
探究点一 等角定理的应用
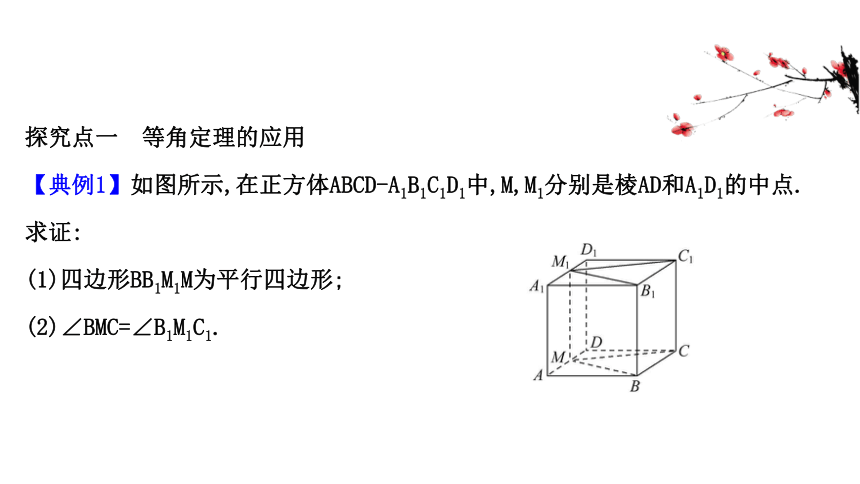
【典例1】如图所示,在正方体ABCD-A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.求证:
(1)四边形BB1M1M为平行四边形;
(2)∠BMC=∠B1M1C1.
【思维导引】(1)欲证四边形BB1M1M是平行四边形,可证其一组对边平行且相等;(2)可结合(1)利用等角定理证明或利用三角形全等证明.
【证明】(1)因为ABCD-A1B1C1D1为正方体.
所以AD=A1D1,且AD∥A1D1,
又M,M1分别为棱AD,A1D1的中点,
所以AM=A1M1且AM∥A1M1,
所以四边形AMM1A1为平行四边形,
所以MM1=AA1且MM1∥AA1.
又AA1=BB1且AA1∥BB1,
所以MM1=BB1且MM1∥BB1,
所以四边形BB1M1M为平行四边形;
(2)方法一:由(1)知四边形BB1M1M为平行四边形,
所以B1M1∥BM.同理可得四边形CC1M1M为平行四边形,所以C1M1∥CM.
因为∠BMC和∠B1M1C1方向相同,
所以∠BMC=∠B1M1C1.
方法二:由(1)知四边形BB1M1M为平行四边形,
所以B1M1=BM.
同理可得四边形CC1M1M为平行四边形,
所以C1M1=CM.
又因为B1C1=BC,所以△BCM≌△B1C1M1,
所以∠BMC=∠B1M1C1.
【类题通法】
平行线的传递性的应用
1.空间两条直线平行的证明
一是定义法:即证明两条直线在同一个平面内且两直线没有公共点;
二是利用平面图形的有关平行的性质,如三角形中位线,梯形,平行四边形等关于平行的性质;
三是利用平行线的传递性,找到一条直线,使所证的直线都与这条直线平行.
2.求证角相等
一是用等角定理;二是用平面几何知识.
【定向训练】
如图所示,已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点:
(1)求证:E,F,G,H四点共面;
(2)若四边形EFGH是矩形,求证:AC⊥BD.
【解析】(1)在△ABD中,
因为E,H分别是AB,AD的中点,所以EH∥BD.
同理FG∥BD,则EH∥FG.
故E,F,G,H四点共面;
(2)由(1)知EH∥BD,同理AC∥GH.
又因为四边形EFGH是矩形,
所以EH⊥GH.故AC⊥BD.
【补偿训练】
已知棱长为a的正方体ABCD-A1B1C1D1中,M,N分别是棱CD,AD的中点.求证:
(1)四边形MNA1C1是梯形;
(2)∠DNM=∠D1A1C1.
【证明】(1)如图,连接AC,
在△ACD中,因为M,N分别是CD,AD的中点,
所以MN是△ACD的中位线,
所以MN∥AC,MN= AC,
由正方体的性质得AC∥A1C1,AC=A1C1.
所以MN∥A1C1,且MN= A1C1,即MN≠A1C1,
所以四边形MNA1C1是梯形.
(2)由(1)可知MN∥A1C1,又因为ND∥A1D1,
所以∠DNM与∠D1A1C1相等或互补.
而∠DNM与∠D1A1C1均是直角三角形的一个锐角,
所以∠DNM=∠D1A1C1.
探究点二 空间直线位置关系的判定
【典例2】(1)在正方体ABCD????A1B1C1D1中,棱所在直线与直线BA1是异面直线的条数为 ( )
A.4 B.5
C.6 D.7
(2)如图,三棱柱ABC-A1B1C1中,底面三角形A1B1C1是正三角形,E是BC的中点,则下列叙述正确的是 ( )
A.CC1与B1E是异面直线
B.CC1与AE是共面直线
C.AE与B1C1是异面直线
D.AE与BB1是共面直线
【思维导引】(1)根据异面直线的定义判断.
(2)根据异面直线的判定方法判断.
【解析】(1)选C.如图,在正方体ABCD-A1B1C1D1中与BA1所在直线是异面直线的有DC,DA,D1C1,B1C1,DD1,CC1,共6条.
(2)选C.由于CC1与B1E均在平面BCC1B1内,不是异面直线;CC1∩平面ABC=C,
AE?平面ABC,点C不在直线AE上,所以CC1和AE是异面直线,同理BB1与AE是异面直线,AE∩平面BCC1B1=E,B1C1?平面BCC1B1,点E不在直线B1C1上,则AE与B1C1是异面直线.
【类题通法】
判断空间中两条直线位置关系的诀窍
(1)建立空间观念,全面考虑两条直线平行、相交和异面三种位置关系.特别关注异面直线.
(2)重视正方体等常见几何体模型的应用,会举例说明两条直线的位置关系.
【定向训练】
在四棱锥P-ABCD中,各棱所在的直线互相异面的有________对.?
【解析】以底边所在直线为准进行考查,因为四边形ABCD是平面图形,4条边在同一平面内,不可能组成异面直线,而每一边所在直线能与2条侧棱组成2对异面直线,所以共有4×2=8对异面直线.
答案:8
【补偿训练】
某正方体的平面展开图如图所示,则在这个正方体中 ( )
A.NC与DE相交
B.CM与ED平行
C.AF与CN平行
D.AF与CM异面
【解析】选B.根据题意得到正方体如图所示:
对于A,NC与DE是异面直线,故不相交;
对于B,CM与ED平行,由立体图知是正确的;
对于C,AF与CN不同在任何一个平面内,故不正确;
对于D,AF与CM是相交的.
探究点三 空间四边形的认识
【典例3】如图,设E,F,G,H分别是四面体A-BCD的棱AB,BC,CD,DA上的点,
且 ,求证:
(1)当λ=μ时,四边形EFGH是平行四边形;
(2)当λ≠μ时,四边形EFGH是梯形.
【思维导引】空间四边形各边中点连线构成平行四边形是空间四边形的一个重要性质,这样就可以利用平行四边形性质解决相关问题,因而先利用三角形中位线证明有关线段平行.
【证明】(1)因为 =λ,所以EH∥BD,所以 =λ,
同理GF∥BD, =μ,又因为λ=μ,所以EH=GF,
所以EH???? GF,所以四边形EFGH是平行四边形.
(2)由(1)知EH∥GF,又因为λ≠μ,
所以EH≠GF.所以四边形EFGH是梯形.
【类题通法】
空间四边形中的平行关系
因空间图形往往包含平面图形,在解题时容易混淆,所以把相似的概念辨析一下,区分异同,解题时才不出错,如本例中明确给出了“空间四边形ABCD”,不包含平面四边形,说明“A,B,C,D四点必不共面”,不能因直观图中AD与BC看似平行的关系认为它们是平行的.
【定向训练】
已知四边形ABCD是空间四边形,E,H分别是边AB,AD的中点,F,G分别是
边CB,CD上的点,且
求证:FE和GH的交点在直线AC上.
【证明】连接BD,因为E,H分别是边AB,AD的中点,所以EH∥BD.
又因为 ,所以FG∥BD.
因此EH∥FG,且EH≠FG,故四边形EFGH是梯形;
所以EF,HG相交,
设EF∩HG=K.
因为K∈EF,EF?平面ABC,所以K∈平面ABC,
同理K∈平面ACD.
又平面ABC∩平面ACD=AC,
所以K∈AC,故FE和GH的交点在直线AC上.
【课堂小结】
课堂素养达标
1.如图,在长方体ABCD-A1B1C1D1中,与AA1异面的棱是 ( )
A.AB B.BB1 C.DD1 D.B1C1
【解析】选D.AA1∥BB1,AA1∥DD1,AA1∩AB=A,AA1与B1C1是异面直线.
2.一条直线与两条异面直线中的一条平行,则它和另一条的位置关系
是 ( )
A.平行或异面 B.相交或异面
C.异面 D.相交
【解析】选B.假设a与b是异面直线,而c∥a,则c显然与b不平行(否则c∥b,则有a∥b,与a,b是异面直线矛盾),因此c与b可能相交或异面.
3.已知直线a∥直线b,直线b∥直线c,直线c∥直线d,则a与d的位置关系
是 ( )
A.平行 B.相交 C.异面 D.不确定
【解析】选A.因为a∥b,b∥c,所以a∥c.
又c∥d,所以a∥d.
4.两条直线a,b分别和异面直线c,d都相交,则直线a,b的位置关系
是 ( )
A.平行 B.相交
C.异面 D.异面或相交
【解析】选D.已知直线c与d是异面直线,直线a,b分别与直线c,d相交于点A,B,C,D,
根据题意可得,当点D与点B重合时(或当点A与点C重合时),两条直线相交,当点D与点B不重合且点A与点C不重合时,两条直线异面.
11.3.1 平行直线与异面直线
基础预习初探
1.在同一平面内,两条直线有几种位置关系?
2.观察如图正方体ABCD-A1B1C1D1,回答下面的问题:
(1)图中∠C1A1B1和∠CAB有什么关系?
(2)图中A1C1∥AC,则“直线A1C1与直线BC1所成的角”与“直线AC与直线BC1所成的角”是否相等?
继续探究:
1.空间中,没有公共点的两条直线一定平行吗?
提示:不一定,在平面内没有公共点的两条直线平行,在空间没有公共点的两条直线可能平行,也可能异面.
2.如图长方体,观察图中的直线,你能得出哪些位置关系?
提示:(1)平行关系:图中AD与BC,BC与B1C1等所在直线是平行关系.
(2)相交关系:图中AB与BC,A1B与BC等所在直线是相交关系.
(3)异面关系:图中AA1与BC所在直线,它们既不相交也不平行,是异面关系.
【概念生成】
1.平行直线
(1)过直线外一点_____________直线与已知直线平行;
(2)平行直线的传递性:平行于同一条直线的两条直线_________.这一性质
叫做空间平行线的_______.
符号表述: ?b∥c.
(3)等角定理
如果一个角的两边与另一个角的两边分别_________,并且方向_____,那么
这两个角_____.
有且只有一条
互相平行
传递性
对应平行
相同
相等
2.异面直线
(1)画法:如图,为了表示异面直线a,b不共面的特点,作图时,通常用一个或两个平面衬托.
(2)判定:
与一个平面相交于一点的直线与这个平面内___________的直线异面.
不经过交点
3.空间四边形
顺次连接_______的4点所构成的图形,称为空间四边形.其中4个点都是空间四
边形的_____;连接相邻顶点间的线段称为空间四边形的___;连接不相邻顶点间
的线段称为空间四边形的_______.空间四边形用表示顶点的4个字母表示.
不共面
顶点
对角线
边
核心互动探究
探究点一 等角定理的应用
【典例1】如图所示,在正方体ABCD-A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.求证:
(1)四边形BB1M1M为平行四边形;
(2)∠BMC=∠B1M1C1.
【思维导引】(1)欲证四边形BB1M1M是平行四边形,可证其一组对边平行且相等;(2)可结合(1)利用等角定理证明或利用三角形全等证明.
【证明】(1)因为ABCD-A1B1C1D1为正方体.
所以AD=A1D1,且AD∥A1D1,
又M,M1分别为棱AD,A1D1的中点,
所以AM=A1M1且AM∥A1M1,
所以四边形AMM1A1为平行四边形,
所以MM1=AA1且MM1∥AA1.
又AA1=BB1且AA1∥BB1,
所以MM1=BB1且MM1∥BB1,
所以四边形BB1M1M为平行四边形;
(2)方法一:由(1)知四边形BB1M1M为平行四边形,
所以B1M1∥BM.同理可得四边形CC1M1M为平行四边形,所以C1M1∥CM.
因为∠BMC和∠B1M1C1方向相同,
所以∠BMC=∠B1M1C1.
方法二:由(1)知四边形BB1M1M为平行四边形,
所以B1M1=BM.
同理可得四边形CC1M1M为平行四边形,
所以C1M1=CM.
又因为B1C1=BC,所以△BCM≌△B1C1M1,
所以∠BMC=∠B1M1C1.
【类题通法】
平行线的传递性的应用
1.空间两条直线平行的证明
一是定义法:即证明两条直线在同一个平面内且两直线没有公共点;
二是利用平面图形的有关平行的性质,如三角形中位线,梯形,平行四边形等关于平行的性质;
三是利用平行线的传递性,找到一条直线,使所证的直线都与这条直线平行.
2.求证角相等
一是用等角定理;二是用平面几何知识.
【定向训练】
如图所示,已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点:
(1)求证:E,F,G,H四点共面;
(2)若四边形EFGH是矩形,求证:AC⊥BD.
【解析】(1)在△ABD中,
因为E,H分别是AB,AD的中点,所以EH∥BD.
同理FG∥BD,则EH∥FG.
故E,F,G,H四点共面;
(2)由(1)知EH∥BD,同理AC∥GH.
又因为四边形EFGH是矩形,
所以EH⊥GH.故AC⊥BD.
【补偿训练】
已知棱长为a的正方体ABCD-A1B1C1D1中,M,N分别是棱CD,AD的中点.求证:
(1)四边形MNA1C1是梯形;
(2)∠DNM=∠D1A1C1.
【证明】(1)如图,连接AC,
在△ACD中,因为M,N分别是CD,AD的中点,
所以MN是△ACD的中位线,
所以MN∥AC,MN= AC,
由正方体的性质得AC∥A1C1,AC=A1C1.
所以MN∥A1C1,且MN= A1C1,即MN≠A1C1,
所以四边形MNA1C1是梯形.
(2)由(1)可知MN∥A1C1,又因为ND∥A1D1,
所以∠DNM与∠D1A1C1相等或互补.
而∠DNM与∠D1A1C1均是直角三角形的一个锐角,
所以∠DNM=∠D1A1C1.
探究点二 空间直线位置关系的判定
【典例2】(1)在正方体ABCD????A1B1C1D1中,棱所在直线与直线BA1是异面直线的条数为 ( )
A.4 B.5
C.6 D.7
(2)如图,三棱柱ABC-A1B1C1中,底面三角形A1B1C1是正三角形,E是BC的中点,则下列叙述正确的是 ( )
A.CC1与B1E是异面直线
B.CC1与AE是共面直线
C.AE与B1C1是异面直线
D.AE与BB1是共面直线
【思维导引】(1)根据异面直线的定义判断.
(2)根据异面直线的判定方法判断.
【解析】(1)选C.如图,在正方体ABCD-A1B1C1D1中与BA1所在直线是异面直线的有DC,DA,D1C1,B1C1,DD1,CC1,共6条.
(2)选C.由于CC1与B1E均在平面BCC1B1内,不是异面直线;CC1∩平面ABC=C,
AE?平面ABC,点C不在直线AE上,所以CC1和AE是异面直线,同理BB1与AE是异面直线,AE∩平面BCC1B1=E,B1C1?平面BCC1B1,点E不在直线B1C1上,则AE与B1C1是异面直线.
【类题通法】
判断空间中两条直线位置关系的诀窍
(1)建立空间观念,全面考虑两条直线平行、相交和异面三种位置关系.特别关注异面直线.
(2)重视正方体等常见几何体模型的应用,会举例说明两条直线的位置关系.
【定向训练】
在四棱锥P-ABCD中,各棱所在的直线互相异面的有________对.?
【解析】以底边所在直线为准进行考查,因为四边形ABCD是平面图形,4条边在同一平面内,不可能组成异面直线,而每一边所在直线能与2条侧棱组成2对异面直线,所以共有4×2=8对异面直线.
答案:8
【补偿训练】
某正方体的平面展开图如图所示,则在这个正方体中 ( )
A.NC与DE相交
B.CM与ED平行
C.AF与CN平行
D.AF与CM异面
【解析】选B.根据题意得到正方体如图所示:
对于A,NC与DE是异面直线,故不相交;
对于B,CM与ED平行,由立体图知是正确的;
对于C,AF与CN不同在任何一个平面内,故不正确;
对于D,AF与CM是相交的.
探究点三 空间四边形的认识
【典例3】如图,设E,F,G,H分别是四面体A-BCD的棱AB,BC,CD,DA上的点,
且 ,求证:
(1)当λ=μ时,四边形EFGH是平行四边形;
(2)当λ≠μ时,四边形EFGH是梯形.
【思维导引】空间四边形各边中点连线构成平行四边形是空间四边形的一个重要性质,这样就可以利用平行四边形性质解决相关问题,因而先利用三角形中位线证明有关线段平行.
【证明】(1)因为 =λ,所以EH∥BD,所以 =λ,
同理GF∥BD, =μ,又因为λ=μ,所以EH=GF,
所以EH???? GF,所以四边形EFGH是平行四边形.
(2)由(1)知EH∥GF,又因为λ≠μ,
所以EH≠GF.所以四边形EFGH是梯形.
【类题通法】
空间四边形中的平行关系
因空间图形往往包含平面图形,在解题时容易混淆,所以把相似的概念辨析一下,区分异同,解题时才不出错,如本例中明确给出了“空间四边形ABCD”,不包含平面四边形,说明“A,B,C,D四点必不共面”,不能因直观图中AD与BC看似平行的关系认为它们是平行的.
【定向训练】
已知四边形ABCD是空间四边形,E,H分别是边AB,AD的中点,F,G分别是
边CB,CD上的点,且
求证:FE和GH的交点在直线AC上.
【证明】连接BD,因为E,H分别是边AB,AD的中点,所以EH∥BD.
又因为 ,所以FG∥BD.
因此EH∥FG,且EH≠FG,故四边形EFGH是梯形;
所以EF,HG相交,
设EF∩HG=K.
因为K∈EF,EF?平面ABC,所以K∈平面ABC,
同理K∈平面ACD.
又平面ABC∩平面ACD=AC,
所以K∈AC,故FE和GH的交点在直线AC上.
【课堂小结】
课堂素养达标
1.如图,在长方体ABCD-A1B1C1D1中,与AA1异面的棱是 ( )
A.AB B.BB1 C.DD1 D.B1C1
【解析】选D.AA1∥BB1,AA1∥DD1,AA1∩AB=A,AA1与B1C1是异面直线.
2.一条直线与两条异面直线中的一条平行,则它和另一条的位置关系
是 ( )
A.平行或异面 B.相交或异面
C.异面 D.相交
【解析】选B.假设a与b是异面直线,而c∥a,则c显然与b不平行(否则c∥b,则有a∥b,与a,b是异面直线矛盾),因此c与b可能相交或异面.
3.已知直线a∥直线b,直线b∥直线c,直线c∥直线d,则a与d的位置关系
是 ( )
A.平行 B.相交 C.异面 D.不确定
【解析】选A.因为a∥b,b∥c,所以a∥c.
又c∥d,所以a∥d.
4.两条直线a,b分别和异面直线c,d都相交,则直线a,b的位置关系
是 ( )
A.平行 B.相交
C.异面 D.异面或相交
【解析】选D.已知直线c与d是异面直线,直线a,b分别与直线c,d相交于点A,B,C,D,
根据题意可得,当点D与点B重合时(或当点A与点C重合时),两条直线相交,当点D与点B不重合且点A与点C不重合时,两条直线异面.
