11.1.2构成空间几何体的基本元素 课件 2020-2021学年高一下学期数学人教B版(2019)必修第四册(35张PPT)
文档属性
| 名称 | 11.1.2构成空间几何体的基本元素 课件 2020-2021学年高一下学期数学人教B版(2019)必修第四册(35张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 754.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 09:59:30 | ||
图片预览






文档简介
11.1.2 构成空间几何体的基本元素
新课程标准
素养风向标
1.通过对长方体的认识,了解构成几何体的基本元素和它们之间的关系.
2.掌握点、线、面之间的位置关系.
3.理解异面直线的定义,会画两条异面直线.
1.了解空间中点、线、面、体之间的关系.(直观想象)
2.了解轨迹和图形的关系.(数学抽象)
3.初步了解空间中直线与直线、直线与平面、平面与平面间的位置关系.(逻辑推理)
4.会用符号语言和图形语言表示直线和平面、平面和平面之间的位置关系.(直观想象)
基础预习初探
1.在我们周围存在着各种各样的物体,它们都占据着空间的一部分,如果我们只考虑一个物体占空间部分的形状和大小,而不考虑其他因素,则这个空间部分叫做一个几何体,那么构成几何体的基本元素有哪些?这些元素之间有怎样的关系?
2.空间几何体在生活中很常见,你知道这些几何体是如何画出来的吗?
继续探究:(1)直线平行移动一定形成平面吗?
提示:不一定,还可能形成曲面.
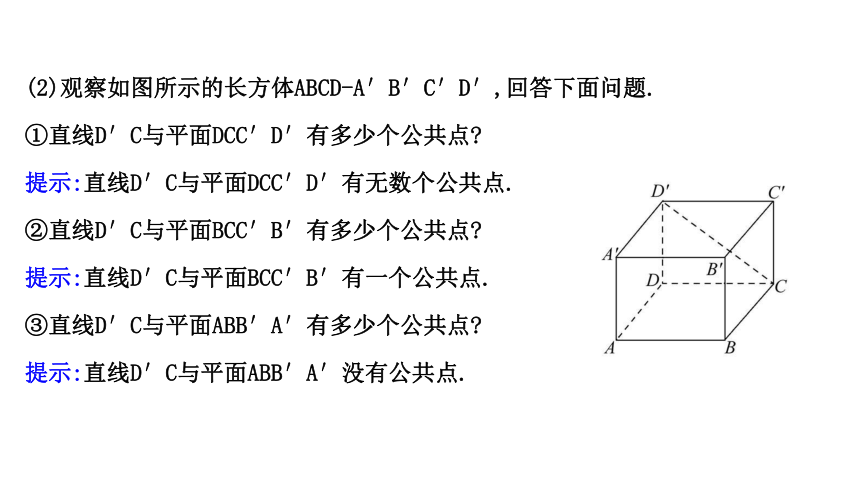
(2)观察如图所示的长方体ABCD-A′B′C′D′,回答下面问题.
①直线D′C与平面DCC′D′有多少个公共点?
提示:直线D′C与平面DCC′D′有无数个公共点.
②直线D′C与平面BCC′B′有多少个公共点?
提示:直线D′C与平面BCC′B′有一个公共点.
③直线D′C与平面ABB′A′有多少个公共点?
提示:直线D′C与平面ABB′A′没有公共点.
【概念生成】
1.构成空间几何体的基本元素
___、___、___是构成空间几何体的基本元素.
2.点、直线、平面位置关系的符号表示
一般用集合符号“∈”“∩”“?”等描述点、直线、平面之间的位置关系.
若A是点,l,m是直线,α,β是平面,则有:
点
线
面
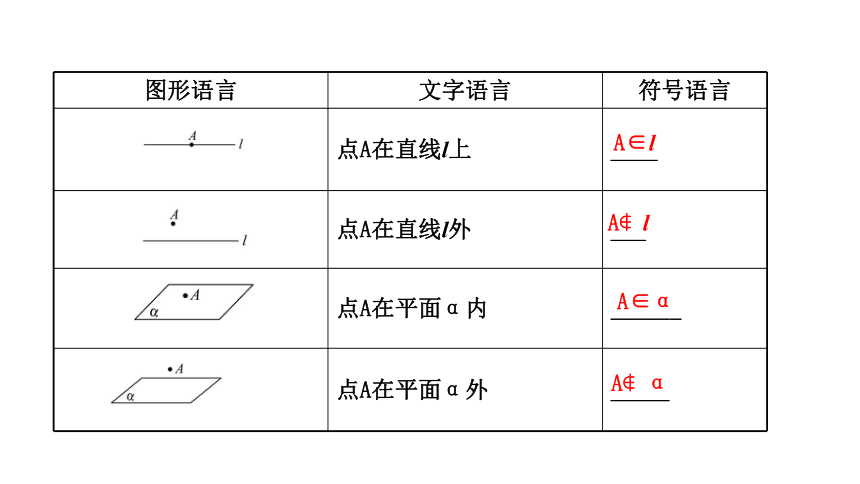
图形语言
文字语言
符号语言
点A在直线l上
____
点A在直线l外
___
点A在平面α内
______
点A在平面α外
_____
A∈l
A?l
A∈α
A?α
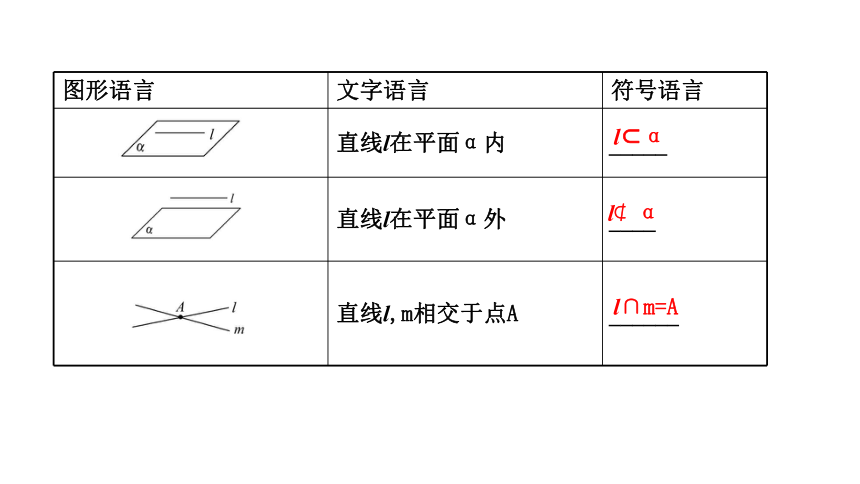
图形语言
文字语言
符号语言
直线l在平面α内
_____
直线l在平面α外
____
直线l,m相交于点A
______
l?α
l?α
l∩m=A
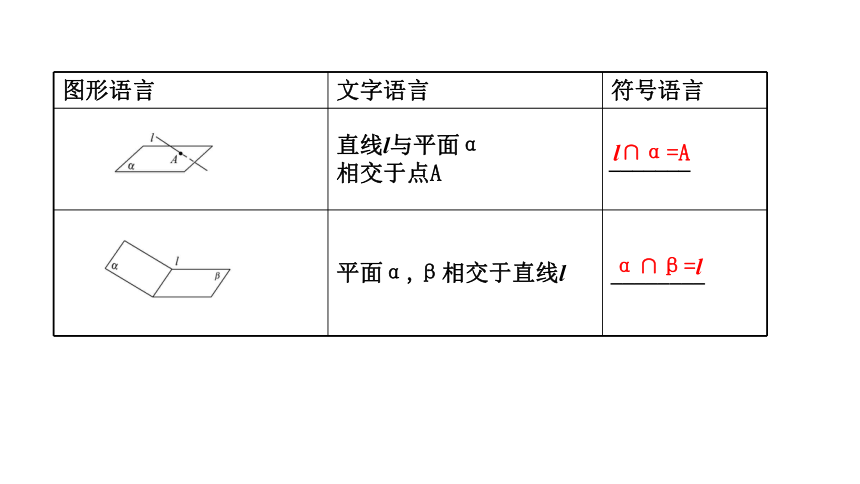
图形语言
文字语言
符号语言
直线l与平面α
相交于点A
_______
平面α,β相交于直线l
________
l∩α=A
α∩β=l
3.空间中直线与直线的位置关系
(1)异面直线:空间中的两条直线可以既不平行,也不_____,此时称这两条直线
异面.
(2)空间中直线与直线有_____、_____与_____三种位置关系.
相交
相交
平行
异面
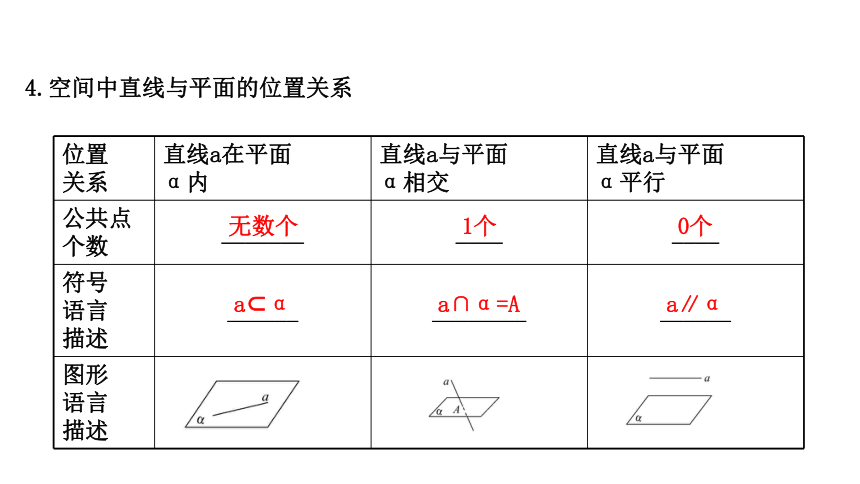
4.空间中直线与平面的位置关系
位置
关系
直线a在平面
α内
直线a与平面
α相交
直线a与平面
α平行
公共点
个数
_______
____
____
符号
语言
描述
______
________
______
图形
语言
描述
无数个
1个
0个
a?α
a∩α=A
a∥α
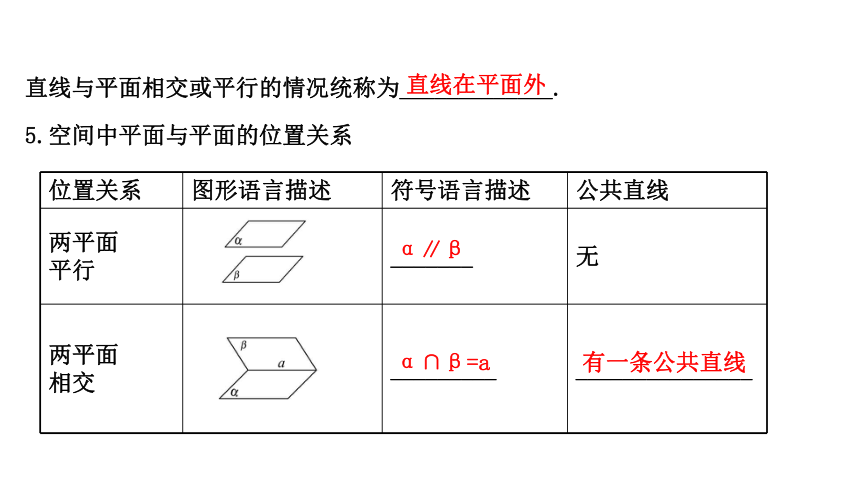
直线与平面相交或平行的情况统称为_____________.
5.空间中平面与平面的位置关系
位置关系
图形语言描述
符号语言描述
公共直线
两平面
平行
_______
无
两平面
相交
_________
_______________
直线在平面外
α∥β
α∩β=a
有一条公共直线
6.直线与平面垂直的定义
一般地,如果直线l与平面α相交于一点A,且对平面α内_________过点A的直
线m,都有l⊥m,则称直线l与平面α垂直(或l是平面α的一条垂线,α是直线l的
一个垂面),记作l⊥α,其中点A称为垂足.
7.空间中的距离
(1)点到平面的距离
由长方体可以看出,给定空间中一个平面α及一个点A,过A可以作而且只可以
作平面α的一条_____.如果记垂足为B,则称B为A在平面α内的射影(也称为投
影),线段___为平面α的垂线段,AB的长为点A到这个平面的距离.
任意一条
垂线
AB
(2)直线到平面的距离
当直线与平面平行时,直线上任意一点到平面的距离称为这条直线到这个平面
的距离.
(3)两平行平面间的距离
当平面与平面_____时,一个平面上任意一点到另一个平面的距离称为这两个
平行平面之间的距离.
平行
核心互动探究
探究点一 几何体的基本元素
【典例1】试指出下图中各几何体的基本元素.
【思维导引】联想实物从点、线、面三个角度进行观察.
【解析】(1)中几何体有6个顶点,12条棱和8个面.
(2)中几何体有12个顶点,18条棱和8个面.
(3)中几何体有6个顶点,10条棱和6个面.
(4)中几何体有2条曲线,3个面(2个平面和1个曲面).
【类题通法】
构成空间几何体的基本元素的特性
点是最基本的元素,只有位置,没有大小;直线没有粗细,向两方无限延伸;平面没有厚度,向周围无限延展.要熟记这三种基本元素的特点.在现实生活中要多观察几何体,以便加深对构成空间几何体的基本元素的认识.
【定向训练】
如图所示,该几何体是某同学课桌的大致轮廓,请你从这个几何体里面寻找一些点、线、面,并将它们列举出来.
【解析】面可以列举如下:
平面A1A2B2B1,平面A1A2D2D1,平面C1C2D2D1,
平面B1B2C2C1,平面A1B1C1D1,平面A2B2C2D2.
线可以列举如下:直线AA1,直线BB1,直线CC1,直线DD1,直线A2B2,直线C2D2等;
点可以列举如下:点A,点A1,点B,点B1,点C,点C1,点D,点D1,点A2,点B2,点C2,点D2.
它们共同组成了课桌这个几何体.
【补偿训练】
指出所给两个几何图形的面、顶点、棱,并指出它们分别由几个面围成,各有多少条棱?多少个顶点?
【解析】(1)中,面SAB、面SBC、面SCD、面SAD、面ABCD,共5个,棱SA、SB、SC、SD、AB、BC、CD、DA,共8条,顶点S、A、B、C、D,共5个.
(2)中,面ABCD、面A1B1C1D1、面ABB1A1、面BCC1B1、面CDD1C1、面DAA1D1,共6个,棱AB、BC、CD、DA、A1B1、B1C1、C1D1、D1A1、A1A、B1B、C1C、D1D,共12条,顶点A1、B1、C1、D1、A、B、C、D,共8个.
探究点二 三种语言的转化
【典例2】(1)用符号语言表示下面的语句.
平面ABD与平面BDC交于BD,平面ABC与平面ADC交于AC;
(2)将下面用符号语言表示的关系用文字语言予以叙述α∩β=l,A∈l,AB?α,AC?β.
【思维导引】根据点、线、面位置关系的符号表示判断.
【解析】(1)用符号语言表示:平面ABD∩平面BDC=BD,平面ABC∩平面ADC=AC.
(2)用文字语言叙述为:点A在平面α与平面β的交线l上,直线AB,AC分别在平面α、β内.
【类题通法】
三种语言的转换方法
(1)用文字语言、符号语言表示一个图形时,首先仔细观察图形有几个平面、几条直线且相互之间的位置关系如何,试着用文字语言表示,再用符号语言表示.
(2)根据符号语言或文字语言画相应的图形时,要注意实线和虚线的区别.
(3)转化时要注意符号的使用,“∈”或“?”反映的是点与线,点与面的关系,而“?”或“?”反映的是直线与平面的关系.
【定向训练】
平面α与平面β平行,且a?α,有下列四种说法:
①a与β内的所有直线都平行;②a与β内无数条直线平行;③a与β内的任意一条直线都不垂直;④a与β无公共点.其中正确说法的个数是 ( )
A.1 B.2 C.3 D.4
【解析】选B.如图,在长方体中,平面ABCD∥平面A′B′C′D′,A′D′?平面A′B′C′D′,AB?平面ABCD,A′D′与AB不平行,且A′D′与AB垂直,所以①③错误.
探究点三 直线与平面、平面与平面的位置关系
【典例3】如图所示,在长方体ABCD-A′B′C′D′中,如果把它的12条棱延伸为直线,6个面延展为平面,那么在这12条直线与6个平面中:
(1)与直线B′C′平行的平面有哪几个?
(2)与平面BC′平行的平面有哪几个?
(3)与平面BC′垂直的平面有哪几个?
(4)与棱AB异面的棱有哪些?
(5)与平面A′B′BA平行的平面有哪些?
【思维导引】细心观察图形,找出与直线B′C′和平面BC′平行、垂直的平面,与棱AB异面的棱,与平面A′B′BA平行的平面.
【解析】(1)与直线B′C′平行的平面有:平面AD′,平面AC.
(2)与平面BC′平行的平面有:平面AD′.
(3)与平面BC′垂直的平面有:平面AB′,平面A′C′,
平面CD′,平面AC.
(4)如题图,长方体ABCD-A′B′C′D′中,与AB异面的棱有A′D′,B′C′,CC′,DD′四条.
(5)与平面A′B′BA平行的平面有CDD′C′一个.
【类题通法】
判断线面位置关系的方法
1.解决此类问题的关键在于识图,根据图形识别直线与平面平行、垂直,平面与平面平行、垂直.
2.长方体和正方体是立体几何中的重要几何体,对其认识有助于进一步认识立体几何中的点、线、面的基本关系.
【定向训练】
直线a在平面γ外,则 ( )
A.a∥γ B.a与γ至少有一个公共点
C.a∩γ=A D.a与γ至多有一个公共点
【解析】选D.直线a在平面γ外,包括两种情况,一种是平行,另一种是相交.
【课堂小结】
课堂素养达标
1.下列关于长方体的叙述不正确的是 ( )
A.将一个矩形沿竖直方向平移一段距离可形成一个长方体
B.长方体中相对的面都相互平行
C.长方体中某一底面上的高的长度就是两平行底面间的距离
D.两底面之间的棱互相平行且等长
【解析】选A.将一个矩形沿不与面垂直的方向平移时不能形成长方体.
2.如图所示,下列符号表示错误的是 ( )
A.l∈α B.P?l C.l?α D.P∈α
【解析】选A.观察图知:P?l,P∈α,l?α.A错.
3.看图填空:
(1)平面AB1∩平面A1C1=________;?
(2)平面A1C1CA∩平面AC=________.?
答案:(1)A1B1 (2)AC
新课程标准
素养风向标
1.通过对长方体的认识,了解构成几何体的基本元素和它们之间的关系.
2.掌握点、线、面之间的位置关系.
3.理解异面直线的定义,会画两条异面直线.
1.了解空间中点、线、面、体之间的关系.(直观想象)
2.了解轨迹和图形的关系.(数学抽象)
3.初步了解空间中直线与直线、直线与平面、平面与平面间的位置关系.(逻辑推理)
4.会用符号语言和图形语言表示直线和平面、平面和平面之间的位置关系.(直观想象)
基础预习初探
1.在我们周围存在着各种各样的物体,它们都占据着空间的一部分,如果我们只考虑一个物体占空间部分的形状和大小,而不考虑其他因素,则这个空间部分叫做一个几何体,那么构成几何体的基本元素有哪些?这些元素之间有怎样的关系?
2.空间几何体在生活中很常见,你知道这些几何体是如何画出来的吗?
继续探究:(1)直线平行移动一定形成平面吗?
提示:不一定,还可能形成曲面.
(2)观察如图所示的长方体ABCD-A′B′C′D′,回答下面问题.
①直线D′C与平面DCC′D′有多少个公共点?
提示:直线D′C与平面DCC′D′有无数个公共点.
②直线D′C与平面BCC′B′有多少个公共点?
提示:直线D′C与平面BCC′B′有一个公共点.
③直线D′C与平面ABB′A′有多少个公共点?
提示:直线D′C与平面ABB′A′没有公共点.
【概念生成】
1.构成空间几何体的基本元素
___、___、___是构成空间几何体的基本元素.
2.点、直线、平面位置关系的符号表示
一般用集合符号“∈”“∩”“?”等描述点、直线、平面之间的位置关系.
若A是点,l,m是直线,α,β是平面,则有:
点
线
面
图形语言
文字语言
符号语言
点A在直线l上
____
点A在直线l外
___
点A在平面α内
______
点A在平面α外
_____
A∈l
A?l
A∈α
A?α
图形语言
文字语言
符号语言
直线l在平面α内
_____
直线l在平面α外
____
直线l,m相交于点A
______
l?α
l?α
l∩m=A
图形语言
文字语言
符号语言
直线l与平面α
相交于点A
_______
平面α,β相交于直线l
________
l∩α=A
α∩β=l
3.空间中直线与直线的位置关系
(1)异面直线:空间中的两条直线可以既不平行,也不_____,此时称这两条直线
异面.
(2)空间中直线与直线有_____、_____与_____三种位置关系.
相交
相交
平行
异面
4.空间中直线与平面的位置关系
位置
关系
直线a在平面
α内
直线a与平面
α相交
直线a与平面
α平行
公共点
个数
_______
____
____
符号
语言
描述
______
________
______
图形
语言
描述
无数个
1个
0个
a?α
a∩α=A
a∥α
直线与平面相交或平行的情况统称为_____________.
5.空间中平面与平面的位置关系
位置关系
图形语言描述
符号语言描述
公共直线
两平面
平行
_______
无
两平面
相交
_________
_______________
直线在平面外
α∥β
α∩β=a
有一条公共直线
6.直线与平面垂直的定义
一般地,如果直线l与平面α相交于一点A,且对平面α内_________过点A的直
线m,都有l⊥m,则称直线l与平面α垂直(或l是平面α的一条垂线,α是直线l的
一个垂面),记作l⊥α,其中点A称为垂足.
7.空间中的距离
(1)点到平面的距离
由长方体可以看出,给定空间中一个平面α及一个点A,过A可以作而且只可以
作平面α的一条_____.如果记垂足为B,则称B为A在平面α内的射影(也称为投
影),线段___为平面α的垂线段,AB的长为点A到这个平面的距离.
任意一条
垂线
AB
(2)直线到平面的距离
当直线与平面平行时,直线上任意一点到平面的距离称为这条直线到这个平面
的距离.
(3)两平行平面间的距离
当平面与平面_____时,一个平面上任意一点到另一个平面的距离称为这两个
平行平面之间的距离.
平行
核心互动探究
探究点一 几何体的基本元素
【典例1】试指出下图中各几何体的基本元素.
【思维导引】联想实物从点、线、面三个角度进行观察.
【解析】(1)中几何体有6个顶点,12条棱和8个面.
(2)中几何体有12个顶点,18条棱和8个面.
(3)中几何体有6个顶点,10条棱和6个面.
(4)中几何体有2条曲线,3个面(2个平面和1个曲面).
【类题通法】
构成空间几何体的基本元素的特性
点是最基本的元素,只有位置,没有大小;直线没有粗细,向两方无限延伸;平面没有厚度,向周围无限延展.要熟记这三种基本元素的特点.在现实生活中要多观察几何体,以便加深对构成空间几何体的基本元素的认识.
【定向训练】
如图所示,该几何体是某同学课桌的大致轮廓,请你从这个几何体里面寻找一些点、线、面,并将它们列举出来.
【解析】面可以列举如下:
平面A1A2B2B1,平面A1A2D2D1,平面C1C2D2D1,
平面B1B2C2C1,平面A1B1C1D1,平面A2B2C2D2.
线可以列举如下:直线AA1,直线BB1,直线CC1,直线DD1,直线A2B2,直线C2D2等;
点可以列举如下:点A,点A1,点B,点B1,点C,点C1,点D,点D1,点A2,点B2,点C2,点D2.
它们共同组成了课桌这个几何体.
【补偿训练】
指出所给两个几何图形的面、顶点、棱,并指出它们分别由几个面围成,各有多少条棱?多少个顶点?
【解析】(1)中,面SAB、面SBC、面SCD、面SAD、面ABCD,共5个,棱SA、SB、SC、SD、AB、BC、CD、DA,共8条,顶点S、A、B、C、D,共5个.
(2)中,面ABCD、面A1B1C1D1、面ABB1A1、面BCC1B1、面CDD1C1、面DAA1D1,共6个,棱AB、BC、CD、DA、A1B1、B1C1、C1D1、D1A1、A1A、B1B、C1C、D1D,共12条,顶点A1、B1、C1、D1、A、B、C、D,共8个.
探究点二 三种语言的转化
【典例2】(1)用符号语言表示下面的语句.
平面ABD与平面BDC交于BD,平面ABC与平面ADC交于AC;
(2)将下面用符号语言表示的关系用文字语言予以叙述α∩β=l,A∈l,AB?α,AC?β.
【思维导引】根据点、线、面位置关系的符号表示判断.
【解析】(1)用符号语言表示:平面ABD∩平面BDC=BD,平面ABC∩平面ADC=AC.
(2)用文字语言叙述为:点A在平面α与平面β的交线l上,直线AB,AC分别在平面α、β内.
【类题通法】
三种语言的转换方法
(1)用文字语言、符号语言表示一个图形时,首先仔细观察图形有几个平面、几条直线且相互之间的位置关系如何,试着用文字语言表示,再用符号语言表示.
(2)根据符号语言或文字语言画相应的图形时,要注意实线和虚线的区别.
(3)转化时要注意符号的使用,“∈”或“?”反映的是点与线,点与面的关系,而“?”或“?”反映的是直线与平面的关系.
【定向训练】
平面α与平面β平行,且a?α,有下列四种说法:
①a与β内的所有直线都平行;②a与β内无数条直线平行;③a与β内的任意一条直线都不垂直;④a与β无公共点.其中正确说法的个数是 ( )
A.1 B.2 C.3 D.4
【解析】选B.如图,在长方体中,平面ABCD∥平面A′B′C′D′,A′D′?平面A′B′C′D′,AB?平面ABCD,A′D′与AB不平行,且A′D′与AB垂直,所以①③错误.
探究点三 直线与平面、平面与平面的位置关系
【典例3】如图所示,在长方体ABCD-A′B′C′D′中,如果把它的12条棱延伸为直线,6个面延展为平面,那么在这12条直线与6个平面中:
(1)与直线B′C′平行的平面有哪几个?
(2)与平面BC′平行的平面有哪几个?
(3)与平面BC′垂直的平面有哪几个?
(4)与棱AB异面的棱有哪些?
(5)与平面A′B′BA平行的平面有哪些?
【思维导引】细心观察图形,找出与直线B′C′和平面BC′平行、垂直的平面,与棱AB异面的棱,与平面A′B′BA平行的平面.
【解析】(1)与直线B′C′平行的平面有:平面AD′,平面AC.
(2)与平面BC′平行的平面有:平面AD′.
(3)与平面BC′垂直的平面有:平面AB′,平面A′C′,
平面CD′,平面AC.
(4)如题图,长方体ABCD-A′B′C′D′中,与AB异面的棱有A′D′,B′C′,CC′,DD′四条.
(5)与平面A′B′BA平行的平面有CDD′C′一个.
【类题通法】
判断线面位置关系的方法
1.解决此类问题的关键在于识图,根据图形识别直线与平面平行、垂直,平面与平面平行、垂直.
2.长方体和正方体是立体几何中的重要几何体,对其认识有助于进一步认识立体几何中的点、线、面的基本关系.
【定向训练】
直线a在平面γ外,则 ( )
A.a∥γ B.a与γ至少有一个公共点
C.a∩γ=A D.a与γ至多有一个公共点
【解析】选D.直线a在平面γ外,包括两种情况,一种是平行,另一种是相交.
【课堂小结】
课堂素养达标
1.下列关于长方体的叙述不正确的是 ( )
A.将一个矩形沿竖直方向平移一段距离可形成一个长方体
B.长方体中相对的面都相互平行
C.长方体中某一底面上的高的长度就是两平行底面间的距离
D.两底面之间的棱互相平行且等长
【解析】选A.将一个矩形沿不与面垂直的方向平移时不能形成长方体.
2.如图所示,下列符号表示错误的是 ( )
A.l∈α B.P?l C.l?α D.P∈α
【解析】选A.观察图知:P?l,P∈α,l?α.A错.
3.看图填空:
(1)平面AB1∩平面A1C1=________;?
(2)平面A1C1CA∩平面AC=________.?
答案:(1)A1B1 (2)AC
