9.1.2余弦定理 课件 2020-2021学年高一下学期数学人教B版(2019)必修第四册(40张PPT)
文档属性
| 名称 | 9.1.2余弦定理 课件 2020-2021学年高一下学期数学人教B版(2019)必修第四册(40张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 729.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 00:00:00 | ||
图片预览









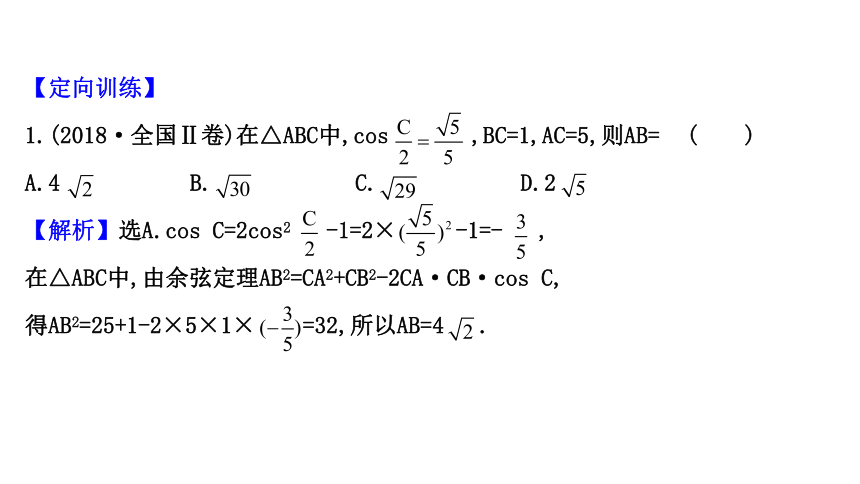
文档简介
9.1.2 余 弦 定 理
基础预习初探
1.回顾勾股定理及其逆定理:
(1)在Rt△ABC中,内角A,B,C的对边分别为a,b,c,如果C=90°,那么a,b,c的关系是________.?
(2)在△ABC中,内角A,B,C的对边分别为a,b,c,如果c2=a2+b2,那么角C的度数为________.?
提示:(1)c2=a2+b2 (2)90°
2.已知△ABC中,内角A,B,C的对边分别为a,b,c,如果a=3,b=4,C=60°,如何计算c的值?
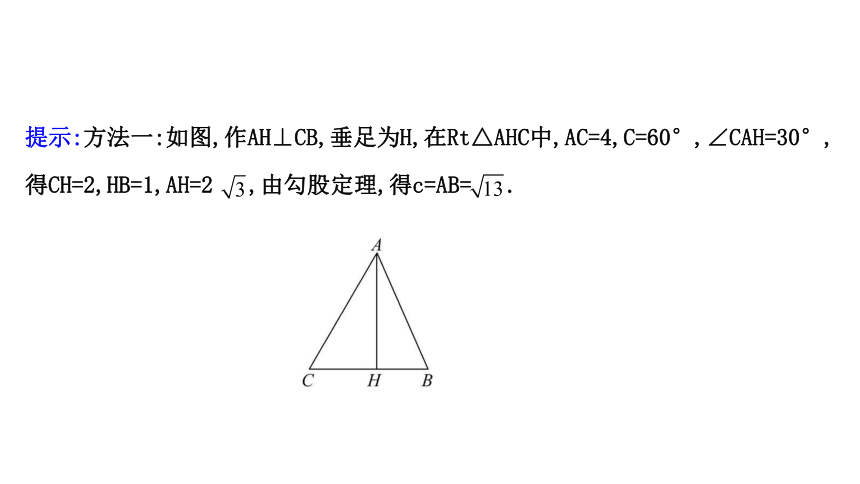
提示:方法一:如图,作AH⊥CB,垂足为H,在Rt△AHC中,AC=4,C=60°,∠CAH=30°,
得CH=2,HB=1,AH=2 ,由勾股定理,得c=AB= .
方法二:在△ABC中,
所以 ,得
= cos 60°
=9+16-2×3×4× =13,所以c= .
方法三:在△ABC中,a=3,b=4,C=60°,由余弦定理,得c2=a2+b2-2abcos C
=9+16-2×3×4× =13,所以c= .
【概念生成】
1.余弦定理
三角形任何一边的平方等于其他两边的_________减去这两边与它们夹角
的余弦的积的____.即
a2=b2+c2-2bccosA;
b2=a2+c2-2accosB;
c2=a2+b2-2abcosC.
平方的和
2倍
2.变形公式
由余弦定理,可以得到如下推论(变形公式):
cos A= ;
cos B= ;
cos C= .
核心互动探究
探究点一 利用余弦定理计算边长
【典例1】1.在△ABC中,若a=2,b= ,C= ,则c= ( )
A.1 B.2 C.3 D.
2.已知△ABC的三个内角A,B,C满足A+C=2B,且AB=1,BC=4,则边BC上的中线AD的长为________,∠ADB=________.?
【思维导引】1.利用余弦定理计算.
2.利用三角形内角和定理以及余弦定理计算.
【解析】1.选D.由余弦定理,得c2=a2+b2-2abcos C=4+3-2×2× cos =13,
所以c= .
2.由△ABC的三个内角A,B,C满足A+C=2B,
且A+B+C=π,可得B= .
AB=1,BC=4,则BD=2,由余弦定理,
得AD=
在△ABD中,因为AB2+AD2 =BD2,
所以∠BAD= ,∠ADB= .
答案:
【类题通法】
利用余弦定理计算的注意事项
1.如果已知三角形的两边和夹角(即SAS)解三角形,那么通常运用余弦定理计算.
2.注意三角形内角和定理(即A+B+C=π)在解三角形中的应用.
【定向训练】
1.(2018·全国Ⅱ卷)在△ABC中,cos ,BC=1,AC=5,则AB= ( )
A.4 B. C. D.2
【解析】选A.cos C=2cos2 -1=2× -1=- ,
在△ABC中,由余弦定理AB2=CA2+CB2-2CA·CB·cos C,
得AB2=25+1-2×5×1× =32,所以AB=4 .
2.在△ABC中,BC=a,AC=b,且a,b是方程x2-2 x+2=0的两根,2cos(A+B)=1.
(1)求角C的度数.
(2)求AB的长.
【解题指南】(1)根据诱导公式可求角C的度数.
(2)用余弦定理可求得AB的长.
【解析】(1)由2cos(A+B)=1,得cos C=cos[π-(A+B)]=-cos(A+B)=- .
且0°(2)因为a,b是方程x2-2 x+2=0的两根,所以a+b=2 ,ab=2,所以
AB2=a2+b2-2abcos120°=(a+b)2-ab=10,得AB= .
探究点二 利用余弦定理计算角
【典例2】1.如果等腰三角形的周长是底边长的5倍,那么它的顶角的余弦值
为 ( )
2.(2019·全国Ⅰ卷)△ABC的内角A,B,C的对边分别为a,b,c,设(sin B-
sin C)2=sin2A-sin Bsin C.
(1)求A.
(2)若 a+b=2c,求sin C.
【思维导引】1.设等腰三角形的底边和腰,利用余弦定理计算.
2.(1)利用正弦定理得到b2+c2-a2=bc,利用余弦定理求cosA再计算A.
(2)利用正弦定理将三边的等式转化为三角函数关系式,利用整体角代换法
及和差角的正弦公式计算sin C=
【解析】1.选D.设等腰三角形ABC的底边长为a,腰为b,则周长为a+2b,
依题意得a+2b=5a,所以b=2a,那么等腰三角形的顶角A的余弦值为
cos A=
2.(1)由(sin B-sin C)2=sin2A-sin Bsin C
得sin2B+sin2C-sin2A=sin Bsin C,
故由正弦定理得b2+c2-a2=bc.
由余弦定理得cos A=
因为0°(2)由(1)知B=120°-C,由 a+b=2c及正弦定理得 sin A+sin(120°-C)
=2sin C,即 cos C+ sin C=2sin C,
可得 sin C-cos C= ,即
所以cos(C+60°)=- .
由于0°故sin C=sin(C+60°-60°)
=sin(C+60°)cos60°-cos(C+60°)sin 60°=
【类题通法】
由余弦定理求角的方法技巧
1.如果已知三角形的三边(即SSS)解三角形,那么通常运用余弦定理的变形
公式计算.
2.由余弦定理的变形公式cos C= ,容易得到下列常用的结论:
C=90°?c2=a2+b2,C<90°?c290°?c2>a2+b2.
提醒:若C是三角形的最大的角,则C≥60°,若C是三角形的最小的角,
则C≤60°.
【定向训练】
1.已知三角形的三边满足条件 =1,则A= ( )
A.30° B.45° C.60° D.120°
【解析】选C.由题得a2-b2-c2+2bc=bc,所以b2+c2-a2=bc,所以2bccos A=bc,
所以cos A= ,因为02.(2020·全国Ⅱ卷)△ABC中,sin2A-sin2B-sin2C=sin Bsin C.
(1)求A;
(2)若BC=3,求△ABC周长的最大值.
【解析】(1)因为sin2A-sin2B-sin2C=sin Bsin C,
所以由正弦定理得:BC2-AC2-AB2=AC·AB,所以cos A=
因为A∈(0,π),所以A=
(2)由(1)知A= ,又BC=3,所以由余弦定理得:
BC2=AC2+AB2-2AC·ABcos A=AC2+AB2+AC·AB=9,
即(AC+AB)2-AC·AB=9.
因为AC·AB≤ (当且仅当AC=AB时取等号),
所以9=(AC+AB)2-AC·AB≥(AC+AB)2-
解得:AC+AB≤2 (当且仅当AC=AB时取等号),所以△ABC的周长=AC+AB+BC≤3+2 ,所以△ABC周长的最大值为3+2 .
【补偿训练】
在△ABC中,已知AB=2,AC=3,A=60°.
(1)求BC的长.
(2)求sin 2C的值.
【解析】(1)在△ABC中,由余弦定理可知,
BC2 = AC2 + AB2-2AC·AB·cos A ,
即BC2=32+22-2×3×2×cos 60°,解得BC= .
(2)由正弦定理可知,
即 ,解得sin C= ,由余弦定理可得,
cos C=
所以sin 2C=2sin Ccos C= 2×
探究点三 由余弦定理判断三角形的形状
【典例3】在△ABC中,如果三边长a,b,c满足a3+b3=c3,那么△ABC的形状
为 ( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.以上均有可能
【思维导引】利用a3+b3=c3得到 =1,且c为最大的边,通过不等式的性
质转化为 >1,再利用余弦定理的变形公式确定角C的取值范围判断.
【解析】选A.依题意知c边最大.因为a3+b3=c3,
所以 =1,所以0< <1,0< <1,
所以
所以 >1,
即a2+b2-c2>0,cos C= >0,
所以0【类题通法】
判断三角形形状的方法技巧
判定三角形形状时,一般考虑两个方向进行变形:
(1)一个方向是转化为角,走三角变形之路.通常是运用正弦定理进行边化角.
(2)另一个方向是转化为边,走代数变形之路,通常是正弦定理、余弦定理结合使用.
【定向训练】
1.在△ABC中,a,b,c分别为角A,B,C的对边,a=2bcos C,则△ABC的形状
为 ( )
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰或直角三角形
【解题指南】利用余弦定理的变形公式转化为三边关系判断.也可以用正弦定理,转化为三角形的内角的三角函数关系判断.
【解析】选A.方法一:在△ABC中,a=2bcos C,
由正弦定理得2Rsin A=4Rsin Bcos C,
又sin A=sin(B+C)=sin Bcos C+cos Bsin C,
得sin Bcos C-cos Bsin C=0,
所以sin(B-C)=0,得B-C=0,B=C,所以b=c,
即△ABC为等腰三角形.
方法二:在△ABC中,由余弦定理得cos C=
所以a=2bcos C=2b· ,得a2=a2+b2-c2,
所以b=c,△ABC的形状为等腰三角形.
2.(1)已知在△ABC中, ,试判断三角形的形状.
(2)已知在△ABC中, ,试判断三角形的形状.
【解析】(1)方法一:利用正弦定理将边转化为角.
因为 ,所以bcos A=acos B,又b=2Rsin B,
a=2Rsin A,所以2Rsin Bcos A=2Rsin Acos B,
所以sin Acos B-cos Asin B=0,所以sin(A-B)=0.
因为0所以A-B=0,即A=B,故三角形是等腰三角形.
方法二:利用余弦定理将角化为边.
因为由题意得bcos A=acos B,
所以b·
所以b2+c2-a2=a2+c2-b2,
所以a2=b2,所以a=b.故此三角形是等腰三角形.
(2)方法一:由已知 及正弦定理得
所以sin2A=sin2B.
所以2A=2B或2A+2B=π,
即A=B或A+B= ,
故△ABC为等腰三角形或直角三角形.
方法二:由已知 ,得bcos B=acos A,
所以
所以b2(a2+c2-b2)=a2(b2+c2-a2),
所以(a2-b2)(a2+b2-c2)=0,
所以a=b或a2+b2=c2?C=90°.
故此三角形是等腰三角形或直角三角形.
【课堂小结】
课堂素养达标
1.在△ABC中, 三边长a,b,c的对角分别为A,B,C,已知a=2,b=3,cos C= ,
则c的值为 ( )
A.2 B.3 C. D.
【解析】选B.因为c2=a2+b2-2abcos C=22+32-2×2×3× =9,所以c=3.
2.若a,b,c为△ABC的三边,B=120°,则a2+c2+ac-b2的值 ( )
A.大于0 B.小于0 C.等于0 D.不确定
【解析】选C.cos B=
所以a2+c2-b2=-ac,即a2+c2+ac-b2=-ac+ac=0.
3.已知三角形的三边长度分别为6,3 ,3 ,则三角形的最大内角的度数
为 ( )
A.90° B.120° C.135° D.150°
【解析】选C.因为三角形的三边长度6,3 ,3 中,3 是最大的边,
则三角形的最大内角θ满足cos θ=
所以θ=135°.
4.在△ABC中,A=60°,最大边和最小边是方程x2-9x+8=0的两个正实数根,
则边BC=________.?
【解析】因为A=60°,所以最大边和最小边所夹的角为A,AB,AC为x2-9x+8=0
的两个正实数根,
则AB+AC=9,AB×AC=8,所以BC2=AB2+AC2-2×AC×AB×cos A=
(AB+AC)2-2×AC×AB×(1+cos A)=92-2×8× =57.所以BC= .
答案:
基础预习初探
1.回顾勾股定理及其逆定理:
(1)在Rt△ABC中,内角A,B,C的对边分别为a,b,c,如果C=90°,那么a,b,c的关系是________.?
(2)在△ABC中,内角A,B,C的对边分别为a,b,c,如果c2=a2+b2,那么角C的度数为________.?
提示:(1)c2=a2+b2 (2)90°
2.已知△ABC中,内角A,B,C的对边分别为a,b,c,如果a=3,b=4,C=60°,如何计算c的值?
提示:方法一:如图,作AH⊥CB,垂足为H,在Rt△AHC中,AC=4,C=60°,∠CAH=30°,
得CH=2,HB=1,AH=2 ,由勾股定理,得c=AB= .
方法二:在△ABC中,
所以 ,得
= cos 60°
=9+16-2×3×4× =13,所以c= .
方法三:在△ABC中,a=3,b=4,C=60°,由余弦定理,得c2=a2+b2-2abcos C
=9+16-2×3×4× =13,所以c= .
【概念生成】
1.余弦定理
三角形任何一边的平方等于其他两边的_________减去这两边与它们夹角
的余弦的积的____.即
a2=b2+c2-2bccosA;
b2=a2+c2-2accosB;
c2=a2+b2-2abcosC.
平方的和
2倍
2.变形公式
由余弦定理,可以得到如下推论(变形公式):
cos A= ;
cos B= ;
cos C= .
核心互动探究
探究点一 利用余弦定理计算边长
【典例1】1.在△ABC中,若a=2,b= ,C= ,则c= ( )
A.1 B.2 C.3 D.
2.已知△ABC的三个内角A,B,C满足A+C=2B,且AB=1,BC=4,则边BC上的中线AD的长为________,∠ADB=________.?
【思维导引】1.利用余弦定理计算.
2.利用三角形内角和定理以及余弦定理计算.
【解析】1.选D.由余弦定理,得c2=a2+b2-2abcos C=4+3-2×2× cos =13,
所以c= .
2.由△ABC的三个内角A,B,C满足A+C=2B,
且A+B+C=π,可得B= .
AB=1,BC=4,则BD=2,由余弦定理,
得AD=
在△ABD中,因为AB2+AD2 =BD2,
所以∠BAD= ,∠ADB= .
答案:
【类题通法】
利用余弦定理计算的注意事项
1.如果已知三角形的两边和夹角(即SAS)解三角形,那么通常运用余弦定理计算.
2.注意三角形内角和定理(即A+B+C=π)在解三角形中的应用.
【定向训练】
1.(2018·全国Ⅱ卷)在△ABC中,cos ,BC=1,AC=5,则AB= ( )
A.4 B. C. D.2
【解析】选A.cos C=2cos2 -1=2× -1=- ,
在△ABC中,由余弦定理AB2=CA2+CB2-2CA·CB·cos C,
得AB2=25+1-2×5×1× =32,所以AB=4 .
2.在△ABC中,BC=a,AC=b,且a,b是方程x2-2 x+2=0的两根,2cos(A+B)=1.
(1)求角C的度数.
(2)求AB的长.
【解题指南】(1)根据诱导公式可求角C的度数.
(2)用余弦定理可求得AB的长.
【解析】(1)由2cos(A+B)=1,得cos C=cos[π-(A+B)]=-cos(A+B)=- .
且0°
AB2=a2+b2-2abcos120°=(a+b)2-ab=10,得AB= .
探究点二 利用余弦定理计算角
【典例2】1.如果等腰三角形的周长是底边长的5倍,那么它的顶角的余弦值
为 ( )
2.(2019·全国Ⅰ卷)△ABC的内角A,B,C的对边分别为a,b,c,设(sin B-
sin C)2=sin2A-sin Bsin C.
(1)求A.
(2)若 a+b=2c,求sin C.
【思维导引】1.设等腰三角形的底边和腰,利用余弦定理计算.
2.(1)利用正弦定理得到b2+c2-a2=bc,利用余弦定理求cosA再计算A.
(2)利用正弦定理将三边的等式转化为三角函数关系式,利用整体角代换法
及和差角的正弦公式计算sin C=
【解析】1.选D.设等腰三角形ABC的底边长为a,腰为b,则周长为a+2b,
依题意得a+2b=5a,所以b=2a,那么等腰三角形的顶角A的余弦值为
cos A=
2.(1)由(sin B-sin C)2=sin2A-sin Bsin C
得sin2B+sin2C-sin2A=sin Bsin C,
故由正弦定理得b2+c2-a2=bc.
由余弦定理得cos A=
因为0°
=2sin C,即 cos C+ sin C=2sin C,
可得 sin C-cos C= ,即
所以cos(C+60°)=- .
由于0°
=sin(C+60°)cos60°-cos(C+60°)sin 60°=
【类题通法】
由余弦定理求角的方法技巧
1.如果已知三角形的三边(即SSS)解三角形,那么通常运用余弦定理的变形
公式计算.
2.由余弦定理的变形公式cos C= ,容易得到下列常用的结论:
C=90°?c2=a2+b2,C<90°?c2
提醒:若C是三角形的最大的角,则C≥60°,若C是三角形的最小的角,
则C≤60°.
【定向训练】
1.已知三角形的三边满足条件 =1,则A= ( )
A.30° B.45° C.60° D.120°
【解析】选C.由题得a2-b2-c2+2bc=bc,所以b2+c2-a2=bc,所以2bccos A=bc,
所以cos A= ,因为0
(1)求A;
(2)若BC=3,求△ABC周长的最大值.
【解析】(1)因为sin2A-sin2B-sin2C=sin Bsin C,
所以由正弦定理得:BC2-AC2-AB2=AC·AB,所以cos A=
因为A∈(0,π),所以A=
(2)由(1)知A= ,又BC=3,所以由余弦定理得:
BC2=AC2+AB2-2AC·ABcos A=AC2+AB2+AC·AB=9,
即(AC+AB)2-AC·AB=9.
因为AC·AB≤ (当且仅当AC=AB时取等号),
所以9=(AC+AB)2-AC·AB≥(AC+AB)2-
解得:AC+AB≤2 (当且仅当AC=AB时取等号),所以△ABC的周长=AC+AB+BC≤3+2 ,所以△ABC周长的最大值为3+2 .
【补偿训练】
在△ABC中,已知AB=2,AC=3,A=60°.
(1)求BC的长.
(2)求sin 2C的值.
【解析】(1)在△ABC中,由余弦定理可知,
BC2 = AC2 + AB2-2AC·AB·cos A ,
即BC2=32+22-2×3×2×cos 60°,解得BC= .
(2)由正弦定理可知,
即 ,解得sin C= ,由余弦定理可得,
cos C=
所以sin 2C=2sin Ccos C= 2×
探究点三 由余弦定理判断三角形的形状
【典例3】在△ABC中,如果三边长a,b,c满足a3+b3=c3,那么△ABC的形状
为 ( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.以上均有可能
【思维导引】利用a3+b3=c3得到 =1,且c为最大的边,通过不等式的性
质转化为 >1,再利用余弦定理的变形公式确定角C的取值范围判断.
【解析】选A.依题意知c边最大.因为a3+b3=c3,
所以 =1,所以0< <1,0< <1,
所以
所以 >1,
即a2+b2-c2>0,cos C= >0,
所以0
判断三角形形状的方法技巧
判定三角形形状时,一般考虑两个方向进行变形:
(1)一个方向是转化为角,走三角变形之路.通常是运用正弦定理进行边化角.
(2)另一个方向是转化为边,走代数变形之路,通常是正弦定理、余弦定理结合使用.
【定向训练】
1.在△ABC中,a,b,c分别为角A,B,C的对边,a=2bcos C,则△ABC的形状
为 ( )
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰或直角三角形
【解题指南】利用余弦定理的变形公式转化为三边关系判断.也可以用正弦定理,转化为三角形的内角的三角函数关系判断.
【解析】选A.方法一:在△ABC中,a=2bcos C,
由正弦定理得2Rsin A=4Rsin Bcos C,
又sin A=sin(B+C)=sin Bcos C+cos Bsin C,
得sin Bcos C-cos Bsin C=0,
所以sin(B-C)=0,得B-C=0,B=C,所以b=c,
即△ABC为等腰三角形.
方法二:在△ABC中,由余弦定理得cos C=
所以a=2bcos C=2b· ,得a2=a2+b2-c2,
所以b=c,△ABC的形状为等腰三角形.
2.(1)已知在△ABC中, ,试判断三角形的形状.
(2)已知在△ABC中, ,试判断三角形的形状.
【解析】(1)方法一:利用正弦定理将边转化为角.
因为 ,所以bcos A=acos B,又b=2Rsin B,
a=2Rsin A,所以2Rsin Bcos A=2Rsin Acos B,
所以sin Acos B-cos Asin B=0,所以sin(A-B)=0.
因为0
方法二:利用余弦定理将角化为边.
因为由题意得bcos A=acos B,
所以b·
所以b2+c2-a2=a2+c2-b2,
所以a2=b2,所以a=b.故此三角形是等腰三角形.
(2)方法一:由已知 及正弦定理得
所以sin2A=sin2B.
所以2A=2B或2A+2B=π,
即A=B或A+B= ,
故△ABC为等腰三角形或直角三角形.
方法二:由已知 ,得bcos B=acos A,
所以
所以b2(a2+c2-b2)=a2(b2+c2-a2),
所以(a2-b2)(a2+b2-c2)=0,
所以a=b或a2+b2=c2?C=90°.
故此三角形是等腰三角形或直角三角形.
【课堂小结】
课堂素养达标
1.在△ABC中, 三边长a,b,c的对角分别为A,B,C,已知a=2,b=3,cos C= ,
则c的值为 ( )
A.2 B.3 C. D.
【解析】选B.因为c2=a2+b2-2abcos C=22+32-2×2×3× =9,所以c=3.
2.若a,b,c为△ABC的三边,B=120°,则a2+c2+ac-b2的值 ( )
A.大于0 B.小于0 C.等于0 D.不确定
【解析】选C.cos B=
所以a2+c2-b2=-ac,即a2+c2+ac-b2=-ac+ac=0.
3.已知三角形的三边长度分别为6,3 ,3 ,则三角形的最大内角的度数
为 ( )
A.90° B.120° C.135° D.150°
【解析】选C.因为三角形的三边长度6,3 ,3 中,3 是最大的边,
则三角形的最大内角θ满足cos θ=
所以θ=135°.
4.在△ABC中,A=60°,最大边和最小边是方程x2-9x+8=0的两个正实数根,
则边BC=________.?
【解析】因为A=60°,所以最大边和最小边所夹的角为A,AB,AC为x2-9x+8=0
的两个正实数根,
则AB+AC=9,AB×AC=8,所以BC2=AB2+AC2-2×AC×AB×cos A=
(AB+AC)2-2×AC×AB×(1+cos A)=92-2×8× =57.所以BC= .
答案:
