9.1.1正弦定理 课件 2020-2021学年高一下学期数学人教B版(2019)必修第四册(36张PPT)
文档属性
| 名称 | 9.1.1正弦定理 课件 2020-2021学年高一下学期数学人教B版(2019)必修第四册(36张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 721.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 10:01:10 | ||
图片预览










文档简介
第九章 解 三 角 形
9.1 正弦定理与余弦定理
9.1.1 正 弦 定 理
新课程标准
素养风向标
1.通过对任意三角形的边长与角度关系的探索掌握正弦定理.
2.能解决一些简单的三角形度量问题.
1.通过直角三角形的边角关系推广到斜三角形的边角关系.(数学抽象)
2.通过三角形的面积公式计算得到正弦定
理.(数学建模)
3.利用正弦定理计算三角形的边和角或者证明.(数学运算)
基础预习初探
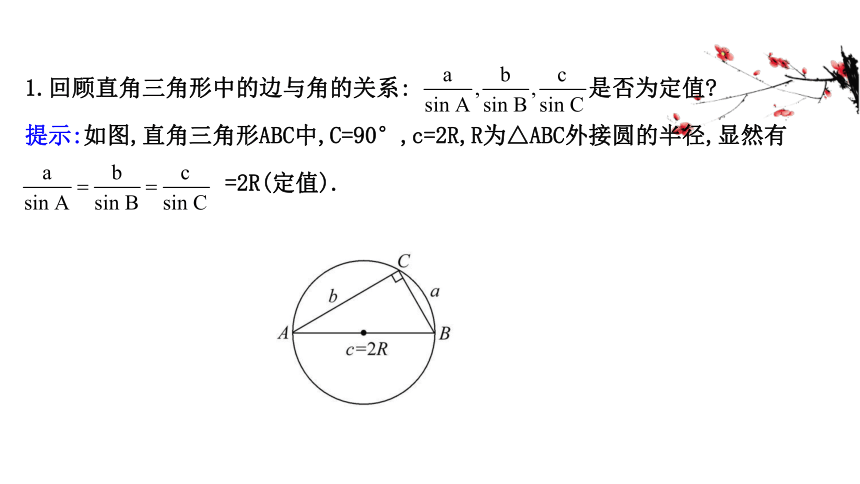
1.回顾直角三角形中的边与角的关系: 是否为定值?
提示:如图,直角三角形ABC中,C=90°,c=2R,R为△ABC外接圆的半径,显然有
=2R(定值).
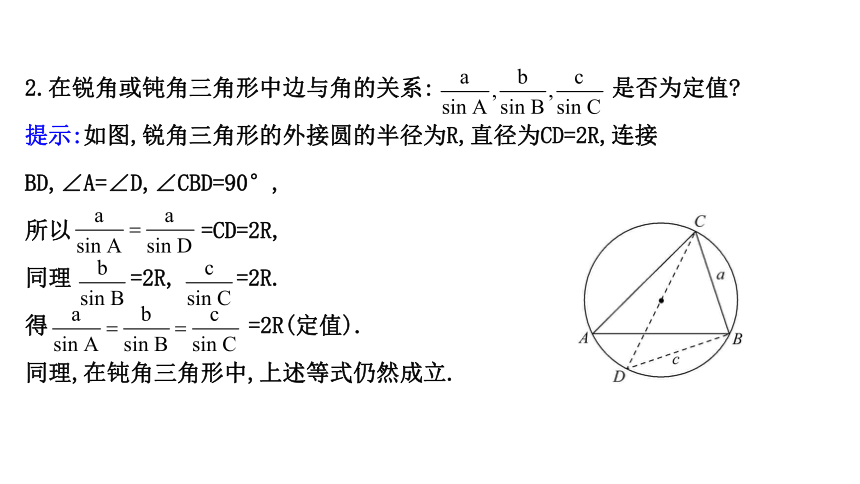
2.在锐角或钝角三角形中边与角的关系: 是否为定值?
提示:如图,锐角三角形的外接圆的半径为R,直径为CD=2R,连接BD,∠A=∠D,∠CBD=90°,
所以 =CD=2R,
同理 =2R, =2R.
得 =2R(定值).
同理,在钝角三角形中,上述等式仍然成立.
3.运用三角形的面积公式如何证明正弦定理?
提示:由三角形的面积公式,得S△ABC= absin C= bcsin A= acsin B,
等式都除以 abc,得
所以
【概念生成】
1.正弦定理
在一个三角形中,各边的长和它所对角的正弦的比相等,即
=2R(R为三角形外接圆的半径)
2.正弦定理的变形公式
由正弦定理,可以得到如下推论(变形公式):
(1)a= ________;(边化角公式)?
b= ________;?
c= ________.?
2Rsin A
2Rsin B
2Rsin C
(2)sin A=____;(角化边公式)
sin B=____;
sin C=____.
3.解三角形
一般地,三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素.已知三
角形的若干元素求其他元素一般称为_________.
解三角形
核心互动探究
探究点一 利用正弦定理解三角形
【典例1】1.在△ABC中,角A,B,C所对的边分别是a,b,c,A=60°,a=4 ,b=4,
则B= ( )
A.30°或150° B.150°
C.30° D.60°
2.已知△ABC中,c=6 cm,A=45°,C=30°,解三角形.
【思维导引】1.由正弦定理求得sin B= ,根据a>b,由三角形中大边对大角
可得B<60°,即可求得B.
2.由A+B+C=180°求角B,再由正弦定理求边长.
【解析】1.选C.因为A=60°,a=4 ,b=4,
由正弦定理 ,得sin B=
因为a>b,所以B<60°,所以B=30°.
2.由三角形内角和定理,得B=180°-(A+C)=105°,
sin 105°=sin 75°=sin(30°+45°)
=sin 30°cos 45°+cos 30°sin 45°=
根据正弦定理 得a= (cm),
b= (cm).
【类题通法】
利用正弦定理解三角形的注意事项
1.如果已知三角形的两角和一边(即ASA或AAS)解三角形,那么通常运用正弦定理计算.
2.注意三角形中大边对大角,大角对大边的关系以及应用.
提醒:注意已知三角形两边和一边的对角即AAS解三角形,三角形可能有0个解或1个解或两个解.解决此类问题通常运用数形结合法.
已知a,b和A,用正弦定理求B时的各种情况如下:
A为锐角
A为钝角或直角
图
形
关系式
①a=bsin A
②a≥b
bsin Aaa>b
a≤b
解的个数
一解
两解
无解
一解
无解
【定向训练】
1.在△ABC中,角A,B,C的对边分别为a,b,c,已知a=1,b= ,A=30°,若B为锐角,
则A∶B∶C= ( )
A.1∶1∶3 B.1∶2∶3
C.1∶3∶2 D.1∶4∶1
【解析】选B.因为a=1,b= ,A=30°,B为锐角,所以由正弦定理得sin B=
,则B=60°,所以C=90°,则A∶B∶C=1∶2∶3.
2.已知△ABC中,a=2 ,c=2 ,A=45°,解三角形.
【解析】因为a=2 ,c=2 ,A=45°,
所以由正弦定理
得sin C=
又0°当C=60°时,B=75°,sin75°=
b=
当C=120°时,B=15°,sin15°= ,
b=
探究点二 利用正弦定理判断三角形的形状
【典例2】1.若 ,则△ABC是 ( )
A.等腰直角三角形
B.有一内角是30°的直角三角形
C. 等边三角形
D. 有一内角是30°的等腰三角形
2.在△ABC中,已知 ,则△ABC的形状是________三角形.?
【思维导引】1.由正弦定理可得tan B=tan C=1,从而判断△ABC的形状.
2.切化弦后,利用正弦定理判断.
【解析】1.选A.在△ABC中, ,
则由正弦定理可得 ,即tan B=tan C=1,
所以B=C=45°,A=90°,故△ABC为等腰直角三角形.
2.由正弦定理得 ,即cos A=cos B,
故A=B,所以△ABC为等腰三角形.
答案:等腰
【类题通法】
判断三角形形状的常用方法及步骤
(1)方法:化边为角或化角为边.
(2)步骤:第一步,将题目中的条件,利用正弦定理化边为角或化角为边,
第二步,根据三角函数的有关知识得到三个内角的关系或三边的关系,进而确定三角形的形状.
【定向训练】
在△ABC中,如果lg a-lg c=lg sin B=-lg ,且B为锐角,试判断此三角形的
形状.
【解题指南】由lg sin B=-lg ,可得sin B= ,求得B=45°.
再由lg a-lg c=-lg 可得 ,可由正弦定理求角.
【解析】因为lg sin B=-lg ,
所以sin B= ,
又因为B是锐角,所以B=45°.
因为lga-lgc=-lg ,
所以 ,
由正弦定理得 ,
得2sin(135°-C)= sin C,
即2(sin 135°cos C-cos 135°sin C)= sin C,
所以cos C=0,所以C=90°,所以A=B=45°,
所以△ABC是等腰直角三角形.
探究点三 计算三角形的面积
【典例3】已知△ABC中,sin Ccos A= ,cos Csin A=- .
(1)求sin A的值.
(2)设AC= ,求△ABC的面积.
【思维导引】(1)由条件联立方程组,消去C得sin A.
或求得sin(C-A)与sin(C+A)再计算sin A.
(2)由正弦定理求BC,再计算S△= absin C.
【解析】(1)方法一:在△ABC中sin Ccos A= ,cos Csin A=- .
得cos C=- ,所以C为钝角,A为锐角.
所以 ,得
两边平方得
整理,得 =0,所以sin2A= ,
又sin A>0,所以sin A= .
方法二:在△ABC中,sin Ccos A= ,cos Csin A=- .所以sin Ccos A-
cos Csin A=1,sin Ccos A+cos Csin A= ,
即sin(C-A)=1,sin(C+A)=sin B= ,
所以C-A= ,且C+A=π-B,所以A=
所以sin A=
所以sin2A= ,又sin A>0,
所以sin A= .
(2)由题知sin B=sin(A+C)=sin Ccos A+cos Csin A=
cos B=
由正弦定理 ,得BC=
又sin C=sin(A+B)=sin Acos B+cos Asin B=
所以S△ABC= AC·BC·sin C=
【类题通法】
求三角形面积的方法
(1)如果已知三角形的两边和夹角(SAS),直接代入三角形的面积公式计算.
(2)如果已知三角形的两角和一边(ASA、AAS),利用正弦定理计算边长,转化为SAS计算三角形的面积.
【定向训练】
已知△ABC的内角A,B,C的对边分别为a,b,c,c=2 ,a>b,C= ,tan A·
tan B=6.
(1)求a,b的值.
(2)计算△ABC的面积.
【解题指南】已知条件已给出tan A·tan B=6,利用两角和的正切公式可得
tan A+tan B,从而可得tan A、tan B的值,进而求得sin A,sin B的值,再利用
正弦定理可求得a,b及三角形的面积.
【解析】(1)由C= ,tan A·tan B=6,
得tan A+tan B=tan(A+B)·(1-tan A·tan B)
=-tan C(1-6)=-tan ×(-5)=5.
又tan A>0,tan B>0,则A,B皆为锐角,又a>b,
则tan A>tan B,得tan A=3,tan B=2.
所以sin A= ,sin B=
由正弦定理得a=
(2)由(1)得S△ABC= absin C=
【补偿训练】
在△ABC中,角A,B,C的对边分别为a,b,c,b=tan B= ,cos A= .
(1)求sin C的值.
(2)求△ABC的面积.
【解题指南】(1)由B= ,cos A= ,
求sin C=sin( -A).
(2)由正弦定理求a,再计算S△= absin C.
【解析】(1)因为A,B,C为△ABC的内角,且tan B= ,得B= ,且cos A= ,
所以C= -A,sin A= ,
所以sin C=
(2)由(1)知sin A= ,sin C= ,
又因为b=tan B= ,所以在△ABC中,由正弦定理,
得a= .所以△ABC的面积S= absin C=
【课堂小结】
课堂素养达标
1.在△ABC中,a= b,A=120°,则角B的大小为 ( )
A.30° B.45° C.60° D.90°
【解析】选A.由正弦定理 得
sin B= ,因为A=120°,得B=30°.
2.在△ABC中,a=bsin A,则△ABC一定是 ( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
【解析】选B.在△ABC中,a=bsin A,由正弦定理,得 =b= ,则sin B=1,
即角B为直角,故△ABC是直角三角形.
3.在△ABC中,A=60°,a= ,b=2,那么满足条件的△ABC ( )
A.有一个解 B.有两个解
C.无解 D.不能确定
【解析】选A.因为b=2,a= ,所以b一解.
4.设△ABC的内角A,B,C的对边分别为a,b,c,且cos A= ,cos B= ,b=3,则
c=________.?
【解析】由已知条件可得sin A= ,sin B= ,
而sin C=sin(A+B)=sin Acos B+cos Asin B= ,
根据正弦定理 ,得c= .
答案:
9.1 正弦定理与余弦定理
9.1.1 正 弦 定 理
新课程标准
素养风向标
1.通过对任意三角形的边长与角度关系的探索掌握正弦定理.
2.能解决一些简单的三角形度量问题.
1.通过直角三角形的边角关系推广到斜三角形的边角关系.(数学抽象)
2.通过三角形的面积公式计算得到正弦定
理.(数学建模)
3.利用正弦定理计算三角形的边和角或者证明.(数学运算)
基础预习初探
1.回顾直角三角形中的边与角的关系: 是否为定值?
提示:如图,直角三角形ABC中,C=90°,c=2R,R为△ABC外接圆的半径,显然有
=2R(定值).
2.在锐角或钝角三角形中边与角的关系: 是否为定值?
提示:如图,锐角三角形的外接圆的半径为R,直径为CD=2R,连接BD,∠A=∠D,∠CBD=90°,
所以 =CD=2R,
同理 =2R, =2R.
得 =2R(定值).
同理,在钝角三角形中,上述等式仍然成立.
3.运用三角形的面积公式如何证明正弦定理?
提示:由三角形的面积公式,得S△ABC= absin C= bcsin A= acsin B,
等式都除以 abc,得
所以
【概念生成】
1.正弦定理
在一个三角形中,各边的长和它所对角的正弦的比相等,即
=2R(R为三角形外接圆的半径)
2.正弦定理的变形公式
由正弦定理,可以得到如下推论(变形公式):
(1)a= ________;(边化角公式)?
b= ________;?
c= ________.?
2Rsin A
2Rsin B
2Rsin C
(2)sin A=____;(角化边公式)
sin B=____;
sin C=____.
3.解三角形
一般地,三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素.已知三
角形的若干元素求其他元素一般称为_________.
解三角形
核心互动探究
探究点一 利用正弦定理解三角形
【典例1】1.在△ABC中,角A,B,C所对的边分别是a,b,c,A=60°,a=4 ,b=4,
则B= ( )
A.30°或150° B.150°
C.30° D.60°
2.已知△ABC中,c=6 cm,A=45°,C=30°,解三角形.
【思维导引】1.由正弦定理求得sin B= ,根据a>b,由三角形中大边对大角
可得B<60°,即可求得B.
2.由A+B+C=180°求角B,再由正弦定理求边长.
【解析】1.选C.因为A=60°,a=4 ,b=4,
由正弦定理 ,得sin B=
因为a>b,所以B<60°,所以B=30°.
2.由三角形内角和定理,得B=180°-(A+C)=105°,
sin 105°=sin 75°=sin(30°+45°)
=sin 30°cos 45°+cos 30°sin 45°=
根据正弦定理 得a= (cm),
b= (cm).
【类题通法】
利用正弦定理解三角形的注意事项
1.如果已知三角形的两角和一边(即ASA或AAS)解三角形,那么通常运用正弦定理计算.
2.注意三角形中大边对大角,大角对大边的关系以及应用.
提醒:注意已知三角形两边和一边的对角即AAS解三角形,三角形可能有0个解或1个解或两个解.解决此类问题通常运用数形结合法.
已知a,b和A,用正弦定理求B时的各种情况如下:
A为锐角
A为钝角或直角
图
形
关系式
①a=bsin A
②a≥b
bsin Aa
a≤b
解的个数
一解
两解
无解
一解
无解
【定向训练】
1.在△ABC中,角A,B,C的对边分别为a,b,c,已知a=1,b= ,A=30°,若B为锐角,
则A∶B∶C= ( )
A.1∶1∶3 B.1∶2∶3
C.1∶3∶2 D.1∶4∶1
【解析】选B.因为a=1,b= ,A=30°,B为锐角,所以由正弦定理得sin B=
,则B=60°,所以C=90°,则A∶B∶C=1∶2∶3.
2.已知△ABC中,a=2 ,c=2 ,A=45°,解三角形.
【解析】因为a=2 ,c=2 ,A=45°,
所以由正弦定理
得sin C=
又0°
b=
当C=120°时,B=15°,sin15°= ,
b=
探究点二 利用正弦定理判断三角形的形状
【典例2】1.若 ,则△ABC是 ( )
A.等腰直角三角形
B.有一内角是30°的直角三角形
C. 等边三角形
D. 有一内角是30°的等腰三角形
2.在△ABC中,已知 ,则△ABC的形状是________三角形.?
【思维导引】1.由正弦定理可得tan B=tan C=1,从而判断△ABC的形状.
2.切化弦后,利用正弦定理判断.
【解析】1.选A.在△ABC中, ,
则由正弦定理可得 ,即tan B=tan C=1,
所以B=C=45°,A=90°,故△ABC为等腰直角三角形.
2.由正弦定理得 ,即cos A=cos B,
故A=B,所以△ABC为等腰三角形.
答案:等腰
【类题通法】
判断三角形形状的常用方法及步骤
(1)方法:化边为角或化角为边.
(2)步骤:第一步,将题目中的条件,利用正弦定理化边为角或化角为边,
第二步,根据三角函数的有关知识得到三个内角的关系或三边的关系,进而确定三角形的形状.
【定向训练】
在△ABC中,如果lg a-lg c=lg sin B=-lg ,且B为锐角,试判断此三角形的
形状.
【解题指南】由lg sin B=-lg ,可得sin B= ,求得B=45°.
再由lg a-lg c=-lg 可得 ,可由正弦定理求角.
【解析】因为lg sin B=-lg ,
所以sin B= ,
又因为B是锐角,所以B=45°.
因为lga-lgc=-lg ,
所以 ,
由正弦定理得 ,
得2sin(135°-C)= sin C,
即2(sin 135°cos C-cos 135°sin C)= sin C,
所以cos C=0,所以C=90°,所以A=B=45°,
所以△ABC是等腰直角三角形.
探究点三 计算三角形的面积
【典例3】已知△ABC中,sin Ccos A= ,cos Csin A=- .
(1)求sin A的值.
(2)设AC= ,求△ABC的面积.
【思维导引】(1)由条件联立方程组,消去C得sin A.
或求得sin(C-A)与sin(C+A)再计算sin A.
(2)由正弦定理求BC,再计算S△= absin C.
【解析】(1)方法一:在△ABC中sin Ccos A= ,cos Csin A=- .
得cos C=- ,所以C为钝角,A为锐角.
所以 ,得
两边平方得
整理,得 =0,所以sin2A= ,
又sin A>0,所以sin A= .
方法二:在△ABC中,sin Ccos A= ,cos Csin A=- .所以sin Ccos A-
cos Csin A=1,sin Ccos A+cos Csin A= ,
即sin(C-A)=1,sin(C+A)=sin B= ,
所以C-A= ,且C+A=π-B,所以A=
所以sin A=
所以sin2A= ,又sin A>0,
所以sin A= .
(2)由题知sin B=sin(A+C)=sin Ccos A+cos Csin A=
cos B=
由正弦定理 ,得BC=
又sin C=sin(A+B)=sin Acos B+cos Asin B=
所以S△ABC= AC·BC·sin C=
【类题通法】
求三角形面积的方法
(1)如果已知三角形的两边和夹角(SAS),直接代入三角形的面积公式计算.
(2)如果已知三角形的两角和一边(ASA、AAS),利用正弦定理计算边长,转化为SAS计算三角形的面积.
【定向训练】
已知△ABC的内角A,B,C的对边分别为a,b,c,c=2 ,a>b,C= ,tan A·
tan B=6.
(1)求a,b的值.
(2)计算△ABC的面积.
【解题指南】已知条件已给出tan A·tan B=6,利用两角和的正切公式可得
tan A+tan B,从而可得tan A、tan B的值,进而求得sin A,sin B的值,再利用
正弦定理可求得a,b及三角形的面积.
【解析】(1)由C= ,tan A·tan B=6,
得tan A+tan B=tan(A+B)·(1-tan A·tan B)
=-tan C(1-6)=-tan ×(-5)=5.
又tan A>0,tan B>0,则A,B皆为锐角,又a>b,
则tan A>tan B,得tan A=3,tan B=2.
所以sin A= ,sin B=
由正弦定理得a=
(2)由(1)得S△ABC= absin C=
【补偿训练】
在△ABC中,角A,B,C的对边分别为a,b,c,b=tan B= ,cos A= .
(1)求sin C的值.
(2)求△ABC的面积.
【解题指南】(1)由B= ,cos A= ,
求sin C=sin( -A).
(2)由正弦定理求a,再计算S△= absin C.
【解析】(1)因为A,B,C为△ABC的内角,且tan B= ,得B= ,且cos A= ,
所以C= -A,sin A= ,
所以sin C=
(2)由(1)知sin A= ,sin C= ,
又因为b=tan B= ,所以在△ABC中,由正弦定理,
得a= .所以△ABC的面积S= absin C=
【课堂小结】
课堂素养达标
1.在△ABC中,a= b,A=120°,则角B的大小为 ( )
A.30° B.45° C.60° D.90°
【解析】选A.由正弦定理 得
sin B= ,因为A=120°,得B=30°.
2.在△ABC中,a=bsin A,则△ABC一定是 ( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
【解析】选B.在△ABC中,a=bsin A,由正弦定理,得 =b= ,则sin B=1,
即角B为直角,故△ABC是直角三角形.
3.在△ABC中,A=60°,a= ,b=2,那么满足条件的△ABC ( )
A.有一个解 B.有两个解
C.无解 D.不能确定
【解析】选A.因为b=2,a= ,所以b
4.设△ABC的内角A,B,C的对边分别为a,b,c,且cos A= ,cos B= ,b=3,则
c=________.?
【解析】由已知条件可得sin A= ,sin B= ,
而sin C=sin(A+B)=sin Acos B+cos Asin B= ,
根据正弦定理 ,得c= .
答案:
