10.1.1复数的概念 课件 2020-2021学年高一下学期数学人教B版(2019)必修第四册(35张PPT)
文档属性
| 名称 | 10.1.1复数的概念 课件 2020-2021学年高一下学期数学人教B版(2019)必修第四册(35张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 541.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 10:03:50 | ||
图片预览










文档简介
第十章 复 数
10.1 复数及其几何意义
10.1.1 复数的概念
新课程标准
素养风向标
1.在问题情境中了解数系的扩充过程,体会实际需求与数学内部的矛盾(数的运算规则、方程求根)在数系扩充过程中的作用,感受人类理性思维的作用以及数与现实世界的联系.
2.理解复数的基本概念以及复数相等的充要条件.
1.通过数系的扩充引入复数的有关概念.(数学抽象)
2.通过数系的扩充构建数系表,形成知识网络.(数学建模)
3.利用复数的实部虚部的关系建立复数相等的意义.(逻辑推理)
基础预习初探
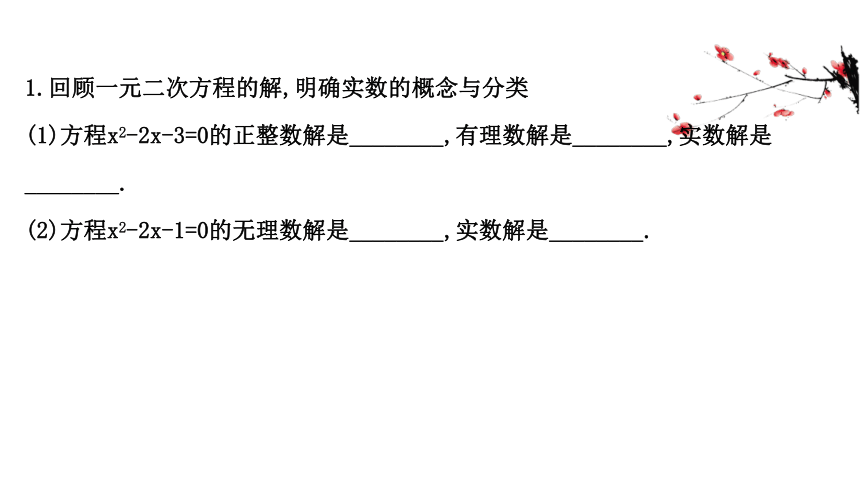
1.回顾一元二次方程的解,明确实数的概念与分类
(1)方程x2-2x-3=0的正整数解是________,有理数解是________,实数解是________.?
(2)方程x2-2x-1=0的无理数解是________,实数解是________.?
提示:(1)方程x2-2x-3=0即(x-3)(x+1)=0的正整数解是3,有理数解是3,-1,
实数解是3,-1.
(2)方程x2-2x-1=0的无理数解是 ,实数解是 .
答案:(1)3 3,-1 3,-1
(2)
2.(1)方程x2=-1在实数集中是否有解?
(2)如何解决方程无实数解的问题?
提示:(1)因为实数的平方都是非负数,所以方程x2=-1在实数集中无解.
(2)引入新数i,定义i·i=i2=-1,那么方程x2=-1有一个解为i.
3.(1)复数a+bi(a,b∈R)何时表示零?
提示:当且仅当a=b=0时表示零.
(2)实数集R与复数集C有什么关系?
提示:用文字语言描述:实数集R是复数集C的真子集,
即R C.
用图形语言描述:
【概念生成】
1.复数的概念:
(1)复数的定义
一般地,当a与b都是实数时,称a+bi为复数,其中i叫做_________,满足i2=___,
全体复数组成的集合C叫做_______.
虚数单位
-1
复数集
(2)复数的表示
复数通常用字母z表示,即z=_____________,这一表示形式叫做复数的_______
___,a与b分别叫做复数z的_____与_____.
分别记作Re(z)=__,Im(z)=__.
2.复数相等
如果a,b,c,d都是实数,那么a+bi=c+di?_________.
特别地,当a,b都是实数时,a+bi=0的充要条件是a=0且b=0.
a+bi(a,b∈R)
代数形
式
实部
虚部
a=c且b=d
a
b
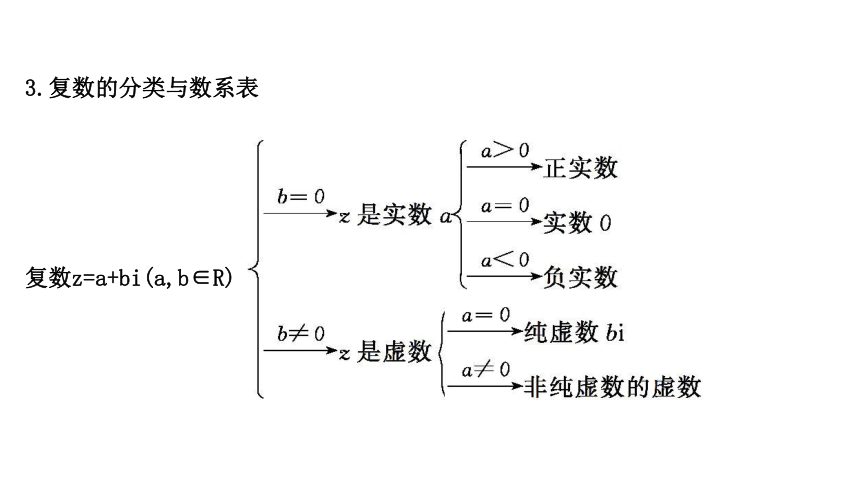
3.复数的分类与数系表
复数z=a+bi(a,b∈R)
核心互动探究
探究点一 复数的有关概念与表示
【典例1】1.下列复数中虚数的个数为 ( )
1+2i,1+2i2,2i+ ,πi.
A.1 B.2 C.3 D.4
2.已知虚数z=(a+b)+(a-b)i,且实部与虚部互为相反数,则实数a,b满足的条件
是________.?
【思维导引】1.利用复数的概念进行判断.
2.根据复数的概念与表示?复数的实部+虚部=0.
【解析】1.选C.1+2i,πi,2i+ 是虚数,1+2i2=-1是实数.
2.虚数z=(a+b)+(a-b)i,且实部与虚部互为相反数,得(a+b)+(a-b)=0,
得a=0,b∈R,且b≠0.
所以实数a,b满足的条件是a=0,b∈R,且b≠0.
答案:a=0,b∈R,且b≠0
【类题通法】判断与复数有关的命题是否正确的策略
(1)复数的代数形式:
若z=a+bi,只有当a,b∈R时,a才是z的实部,b才是z的虚部,且注意虚部不是bi,而是b.
(2)不要将复数与虚数的概念混淆,实数也是复数,实数和虚数是复数的两大构成部分.
(3)举反例:判断一个命题为假命题,只要举一个反例即可,所以解答这类题时,可按照“先特殊,后一般,先否定,后肯定”的方法进行解答.
【定向训练】
1.复数z=2-3i的虚部为 ( )
A.3i B.-3i C.3 D.-3
【解析】选D.因为z=2-3i,所以z的虚部为-3.
2.已知复数z=(a-1)-(2-b)i的实部和虚部分别是2和1,则实数a,b的值分别是________.?
【解析】由题意得:a-1=2,-(2-b)=1,所以a=3,b=3.
答案:3,3
探究点二 复数的分类与参数问题
【典例2】1.已知复数z=(x2-1)+(x+1)i(x∈R)为纯虚数,则z=________;?
2.已知m∈R,复数z= ,
当m为何值时,z分别满足下列条件:
(1)z∈R;(2)z是虚数;(3)z是纯虚数.
【思维导引】当a,b都是实数时,
【解析】1.由于复数z=(x2-1)+(x+1)i为纯虚数,
则实数x满足 ,解得x=1,所以z=2i.
答案:2i
2.复数z= ,m∈R.
(1)由z∈R,得 解得m=-3.
(2)由z是虚数,得m2+2m-3≠0且m-1≠0,
解得m≠1且m≠-3.
(3)由z是纯虚数,得
解得m=0或m=-2.
【类题通法】
1.解决复数分类问题的方法与步骤
(1)化标准式:解题时一定要先看复数是否为a+bi(a,b∈R)的形式,以确定实部和虚部.
(2)定条件:复数的分类问题可以转化为复数的实部与虚部应该满足的条件问题,列出实部和虚部满足的方程(不等式)组即可.
(3)下结论:设所给复数为z=a+bi(a,b∈R),①z为实数?b=0;②z为虚数?b≠0;③z为纯虚数?a=0且b≠0.
2.复数分类的应用
(1)参数自身:判断一个含有参数的复数在什么情况下是实数、虚数、纯虚数,首先要保证参数值使表达式有意义,其次对参数值的取舍,是取“并”还是“交”,非常关键,解答后进行验算是很必要的.
(2)整体与局部:对于复数z=a+bi(a,b∈R),既要从整体的角度去认识它,把复数z看成一个整体,又要从实部与虚部的角度分解成两部分去认识它.这是解复数问题的重要思路之一.
【定向训练】
已知复数z=(m2+5m+6)+(m2-2m-15)i:
(1)若复数z是实数,求实数m的值;
(2)若复数z是虚数,求实数m的取值范围;
(3)若复数z是纯虚数,求实数m的值;
(4)若复数z是0,求实数m的值.
【解析】(1)当m2-2m-15=0时,复数z为实数,
所以m=5或-3.
(2)当m2-2m-15≠0时复数z为虚数,
所以m≠5且m≠-3.
所以实数m的取值范围为{m|m≠5且m≠-3}.
(3)当 时,复数z是纯虚数,所以m=-2.
(4)当 时,复数z是0,所以m=-3.
【补偿训练】
下列复数中,实数为________,虚数为________,纯虚数为________.(将序号填在相应的横线上)?
①1-2i2;②-3i;③2i-3;
④1+0i;⑤cos π+isin π.
【解析】-3i,2i-3是虚数;-3i是纯虚数;1-2i2=3,1+0i=1,cos π+isin π=-1,都是实数.
答案:①④⑤ ②③ ②
探究点三 复数相等及其应用
【典例3】1.已知复数z1=a+2i,z2=2+2bi,若z1=z2,则实数a,b的值分别为 ( )
A.a=1,b=1 B.a=1,b=2
C.a=2,b=1 D.a=2,b=2
2.已知关于x的方程(x2+x+3m)-(2x+1)i=0有实数根,求实数m的值及方程的实数根.
【思维导引】1.根据复数相等的充要条件:实部与虚部分别相等求a,b的值.
2.设出方程的实数解,代入原式整理为a+bi=0(a,b∈R)的形式解决.
【解析】1.选C.因为复数z1=a+2i,z2=2+2bi,且z1=z2,则实数a=2,2b=2,
即a=2,b=1.
2.设a是原方程的实数根,
即(a2+a+3m)-(2a+1)i=0+0i,
所以a2+a+3m=0且2a+1=0,
所以a= 且 +3m=0,
所以m= .
所以m= ,方程的实数根为x= .
【类题通法】
复数相等问题的解题技巧
(1)必须是复数的代数形式才可以根据实部与实部相等,虚部与虚部相等列方程组求解.
(2)根据复数相等的条件,将复数问题转化为实数问题,为应用方程思想提供了条件,同时这也是复数问题实数化思想的体现.
(3)如果两个复数都是实数,可以比较大小,否则是不能比较大小的.
【定向训练】
已知θ为三角形的内角,复数z1=sin 2θ-icos θ,z2=cos θ+i sin θ,若z1=z2,则θ=________.?
【解析】依题意,得 ,
即 ,显然cos θ≠0,
所以 ,
又因为θ为三角形的内角,所以θ= .
答案:
【补偿训练】
求适合等式(2x-1)+i=y+(y-3)i的x,y的值,其中x∈R,y∈R.
【解析】由复数相等的充要条件可知
解得
【课堂小结】
课堂素养达标
1.若集合A={-1,0,1,i},i是虚数单位,则 ( )
A.i?A B.i2∈A
C.1+i∈A D.2i∈A
【解析】选B.由于集合A={-1,0,1,i},i是虚数单位,
则i∈A,i2=-1∈A,1+i?A,2i?A.
2.复数z=2-i的实部与虚部分别为 ( )
A.2 1 B.2 -1
C.2 i D.2 -i
【解析】选B.复数z=2-i=2+(-i)的实部为2,虚部为-1.
3.如果C,R,I分别表示复数集、实数集和纯虚数集,则 ( )
A.C=R∪I B.R∪I={0}
C.R=C∩I D.R∩I= ?
【解析】选D.复数包括实数和虚数,所以实数集与纯虚数集无交集.
所以R∩I=?.
4.如果x-1+yi与i-3x为相等复数,x,y为实数,则x=________,y=________.?
【解析】由复数相等可知 所以
答案: 1
10.1 复数及其几何意义
10.1.1 复数的概念
新课程标准
素养风向标
1.在问题情境中了解数系的扩充过程,体会实际需求与数学内部的矛盾(数的运算规则、方程求根)在数系扩充过程中的作用,感受人类理性思维的作用以及数与现实世界的联系.
2.理解复数的基本概念以及复数相等的充要条件.
1.通过数系的扩充引入复数的有关概念.(数学抽象)
2.通过数系的扩充构建数系表,形成知识网络.(数学建模)
3.利用复数的实部虚部的关系建立复数相等的意义.(逻辑推理)
基础预习初探
1.回顾一元二次方程的解,明确实数的概念与分类
(1)方程x2-2x-3=0的正整数解是________,有理数解是________,实数解是________.?
(2)方程x2-2x-1=0的无理数解是________,实数解是________.?
提示:(1)方程x2-2x-3=0即(x-3)(x+1)=0的正整数解是3,有理数解是3,-1,
实数解是3,-1.
(2)方程x2-2x-1=0的无理数解是 ,实数解是 .
答案:(1)3 3,-1 3,-1
(2)
2.(1)方程x2=-1在实数集中是否有解?
(2)如何解决方程无实数解的问题?
提示:(1)因为实数的平方都是非负数,所以方程x2=-1在实数集中无解.
(2)引入新数i,定义i·i=i2=-1,那么方程x2=-1有一个解为i.
3.(1)复数a+bi(a,b∈R)何时表示零?
提示:当且仅当a=b=0时表示零.
(2)实数集R与复数集C有什么关系?
提示:用文字语言描述:实数集R是复数集C的真子集,
即R C.
用图形语言描述:
【概念生成】
1.复数的概念:
(1)复数的定义
一般地,当a与b都是实数时,称a+bi为复数,其中i叫做_________,满足i2=___,
全体复数组成的集合C叫做_______.
虚数单位
-1
复数集
(2)复数的表示
复数通常用字母z表示,即z=_____________,这一表示形式叫做复数的_______
___,a与b分别叫做复数z的_____与_____.
分别记作Re(z)=__,Im(z)=__.
2.复数相等
如果a,b,c,d都是实数,那么a+bi=c+di?_________.
特别地,当a,b都是实数时,a+bi=0的充要条件是a=0且b=0.
a+bi(a,b∈R)
代数形
式
实部
虚部
a=c且b=d
a
b
3.复数的分类与数系表
复数z=a+bi(a,b∈R)
核心互动探究
探究点一 复数的有关概念与表示
【典例1】1.下列复数中虚数的个数为 ( )
1+2i,1+2i2,2i+ ,πi.
A.1 B.2 C.3 D.4
2.已知虚数z=(a+b)+(a-b)i,且实部与虚部互为相反数,则实数a,b满足的条件
是________.?
【思维导引】1.利用复数的概念进行判断.
2.根据复数的概念与表示?复数的实部+虚部=0.
【解析】1.选C.1+2i,πi,2i+ 是虚数,1+2i2=-1是实数.
2.虚数z=(a+b)+(a-b)i,且实部与虚部互为相反数,得(a+b)+(a-b)=0,
得a=0,b∈R,且b≠0.
所以实数a,b满足的条件是a=0,b∈R,且b≠0.
答案:a=0,b∈R,且b≠0
【类题通法】判断与复数有关的命题是否正确的策略
(1)复数的代数形式:
若z=a+bi,只有当a,b∈R时,a才是z的实部,b才是z的虚部,且注意虚部不是bi,而是b.
(2)不要将复数与虚数的概念混淆,实数也是复数,实数和虚数是复数的两大构成部分.
(3)举反例:判断一个命题为假命题,只要举一个反例即可,所以解答这类题时,可按照“先特殊,后一般,先否定,后肯定”的方法进行解答.
【定向训练】
1.复数z=2-3i的虚部为 ( )
A.3i B.-3i C.3 D.-3
【解析】选D.因为z=2-3i,所以z的虚部为-3.
2.已知复数z=(a-1)-(2-b)i的实部和虚部分别是2和1,则实数a,b的值分别是________.?
【解析】由题意得:a-1=2,-(2-b)=1,所以a=3,b=3.
答案:3,3
探究点二 复数的分类与参数问题
【典例2】1.已知复数z=(x2-1)+(x+1)i(x∈R)为纯虚数,则z=________;?
2.已知m∈R,复数z= ,
当m为何值时,z分别满足下列条件:
(1)z∈R;(2)z是虚数;(3)z是纯虚数.
【思维导引】当a,b都是实数时,
【解析】1.由于复数z=(x2-1)+(x+1)i为纯虚数,
则实数x满足 ,解得x=1,所以z=2i.
答案:2i
2.复数z= ,m∈R.
(1)由z∈R,得 解得m=-3.
(2)由z是虚数,得m2+2m-3≠0且m-1≠0,
解得m≠1且m≠-3.
(3)由z是纯虚数,得
解得m=0或m=-2.
【类题通法】
1.解决复数分类问题的方法与步骤
(1)化标准式:解题时一定要先看复数是否为a+bi(a,b∈R)的形式,以确定实部和虚部.
(2)定条件:复数的分类问题可以转化为复数的实部与虚部应该满足的条件问题,列出实部和虚部满足的方程(不等式)组即可.
(3)下结论:设所给复数为z=a+bi(a,b∈R),①z为实数?b=0;②z为虚数?b≠0;③z为纯虚数?a=0且b≠0.
2.复数分类的应用
(1)参数自身:判断一个含有参数的复数在什么情况下是实数、虚数、纯虚数,首先要保证参数值使表达式有意义,其次对参数值的取舍,是取“并”还是“交”,非常关键,解答后进行验算是很必要的.
(2)整体与局部:对于复数z=a+bi(a,b∈R),既要从整体的角度去认识它,把复数z看成一个整体,又要从实部与虚部的角度分解成两部分去认识它.这是解复数问题的重要思路之一.
【定向训练】
已知复数z=(m2+5m+6)+(m2-2m-15)i:
(1)若复数z是实数,求实数m的值;
(2)若复数z是虚数,求实数m的取值范围;
(3)若复数z是纯虚数,求实数m的值;
(4)若复数z是0,求实数m的值.
【解析】(1)当m2-2m-15=0时,复数z为实数,
所以m=5或-3.
(2)当m2-2m-15≠0时复数z为虚数,
所以m≠5且m≠-3.
所以实数m的取值范围为{m|m≠5且m≠-3}.
(3)当 时,复数z是纯虚数,所以m=-2.
(4)当 时,复数z是0,所以m=-3.
【补偿训练】
下列复数中,实数为________,虚数为________,纯虚数为________.(将序号填在相应的横线上)?
①1-2i2;②-3i;③2i-3;
④1+0i;⑤cos π+isin π.
【解析】-3i,2i-3是虚数;-3i是纯虚数;1-2i2=3,1+0i=1,cos π+isin π=-1,都是实数.
答案:①④⑤ ②③ ②
探究点三 复数相等及其应用
【典例3】1.已知复数z1=a+2i,z2=2+2bi,若z1=z2,则实数a,b的值分别为 ( )
A.a=1,b=1 B.a=1,b=2
C.a=2,b=1 D.a=2,b=2
2.已知关于x的方程(x2+x+3m)-(2x+1)i=0有实数根,求实数m的值及方程的实数根.
【思维导引】1.根据复数相等的充要条件:实部与虚部分别相等求a,b的值.
2.设出方程的实数解,代入原式整理为a+bi=0(a,b∈R)的形式解决.
【解析】1.选C.因为复数z1=a+2i,z2=2+2bi,且z1=z2,则实数a=2,2b=2,
即a=2,b=1.
2.设a是原方程的实数根,
即(a2+a+3m)-(2a+1)i=0+0i,
所以a2+a+3m=0且2a+1=0,
所以a= 且 +3m=0,
所以m= .
所以m= ,方程的实数根为x= .
【类题通法】
复数相等问题的解题技巧
(1)必须是复数的代数形式才可以根据实部与实部相等,虚部与虚部相等列方程组求解.
(2)根据复数相等的条件,将复数问题转化为实数问题,为应用方程思想提供了条件,同时这也是复数问题实数化思想的体现.
(3)如果两个复数都是实数,可以比较大小,否则是不能比较大小的.
【定向训练】
已知θ为三角形的内角,复数z1=sin 2θ-icos θ,z2=cos θ+i sin θ,若z1=z2,则θ=________.?
【解析】依题意,得 ,
即 ,显然cos θ≠0,
所以 ,
又因为θ为三角形的内角,所以θ= .
答案:
【补偿训练】
求适合等式(2x-1)+i=y+(y-3)i的x,y的值,其中x∈R,y∈R.
【解析】由复数相等的充要条件可知
解得
【课堂小结】
课堂素养达标
1.若集合A={-1,0,1,i},i是虚数单位,则 ( )
A.i?A B.i2∈A
C.1+i∈A D.2i∈A
【解析】选B.由于集合A={-1,0,1,i},i是虚数单位,
则i∈A,i2=-1∈A,1+i?A,2i?A.
2.复数z=2-i的实部与虚部分别为 ( )
A.2 1 B.2 -1
C.2 i D.2 -i
【解析】选B.复数z=2-i=2+(-i)的实部为2,虚部为-1.
3.如果C,R,I分别表示复数集、实数集和纯虚数集,则 ( )
A.C=R∪I B.R∪I={0}
C.R=C∩I D.R∩I= ?
【解析】选D.复数包括实数和虚数,所以实数集与纯虚数集无交集.
所以R∩I=?.
4.如果x-1+yi与i-3x为相等复数,x,y为实数,则x=________,y=________.?
【解析】由复数相等可知 所以
答案: 1
