10.1.2复数的几何意义 课件 2020-2021学年高一下学期数学人教B版(2019)必修第四册(35张PPT)
文档属性
| 名称 | 10.1.2复数的几何意义 课件 2020-2021学年高一下学期数学人教B版(2019)必修第四册(35张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 533.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 00:00:00 | ||
图片预览











文档简介
10.1.2 复数的几何意义
新课程标准
素养风向标
了解复数的代数表示及其几何意义,会用复平面内的点和平面向量来表示复数.
1.通过复数的几何意义领会数形结合的思想.(直观想象、数学抽象)
2.通过构造平面向量将复数转化为图形解决问题.(数学建模)
3.利用复数的几何意义计算复数的模,明确轨迹的形状.(逻辑推理)
基础预习初探
1.回顾平面直角坐标系与点的坐标
(1)在平面直角坐标系xOy中,O为原点,点Z(a,b)对应的向量 =________,对应的复数z=________.?
(2)在复平面内,复数z=a+bi,a,b∈R,对应的点Z的坐标为________,对应的向量 =________.?
提示:(1)(a,b) a+bi
(2)(a,b) (a,b)
2.若复数z=a+bi(a,b∈R)对应的点位于复平面内的第三象限,则复数的实部与
虚部满足什么条件?
提示:当a<0,b<0时,复数对应的点位于复平面内的第三象限.
3.(1)设Z(a,b),则向量 的模如何用a,b表示?
提示:| |= .
(2)复数可以用向量表示,那么向量的模是复数的什么?
提示:用文字语言描述:向量的模就是复数的模.
用符号语言描述:|z|=| |= .
4.复数z=a+bi与复数 =a-bi对应的点有什么关系?
提示:复数z=a+bi对应的点为(a,b),复数 =a-bi对应的点为(a,-b),两点关于
x轴对称.特别地,当b=0时,两点重合.
【概念生成】
1.复平面
如图,把建立了___________来表示复数的平面叫做复平面,x轴称为___轴,y轴
称为___轴.实轴上的点对应的都表示实数,除_____外,虚轴上的点对应的都表
示纯虚数.
直角坐标系
实
虚
原点
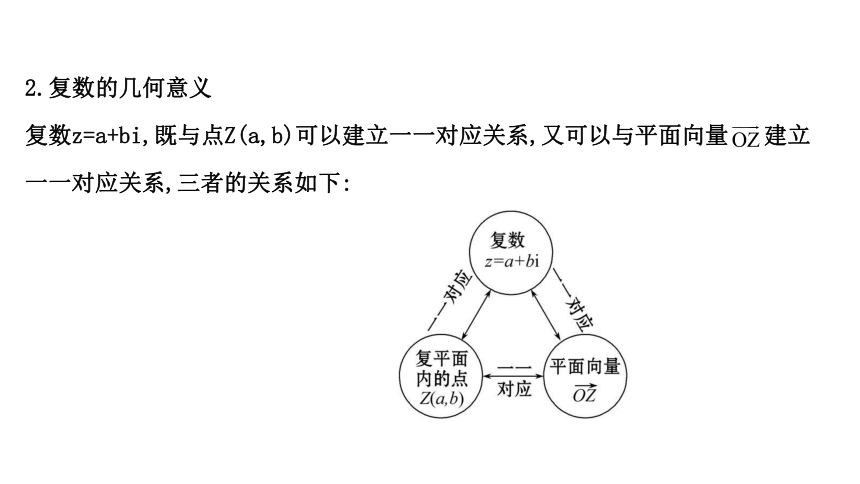
2.复数的几何意义
复数z=a+bi,既与点Z(a,b)可以建立一一对应关系,又可以与平面向量 建立一一对应关系,三者的关系如下:
3.复数的模(或绝对值)
一般地,向量 =(a,b)的长度称为复数z=a+bi的模(或绝对值),记作|z|或
|a+bi|.
如果b=0,那么z=a+bi就是实数a,它的模等于|a|(即实数a的绝对值).
|z|=|a+bi|=________.
4.共轭复数
一般地,如果两个复数的实部_____,虚部互为_____数,则称这两个复数互为共
轭复数.复数z的共轭复数用 表示,因此,当z=a+bi(a,b∈R)时,有 =a-bi.
相等
相反
核心互动探究
探究点一 复数与点的一一对应
【典例1】1.在复平面内,复数4+5i,-2+i对应的点分别为A,B,若C为线段AB的中点,则点C对应的复数是 ( )
A.1+2i B.1+3i
C.3+3i D.3+4i
2.实数m取什么值时,复平面内表示复数z=(m2-8m+15)+(m2-5m-14)i的点:
(1)位于第四象限;(2)位于直线y=x上.
【思维导引】1.利用相等向量计算,也可以利用线段的中点坐标公式计算;
2.根据点的位置列方程或不等式组求解.
【解析】1.选B.方法一:在复平面内,复数4+5i,-2+i对应的点分别为A(4,5),
B(-2,1),设线段AB的中点C为(x,y),则 ,即(x-4,y-5)=(-2-x,1-y),
得x-4=-2-x,y-5=1-y,
解得x=1,y=3.
所以C(1,3)对应的复数为1+3i.
方法二:复数4+5i,-2+i对应的点分别为A(4,5),B(-2,1),则线段AB的中点
C(1,3),所以C(1,3)对应的复数为1+3i.
2.(1)由 ?
所以-2(2)要使z对应的点在直线y=x上,需m2-8m+15=m2-5m-14,解得m= .
【类题通法】
复数与点的对应关系及应用
(1)复平面内复数与点的对应关系的实质是:复数的实部就是该点的横坐标,虚部就是该点的纵坐标.
(2)已知复数在复平面内对应的点满足的条件求参数的取值范围时,可根据复数与点的对应关系,建立复数的实部与虚部满足的条件构成的方程(组)或不等式(组),通过解方程(组)或不等式(组)得出结论.
【定向训练】
1.当A.第一象限 B.第二象限
C.第三象限 D.第四象限
【解析】选D.复数z在复平面内对应的点为Z(5m-2,m-2).由得5m-2>0,m-2<0.所以点Z位于第四象限.
2.实数m取什么值时,复数z=2m+(4-m2)i在复平面内对应的点在:
(1)虚轴上;
(2)第一、三象限;
(3)以原点为圆心,4为半径的圆上.
【解析】(1)若复数z在复平面内的对应点位于虚轴上,
则2m=0,即m=0.
(2)若复数z在复平面内对应的点位于第一、三象限,
则2m(4-m2)>0,解得m<-2或0(3)若复数z对应的点位于以原点为圆心,4为半径的圆上,
则 =4,即m4-4m2=0,解得m=0或m=±2.
探究点二 复数与向量的一一对应
【典例2】1.已知A(1,2),B(-3,5),则向量 对应的复数为 ( )
A.1+2i B.-3+5i
C.-2+7i D.-4+3i
2.已知O为坐标原点,向量 对应的复数是4+3i,点A关于实轴的对称点为A1,
将向量 平移,使其起点移动到A点,这时终点为A2.
(1)求向量 对应的复数;
(2)求点A2对应的复数.
【思维导引】1.求出向量 的坐标,再确定对应的复数.
2.根据复数与点以及复数与向量的对应关系求解.
【解析】1.选D.由于A(1,2),B(-3,5),
则向量 =(-4,3),所以 对应的复数为-4+3i.
2.(1)因为向量 对应的复数是4+3i,
所以点A对应的复数也是4+3i,
因此点A坐标为(4,3),
所以点A关于实轴的对称点A1为(4,-3),
故向量 对应的复数是4-3i.
(2)依题意知 = ,而 =(4,-3),
设A2(x,y),则有(4,-3)=(x-4,y-3),
所以x=8,y=0,即A2(8,0).
所以点A2对应的复数是8.
【类题通法】
复数与向量的对应关系的两个关注点
(1)复数z=a+bi(a,b∈R)是与以原点为起点,Z(a,b)为终点的向量 一一对
应的.
(2)一个向量可以平移,其对应的复数不变,但是其起点与终点所对应的复数可
能改变.
提醒:向量是自由向量,其长度与方向与起点的位置无关, =(xB-xA,yB-yA),
对应的复数的实部和虚部分别是向量的横坐标和纵坐标.
【定向训练】
在复平面内,O为原点,向量 对应的复数为-1+2i,若点A关于直线y=-x的对
称点为点B,则向量 对应的复数为 ( )
A.-2-i B.-2+i
C.1+2i D.-1+2i
【解析】选B.因为复数-1+2i对应的点为A(-1,2),点A关于直线y=-x的对称点
为B(-2,1),
所以 对应的复数为-2+i.
【补偿训练】
已知平面直角坐标系中O是原点,向量 , 对应的复数分别为2-3i,-3+2i,
那么向量 对应的复数是________.?
【解析】向量 , 对应的复数分别为2-3i,-3+2i,根据复数与复平面内的
点一一对应,可得向量 =(2,-3), =(-3,2).
由向量减法的坐标运算可得向量 =(2+3,-3-2)=(5,-5),根据复数
与复平面内的点一一对应,可得向量 对应的复数是5-5i.
答案:5-5i
探究点三 共轭复数与复数的模
【典例3】1.已知复数z与复数z1=3-4i的模相等且与复数z2=a+5i互为共轭复数,则z= ( )
A.3+4i B.3-5i
C.5i D.-5i
2.已知z∈C,|z|=5,求z表示的点的轨迹.
【思维导引】1.两个共轭复数实部相等,虚部互为相反数,且二者的模相等.
2.设复数z对应向量 ,其中O为原点,根据圆的定义判断轨迹形状.
【解析】1.选D.因为复数z与复数z1=3-4i的模相等且与复数z2=a+5i互为共轭
复数,则|z|=|z1|=|z2|,得 = =5,所以a=0,z2=5i,z= =-5i.
2.设复数z对应向量 ,其中O为原点,根据|z|=5,得| |=5,由圆的定义,动
点Z的轨迹是以O为圆心,5为半径的圆,即复数z表示的点的轨迹是圆.
【类题通法】
关于复数的模的两个关注点
1.复数的模表示对应向量的长度,也就是对应的两点之间的距离.
2.注意复平面上两点间的距离公式的多角度应用:
设z1=a+bi,z2=c+di, =(a,b), =(c,d),
则 .
【定向训练】
1.已知复数z1=-2+i,z2=1-3i,对应的点分别为A,B,则向量| |=________.?
【解析】复数z1=-2+i,z2=1-3i,对应的点分别为A(-2,1),B(1,-3),
则向量 =(3,-4),所以| |=5.
答案:5
2.已知3-4i=x+yi(x,y∈R),则|1-5i|,|x-yi|,|y+2i|的大小关系为____________.?
【解析】由3-4i=x+yi(x,y∈R),
得x=3,y=-4.
而|1-5i|=
|x-yi|=|3+4i|= =5,
|y+2i|=|-4+2i|=
因为 <5< ,
所以|y+2i|<|x-yi|<|1-5i|.
答案:|y+2i|<|x-yi|<|1-5i|
【课堂小结】
课堂素养达标
1.在复平面内,复数z=4-5i对应的点的坐标为 ( )
A.(4,5) B.(4,-5)
C.(5,4) D.(-5,4)
【解析】选B.复数z=4-5i对应的点的坐标为(4,-5).
2.在复平面内,复数z=sin 2+icos 2对应的点位于 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【解析】选D.因为 <2<π,所以sin 2>0,cos 2<0.
故z=sin 2+icos 2对应的点在第四象限.
3.已知复数z满足|z|2-2|z|-3=0,则复数z对应点的轨迹为 ( )
A.一个圆 B.线段
C.两点 D.两个圆
【解析】选A.因为|z|2-2|z|-3=0,所以(|z|-3)(|z|+1)=0,所以|z|=3.故所求的轨迹为一个圆.
4.复平面内,点(0,-3)对应的复数为________.?
【解析】点(0,-3)对应的复数为-3i.
答案:-3i
新课程标准
素养风向标
了解复数的代数表示及其几何意义,会用复平面内的点和平面向量来表示复数.
1.通过复数的几何意义领会数形结合的思想.(直观想象、数学抽象)
2.通过构造平面向量将复数转化为图形解决问题.(数学建模)
3.利用复数的几何意义计算复数的模,明确轨迹的形状.(逻辑推理)
基础预习初探
1.回顾平面直角坐标系与点的坐标
(1)在平面直角坐标系xOy中,O为原点,点Z(a,b)对应的向量 =________,对应的复数z=________.?
(2)在复平面内,复数z=a+bi,a,b∈R,对应的点Z的坐标为________,对应的向量 =________.?
提示:(1)(a,b) a+bi
(2)(a,b) (a,b)
2.若复数z=a+bi(a,b∈R)对应的点位于复平面内的第三象限,则复数的实部与
虚部满足什么条件?
提示:当a<0,b<0时,复数对应的点位于复平面内的第三象限.
3.(1)设Z(a,b),则向量 的模如何用a,b表示?
提示:| |= .
(2)复数可以用向量表示,那么向量的模是复数的什么?
提示:用文字语言描述:向量的模就是复数的模.
用符号语言描述:|z|=| |= .
4.复数z=a+bi与复数 =a-bi对应的点有什么关系?
提示:复数z=a+bi对应的点为(a,b),复数 =a-bi对应的点为(a,-b),两点关于
x轴对称.特别地,当b=0时,两点重合.
【概念生成】
1.复平面
如图,把建立了___________来表示复数的平面叫做复平面,x轴称为___轴,y轴
称为___轴.实轴上的点对应的都表示实数,除_____外,虚轴上的点对应的都表
示纯虚数.
直角坐标系
实
虚
原点
2.复数的几何意义
复数z=a+bi,既与点Z(a,b)可以建立一一对应关系,又可以与平面向量 建立一一对应关系,三者的关系如下:
3.复数的模(或绝对值)
一般地,向量 =(a,b)的长度称为复数z=a+bi的模(或绝对值),记作|z|或
|a+bi|.
如果b=0,那么z=a+bi就是实数a,它的模等于|a|(即实数a的绝对值).
|z|=|a+bi|=________.
4.共轭复数
一般地,如果两个复数的实部_____,虚部互为_____数,则称这两个复数互为共
轭复数.复数z的共轭复数用 表示,因此,当z=a+bi(a,b∈R)时,有 =a-bi.
相等
相反
核心互动探究
探究点一 复数与点的一一对应
【典例1】1.在复平面内,复数4+5i,-2+i对应的点分别为A,B,若C为线段AB的中点,则点C对应的复数是 ( )
A.1+2i B.1+3i
C.3+3i D.3+4i
2.实数m取什么值时,复平面内表示复数z=(m2-8m+15)+(m2-5m-14)i的点:
(1)位于第四象限;(2)位于直线y=x上.
【思维导引】1.利用相等向量计算,也可以利用线段的中点坐标公式计算;
2.根据点的位置列方程或不等式组求解.
【解析】1.选B.方法一:在复平面内,复数4+5i,-2+i对应的点分别为A(4,5),
B(-2,1),设线段AB的中点C为(x,y),则 ,即(x-4,y-5)=(-2-x,1-y),
得x-4=-2-x,y-5=1-y,
解得x=1,y=3.
所以C(1,3)对应的复数为1+3i.
方法二:复数4+5i,-2+i对应的点分别为A(4,5),B(-2,1),则线段AB的中点
C(1,3),所以C(1,3)对应的复数为1+3i.
2.(1)由 ?
所以-2
【类题通法】
复数与点的对应关系及应用
(1)复平面内复数与点的对应关系的实质是:复数的实部就是该点的横坐标,虚部就是该点的纵坐标.
(2)已知复数在复平面内对应的点满足的条件求参数的取值范围时,可根据复数与点的对应关系,建立复数的实部与虚部满足的条件构成的方程(组)或不等式(组),通过解方程(组)或不等式(组)得出结论.
【定向训练】
1.当
C.第三象限 D.第四象限
【解析】选D.复数z在复平面内对应的点为Z(5m-2,m-2).由
2.实数m取什么值时,复数z=2m+(4-m2)i在复平面内对应的点在:
(1)虚轴上;
(2)第一、三象限;
(3)以原点为圆心,4为半径的圆上.
【解析】(1)若复数z在复平面内的对应点位于虚轴上,
则2m=0,即m=0.
(2)若复数z在复平面内对应的点位于第一、三象限,
则2m(4-m2)>0,解得m<-2或0
则 =4,即m4-4m2=0,解得m=0或m=±2.
探究点二 复数与向量的一一对应
【典例2】1.已知A(1,2),B(-3,5),则向量 对应的复数为 ( )
A.1+2i B.-3+5i
C.-2+7i D.-4+3i
2.已知O为坐标原点,向量 对应的复数是4+3i,点A关于实轴的对称点为A1,
将向量 平移,使其起点移动到A点,这时终点为A2.
(1)求向量 对应的复数;
(2)求点A2对应的复数.
【思维导引】1.求出向量 的坐标,再确定对应的复数.
2.根据复数与点以及复数与向量的对应关系求解.
【解析】1.选D.由于A(1,2),B(-3,5),
则向量 =(-4,3),所以 对应的复数为-4+3i.
2.(1)因为向量 对应的复数是4+3i,
所以点A对应的复数也是4+3i,
因此点A坐标为(4,3),
所以点A关于实轴的对称点A1为(4,-3),
故向量 对应的复数是4-3i.
(2)依题意知 = ,而 =(4,-3),
设A2(x,y),则有(4,-3)=(x-4,y-3),
所以x=8,y=0,即A2(8,0).
所以点A2对应的复数是8.
【类题通法】
复数与向量的对应关系的两个关注点
(1)复数z=a+bi(a,b∈R)是与以原点为起点,Z(a,b)为终点的向量 一一对
应的.
(2)一个向量可以平移,其对应的复数不变,但是其起点与终点所对应的复数可
能改变.
提醒:向量是自由向量,其长度与方向与起点的位置无关, =(xB-xA,yB-yA),
对应的复数的实部和虚部分别是向量的横坐标和纵坐标.
【定向训练】
在复平面内,O为原点,向量 对应的复数为-1+2i,若点A关于直线y=-x的对
称点为点B,则向量 对应的复数为 ( )
A.-2-i B.-2+i
C.1+2i D.-1+2i
【解析】选B.因为复数-1+2i对应的点为A(-1,2),点A关于直线y=-x的对称点
为B(-2,1),
所以 对应的复数为-2+i.
【补偿训练】
已知平面直角坐标系中O是原点,向量 , 对应的复数分别为2-3i,-3+2i,
那么向量 对应的复数是________.?
【解析】向量 , 对应的复数分别为2-3i,-3+2i,根据复数与复平面内的
点一一对应,可得向量 =(2,-3), =(-3,2).
由向量减法的坐标运算可得向量 =(2+3,-3-2)=(5,-5),根据复数
与复平面内的点一一对应,可得向量 对应的复数是5-5i.
答案:5-5i
探究点三 共轭复数与复数的模
【典例3】1.已知复数z与复数z1=3-4i的模相等且与复数z2=a+5i互为共轭复数,则z= ( )
A.3+4i B.3-5i
C.5i D.-5i
2.已知z∈C,|z|=5,求z表示的点的轨迹.
【思维导引】1.两个共轭复数实部相等,虚部互为相反数,且二者的模相等.
2.设复数z对应向量 ,其中O为原点,根据圆的定义判断轨迹形状.
【解析】1.选D.因为复数z与复数z1=3-4i的模相等且与复数z2=a+5i互为共轭
复数,则|z|=|z1|=|z2|,得 = =5,所以a=0,z2=5i,z= =-5i.
2.设复数z对应向量 ,其中O为原点,根据|z|=5,得| |=5,由圆的定义,动
点Z的轨迹是以O为圆心,5为半径的圆,即复数z表示的点的轨迹是圆.
【类题通法】
关于复数的模的两个关注点
1.复数的模表示对应向量的长度,也就是对应的两点之间的距离.
2.注意复平面上两点间的距离公式的多角度应用:
设z1=a+bi,z2=c+di, =(a,b), =(c,d),
则 .
【定向训练】
1.已知复数z1=-2+i,z2=1-3i,对应的点分别为A,B,则向量| |=________.?
【解析】复数z1=-2+i,z2=1-3i,对应的点分别为A(-2,1),B(1,-3),
则向量 =(3,-4),所以| |=5.
答案:5
2.已知3-4i=x+yi(x,y∈R),则|1-5i|,|x-yi|,|y+2i|的大小关系为____________.?
【解析】由3-4i=x+yi(x,y∈R),
得x=3,y=-4.
而|1-5i|=
|x-yi|=|3+4i|= =5,
|y+2i|=|-4+2i|=
因为 <5< ,
所以|y+2i|<|x-yi|<|1-5i|.
答案:|y+2i|<|x-yi|<|1-5i|
【课堂小结】
课堂素养达标
1.在复平面内,复数z=4-5i对应的点的坐标为 ( )
A.(4,5) B.(4,-5)
C.(5,4) D.(-5,4)
【解析】选B.复数z=4-5i对应的点的坐标为(4,-5).
2.在复平面内,复数z=sin 2+icos 2对应的点位于 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【解析】选D.因为 <2<π,所以sin 2>0,cos 2<0.
故z=sin 2+icos 2对应的点在第四象限.
3.已知复数z满足|z|2-2|z|-3=0,则复数z对应点的轨迹为 ( )
A.一个圆 B.线段
C.两点 D.两个圆
【解析】选A.因为|z|2-2|z|-3=0,所以(|z|-3)(|z|+1)=0,所以|z|=3.故所求的轨迹为一个圆.
4.复平面内,点(0,-3)对应的复数为________.?
【解析】点(0,-3)对应的复数为-3i.
答案:-3i
