9.2正弦定理与余弦定理的应用 课件 2020-2021学年高一下学期数学人教B版(2019)必修第四册(47张PPT)
文档属性
| 名称 | 9.2正弦定理与余弦定理的应用 课件 2020-2021学年高一下学期数学人教B版(2019)必修第四册(47张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 822.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 00:00:00 | ||
图片预览








文档简介
9.2 正弦定理与余弦定理的应用
核心互动探究
探究点一 测量不可到达的两点之间的距离
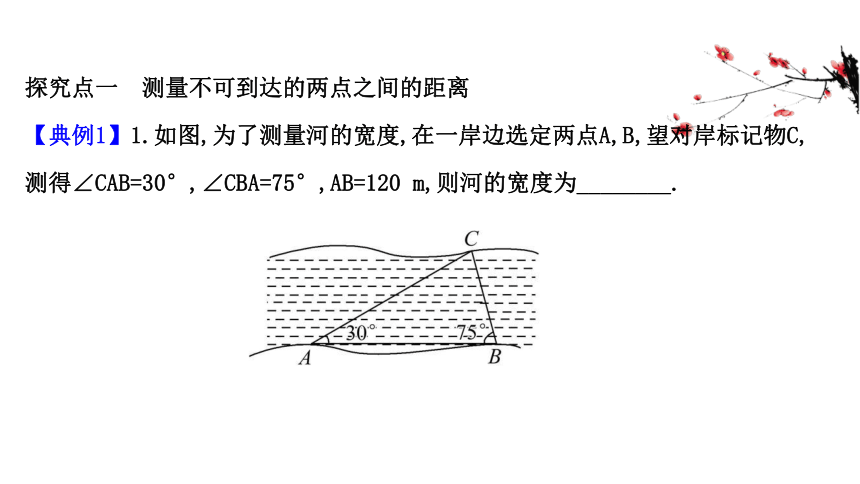
【典例1】1.如图,为了测量河的宽度,在一岸边选定两点A,B,望对岸标记物C,测得∠CAB=30°,∠CBA=75°,AB=120 m,则河的宽度为________.?
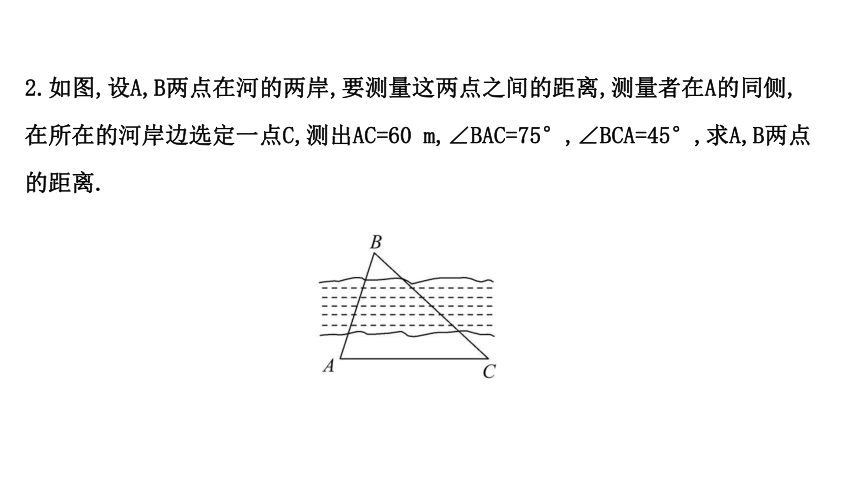
2.如图,设A,B两点在河的两岸,要测量这两点之间的距离,测量者在A的同侧,在所在的河岸边选定一点C,测出AC=60 m,∠BAC=75°,∠BCA=45°,求A,B两点的距离.
【思维导引】1.过点C作CD⊥AB,求CD即可.
2.在三角形中由正弦定理计算距离.
【解析】1.在△ABC中,过点C作CD⊥AB,因为AB=120 m,
∠CAB=30°,∠CBA=75°,所以∠ACB=180°-∠CAB-∠CBA=75°,
所以AC=AB=120 m,则河的宽度为CD=ACsin 30°=60 m.
答案:60 m
2.∠ABC=180°-75°-45°=60°,
所以由正弦定理得,
所以AB= (m).
即A,B两点间的距离为20 m.
【类题通法】
求距离问题时应注意的两点
(1)选定或确定所求量所在的三角形.若其他量已知,则直接解;若有未知量,则把未知量放在另一确定三角形中求解.
(2)确定用正弦定理还是余弦定理,如果都可用,就选择更便于计算的定理.
【定向训练】
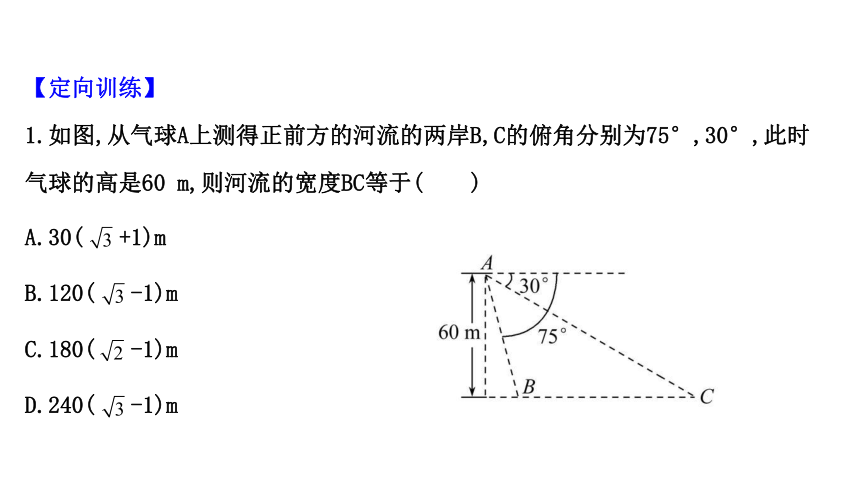
1.如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时
气球的高是60 m,则河流的宽度BC等于( )
A.30( +1)m
B.120( -1)m
C.180( -1)m
D.240( -1)m
【解题指南】记A点正下方为O,在△AOB与△AOC中,根据题中数据,分别求出OB,OC,则BC=OC-OB.
也可以先求出AB,再利用正弦定理计算BC.
【解析】选B.方法一:记A点正下方地面上对应的点为O,由题意可得OA=60 m,
∠ABO=75°,∠ACO=30°,在Rt△AOB中,由 =tan75°=tan(45°+30°)
=
得到OB= =60(2- )(m),
在Rt△AOC中,由 =tan30°=
得到OC= =60 (m),
所以河流的宽度BC=OC-OB=60 -60(2- )=120( -1)m.
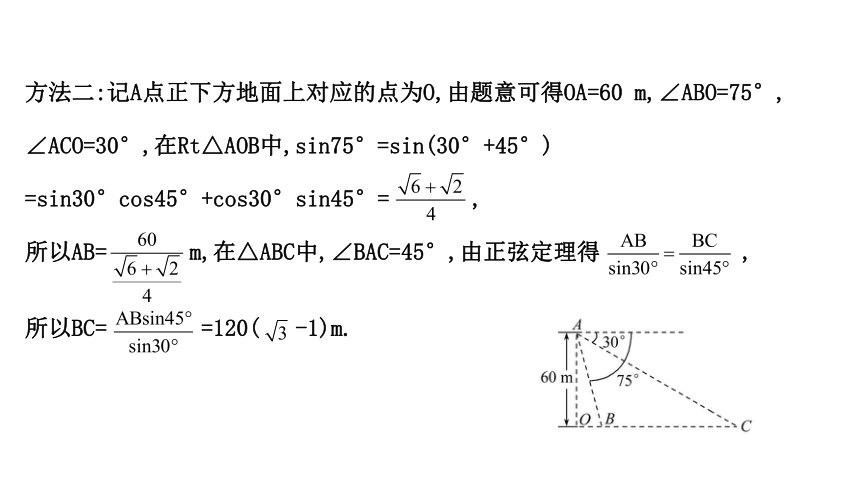
方法二:记A点正下方地面上对应的点为O,由题意可得OA=60 m,∠ABO=75°,
∠ACO=30°,在Rt△AOB中,sin75°=sin(30°+45°)
=sin30°cos45°+cos30°sin45°= ,
所以AB= m,在△ABC中,∠BAC=45°,由正弦定理得 ,
所以BC= =120( -1)m.
2.如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶,测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=0.1 km.试探究图中B,D间的距离与另外哪两点间的距离相等,然后求B,D间的距离(计算结果用根号表示).
【解题指南】先求∠ADC与∠BCD,进而可发现CB是△CAD底边AD的中垂线,所以BD=BA;而要求BD,可利用正弦定理在△ABC中求BA即可.
【解析】在△ADC中,∠DAC=30°,
∠ADC=60°-∠DAC=30°,所以CD=AC=0.1 km,
又因为∠BCD=180°-60°-60°=60°,
故CB是△CAD底边AD的中垂线,所以BD=BA,即B,D间的距离与另外B,A两点间的距离相等.
在△ABC中,
即AB= km,
因此BD= km,故B,D间的距离为 km.
探究点二 航行中的距离问题
【典例2】如图所示,为了测量A,B两处岛屿间的距离,小明在D处观测,A,B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,求A,B两处岛屿间的距离.
【思维导引】先在△ACD中求出AD,再在△DCB中求出BD,接着在△ABD中由余弦定理求得AB.
【解析】在△ACD中,∠ADC=15°+90°=105°,∠ACD=30°,
所以∠CAD=45°,
由正弦定理可得:
解得AD= (海里).
在Rt△DCB中,∠BDC=45°,
所以BD= CD=40 (海里).
在△ABD中,由余弦定理可得:
AB2=AD2+BD2-2AD·BDcos∠ADB
=800+3 200-2×20 ×40 × =2 400,
解得AB=20 (海里).
答:A,B两处岛屿间的距离为20 海里.
【类题通法】
航行问题的解题技巧
(1)在航行等问题中,通常是把方位角(方向角)与几何图形结合起来,求出几何图形的有关角.
(2)几何图形的应用是解决实际问题的重要辅助手段,一是从图形的完整性方面画出图形;二是把多边形向三角形转化.
【定向训练】
一艘海轮从A出发,沿北偏东80°的方向航行6 n mile后到达海岛B,然后从B出发,沿北偏东20°的方向航行6 n mile后到达海岛C.如果直接从A出发到达C,此船应该沿怎样的方向航行,需要航行多少距离?
【解题指南】要求航行方向及航行距离,只要在△ABC中求出∠BAC以及AC即可.
【解析】在△ABC中,AB=BC=6 n mile,
∠ABC=180°-80°+20°=120°,
所以∠BAC=∠BCA=30°,
由余弦定理得AC=
又∠BAC=30°,所以80°-∠BAC=50°.
答:此船应该沿北偏东50°的方向航行,需要航行6 n mile.
【补偿训练】
如图所示,某观测站C在城A的南偏西20°的方向,从城A出发有一条走向为南偏东40°的公路,在C处观测到距离C 31 km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20 km后到达D处,测得C,D两处的距离为21 km,这时此车距离A城多少千米?
【解析】在△BCD中,BC=31 km,
BD=20 km,CD=21 km,
由余弦定理得cos∠BDC=
所以cos∠ADC= ,
所以sin∠ADC=
在△ACD中,由条件知CD=21 km,
∠BAC=20°+40°=60°,
所以sin∠ACD=sin(60°+∠ADC)=
由正弦定理得
所以AD= =15(km).
故这时此车距离A城15 km.
探究点三 高度、角度问题
【典例3】1.如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600 m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=________m.?
2.如图,已知两条公路AB,AC的交汇点A处有一学校,现拟在两条公路之间的区
域内建一工厂P,在两公路旁M,N(异于点A)处设两个销售点,且满足∠A=∠PMN=75°,MN=( + )千米,PM=2 千米,设∠AMN=θ.
(1)试用θ表示AM,并写出θ的范围;
(2)当θ为多大时,工厂产生的噪声对学校的影响最小(即工厂与学校的距离最
远).(注:sin 75°= )
【思维导引】1.将空间几何问题转化为平面几何问题,解三角形.
2.(1)利用正弦定理解决;
(2)由余弦定理转化为求三角函数的最小值.
【解析】1.如图所示,由已知得∠BAC=30°,AB=600 m,∠EBC=75°,∠CBD=30°,
在△ABC中,∠ACB=∠EBC-∠BAC=45°,
由 得BC= =300 (m).
在Rt△BCD中,CD=BC·tan ∠CBD=300 × =100 (m).
答案:100
2.(1)因为∠AMN=θ,在△AMN中,
由正弦定理得
因为MN= ,所以AM=4sin(75°+θ)(0°<θ<105°).
(2)连接AP,在△APM中,AM=4sin(75°+θ),
所以由余弦定理得AP2=AM2+MP2-2AM·MPcos∠AMP
=16sin2(75°+θ)+12-16 ·sin(75°+θ)cos(75°+θ)
=8[1-cos(2θ+150°)]-8 sin(2θ+150°)+12
=20-8[ sin(2θ+150°)+cos(2θ+150°)]
=20-16sin(2θ+180°)
=20+16sin2θ(0°<θ<105°),
当且仅当2θ=90°,即θ=45°时,AP2取得最大值36,即AP取得最大值6.
所以当θ=45°时,工厂产生的噪声对学校的影响最小.
【类题通法】
计算高度的注意事项
(1)解决有关高度问题时,正确理解仰角、俯角是关键.
(2)在实际问题中,当研究空间与平面(地面)的问题时,通常画两个图形,一个
空间图形,一个平面图形,把空间问题转化为平面问题,明确三角形中的边长和
角度,确定应用正弦定理或余弦定理计算.
提醒:
【定向训练】
1.如图,在山脚A测得山顶P的仰角为30°,沿倾斜角为15°的斜坡向上走a米到
B,在B处测得山顶P的仰角为60°,则山高PQ= ( )
A.a米 B. 米 C. a米 D. a米
【解题指南】设∠QAP=α=30°,∠QAB=β=15°,∠CBP=γ=60°,在△PAB中,
∠PAB=α-β=15°,∠BPA= =γ-α=30°,
由正弦定理可求PB,根据PQ=PC+CQ=PB·sin γ+asin β可得结果.
【解析】选C.设∠QAP=α=30°,∠QAB=β=15°,∠CBP=γ=60°,
在△PAB中,∠PAB=α-β=15°, ∠BPA= =γ-α=30°,
由正弦定理得 ,所以PB= a.
所以PQ=PC+CQ=PB·sin γ+asin β
= a×sin 60°+asin 15°= a(米).
2.某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/时的航行速度向正东方向匀速行驶,经过t小时小艇与轮船相遇.假设小艇的最高航行速度只能达到30海里/时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短的时间与轮船相遇,并说明理由.
【解题指南】先画出简图,再对照图形理解题意,然后确定各个角度、各条边长(边长有已知的,有用字母表示的),并尝试用正、余弦定理,函数,不等式的知识解答.
【解析】设小艇航行速度的大小是v海里/时,
如图所示,设小艇与轮船在B处相遇.
由余弦定理得:
BO2=AO2+AB2-2AO·ABcos A.
所以(vt)2=400+(30t)2-2×20×30tcos (90°-30°),
即(v2-900)t2+600t-400=0(其中0①当0=1 600(v2-675),令Δ=0,
即1 600(v2-675)=0,
则v=15 ,
1°当02°当15 ≤v<30时,
当 时,
令x= 则x∈[0,15),
当且仅当x=0,即v=15 时,等号成立;
当 时,同理可得所以当15 ≤v<30时,t> ;
②当v=30时,可求得t= ;
综合①②可知,当v=30时,t取得最小值,且最小值是 ,
此时,在△OAB中,有OA=OB=AB=20,所以可设计方案如下:
小艇的航行方向是北偏东30°,航行速度为30海里/时,此时小艇能以最短的时
间与轮船相遇.
【课堂小结】
课堂素养达标
1.为测一河两岸相对两电线杆A,B间的距离,在距A点12米的C处(AC⊥AB)测得
∠ACB=30°,则A,B间的距离应为 ( )
A.6米 B.4 米 C.6 米 D.12 米
【解析】选B.在△ABC中,A=90°, ∠ACB=30°,
由tan 30°= ,得AB=ACtan30°=4 (米).
2.在某次测量中,A在B的北偏东55°,则B在A的 ( )
A.北偏西35° B.北偏东55°
C.北偏东35° D.南偏西55°
【解析】选D.根据题意和方向角的概念画出示意图,如图所示.α=55°,
则β=α=55°,所以B在A的南偏西55°.
3.如图,要测出山上信号发射塔BC的高,从山脚A测得AC=30 m,塔顶B的仰角为45°,塔底C的仰角为15°,则信号发射塔BC的高为 ( )
A.15 m B.15 m C.30 m D.30 m
【解析】选B.由题意可知,AC=30 m,∠BAD=45°,∠CAD=15°,得∠B=45°,
∠BAC=30°,由正弦定理可知, 解得BC=15 m.
4.一轮船向正北方向航行,某时刻在A处测得灯塔M在正西方向且相距20 海
里,另一灯塔N在北偏东30°方向,继续航行20海里至B处时,测得灯塔N在南偏
东60°方向,则两灯塔之间的距离是________海里.?
【解析】由已知得AM=20 海里,AB=20海里,∠BAN=30°,∠ABN=60°,
所以∠ANB=90°,AN=20× =10 (海里).而∠MAN=120°,故
MN2=1 200+300-2×20 ×10 × ,所以MN=10 海里.
答案:10
核心互动探究
探究点一 测量不可到达的两点之间的距离
【典例1】1.如图,为了测量河的宽度,在一岸边选定两点A,B,望对岸标记物C,测得∠CAB=30°,∠CBA=75°,AB=120 m,则河的宽度为________.?
2.如图,设A,B两点在河的两岸,要测量这两点之间的距离,测量者在A的同侧,在所在的河岸边选定一点C,测出AC=60 m,∠BAC=75°,∠BCA=45°,求A,B两点的距离.
【思维导引】1.过点C作CD⊥AB,求CD即可.
2.在三角形中由正弦定理计算距离.
【解析】1.在△ABC中,过点C作CD⊥AB,因为AB=120 m,
∠CAB=30°,∠CBA=75°,所以∠ACB=180°-∠CAB-∠CBA=75°,
所以AC=AB=120 m,则河的宽度为CD=ACsin 30°=60 m.
答案:60 m
2.∠ABC=180°-75°-45°=60°,
所以由正弦定理得,
所以AB= (m).
即A,B两点间的距离为20 m.
【类题通法】
求距离问题时应注意的两点
(1)选定或确定所求量所在的三角形.若其他量已知,则直接解;若有未知量,则把未知量放在另一确定三角形中求解.
(2)确定用正弦定理还是余弦定理,如果都可用,就选择更便于计算的定理.
【定向训练】
1.如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时
气球的高是60 m,则河流的宽度BC等于( )
A.30( +1)m
B.120( -1)m
C.180( -1)m
D.240( -1)m
【解题指南】记A点正下方为O,在△AOB与△AOC中,根据题中数据,分别求出OB,OC,则BC=OC-OB.
也可以先求出AB,再利用正弦定理计算BC.
【解析】选B.方法一:记A点正下方地面上对应的点为O,由题意可得OA=60 m,
∠ABO=75°,∠ACO=30°,在Rt△AOB中,由 =tan75°=tan(45°+30°)
=
得到OB= =60(2- )(m),
在Rt△AOC中,由 =tan30°=
得到OC= =60 (m),
所以河流的宽度BC=OC-OB=60 -60(2- )=120( -1)m.
方法二:记A点正下方地面上对应的点为O,由题意可得OA=60 m,∠ABO=75°,
∠ACO=30°,在Rt△AOB中,sin75°=sin(30°+45°)
=sin30°cos45°+cos30°sin45°= ,
所以AB= m,在△ABC中,∠BAC=45°,由正弦定理得 ,
所以BC= =120( -1)m.
2.如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶,测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=0.1 km.试探究图中B,D间的距离与另外哪两点间的距离相等,然后求B,D间的距离(计算结果用根号表示).
【解题指南】先求∠ADC与∠BCD,进而可发现CB是△CAD底边AD的中垂线,所以BD=BA;而要求BD,可利用正弦定理在△ABC中求BA即可.
【解析】在△ADC中,∠DAC=30°,
∠ADC=60°-∠DAC=30°,所以CD=AC=0.1 km,
又因为∠BCD=180°-60°-60°=60°,
故CB是△CAD底边AD的中垂线,所以BD=BA,即B,D间的距离与另外B,A两点间的距离相等.
在△ABC中,
即AB= km,
因此BD= km,故B,D间的距离为 km.
探究点二 航行中的距离问题
【典例2】如图所示,为了测量A,B两处岛屿间的距离,小明在D处观测,A,B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,求A,B两处岛屿间的距离.
【思维导引】先在△ACD中求出AD,再在△DCB中求出BD,接着在△ABD中由余弦定理求得AB.
【解析】在△ACD中,∠ADC=15°+90°=105°,∠ACD=30°,
所以∠CAD=45°,
由正弦定理可得:
解得AD= (海里).
在Rt△DCB中,∠BDC=45°,
所以BD= CD=40 (海里).
在△ABD中,由余弦定理可得:
AB2=AD2+BD2-2AD·BDcos∠ADB
=800+3 200-2×20 ×40 × =2 400,
解得AB=20 (海里).
答:A,B两处岛屿间的距离为20 海里.
【类题通法】
航行问题的解题技巧
(1)在航行等问题中,通常是把方位角(方向角)与几何图形结合起来,求出几何图形的有关角.
(2)几何图形的应用是解决实际问题的重要辅助手段,一是从图形的完整性方面画出图形;二是把多边形向三角形转化.
【定向训练】
一艘海轮从A出发,沿北偏东80°的方向航行6 n mile后到达海岛B,然后从B出发,沿北偏东20°的方向航行6 n mile后到达海岛C.如果直接从A出发到达C,此船应该沿怎样的方向航行,需要航行多少距离?
【解题指南】要求航行方向及航行距离,只要在△ABC中求出∠BAC以及AC即可.
【解析】在△ABC中,AB=BC=6 n mile,
∠ABC=180°-80°+20°=120°,
所以∠BAC=∠BCA=30°,
由余弦定理得AC=
又∠BAC=30°,所以80°-∠BAC=50°.
答:此船应该沿北偏东50°的方向航行,需要航行6 n mile.
【补偿训练】
如图所示,某观测站C在城A的南偏西20°的方向,从城A出发有一条走向为南偏东40°的公路,在C处观测到距离C 31 km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20 km后到达D处,测得C,D两处的距离为21 km,这时此车距离A城多少千米?
【解析】在△BCD中,BC=31 km,
BD=20 km,CD=21 km,
由余弦定理得cos∠BDC=
所以cos∠ADC= ,
所以sin∠ADC=
在△ACD中,由条件知CD=21 km,
∠BAC=20°+40°=60°,
所以sin∠ACD=sin(60°+∠ADC)=
由正弦定理得
所以AD= =15(km).
故这时此车距离A城15 km.
探究点三 高度、角度问题
【典例3】1.如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600 m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=________m.?
2.如图,已知两条公路AB,AC的交汇点A处有一学校,现拟在两条公路之间的区
域内建一工厂P,在两公路旁M,N(异于点A)处设两个销售点,且满足∠A=∠PMN=75°,MN=( + )千米,PM=2 千米,设∠AMN=θ.
(1)试用θ表示AM,并写出θ的范围;
(2)当θ为多大时,工厂产生的噪声对学校的影响最小(即工厂与学校的距离最
远).(注:sin 75°= )
【思维导引】1.将空间几何问题转化为平面几何问题,解三角形.
2.(1)利用正弦定理解决;
(2)由余弦定理转化为求三角函数的最小值.
【解析】1.如图所示,由已知得∠BAC=30°,AB=600 m,∠EBC=75°,∠CBD=30°,
在△ABC中,∠ACB=∠EBC-∠BAC=45°,
由 得BC= =300 (m).
在Rt△BCD中,CD=BC·tan ∠CBD=300 × =100 (m).
答案:100
2.(1)因为∠AMN=θ,在△AMN中,
由正弦定理得
因为MN= ,所以AM=4sin(75°+θ)(0°<θ<105°).
(2)连接AP,在△APM中,AM=4sin(75°+θ),
所以由余弦定理得AP2=AM2+MP2-2AM·MPcos∠AMP
=16sin2(75°+θ)+12-16 ·sin(75°+θ)cos(75°+θ)
=8[1-cos(2θ+150°)]-8 sin(2θ+150°)+12
=20-8[ sin(2θ+150°)+cos(2θ+150°)]
=20-16sin(2θ+180°)
=20+16sin2θ(0°<θ<105°),
当且仅当2θ=90°,即θ=45°时,AP2取得最大值36,即AP取得最大值6.
所以当θ=45°时,工厂产生的噪声对学校的影响最小.
【类题通法】
计算高度的注意事项
(1)解决有关高度问题时,正确理解仰角、俯角是关键.
(2)在实际问题中,当研究空间与平面(地面)的问题时,通常画两个图形,一个
空间图形,一个平面图形,把空间问题转化为平面问题,明确三角形中的边长和
角度,确定应用正弦定理或余弦定理计算.
提醒:
【定向训练】
1.如图,在山脚A测得山顶P的仰角为30°,沿倾斜角为15°的斜坡向上走a米到
B,在B处测得山顶P的仰角为60°,则山高PQ= ( )
A.a米 B. 米 C. a米 D. a米
【解题指南】设∠QAP=α=30°,∠QAB=β=15°,∠CBP=γ=60°,在△PAB中,
∠PAB=α-β=15°,∠BPA= =γ-α=30°,
由正弦定理可求PB,根据PQ=PC+CQ=PB·sin γ+asin β可得结果.
【解析】选C.设∠QAP=α=30°,∠QAB=β=15°,∠CBP=γ=60°,
在△PAB中,∠PAB=α-β=15°, ∠BPA= =γ-α=30°,
由正弦定理得 ,所以PB= a.
所以PQ=PC+CQ=PB·sin γ+asin β
= a×sin 60°+asin 15°= a(米).
2.某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/时的航行速度向正东方向匀速行驶,经过t小时小艇与轮船相遇.假设小艇的最高航行速度只能达到30海里/时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短的时间与轮船相遇,并说明理由.
【解题指南】先画出简图,再对照图形理解题意,然后确定各个角度、各条边长(边长有已知的,有用字母表示的),并尝试用正、余弦定理,函数,不等式的知识解答.
【解析】设小艇航行速度的大小是v海里/时,
如图所示,设小艇与轮船在B处相遇.
由余弦定理得:
BO2=AO2+AB2-2AO·ABcos A.
所以(vt)2=400+(30t)2-2×20×30tcos (90°-30°),
即(v2-900)t2+600t-400=0(其中0
即1 600(v2-675)=0,
则v=15 ,
1°当0
当 时,
令x= 则x∈[0,15),
当且仅当x=0,即v=15 时,等号成立;
当 时,同理可得
②当v=30时,可求得t= ;
综合①②可知,当v=30时,t取得最小值,且最小值是 ,
此时,在△OAB中,有OA=OB=AB=20,所以可设计方案如下:
小艇的航行方向是北偏东30°,航行速度为30海里/时,此时小艇能以最短的时
间与轮船相遇.
【课堂小结】
课堂素养达标
1.为测一河两岸相对两电线杆A,B间的距离,在距A点12米的C处(AC⊥AB)测得
∠ACB=30°,则A,B间的距离应为 ( )
A.6米 B.4 米 C.6 米 D.12 米
【解析】选B.在△ABC中,A=90°, ∠ACB=30°,
由tan 30°= ,得AB=ACtan30°=4 (米).
2.在某次测量中,A在B的北偏东55°,则B在A的 ( )
A.北偏西35° B.北偏东55°
C.北偏东35° D.南偏西55°
【解析】选D.根据题意和方向角的概念画出示意图,如图所示.α=55°,
则β=α=55°,所以B在A的南偏西55°.
3.如图,要测出山上信号发射塔BC的高,从山脚A测得AC=30 m,塔顶B的仰角为45°,塔底C的仰角为15°,则信号发射塔BC的高为 ( )
A.15 m B.15 m C.30 m D.30 m
【解析】选B.由题意可知,AC=30 m,∠BAD=45°,∠CAD=15°,得∠B=45°,
∠BAC=30°,由正弦定理可知, 解得BC=15 m.
4.一轮船向正北方向航行,某时刻在A处测得灯塔M在正西方向且相距20 海
里,另一灯塔N在北偏东30°方向,继续航行20海里至B处时,测得灯塔N在南偏
东60°方向,则两灯塔之间的距离是________海里.?
【解析】由已知得AM=20 海里,AB=20海里,∠BAN=30°,∠ABN=60°,
所以∠ANB=90°,AN=20× =10 (海里).而∠MAN=120°,故
MN2=1 200+300-2×20 ×10 × ,所以MN=10 海里.
答案:10
