江西省师大附中2012届高三下学期开学考试(数学理)
文档属性
| 名称 | 江西省师大附中2012届高三下学期开学考试(数学理) |
|
|
| 格式 | zip | ||
| 文件大小 | 184.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-06 00:00:00 | ||
图片预览





文档简介
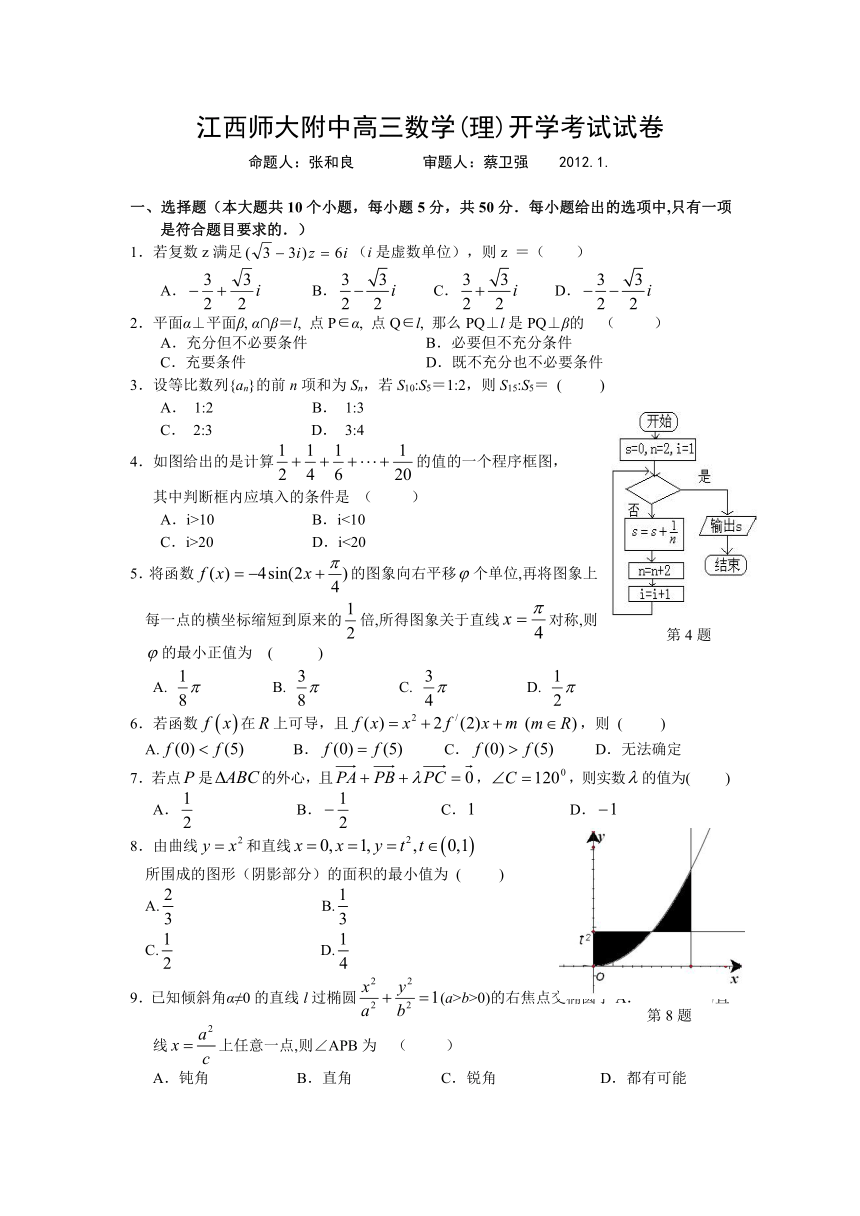
江西师大附中高三数学(理)开学考试试卷
命题人:张和良 审题人:蔡卫强 2012.1.
一、选择题(本大题共10个小题,每小题5分,共50分.每小题给出的选项中,只有一项是符合题目要求的.)
1.若复数z满足(i是虚数单位),则z =( )
A. B. C. D.
2.平面α⊥平面β, α∩β=l, 点P∈α, 点Q∈l, 那么PQ⊥l是PQ⊥β的 ( )
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分也不必要条件
3.设等比数列{an}的前n项和为Sn,若S10:S5=1:2,则S15:S5= ( )
A. 1:2 B. 1:3
C. 2:3 D. 3:4
4.如图给出的是计算的值的一个程序框图,
其中判断框内应填入的条件是 ( )
A.i>10 B.i<10
C.i>20 D.i<20
5.将函数的图象向右平移个单位,再将图象上每一点的横坐标缩短到原来的倍,所得图象关于直线对称,则的最小正值为 ( )
A. B. C. D.
6.若函数在上可导,且,则 ( )
A. B. C. D.无法确定
7.若点是的外心,且,,则实数的值为( )
A. B. C. D.
8.由曲线和直线
所围成的图形(阴影部分)的面积的最小值为 ( )
A. B.
C. D.
9.已知倾斜角α≠0的直线l过椭圆(a>b>0)的右焦点交椭圆于A.B两点,P为直线上任意一点,则∠APB为 ( )
A.钝角 B.直角 C.锐角 D.都有可能
10.已知,实数、、满足 ,(0<<<)若实数是函数y=的一个零点,那么下列不等式中,不可能成立的是( )
A. B. C. D.
二、填空题(本大题共5个小题,每小题5分,共25分.)
11.设,则的最小值为 .
12.已知变量满足约束条件,若目标函数(其中)仅在点处取得最大值,则的取值范围是 .
13.一个几何体的三视图如右图所示,其中正视图和侧视图是腰长为6的两个全等的等腰直角三角形.则它的体积为 .
14.对于定义在R上的函数f(x),有下述命题:
①若f(x)为奇函数,则的图象关于点A(1,0)对称;
②若对x∈R,有=,则f(x)的图象关于直线x=1对称;
③若函数的图象关于直线x=1对称,则f(x)为偶函数;
④函数与函数的图象关于直线x=1对称.
其中正确命题的序号是______________.
15.(不等式选做题)
若不等式,对满足的一切实数恒成立,则实数的取值范围是 .
三、解答题(本大题共6小题,共75分,解答应写出文字说明.证明过程或演算步骤.)
16.(本题满分12分)已知点P到两个定点M(-1,0)、N(1,0)距离的比为,点N到直线PM的距离为1,求直线PN的方程.
17.(本题满分12分)设、、分别是△ABC三个内角A、B、C的对边,若向量,且 .
(Ⅰ)求的值;
(Ⅱ)求的最大值.
18.(本题满分12分)已知斜三棱柱的底面是直角三角形,,侧棱与底面所成角为,点在底面上射影D落在BC上.
(Ⅰ)求证:平面;
(Ⅱ)若点D恰为BC中点,且,求的大小;
(III)若,且当时,求二面角的大小.
19.(本题满分12分)已知平面上一定点C(4,0)和一定直线为该平面上一动点,作,垂足为Q,且(
(Ⅰ)问点P在什么曲线上?并求出该曲线的方程;
(Ⅱ)设直线与(1)中的曲线交于不同的两点A、B,是否存在实数k,使 得以线段AB为直径的圆经过点D(0,-2)?若存在,求出k的值,若不存在,说明理由
20.(本题满分13分)已知函数,
(Ⅰ)若函数在上是减函数,求实数的取值范围;
(Ⅱ)令,是否存在实数,当(是自然常数)时,函数的最小值是3,若存在,求出的值;若不存在,说明理由;
(III)当时,证明:
21.(本题满分14分)在数列中,,其中.
(Ⅰ)求数列的通项公式;
(Ⅱ)求数列的前项和;
(Ⅲ)证明存在,使得对任意均成立.
江西师大附中高三(理)数学答案2012.1.30
一、选择题 ACDAB CDDCD
二、填空题 11.8 12.(1,+∞) 13.72 14.①③ 15.
三、解答题
16.(本题满分12分)已知点P到两个定点M(-1,0)、N(1,0)距离的比为,点N到直线PM的距离为1,求直线PN的方程.
解:设点P的坐标为(x,y),由题设有, 即.
整理得 x2+y2-6x+1=0. ①
因为点N到PM的距离为1,|MN|=2,所以∠PMN=30°,直线PM的斜率为±,
直线PM的方程为y=±(x+1). ②
将②式代入①式整理得x2-4x+1=0.解得x=2+,x=2-.
代入②式得点P的坐标为(2+,1+)或(2-,-1+);
(2+,-1-)或(2-,1-).∴直线PN的方程为y=x-1或y=-x+1.
17.(本题满分12分)设、、分别是△ABC三个内角A、B、C的对边,若向量 ,且.
(Ⅰ)求的值;
(Ⅱ)求的最大值.
解:(Ⅰ) 由,得
即 , 亦即
所以
(Ⅱ) 因,
而, 所以,有最小值.
当时,取得最小值. 又,则有最大值.
故的最大值为.
18.(本题满分12分)已知斜三棱柱的底面是直角三角形,,侧棱与底面所成角为,点在底面上射影D落在BC上.
(Ⅰ)求证:平面;
(Ⅱ)若点D恰为BC中点,且,求的大小;
(III)若,且当时,求二面角的大小.
解:(I)∵B1D⊥平面ABC,AC平面ABC,∴
又∵,,∴AC⊥平面
(II)
∴四边形为菱形, 又∵D为BC的中点,
∴为侧棱和底面所成的角,∴
∴,即侧棱与底面所成角.
(III)以C为原点,CA为x轴CB为y轴,过C点且垂直于平面ABC的直线为Z轴,建立空间直角坐标系,
则A(a,0,0),B(0,a,0),,平面ABC的法向量,设平面ABC1的法向量为,
由,即, ,
∵二面角大小是锐二面角, ∴二面角的大小是.
19.(本题满分12分)已知平面上一定点C(4,0)和一定直线为该平面上一动点,作,垂足为Q,且(
(Ⅰ)问点P在什么曲线上?并求出该曲线的方程;
(Ⅱ)设直线与(1)中的曲线交于不同的两点A、B,是否存在实数k,使 得以线段AB为直径的圆经过点D(0,-2)?若存在,求出k的值,若不存在,说明理由 ( http: / / www. / )
解:(Ⅰ)设P的坐标为,由 得
∴(化简得 ∴P点在双曲线上,其方程为
(Ⅱ)设A、B点的坐标分别为、,由 得
, ∵AB与双曲线交于两点,∴△>0,
即 解得
∵若以AB为直径的圆过D(0,-2),则AD⊥BD, ∴,即
∴ ∴
∴, 即存在符合要求.
20.(本题满分13分)已知函数,
(Ⅰ)若函数在上是减函数,求实数的取值范围;
(Ⅱ)令,是否存在实数,当(是自然常数)时,函数的最小值是3,若存在,求出的值;若不存在,说明理由;
(III)当时,证明:
解:(Ⅰ)在上恒成立,
令 ,有 得 得 .
(Ⅱ)假设存在实数,使()有最小值3,
①当时,在上单调递减,,(舍去),
②当时,在上单调递减,在上单调递增
,,满足条件.
③当时,在上单调递减,,(舍去),
综上,存在实数,使得当时有最小值3.
(III)令,由(2)知,.令,,
当时,,在上单调递增
∴ 即
21.(本题满分14分)在数列中,,其中.
(Ⅰ)求数列的通项公式;
(Ⅱ)求数列的前项和;
(Ⅲ)证明存在,使得对任意均成立.
解:(Ⅰ)解法一:, ,
.由此可猜想出数列的通项公式为.
以下用数学归纳法证明.
(1)当时,,等式成立.
(2)假设当时等式成立,即,
那么.
这就是说,当时等式也成立.根据(1)和(2)可知,等式对任何都成立.
解法二:由,,可得,
所以为等差数列,其公差为1,首项为0,故,所以数列的通项公式为.
(Ⅱ)解:设, ①
②
当时,①式减去②式,
得,
.
这时数列的前项和.
当时,.这时数列的前项和.
(Ⅲ)证明:通过分析,推测数列的第一项最大,下面证明:
. ③
由知,要使③式成立,只要,
因为
.
所以③式成立.
因此,存在,使得对任意均成立.
第4题
第8题
正视图
侧视图
俯视图
命题人:张和良 审题人:蔡卫强 2012.1.
一、选择题(本大题共10个小题,每小题5分,共50分.每小题给出的选项中,只有一项是符合题目要求的.)
1.若复数z满足(i是虚数单位),则z =( )
A. B. C. D.
2.平面α⊥平面β, α∩β=l, 点P∈α, 点Q∈l, 那么PQ⊥l是PQ⊥β的 ( )
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分也不必要条件
3.设等比数列{an}的前n项和为Sn,若S10:S5=1:2,则S15:S5= ( )
A. 1:2 B. 1:3
C. 2:3 D. 3:4
4.如图给出的是计算的值的一个程序框图,
其中判断框内应填入的条件是 ( )
A.i>10 B.i<10
C.i>20 D.i<20
5.将函数的图象向右平移个单位,再将图象上每一点的横坐标缩短到原来的倍,所得图象关于直线对称,则的最小正值为 ( )
A. B. C. D.
6.若函数在上可导,且,则 ( )
A. B. C. D.无法确定
7.若点是的外心,且,,则实数的值为( )
A. B. C. D.
8.由曲线和直线
所围成的图形(阴影部分)的面积的最小值为 ( )
A. B.
C. D.
9.已知倾斜角α≠0的直线l过椭圆(a>b>0)的右焦点交椭圆于A.B两点,P为直线上任意一点,则∠APB为 ( )
A.钝角 B.直角 C.锐角 D.都有可能
10.已知,实数、、满足 ,(0<<<)若实数是函数y=的一个零点,那么下列不等式中,不可能成立的是( )
A. B. C. D.
二、填空题(本大题共5个小题,每小题5分,共25分.)
11.设,则的最小值为 .
12.已知变量满足约束条件,若目标函数(其中)仅在点处取得最大值,则的取值范围是 .
13.一个几何体的三视图如右图所示,其中正视图和侧视图是腰长为6的两个全等的等腰直角三角形.则它的体积为 .
14.对于定义在R上的函数f(x),有下述命题:
①若f(x)为奇函数,则的图象关于点A(1,0)对称;
②若对x∈R,有=,则f(x)的图象关于直线x=1对称;
③若函数的图象关于直线x=1对称,则f(x)为偶函数;
④函数与函数的图象关于直线x=1对称.
其中正确命题的序号是______________.
15.(不等式选做题)
若不等式,对满足的一切实数恒成立,则实数的取值范围是 .
三、解答题(本大题共6小题,共75分,解答应写出文字说明.证明过程或演算步骤.)
16.(本题满分12分)已知点P到两个定点M(-1,0)、N(1,0)距离的比为,点N到直线PM的距离为1,求直线PN的方程.
17.(本题满分12分)设、、分别是△ABC三个内角A、B、C的对边,若向量,且 .
(Ⅰ)求的值;
(Ⅱ)求的最大值.
18.(本题满分12分)已知斜三棱柱的底面是直角三角形,,侧棱与底面所成角为,点在底面上射影D落在BC上.
(Ⅰ)求证:平面;
(Ⅱ)若点D恰为BC中点,且,求的大小;
(III)若,且当时,求二面角的大小.
19.(本题满分12分)已知平面上一定点C(4,0)和一定直线为该平面上一动点,作,垂足为Q,且(
(Ⅰ)问点P在什么曲线上?并求出该曲线的方程;
(Ⅱ)设直线与(1)中的曲线交于不同的两点A、B,是否存在实数k,使 得以线段AB为直径的圆经过点D(0,-2)?若存在,求出k的值,若不存在,说明理由
20.(本题满分13分)已知函数,
(Ⅰ)若函数在上是减函数,求实数的取值范围;
(Ⅱ)令,是否存在实数,当(是自然常数)时,函数的最小值是3,若存在,求出的值;若不存在,说明理由;
(III)当时,证明:
21.(本题满分14分)在数列中,,其中.
(Ⅰ)求数列的通项公式;
(Ⅱ)求数列的前项和;
(Ⅲ)证明存在,使得对任意均成立.
江西师大附中高三(理)数学答案2012.1.30
一、选择题 ACDAB CDDCD
二、填空题 11.8 12.(1,+∞) 13.72 14.①③ 15.
三、解答题
16.(本题满分12分)已知点P到两个定点M(-1,0)、N(1,0)距离的比为,点N到直线PM的距离为1,求直线PN的方程.
解:设点P的坐标为(x,y),由题设有, 即.
整理得 x2+y2-6x+1=0. ①
因为点N到PM的距离为1,|MN|=2,所以∠PMN=30°,直线PM的斜率为±,
直线PM的方程为y=±(x+1). ②
将②式代入①式整理得x2-4x+1=0.解得x=2+,x=2-.
代入②式得点P的坐标为(2+,1+)或(2-,-1+);
(2+,-1-)或(2-,1-).∴直线PN的方程为y=x-1或y=-x+1.
17.(本题满分12分)设、、分别是△ABC三个内角A、B、C的对边,若向量 ,且.
(Ⅰ)求的值;
(Ⅱ)求的最大值.
解:(Ⅰ) 由,得
即 , 亦即
所以
(Ⅱ) 因,
而, 所以,有最小值.
当时,取得最小值. 又,则有最大值.
故的最大值为.
18.(本题满分12分)已知斜三棱柱的底面是直角三角形,,侧棱与底面所成角为,点在底面上射影D落在BC上.
(Ⅰ)求证:平面;
(Ⅱ)若点D恰为BC中点,且,求的大小;
(III)若,且当时,求二面角的大小.
解:(I)∵B1D⊥平面ABC,AC平面ABC,∴
又∵,,∴AC⊥平面
(II)
∴四边形为菱形, 又∵D为BC的中点,
∴为侧棱和底面所成的角,∴
∴,即侧棱与底面所成角.
(III)以C为原点,CA为x轴CB为y轴,过C点且垂直于平面ABC的直线为Z轴,建立空间直角坐标系,
则A(a,0,0),B(0,a,0),,平面ABC的法向量,设平面ABC1的法向量为,
由,即, ,
∵二面角大小是锐二面角, ∴二面角的大小是.
19.(本题满分12分)已知平面上一定点C(4,0)和一定直线为该平面上一动点,作,垂足为Q,且(
(Ⅰ)问点P在什么曲线上?并求出该曲线的方程;
(Ⅱ)设直线与(1)中的曲线交于不同的两点A、B,是否存在实数k,使 得以线段AB为直径的圆经过点D(0,-2)?若存在,求出k的值,若不存在,说明理由 ( http: / / www. / )
解:(Ⅰ)设P的坐标为,由 得
∴(化简得 ∴P点在双曲线上,其方程为
(Ⅱ)设A、B点的坐标分别为、,由 得
, ∵AB与双曲线交于两点,∴△>0,
即 解得
∵若以AB为直径的圆过D(0,-2),则AD⊥BD, ∴,即
∴ ∴
∴, 即存在符合要求.
20.(本题满分13分)已知函数,
(Ⅰ)若函数在上是减函数,求实数的取值范围;
(Ⅱ)令,是否存在实数,当(是自然常数)时,函数的最小值是3,若存在,求出的值;若不存在,说明理由;
(III)当时,证明:
解:(Ⅰ)在上恒成立,
令 ,有 得 得 .
(Ⅱ)假设存在实数,使()有最小值3,
①当时,在上单调递减,,(舍去),
②当时,在上单调递减,在上单调递增
,,满足条件.
③当时,在上单调递减,,(舍去),
综上,存在实数,使得当时有最小值3.
(III)令,由(2)知,.令,,
当时,,在上单调递增
∴ 即
21.(本题满分14分)在数列中,,其中.
(Ⅰ)求数列的通项公式;
(Ⅱ)求数列的前项和;
(Ⅲ)证明存在,使得对任意均成立.
解:(Ⅰ)解法一:, ,
.由此可猜想出数列的通项公式为.
以下用数学归纳法证明.
(1)当时,,等式成立.
(2)假设当时等式成立,即,
那么.
这就是说,当时等式也成立.根据(1)和(2)可知,等式对任何都成立.
解法二:由,,可得,
所以为等差数列,其公差为1,首项为0,故,所以数列的通项公式为.
(Ⅱ)解:设, ①
②
当时,①式减去②式,
得,
.
这时数列的前项和.
当时,.这时数列的前项和.
(Ⅲ)证明:通过分析,推测数列的第一项最大,下面证明:
. ③
由知,要使③式成立,只要,
因为
.
所以③式成立.
因此,存在,使得对任意均成立.
第4题
第8题
正视图
侧视图
俯视图
同课章节目录
