高一上学期周末练习(数学)(含前面的集合、函数知识)
文档属性
| 名称 | 高一上学期周末练习(数学)(含前面的集合、函数知识) |

|
|
| 格式 | zip | ||
| 文件大小 | 97.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-06 00:00:00 | ||
图片预览


文档简介
2011-2012学年高一上学期数学周末练习
命题人: 审题人: 班级 姓名 分数
一、选择题(5分*10=50分)
1.已知全集,则集合等于( ).
A. B. C. D.
2. 函数的定义域为( )
A. B.
C. D.
3. 如右图,正方体ABCD—A1B1C1D1中,E、F分别是
CC1、C1D1的中点,则异面直线EF和BD所成的角
的大小为 ( )
A.75° B.60°
C.45° D.30°
4. 与函数有相同的图像的函数是( )
A. B.
C. D.
5. 设有直线m、n和平面、.下列四个命题中,正确的是( )
A.若m∥,n∥,则m∥n
B.若m,n,m∥,n∥,则∥
C.若,m,则m
D.若,m,m,则m∥
6. 函数的零点个数为 ( )
A.0 B.1 C.2 D.3
7. 函数f(x) =x +a与y =logax图象只可能是下图中的( ).
8.三个函数①y=;②y=2-x;③y=-x3中,在其定义域内既是奇函数又是减函数的个数是
A.0 B.1 C.2 D.3
9. 设f(x)= 则不等式f(x)>2的解集为( )
A.(1,2)(3,+∞) B.(,+∞)
C.(1,2) ( ,+∞) D.(1,2)
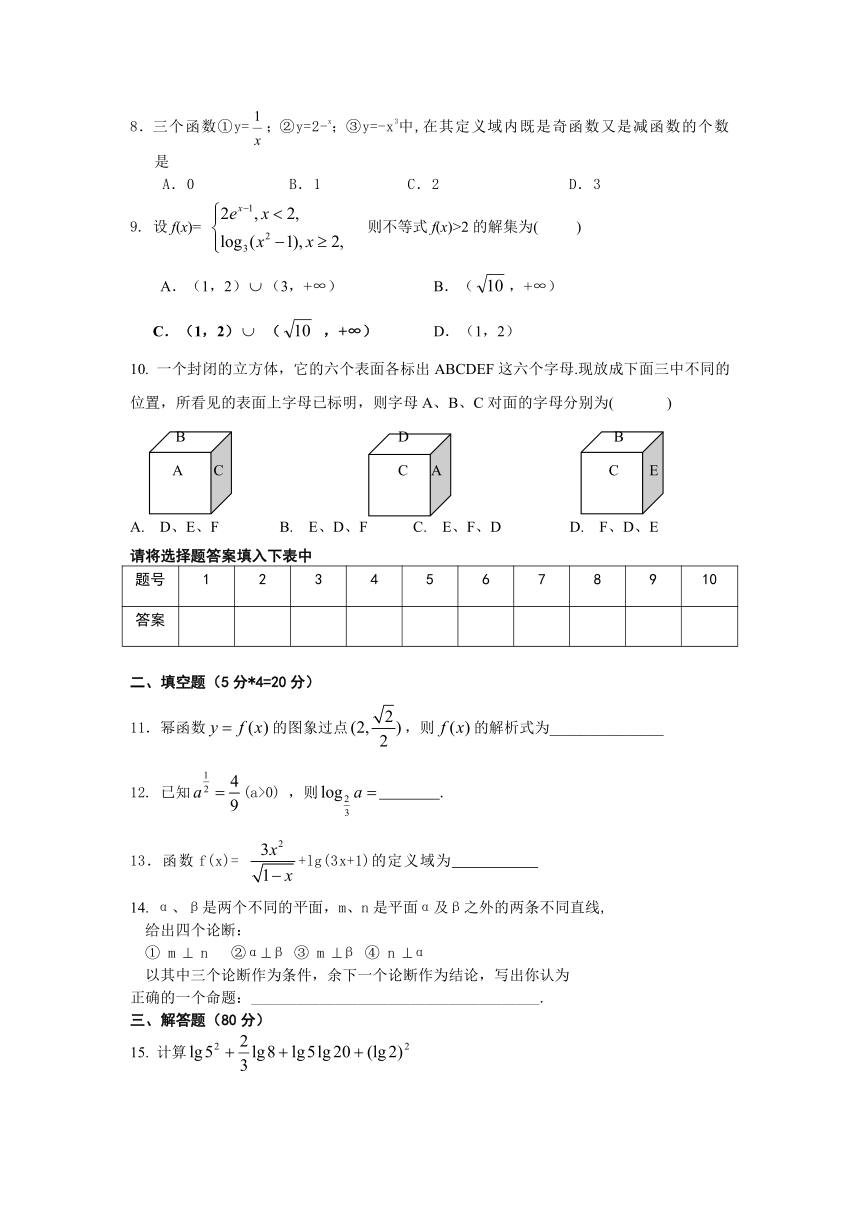
10. 一个封闭的立方体,它的六个表面各标出ABCDEF这六个字母.现放成下面三中不同的位置,所看见的表面上字母已标明,则字母A、B、C对面的字母分别为( )
B D B
A C C A C E
A. D、E、F B. E、D、F C. E、F、D D. F、D、E
请将选择题答案填入下表中
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题(5分*4=20分)
11.幂函数的图象过点,则的解析式为_______________
12. 已知(a>0) ,则 .
13.函数f(x)= HYPERLINK "http://www./" +lg(3x+1)的定义域为
14. α、β是两个不同的平面,m、n是平面α及β之外的两条不同直线,
给出四个论断:
① m n ②αβ ③ m β ④ n α
以其中三个论断作为条件,余下一个论断作为结论,写出你认为
正确的一个命题:______________________________________.
三、解答题(80分)
15. 计算
16. 用单调性的定义证明:函数f(x)= -x在区间(0,∞)上为减函数
17.已知函数
⑴求函数的定义域; ⑵判断函数的奇偶性,并予以证明;
⑶求使<0成立的的集合。
18、通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设表示学生注意力随时间(分钟)的变化规律(越大,表明学生注意力越大),经过实验分析得知:
,
(1)讲课开始后多少分钟,学生的注意力最集中?能坚持多少分钟?
(2)讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需的状态下讲授完这道题目?
19. 如图,在四棱锥中,底面ABCD是正方形,侧棱底面ABCD,,E是PC的中点,作交PB于点F。
(I)证明 平面;
(II)证明平面EFD;
(III)求二面角的大小。
20.已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且
(Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(Ⅱ)当λ为何值时,平面BEF⊥平面ACD? (14分)
平冈中学2011-2012学年高一上学期数学周末练习19
参考答案
选择题
1—5:CCBBD 6—10:BCACD
二、填空题
11、(3,0) 3 12、4 13、-1 14、②③④则①
三、解答题
15、3
函数f(x)= HYPERLINK "http://www./" -x在区间(0,∞)上为减函数
17、⑴由题意得:
所以所求定义域为
⑵令H
则H(
故为奇函数,
⑶
当
综上:
18解:(1)当时,是增函数,且。
当时,是减函数,且。
所以,讲课开始10分钟,学生的注意力最集中,能坚持10分钟。
(2),
所以,讲课开始后25分钟时,学生的注意力比讲课开始后5分钟更集中。
(3)当时,令,则。
当时,令,则。
所以,学生的注意力在180以上所持续的时间。
所以,经过适当安排,老师能在学生达到所需的状态下讲授完这道题目。
19 、(I)证明:连结AC,AC交BD于O。连结EO。
底面ABCD是正方形,点O是AC的中点
在中,EO是中位线,。
而平面EDB且平面EDB,
所以,平面EDB。
(II)证明:底在ABCD且底面ABCD,
① 同样由底面ABCD,得底面ABCD是正方形,有平面PDC
而平面PDC, ② ………………………………6分
由①和②推得平面PBC 而平面PBC,
又且,所以平面EFD
(III)解:由(II)知,,故是二面角的平面角
由(II)知, 设正方形ABCD的边长为,则
在中,
在中,
所以,二面角的大小为
20、证明:(Ⅰ)∵AB⊥平面BCD, ∴AB⊥CD,
∵CD⊥BC且AB∩BC=B, ∴CD⊥平面ABC. 3分
又
∴不论λ为何值,恒有EF∥CD,∴EF⊥平面ABC,EF平面BEF,
∴不论λ为何值恒有平面BEF⊥平面ABC. 6分
(Ⅱ)由(Ⅰ)知,BE⊥EF,又平面BEF⊥平面ACD,
∴BE⊥平面ACD,∴BE⊥AC. 9分
∵BC=CD=1,∠BCD=90°,∠ADB=60°,
∴ 11分
由AB2=AE·AC 得 13分
故当时,平面BEF⊥平面ACD.
命题人: 审题人: 班级 姓名 分数
一、选择题(5分*10=50分)
1.已知全集,则集合等于( ).
A. B. C. D.
2. 函数的定义域为( )
A. B.
C. D.
3. 如右图,正方体ABCD—A1B1C1D1中,E、F分别是
CC1、C1D1的中点,则异面直线EF和BD所成的角
的大小为 ( )
A.75° B.60°
C.45° D.30°
4. 与函数有相同的图像的函数是( )
A. B.
C. D.
5. 设有直线m、n和平面、.下列四个命题中,正确的是( )
A.若m∥,n∥,则m∥n
B.若m,n,m∥,n∥,则∥
C.若,m,则m
D.若,m,m,则m∥
6. 函数的零点个数为 ( )
A.0 B.1 C.2 D.3
7. 函数f(x) =x +a与y =logax图象只可能是下图中的( ).
8.三个函数①y=;②y=2-x;③y=-x3中,在其定义域内既是奇函数又是减函数的个数是
A.0 B.1 C.2 D.3
9. 设f(x)= 则不等式f(x)>2的解集为( )
A.(1,2)(3,+∞) B.(,+∞)
C.(1,2) ( ,+∞) D.(1,2)
10. 一个封闭的立方体,它的六个表面各标出ABCDEF这六个字母.现放成下面三中不同的位置,所看见的表面上字母已标明,则字母A、B、C对面的字母分别为( )
B D B
A C C A C E
A. D、E、F B. E、D、F C. E、F、D D. F、D、E
请将选择题答案填入下表中
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题(5分*4=20分)
11.幂函数的图象过点,则的解析式为_______________
12. 已知(a>0) ,则 .
13.函数f(x)= HYPERLINK "http://www./" +lg(3x+1)的定义域为
14. α、β是两个不同的平面,m、n是平面α及β之外的两条不同直线,
给出四个论断:
① m n ②αβ ③ m β ④ n α
以其中三个论断作为条件,余下一个论断作为结论,写出你认为
正确的一个命题:______________________________________.
三、解答题(80分)
15. 计算
16. 用单调性的定义证明:函数f(x)= -x在区间(0,∞)上为减函数
17.已知函数
⑴求函数的定义域; ⑵判断函数的奇偶性,并予以证明;
⑶求使<0成立的的集合。
18、通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设表示学生注意力随时间(分钟)的变化规律(越大,表明学生注意力越大),经过实验分析得知:
,
(1)讲课开始后多少分钟,学生的注意力最集中?能坚持多少分钟?
(2)讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需的状态下讲授完这道题目?
19. 如图,在四棱锥中,底面ABCD是正方形,侧棱底面ABCD,,E是PC的中点,作交PB于点F。
(I)证明 平面;
(II)证明平面EFD;
(III)求二面角的大小。
20.已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且
(Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(Ⅱ)当λ为何值时,平面BEF⊥平面ACD? (14分)
平冈中学2011-2012学年高一上学期数学周末练习19
参考答案
选择题
1—5:CCBBD 6—10:BCACD
二、填空题
11、(3,0) 3 12、4 13、-1 14、②③④则①
三、解答题
15、3
函数f(x)= HYPERLINK "http://www./" -x在区间(0,∞)上为减函数
17、⑴由题意得:
所以所求定义域为
⑵令H
则H(
故为奇函数,
⑶
当
综上:
18解:(1)当时,是增函数,且。
当时,是减函数,且。
所以,讲课开始10分钟,学生的注意力最集中,能坚持10分钟。
(2),
所以,讲课开始后25分钟时,学生的注意力比讲课开始后5分钟更集中。
(3)当时,令,则。
当时,令,则。
所以,学生的注意力在180以上所持续的时间。
所以,经过适当安排,老师能在学生达到所需的状态下讲授完这道题目。
19 、(I)证明:连结AC,AC交BD于O。连结EO。
底面ABCD是正方形,点O是AC的中点
在中,EO是中位线,。
而平面EDB且平面EDB,
所以,平面EDB。
(II)证明:底在ABCD且底面ABCD,
① 同样由底面ABCD,得底面ABCD是正方形,有平面PDC
而平面PDC, ② ………………………………6分
由①和②推得平面PBC 而平面PBC,
又且,所以平面EFD
(III)解:由(II)知,,故是二面角的平面角
由(II)知, 设正方形ABCD的边长为,则
在中,
在中,
所以,二面角的大小为
20、证明:(Ⅰ)∵AB⊥平面BCD, ∴AB⊥CD,
∵CD⊥BC且AB∩BC=B, ∴CD⊥平面ABC. 3分
又
∴不论λ为何值,恒有EF∥CD,∴EF⊥平面ABC,EF平面BEF,
∴不论λ为何值恒有平面BEF⊥平面ABC. 6分
(Ⅱ)由(Ⅰ)知,BE⊥EF,又平面BEF⊥平面ACD,
∴BE⊥平面ACD,∴BE⊥AC. 9分
∵BC=CD=1,∠BCD=90°,∠ADB=60°,
∴ 11分
由AB2=AE·AC 得 13分
故当时,平面BEF⊥平面ACD.
